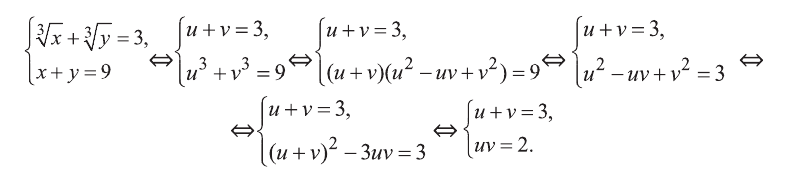Иррациональные уравнения

Системы

Что же делать в случаях, когда требуется осуществить решение систем иррациональных уравнений, и у нас в наличии не одно, а целых два неизвестных? Здесь поступаем так же, как в обычных случаях, но с учетом вышеперечисленных свойств данных математических выражений. И в каждой новой задаче, разумеется, следует применять творческий подход. Но, опять же, лучше рассмотреть все на конкретном примере, представленном ниже. Здесь не просто требуется найти переменные х и у, но и указать в ответе их сумму. Итак, имеется система, содержащая иррациональные величины (см. фото ниже).

Как можно убедиться, подобная задача не представляет ничего сверхъестественно сложного. Требуется лишь проявить сообразительность и догадаться, что левая часть первого уравнения представляет собой квадрат суммы. Подобные задания встречаются в ЕГЭ.

Неограниченное приближение

Природа иррационального наиболее ясно и полно может быть объяснена и познана только через нескончаемый ряд чисел десятичной дроби. А конкретным, ярким примером из членов этого семейства является πи. Не без оснований предполагается, что эта математическая константа была известна с древних времен, используясь при вычислении длин окружности и площади круга. Но среди европейцев ее впервые применили на практике англичанин Уильям Джонс и швейцарец Леонард Эйлер.

Возникает эта константа следующим образом. Если сравнивать самые разные по длине окружности, то отношение их длин и диаметров в обязательном порядке равны одному и тому же числу. Это и есть πи. Если выразить его через обыкновенную дробь, то приблизительно получим 22/7. Впервые это сделал великий Архимед, портрет которого представлен на рисунке выше. Именно поэтому подобное число получило его имя. Но это не явное, а приближенное значение едва ли не самого удивительного из чисел. Гениальный ученый с точностью до 0,02 нашел искомую величину, но, по сути, данная константа не имеет реального значения, а выражается как 3,1415926535… Она представляет собой бесконечный ряд цифр, неограниченно приближаясь к некоему мифическому значению.

Применение графического исследования к решению задач ЕГЭ уровня А[править]

Уметь строить эскизы левой и правой частей уравнения
ax+b=cx+d{\displaystyle {\sqrt {ax+b}}=cx+d}
очень полезно. Графическая интерпретация решения такого уравнения помогает быстро решить некоторые задачи ЕГЭ.

Пример 10.править

Какое утверждение
1) уравнение имеет два корня одного знака (оба корня или положительны, или оба корня отрицательны);
2) уравнение имеет только один корень, и он отрицателен;
3) уравнение имеет два корня разных знаков;
4) уравнение имеет только один корень, и он положителен
верно по отношению к корням уравнения

1. а)x+4=3(x+1){\displaystyle {\sqrt {x+4}}=3\left({x+1}\right)};
2. б)7−x=x+1{\displaystyle {\sqrt {7-x}}=x+1};
3. в)310−x=12−x{\displaystyle 3{\sqrt {10-x}}=12-x};
4. г)57−x=13−x{\displaystyle 5{\sqrt {7-x}}=13-x} ?

Для ответа на поставленный вопрос не обязательно решать уравнение. Часто достаточно аккуратно начертить эскизы левой и правой частей.

а) x+4=3(x+1).{\displaystyle {\sqrt {x+4}}=3\left({x+1}\right).}

Рис. 3

На чертеже надо отметить точки пересечений полупараболы и прямой с осями координат. Из рисунка ясно, что пересечение происходит на отрицательной полуоси — это обеспечивается тем, что прямая пересекает ось Ox правее полупараболы, а ось Oy выше полупараболы.

Ответ: 2).

б) 7−x=x+1.{\displaystyle {\sqrt {7-x}}=x+1.}

Рис. 4

Из рисунка (рис. 4) ясно, что пересечение происходит на положительной полуоси.
Это обеспечивается тем, что прямая пересекает отрицательную полуось Ox, а ось Oy прямая пересекает ниже полупараболы.

Ответ: 4).

в)310−x=12−x.{\displaystyle 3{\sqrt {10-x}}=12-x.}

Рис. 5

Это более трудный пример, так как не ясно, прямая пересекается с полупараболой (а тогда дважды), касается или вовсе не имеет общих точек с полупараболой. Надо что-то сделать дополнительно, например, подставить такие значения х, при которых корни извлекаются нацело, или поискать точку (x = 5), в которой ясно, что расположено выше — прямая или полупарабола.

Ответ: 1).

г)57−x=13−x?{\displaystyle 5{\sqrt {7-x}}=13-x?}

Рис. 6

Из рисунка ясно, что корней два, и они разных знаков. Это обеспечивается тем, что прямая пересекает ось Ox правее, а ось Oy ниже полупараболы.

Ответ: 3).

Лекция по математике. Тема: «Иррациональные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Изучение нового материала

Изучение нового материала

Иррациональным называется уравнение, в котором неизвестное (переменная) содержится под знаком корня или под знаком операции возведения в рациональную (дробную) степень.

Для решения иррациональных уравнений обычно используются следующие приемы:

1)возведение в соответствующую степень обе части уравнения;

2) введение новой переменной;

3) сведение к системе уравнений;

4) применение свойств функций, входящих в уравнение.

При решении иррациональных уравнений необходима проверка всех найденных корней путем их подстановки в исходное уравнение или нахождение ОДЗ и следующий анализ корней (при решении методом приведения к равносильной смешанной системе уравнений и неравенств необходимость в этом отпадает).

Простейшим иррациональным уравнением является уравнение вида:

при решении которого важную роль играет четность или нечетность n .

Если n — нечетное, то данное уравнение равносильно уравнению

Если n — четное, то, так как корень считается арифметическим, необходимо учитывать ОДЗ (область допустимых значений):

Решение . Так как n =2 — четное, то обе части уравнения возводим во 2ю степень:

Решить уравнение

Решение. Так как в данном примере n =3 — нечетное, то после возведения обеих частей уравнения в третью степень получим равносильное данному уравнение:

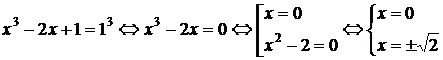
Ответ:

Решить уравнение

Решение . Так как n =2 — четное, то исходное уравнение равносильно системе:

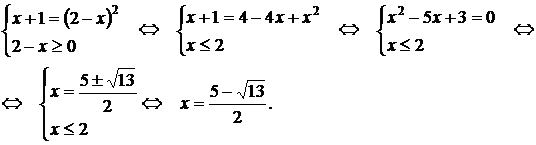
Ответ:

Уравнения вида

n — четное

Р ешить уравнение :

Р ешить уравнение:

Решение. Запишем данное уравнение в виде: Возводя обе части в квадрат и учитывая, что получим уравнение 2х+6=х+1 , решение которого есть х = -5 – не удовлетворяет выписанному условию. Значит, данное уравнение не имеет решений.

Ответ: нет решений

Если иррациональное уравнение содержит несколько радикалов. В этом случае для избавления от радикалов уравнение приходится возводить в соответствующую степень несколько раз. При этом предварительно уединяют один из радикалов так, чтобы обе части уравнения стали неотрицательными

Особое внимание следует обратить на правильное нахождение ОДЗ

Решить уравнение

Решение. Запишем уравнение в виде:

Полученное уравнение равносильно исходному . Для его решения рассмотрим систему:

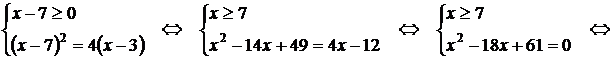
Ответ:

 Введение новой переменной в ряде случаев позволяет перейти от иррационального уравнения к рациональному уравнению.

Решить уравнение

Решение. Возведение данного уравнения в квадрат привело бы к уравнению четвертой степени, что нерационально. Поэтому запишем уравнение в виде

Получим

Вернемся к «старым» переменным

Ответ:

 Иногда при решении иррационального уравнения возникает необходимость ввести не одну, а несколько «новых» переменных. Такая ситуация возникает, например, при решении уравнений, содержащих радикалы разных степеней.

Решить уравнение

Решение. Пусть

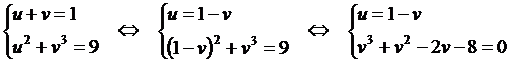
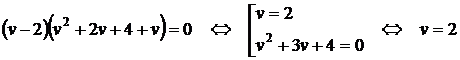
Получим, что

Ответ: нет решений.

 При решении некоторых иррациональных уравнений нахождение области допустимых значений входящих в уравнение неизвестных может существенно облегчить решение уравнения.

Решить уравнение

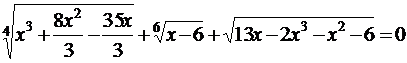
Решение. Данное уравнение имеет весьма громоздкий вид и неясно как подойти к его решению. Поэтому найдем сначала ОДЗ:

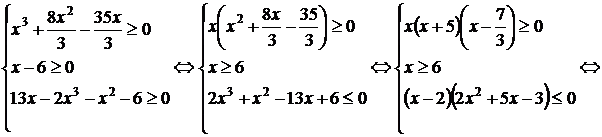
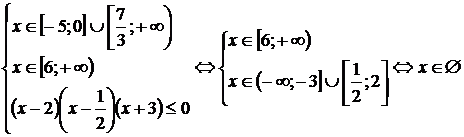
Получим, что область допустимых значений данного уравнения является пустым множеством и, следовательно, данное уравнение решений не имеет.

Ответ: нет решений.

При решении иррациональных уравнений бывает полезно воспользоваться монотонностью функций.

Решить уравнение

Решение. Один корень данного уравнения

По свойству степенных функций функции

Ответ:

Что такое параметр

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно \(\frac{20}{5} = 4\). А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная «a»  называется параметр. 

Параметр —  коэффициент при неизвестном или свободном члене. Параметр задается буквой, но является не переменной, а числом, которое мы не знаем.

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Игра в прятки: как значение одной переменной может помочь найти другую?Представьте, что вы играете в прятки и не знаете, кого ищете. Параметр a пусть будет местоположением прячущегося игрока x. Когда вы найдете значение параметра a, то есть место, где прячется игрок, тогда вы сможете найти и самого игрока и понять, кого нашли — нашли значение переменной x. Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.

Мы разобрались с тем, что такое параметр и с чем его едят. Теперь научимся применять новые знания для решения линейных уравнений.

Избавление от иррационального

Иррациональные уравнения и неравенства могут включать в себя переменную не только под знаком квадратного корня. Он может быть любой степени. Самым распространенным способом от него избавиться является возможность возвести обе части равенства в соответствующую степень. Это основное действие, помогающее при операциях с иррациональным. Действия в четных случаях особенно не отличаются от тех, которые были уже разобраны нами ранее. Здесь должны быть учтены условия неотрицательности подкоренного выражения, а также по окончании решения необходимо производить отсев посторонних значений переменных таким образом, как было показано в рассмотренных уже примерах.

Из дополнительных преобразований, помогающих найти правильный ответ, часто используется умножение выражения на сопряженное, а также нередко требуется введение новой переменной, что облегчает решение. В некоторых случаях, чтобы отыскать значение неизвестных, целесообразно применять графики.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию

Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Иррациональные уравнения

Мы уже рассмотрели два вида рациональных уравнений, перейдем к иррациональным.

Иррациональное уравнение – это уравнение, которое содержит неизвестную под корнем или она возведена в дробную степень.

Например: \(\sqrt{10 — x} = x — 4; x^{\frac{2}{3}} = 4\)  – это иррациональные уравнения.

Иррациональные уравнения могут быть нескольких видов:

1. \(\sqrt{f(x)} = g(x)\)
2. \(\sqrt{f(x)} = \sqrt{g(x)}\)
3. Разные комбинации корней.

Чудо метод: как легко решить любое иррациональное уравнение?Такие уравнения решаются методом возведения в квадрат. Он заключается в изоляции корня с одной стороны от знака равенства и переноса остальных слагаемых в другую сторону, далее нужно возвести обе части уравнения (и правую, и левую) в квадрат, чтобы избавиться от знака корня. Такой метод можно использовать столько раз, сколько потребуется, чтобы избавиться от всех корней в уравнении.

Что нужно учитывать при решении иррационального уравнения методом возведения в квадрат?

Корень не может быть отрицательным, поэтому обязательно нужно добавлять условие на выражение, к которому приравнивается корень. Такое выражение всегда больше или равно нулю.

Алгоритм решения иррационального уравнения:

1. Поместить выражение с корнем в одну часть уравнения, а все остальное в другую.
2. Возвести в нужную степень обе части уравнения. 
3. Первые два пункта можно повторять, пока не избавитесь от всех корней.
4. Решить рациональное уравнение.

А теперь практика.

Решение уравнения вида \(\sqrt{f(x)} = g(x)\):

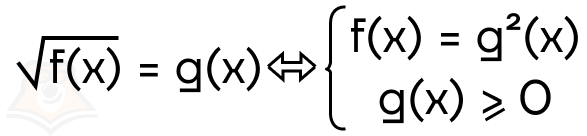
Пример:  

\(\large\sqrt{x^{2} — 5} = x + 1\)

1. Перейдем к системе

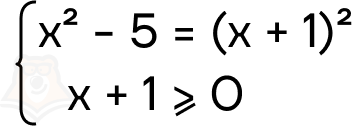
2. Решим первое уравнение и получим x = -3, но данный х не подходит под второе условие, поэтому уравнение не имеет корней.

Решение уравнения вида \(\sqrt{f(x)} = \sqrt{g(x)}\):

Пример: 

\(\large\sqrt{x^{2} + 2} = \sqrt{2x + 2}\)

1. Перейдем к системе 

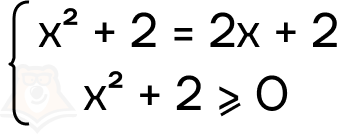
2. Заметим, что второе условие выполняется при любом х, а значит все корни первого уравнения будут являться решениями. Решим неполное квадратное уравнение, и получим корни 0 и 2.

Решение уравнения с тремя корнями:

Пример: 

\(\large\sqrt{1 + x} — \sqrt{1 — x} = \sqrt{x}\)

1. Найдем область допустимых значений (ОДЗ), то есть все значения, которые x может принимать в уравнении или неравенстве.

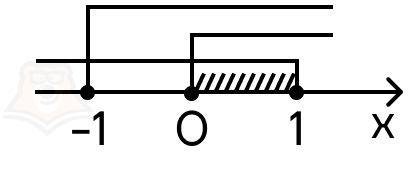
\(\Large 0 \leq x \leq 1\)

Без каких трёх букв не справиться с ЕГЭ?Таким тремя буквами является аббревиатура ОДЗ. В базовом ЕГЭ и первой части профильной математики можно обойтись и без ОДЗ. Но решить некоторые задания второй части профиля без ОДЗ не получится.Чтобы получить верный ответ последним действием нужно пересечь ОДЗ уравнения с его решениями. Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ.

2. Перенесем одно слагаемое в правую часть

\(\large\sqrt{1 + x} = \sqrt{x} + \sqrt{1 — x}\)

3. Возведем обе части уравнения в квадрат

\(\large 1 + x = x + 2 ⋅ \sqrt{x — 1} ⋅ \sqrt{x} + 1 — x\)

4. Сложим подобные слагаемые и получим систему вида fx=gx

\(\large x = 2\sqrt{1 — x}\sqrt{x}\)

5. Перейдем к системе уравнений

6. Решим первое уравнение 

x2 = 4x * (1 — x)5×2 — 4x = 0x * (5x — 4) = 0

Оба корня подходят и под условие x ≥ 0, и под найденное ранее ОДЗ, значит корни данного уравнения 0 и \(\large\frac{4}{5}\) .

Условия на корни квадратного трехчлена

Могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

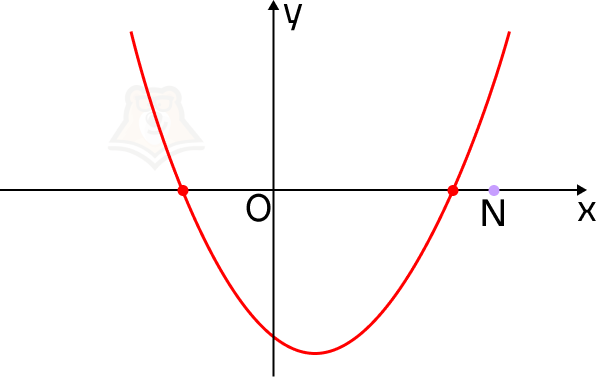
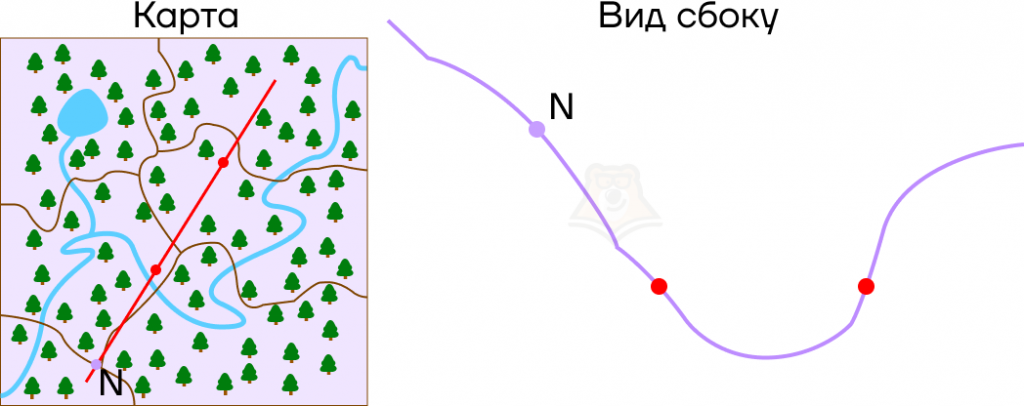
Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

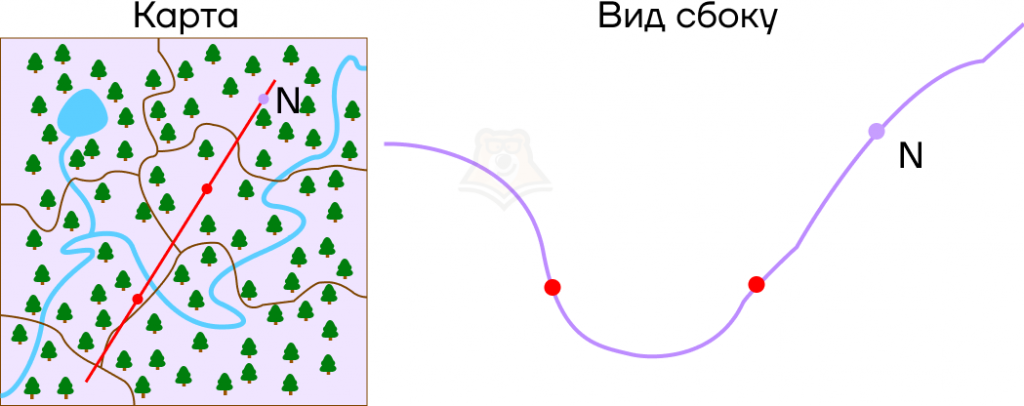
Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

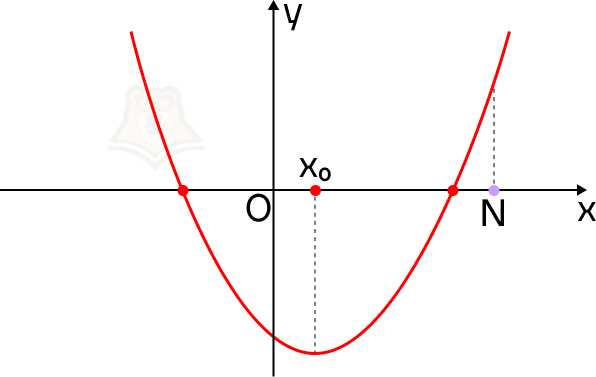
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

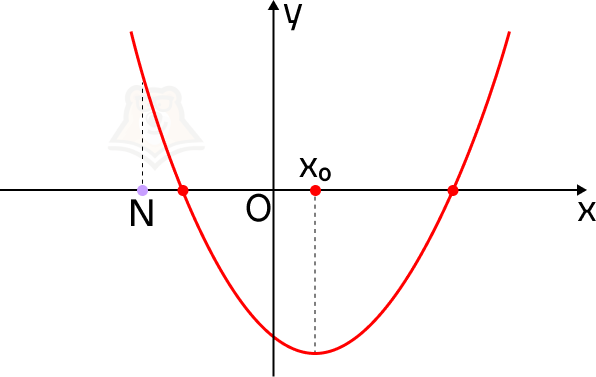
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

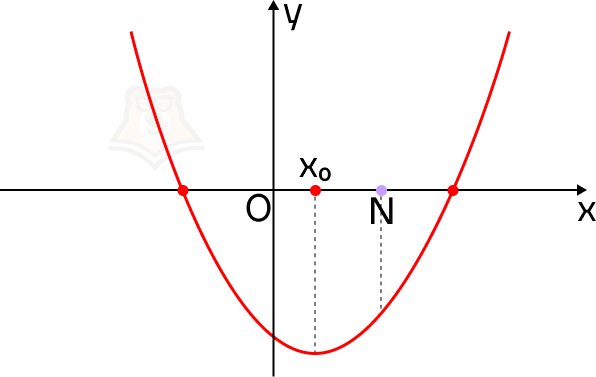
В этом случае смотровая площадка окажется между привалами. 

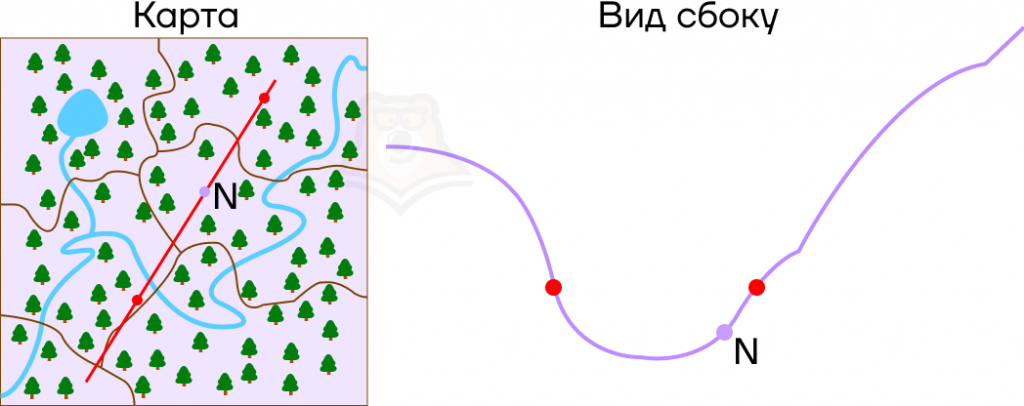
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

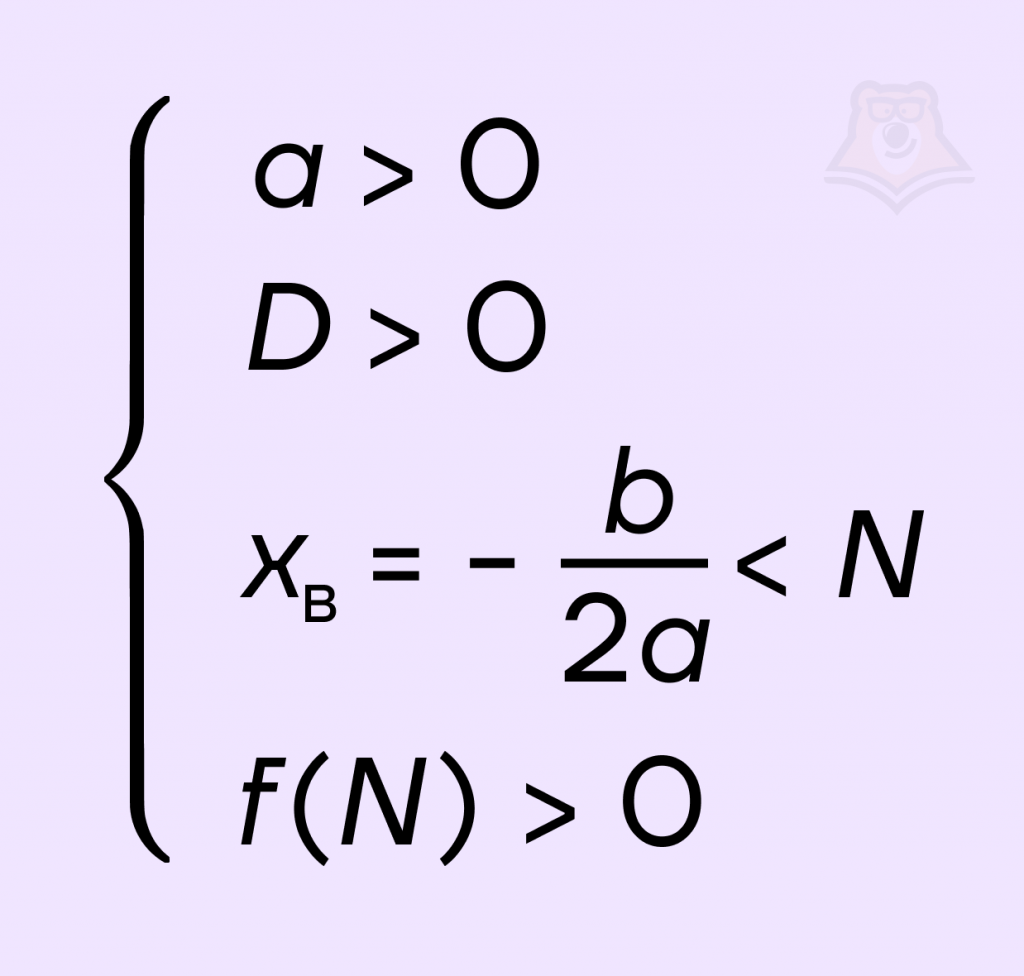
Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

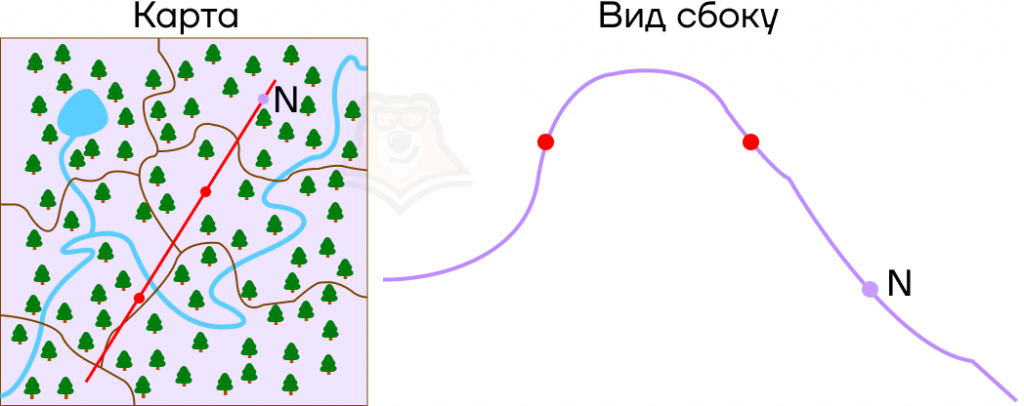
Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

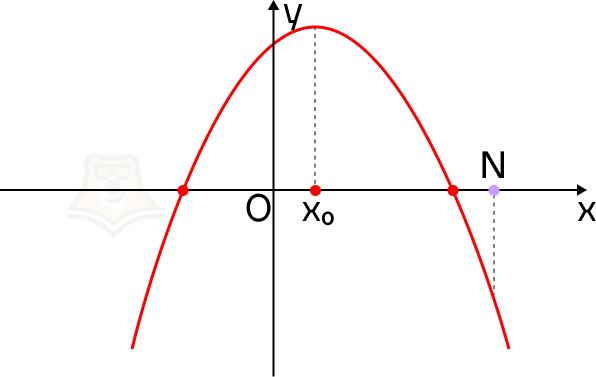
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

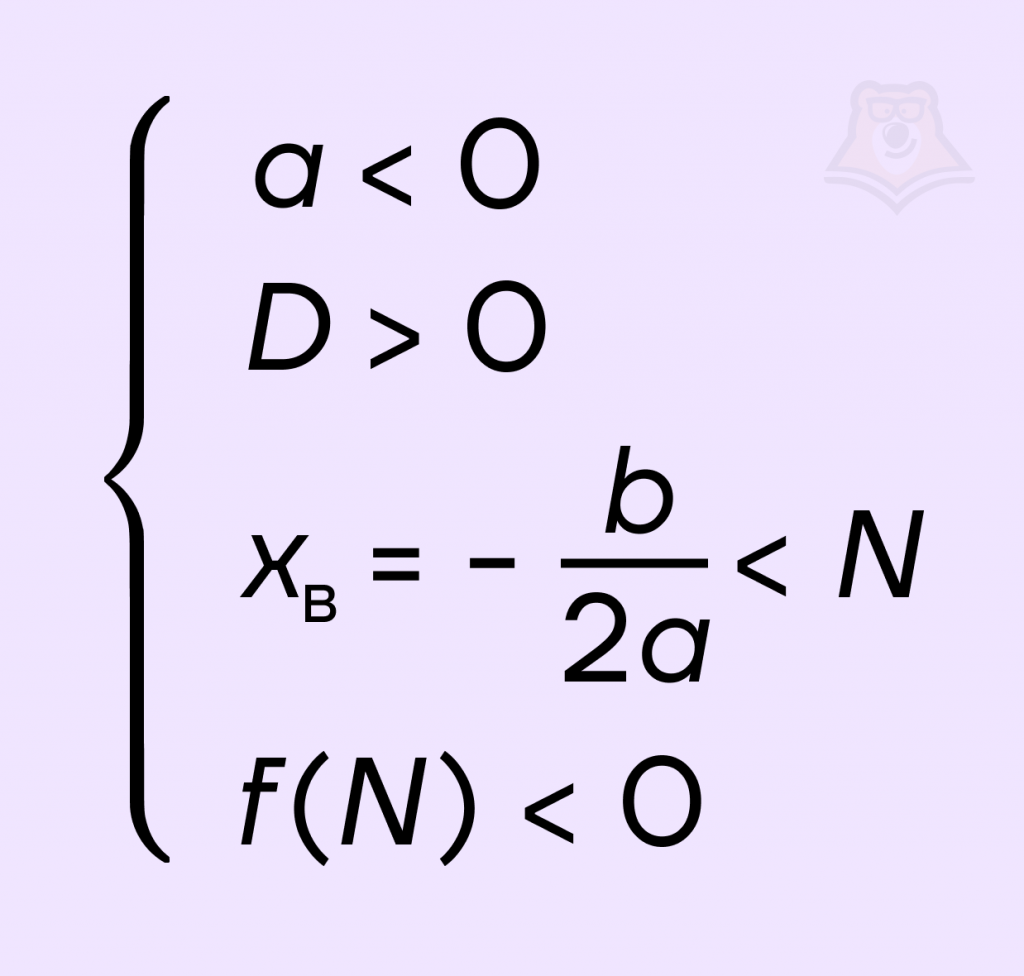
2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

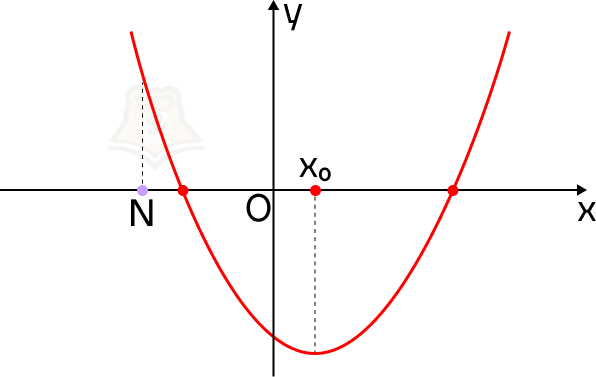
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

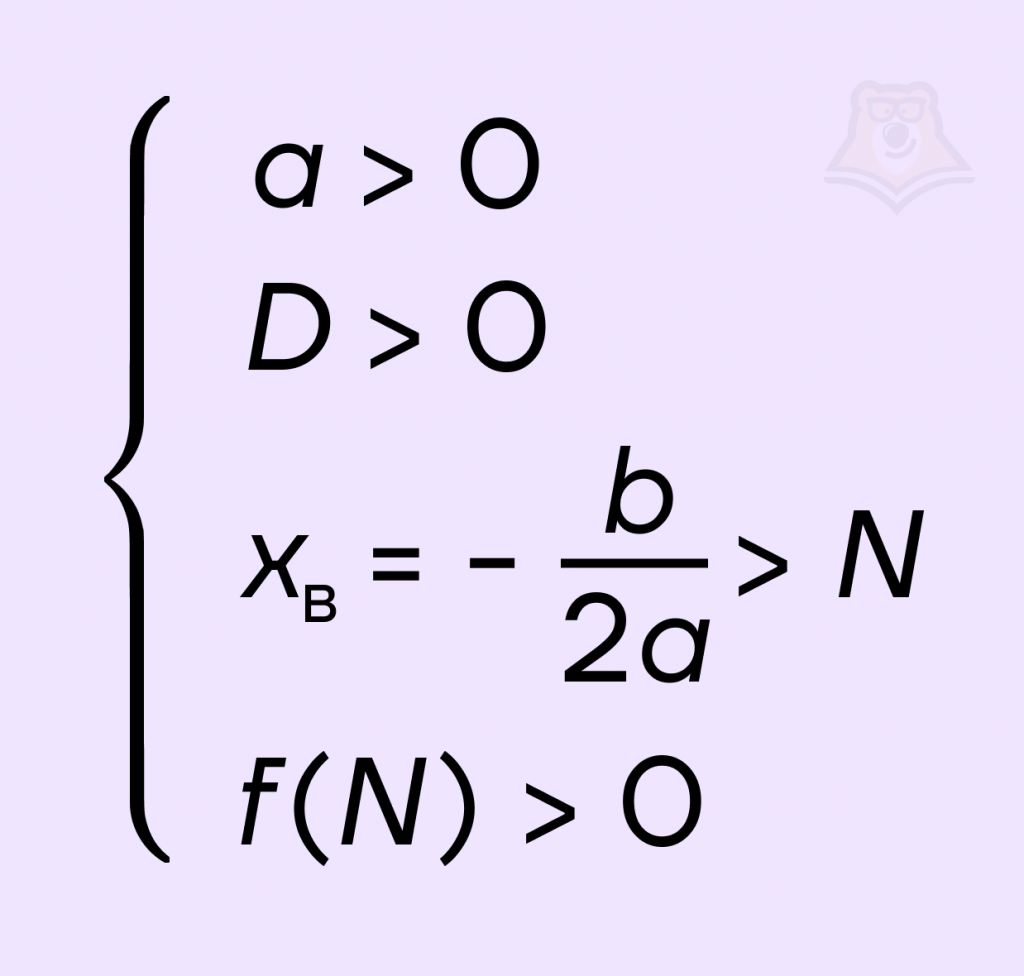
Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

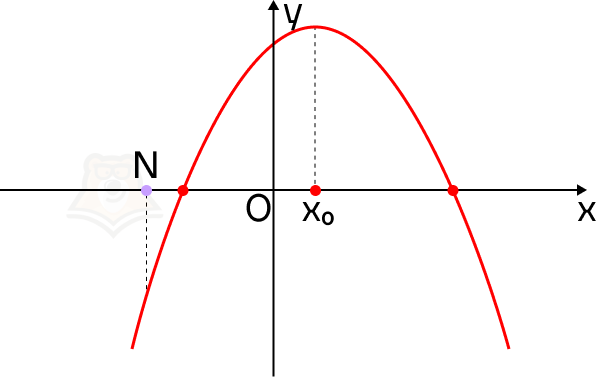
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

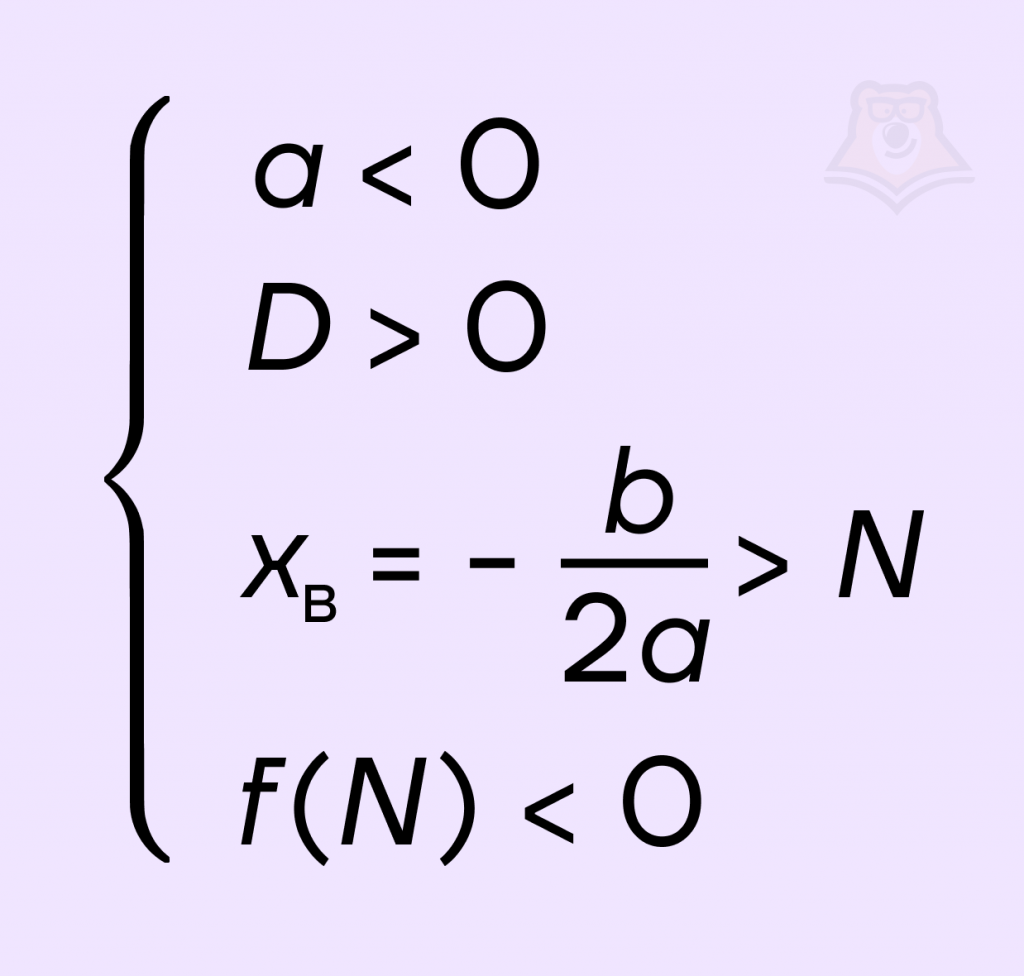
С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

Алгоритм: как задать любые условия для корней квадратных уравнений с помощью графика? Достаточно начертить примерный график функции и расставить на оси х нужные точки. Чтобы составить систему, необходимо: 1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2.2. Определить, сколько корней имеет уравнение и задать условие для дискриминанта.3. Определить расположение вершины параболы относительно точек на графике и задать условие для их абсцисс.4. Определить, какое значение принимает функция в данных точках относительно корней уравнения.

В итоге должна получиться система, с помощью которой можно решить задачу.

Это все, конечно, здорово, но как быть с иррациональными уравнениями?

Уравнения вида ax+b=cx+d.{\displaystyle {\sqrt {ax+b}}=cx+d.}[править]

Рассмотрим подробнее самое простое из уравнений вида
f(x)=g(x){\displaystyle {\sqrt {f\left(x\right)}}=g\left(x\right)}
— уравнение
ax+b=cx+d(1).{\displaystyle {\sqrt {ax+b}}=cx+d\quad (1).}

Мы предполагаем, что a≠{\displaystyle a\neq 0.}

Его можно решать различными способами.

Приведем три из них.

1. Можно воспользоваться приведенным выше условием равносильности:

ax+b=cx+d⇔{cx+d≥ax+b=(cx+d)2.{\displaystyle {\sqrt {ax+b}}=cx+d\Leftrightarrow \left\{{\begin{matrix}cx+d\geq 0\\ax+b=\left({cx+d}\right)^{2}.\\\end{matrix}}\right.}

2. Можно сразу решить уравнение
ax+b=(cx+d)2{\displaystyle ax+b=\left({cx+d}\right)^{2}}
(ОДЗ уравнения выполняется автоматически), а затем сделать проверку: подставить найденные решения в заданное уравнение
ax+b=cx+d.{\displaystyle {\sqrt {ax+b}}=cx+d.}

Обязательна ли проверка? Да, надо отсечь решения уравнения
−ax+b=cx+d.{\displaystyle -{\sqrt {ax+b}}=cx+d.}

Рассмотрим решения уравнения на графике.
Начертим эскизы левой и правой частей — например, рис. 1.

Рис. 1

В данном случае хорошо видно (рис. 1), что полупарабола
y=ax+b{\displaystyle y={\sqrt {ax+b}}}
пересекается лишь с той частью прямой
y=cx+d,{\displaystyle y=cx+d,}
где
y
принимает неотрицательные значения, а та часть прямой
y=cx+d,{\displaystyle y=cx+d,}
где
y
принимает отрицательные значения, пересекается с полупараболой
y=−ax+b,a>,b>{\displaystyle y=-{\sqrt {ax+b}},a>0,b>0.}

Рис. 2

Но «лишние» корни могут и не появиться (рис. 2) — все зависит от коэффициентов в уравнении, а, значит, от взаимного расположения прямой и полупараболы.

3. Уравнение вида
ax+b=cx+d{\displaystyle {\sqrt {ax+b}}=cx+d}
можно также решать с помощью замены переменных, положив
t=ax+b,t≥{\displaystyle t={\sqrt {ax+b}},t\geq 0.}
Тогда
ax+b=t2,{\displaystyle ax+b=t^{2},} откуда
x=t2−ba{\displaystyle x={\frac {t^{2}-b}{a}}}
и уравнение (1) в новых переменных примет вид
t=c(t2−b)a+d{\displaystyle t={\frac {c\left({t^{2}-b}\right)}{a}}+d}, что равносильно уравнению ct2−at−bc+ad={\displaystyle ct^{2}-at-bc+ad=0.}

Задача свелась к нахождению неотрицательных решений квадратного уравнения
ct2−at−bc+ad=,{\displaystyle ct^{2}-at-bc+ad=0,} что под силу любому школьнику.

Пример 7. (МФТИ, 2000)править

Найти все значения параметра
a,
при каждом из которых уравнение
x−8=−ax+3a+2{\displaystyle {\sqrt {x-8}}=-ax+3a+2}
имеет единственное решение.

Решим задачу третьим способом. Пусть
x−8=t,t≥,{\displaystyle {\sqrt {x-8}}=t,\;t\geq 0,}
тогда
x=t2+8{\displaystyle x=t^{2}+8}
и исходное уравнение примет вид
at2+t+5a−2={\displaystyle at^{2}+t+5a-2=0.}
Теперь задача состоит в том, чтобы найти все
a{\displaystyle a}, при которых уравнение
at2+t+5a−2={\displaystyle at^{2}+t+5a-2=0}
имеет единственное неотрицательное решение. Это имеет место в следующих случаях:

1. a=,{\displaystyle a=0,} и тогда t=2.{\displaystyle t=2.}
2. a≠,D≡1−20a2+8a=⇔{\displaystyle a\neq 0,D\equiv 1-20a^{2}+8a=0\Leftrightarrow }

a=−110⇒t=5a=12⇒t=−1⇒{\displaystyle \left[{\begin{matrix}a=-{\frac {1}{10}}\Rightarrow t=5\\a={\frac {1}{2}}\Rightarrow t=-1\\\end{matrix}}\right.\Rightarrow }
одно неотрицательное решение при
a=−110.{\displaystyle a=-{\frac {1}{10}}.}

3. a≠,D>⇔a∈(−110;12)⇔{\displaystyle a\neq 0,D>0\Leftrightarrow a\in \left({-{\frac {1}{10}}};{\frac {1}{2}}\right)\Leftrightarrow }
t1t2=5a−2a≤⇔a∈(;25⇒{\displaystyle t_{1}t_{2}={\frac {5a-2}{a}}\leq 0\Leftrightarrow a\in \left({0;{\frac {2}{5}}}\right]\Rightarrow }
имеем единственное неотрицательное решение при
a∈(;25.{\displaystyle a\in \left({0;{\frac {2}{5}}}\right].}

Итак, получаем

Ответ:
{−110}∪;25.{\displaystyle \left\{{-{\frac {1}{10}}}\right\}\cup \left.}

Уединение квадратного корня

Иррациональные уравнения вида \(\sqrt{f(x)}+q(x)=g(x)\)

Рассмотрим уравнения, в которых помимо квадратного корня в левой части есть еще другие слагаемые. Общий вид такого уравнения:
$$\sqrt{f(x)}+q(x)=g(x);$$
Тут уже так просто левую часть уравнения в квадрат не возведешь:
$$\left(\sqrt{f(x)}+q(x)\right)^2=$$
$$=\left(\sqrt{f(x)}\right)^2+2*\sqrt{f(x)}*q(x)+q^2(x)=$$
$$=f(x)+2*\sqrt{f(x)}*q(x)+q^2(x);$$
Как видите, от корня мы не избавились, смысла возводить в квадрат нет.

Но проблема легко решается переносом всех лишних слагаемых в исходном уравнении из левой части в правую так, чтобы в левой части остался только корень и больше ничего:
$$\sqrt{f(x)}=g(x)-q(x);$$
Теперь можно возводить в квадрат и решать аналогично примерам №4,5:
$$\begin{cases}
\left(\sqrt{f(x)}\right)^2=(g(x)-q(x))^2, \\
g(x)-q(x) \geq 0;
\end{cases}
$$
$$\Downarrow$$
$$
\begin{cases}
f(x)=(g(x)-q(x))^2, \\
g(x)-q(x) \geq 0;
\end{cases} $$

Рассмотрим на примере:

Возведение в квадрат

Но вернемся к иррациональным уравнениям. Чтобы отыскать неизвестное, в данном случае очень часто прибегают к простому методу: возводят обе части имеющегося равенства в квадрат. Подобный способ обычно дает хорошие результаты. Но следует учитывать коварство иррациональных величин. Все полученные в результате этого корни необходимо проверять, ведь они могут не подойти.

Но продолжим рассмотрение примеров и постараемся найти переменные вновь предложенным способом.

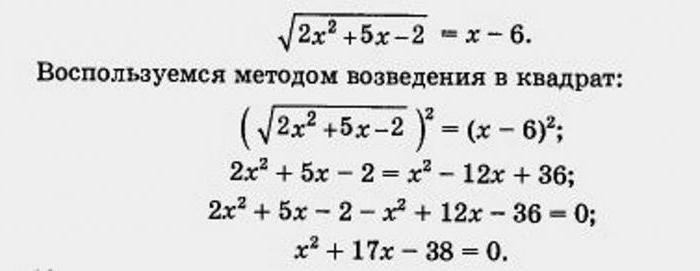
Совсем несложно, применив теорему Виета, найти искомые значения величин после того, как в результате определенных оперций у нас образовалось квадратное уравнение. Здесь получается, что среди корней будут 2 и -19. Однако при проверке, подставив полученные значение в изначальное выражение, можно убедиться, что ни один из этих корней не подходит. Это частое явление в иррациональных уравнениях. Значит, наша дилемма вновь не имеет решений, а в ответе следует указать пустое множество.

Иррациональное в математике

Каждый раз потребность в создании новых видов чисел возникала у человечества тогда, когда ему не хватало «простора» для решения каких-то уравнений. Иррациональные числа не являются исключением

Как свидетельствуют факты из истории, впервые великие мудрецы обратили на это внимание еще до нашей эры, веке в VII. Сделал это математик из Индии, известный под именем Манава

Он отчетливо понимал, что из некоторых натуральных чисел невозможно извлечь корень. К примеру, к таковым относятся 2; 17 или 61, а также многие другие.

Один из пифагорейцев, мыслитель по имени Гиппас, пришел к тому же выводу, пытаясь производить вычисления с числовыми выражениями сторон пентаграммы. Открыв математические элементы, которые не могут быть выражены цифровыми значениями и не обладают свойствами обычных чисел, он настолько разозлил своих коллег, что был выброшен за борт корабля, в море. Дело в том, что другие пифагорейцы сочли его рассуждения бунтом против законов вселенной.

Еще 2 подковырки иррациональных уравнений

Теперь пришло время перестать считать и немножко включить воображение. Оно может помочь не только на литературе, но и в математике.

Расслабьтесь с ОДЗ

Надеюсь, что я достаточно настращал вас ужасными несуществующими корнями (которые проникают в личное пространство корня и делают его отрицательным). Теперь ОДЗ наконец станет вашим другом?

Но все-таки бывают случаи, когда ОДЗ можно не выписывать. Это такие примеры, где выражение будет неотрицательным при любом значении переменных. Какой бы х вы не подставили – все равно выражение останется положительным или равным нулю.

 Разберем на примере.

в данных примерах нет смысла записывать ОДЗ: функции 1) (x2 + 6) 2) (x2 + x + 6)  — всегда положительны.

В случае 1. Квадрат + положительное число (попробуйте подставить хоть даже -120 миллионов – все равно ответ будет положительным).

В случае 2. Отрицательный дискриминант. Дискриминант говорит нам, что график этой квадратичной функции – парабола, которая существует, только над осью Ох: значит, вообще не принимает отрицательные значения.

(Если вы не в курсе, почему отрицательный дискриминант стал причиной приведенных рассуждений – читайте статью «6 простых трюков как решить квадратное уравнение ». В ней все доходчиво написано, да еще и узнаете пару способов быстрого решения квадратного уравнения).

Вы поняли: можно сначала окинуть взором подкоренное выражение – мало ли оно всегда неотрицательное. Вам меньше трудов – ОДЗ не надо писать.

Уже попадались уравнения, которые НЕ стоит решать возведением? О них далее…

Системы иррациональных уравнений

Решение систем, состоящих из иррациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует учитывать области существования участвующих иррациональных выражений.

Пример:

Решите систему уравнений

Решение:

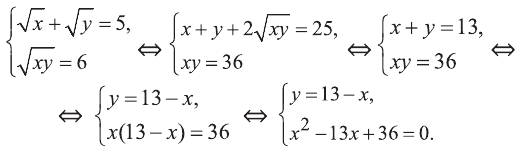
Данная система имеет решения 

Пример:

Решите систему уравнений

Решение:

 Обозначим Воспользовавшись формулой сокращенного умножения, получим систему: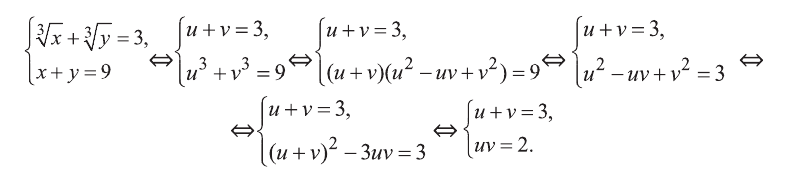

Эта система имеет решения Отсюда получим решения (1; и (8; 1) исходной системы.

Пример:

Найдите точку С(х; 0), равноудаленную от точек А(3; 4) и В(-2; 5) плоскости.

Решение:

Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение

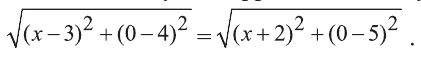
Делая равносильные преобразования, получим уравнение, откуда -10х=4. Последнее уравнение имеет корень х=-0,4. Значит, С(-0,4; 0) — искомая точка.

Пример:

Найдите точку на прямой у=3х, равноудаленную от точек А(-1;2) и В(3;—4) плоскости.

Решение:

По условию, ордината и абсцисса искомой точки удовлетворяет соотношению у=3х, поэтому она имеет координаты С(х;3х). Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение Делая равносильные преобразования, получим уравнение, откуда -28х=20. Последнее уравнение имеет корень

Значит, С(—5/7; -15/7) — искомая точка. Ответ: С(-5/7; -15/7). 

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – .

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем

Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа

Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то ) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

x– 5 = 62

х = 36 + 5

х = 41

Ответ: 41.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

х – 5 = (– 6)3

х = – 216 + 5

х = – 211

Ответ: – 211.

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х2 – 14х = 25

х2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью :

D = b2– 4ac = (– 14)2 – 4•1•(– 32) = 196 + 128 = 324

х₁ = (14 – 18)/2 = – 2

х₂ = (14 + 18)/2 = 16

Итак, нашли два корня: (– 2) и 16.

Ответ: (– 2); 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = (х – 4)2

х – 2 = х2 – 8х + 16

х2 – 9х + 18 = 0

D = b2– 4ac = (– 9)2 – 4•1•18 = 81 – 72 = 9

х₁ = (9 – 3)/2 = 3

х₂ = (9 + 3)/2 = 6

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3     х – 4 = 3 – 4 = – 1

при х = 6     6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Ответ: 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х2 + 6х – 25 = (1 – х)3

3х2 + 6х – 25 = 1 – 3х + 3х2 – х3

х3 + 9х – 26 = 0

Получили кубическое ур-ние. Решить его можно . Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

23 + 9•2 – 26 = 0

8 + 18 – 26 = 0

0 = 0

Других корней нет. Это следует из того факта, что функция у = х3 + 9х – 26 является .

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2   1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Ответ: 2.