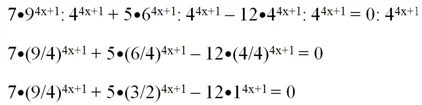Показательные уравнения и методы решения показательных уравнений

Уравнения с заменой переменных

В ряде случаев для решения показательного уравнения следует ввести новую переменную. В учебных заданиях такая замена чаще всего (но не всегда) приводит к квадратному ур-нию.

Задание. Решите уравнение методом замены переменной

Заметим, что в уравнении стоят степени тройки и девятки, но 32 = 9. Тогда введем новую переменную t = 3x. Если возвести ее в квадрат, то получим, что

C учетом этого изначальное ур-ние можно переписать:

Получили обычное квадратное ур-ние. Решим его:

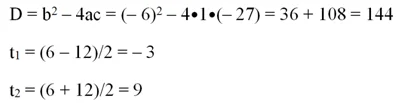
Мы нашли два значения t. Далее необходимо вернуться к прежней переменной, то есть к х:

Первое ур-ние не имеет решений, ведь показательная функция может принимать лишь положительные значения. Поэтому остается рассмотреть только второе ур-ние:

Ответ: 2.

Задание. Найдите корни ур-ния

Решение. Здесь в одном ур-нии стоит сразу три показательных функции. Попытаемся упростить ситуацию и избавиться от одной из них. Для этого поделим ур-ние на выражение 44х+1:

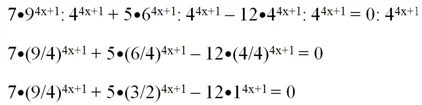
Так как 14х+1 = 1, мы можем записать:

Обратим внимание, что делить ур-ние на выражение с переменной можно лишь в том случае, если мы уверены, что оно не обращается в ноль ни при каких значениях х. В данном случае мы действительно можем быть в этом уверены, ведь величина 44х+1 строго положительна при любом х

Вернемся к ур-нию. В нем стоят величины (9/4)4х+1 и (3/2)4х+1. У них одинаковые показатели, но разные степени. Однако можно заметить, что

9/4 = (3/2)2, поэтому и (9/4)4х+1 = ((3/2)4х+1)2. Это значит, что перед нами уравнение с заменой переменных.

Произведем замену t = (3/2)4х+1, тогда (9/4)4х+1 = ((3/2)4х+1)2 = t2. Далее перепишем ур-ние с новой переменной t:

Снова получили квадратное ур-ние.

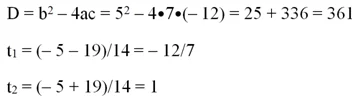
Возвращаемся к переменной х:

И снова первое ур-ние не имеет корней, так как при возведении положительного числа в степень не может получится отрицательное число. Остается решить второе ур-ние:

Ответ: – 0,25.

Методы решения показательных неравенств

Принцип решения других типов показательных неравенств состоит в том, что тем или иным образом их нужно свести к системам и/или совокупностям простейших. Чаще всего это делается путём преобразований с использованием свойств степени с действительным показателем, введением вспомогательной переменной, разложением выражений на множители или комбинацией всех этих методов. При подготовке к экзамену не забудьте повторить свойства степеней.

Пример 4

Решить неравенство:

Решение.

Вариант I.

Заметим, что 0,2 = \(\dfrac{1}{5}\) и уравняем основания левой и правой части.
\[\left(\frac{1}{5}\right)^{x^2 — 8x} здесь. )
\[-x^2 + 8x
Вариант II.

Можно было уравнять основания иначе, если заметить, что 5 = \(\dfrac{10}{2} = 1:\dfrac{2}{10} = \dfrac{1}{0,2}\). Тогда решение неравенства выглядело бы так:
\
Корни квадратного трёхчлена те же, ветви параболы направлены вверх, но так как теперь требуется, чтобы они находились выше оси абсцисс, то интервалы выполнения неравенства будут теми же: \((-\infty;1)\) и \((7; +\infty;)\).

Ответ:

Введение вспомогательной переменной

Пример 5

Решить неравенство:

Решение.

В последнем неравенстве неизвестная величина встречается дважды и только в показателе степени тройки, причем оба раза в одинаковой форме, поэтому можно продолжить решение методом введения вспомогательной переменной.

y

Ответ:

Замечание:

Вынесение множителя за скобки

Суть метода заключается в вынесении за скобки степени с наименьшим показателем.

Чтобы решить показательное уравнение, вынеся общий множитель, можно использовать тот факт, что если два числа имеют общий множитель, то на этот множитель можно сократить, разделив оба числа на один и тот же множитель. Это можно использовать для решения экспоненциальных уравнений путем исключения общих множителей, которые появляются как в основании, так и в показателе степени уравнения.

Например, рассмотрим следующее показательное уравнение:

Чтобы решить это уравнение, мы можем вынести общий множитель , разделив обе части уравнения на :

Это упрощает уравнение до:

Решением исходного уравнения является .

Это всего лишь один пример того, как решить показательное уравнение, вынеся общий множитель. Решим еще несколько примеров этим методом.

Пример 4

3^{3x+1}-2 \cdot 3^{3x}=27

Решение: наименьшим показателем степени является 3x, вынесем за скобки 3^{3x}3^{3x}(3-2)=273^{3x}=273^{3x}=3^33x=3x=1

Ответ: x=1

Пример 5

3^{2x-1}+3^{2x-2}-3^{2x-4}=315

Решение: наименьший показатель степени: 2x-4, тогда вынесем за скобки 3^{2x-4}:

3^{2x-4}(3^3+3^2-1)=3153^{2x-4}(27+9-1)=3153^{2x-4} \cdot 35=3153^{2x-4}=315:353^{2x-4}=93^{2x-4}=3^22x-4=22x=6x=3

Ответ: x=3

Показательные уравнения с разными основаниями

В практике порой встречаются показательные уравнения с разными основаниями, не сводимыми к друг к другу, и при этом с одинаковыми показателями степени. Выглядят они так: \(a^{f(x)}=b^{f(x)}\), где \(a\) и \(b\) – положительные числа.

Например:

\(7^{x}=11^{x}\)
\(5^{x+2}=3^{x+2}\)
\(15^{2x-1}=(\frac{1}{7})^{2x-1}\)

Такие уравнения легко можно решить делением на любую из частей уравнения (обычно делят на правую часть, то есть на \(b^{f(x)}\). Так делить можно, потому что положительное число в любой степени положительно (то есть, мы не делим на ноль). Получаем:

\(\frac{a^{f(x)}}{b^{f(x)}}\) \(=1\)

Дальше решаем с помощью свойств степени.

Пример. Решить показательное уравнение  \(5^{x+7}=3^{x+7}\)Решение:

\(5^{x+7}=3^{x+7}\)		Здесь у нас не получиться ни пятерку превратить в тройку, ни наоборот (по крайней мере, без использования логарифмов). А значит мы не можем прийти к виду \(a^{f(x)}=a^{g(x)}\). При этом показатели одинаковы. Давайте поделим уравнение на правую часть, то есть на \(3^{x+7}\) (мы можем это делать, так как знаем, что тройка ни в какой степени не будет нулем).
\(\frac{5^{x+7}}{3^{x+7}}\)\(=\)\(\frac{3^{x+7}}{3^{x+7}}\)		Теперь вспоминаем свойство \((\frac{a}{b})^c=\frac{a^c}{b^c}\) и используем его слева в обратном направлении. Справа же просто сокращаем дробь.
\((\frac{5}{3})^{x+7}\)\(=1\)		Казалось бы, лучше не стало. Но вспомните еще одно свойство степени: \(a^0=1\), иначе говоря: «любое число в нулевой степени равно \(1\)». Верно и обратное: «единица может быть представлена как любое число в нулевой степени». Используем это, делая основание справа таким же как слева.
\((\frac{5}{3})^{x+7}\)\(=\)  \((\frac{5}{3})^0\)		Вуаля! Избавляемся от оснований.
\(x+7=0\)		Пишем ответ.

Ответ: \(-7\).

Иногда «одинаковость» показателей степени не очевидна, но умелое использование свойств степени решает этот вопрос.

Пример. Решить показательное уравнение  \(7^{ 2x-4}=(\frac{1}{3})^{-x+2}\)Решение:

\(7^{ 2x-4}=(\frac{1}{3})^{-x+2}\)		Уравнение выглядит совсем печально… Мало того, что основания нельзя свести к одинаковому числу (семерка ни в какой степени не будет равна \(\frac{1}{3}\)), так еще и показатели разные… Однако давайте в показателе левой степени вынесем за скобку двойку.
\(7^{ 2(x-2)}=(\frac{1}{3})^{-x+2}\)		Помня свойство \((a^b )^c=a^{b·c}\) , преобразовываем слева: \(7^{2(x-2)}=7^{2·(x-2)}=(7^2 )^{x-2}=49^{x-2}\).
\(49^{x-2}=(\frac{1}{3})^{-x+2}\)		Теперь, вспоминая свойство отрицательной степени \(a^{-n}=\frac{1}{a}^n\), преобразовываем справа: \((\frac{1}{3})^{-x+2}=(3^{-1})^{-x+2}=3^{-1(-x+2)}=3^{x-2}\)
\(49^{x-2}=3^{x-2}\)		Аллилуйя! Показатели стали одинаковы! Действуя по уже знакомой нам схеме, решаем до ответа.

Ответ: \(2\).

Выделение устойчивого выражения

Давайте ещё раз посмотрим на это уравнение:

\

Что мы видим? Четвёрка возводится в разные степени. Но все эти степени — простые суммы переменной $x$ с другими числами. Поэтому необходимо вспомнить правила работы со степенями:

\

Проще говоря, сложение показателей можно преобразовать в произведение степеней, а вычитание легко преобразуется в деление. Попробуем применить эти формулы к степеням из нашего уравнения:

\

Перепишем исходное уравнение с учётом этого факта, а затем соберём все слагаемые слева:

\

В первых четырёх слагаемых присутствует элемент ${{4}^{x}}$ — вынесем его за скобку:

\

Осталось разделить обе части уравнения на дробь $-\frac{11}{4}$, т.е. по существу умножить на перевёрнутую дробь — $-\frac{4}{11}$. Получим:

\

Вот и всё! Мы свели исходное уравнение к простейшему и получили окончательный ответ.

При этом в процессе решения мы обнаружили (и даже вынесли за скобку) общий множитель ${{4}^{x}}$ — это и есть устойчивое выражение. Его можно обозначать за новую переменную, а можно просто аккуратно выразить и получить ответ. В любом случае, ключевой принцип решения следующий:

Хорошая новость состоит в том, что практически каждое показательное уравнение допускает выделение такого устойчивого выражения.

Но есть и плохая новость: подобные выражения могут оказаться весьма хитрыми, и выделить их бывает довольно сложно. Поэтому разберём ещё одну задачу:

\

Возможно, у кого-то сейчас возникнет вопрос: «Паша, ты что, обкурился? Здесь же разные основания — 5 и 0,2». Но давайте попробуем преобразовать степень с основание 0,2. Например, избавимся от десятичной дроби, приведя её к обычной:

\

Как видите, число 5 всё-таки появилось, пускай и в знаменателе. Заодно переписали показатель в виде отрицательного. А теперь вспоминаем одно из важнейших правил работы со степенями:

\

Тут я, конечно, немного слукавил. Потому что для полного понимания формулу избавления от отрицательных показателей надо было записать так:

\

С другой стороны, ничто не мешало нам работать с одной лишь дробью:

\

Но в этом случае нужно уметь возводить степень в другую степень (напомню: при этом показатели складываются). Зато не пришлось «переворачивать» дроби — возможно, для кого-то это будет проще.:)

В любом случае, исходное показательное уравнение будет переписано в виде:

\

Вот и получается, что исходное уравнение решается даже проще, чем ранее рассмотренное: тут даже не надо выделять устойчивое выражение — всё само сократилось. Осталось лишь вспомнить, что $1={{5}^{0}}$, откуда получим:

\

Вот и всё решение! Мы получили окончательный ответ: $x=-2$. При этом хотелось бы отметить один приём, который значительно упростил нам все выкладки:

Перейдём теперь к более сложным уравнениям, в которых присутствуют разные основания, которые вообще не сводятся друг к другу с помощью степеней.

Уравнения с заменой переменных

В ряде случаев для решения показательного уравнения следует ввести новую переменную. В учебных заданиях такая замена чаще всего (но не всегда) приводит к квадратному ур-нию.

Задание. Решите уравнение методом замены переменной

Заметим, что в уравнении стоят степени тройки и девятки, но 3 2 = 9. Тогда введем новую переменную t = 3 x . Если возвести ее в квадрат, то получим, что

C учетом этого изначальное ур-ние можно переписать:

Получили обычное квадратное ур-ние. Решим его:

Мы нашли два значения t. Далее необходимо вернуться к прежней переменной, то есть к х:

Первое ур-ние не имеет решений, ведь показательная функция может принимать лишь положительные значения. Поэтому остается рассмотреть только второе ур-ние:

Задание. Найдите корни ур-ния

Решение. Здесь в одном ур-нии стоит сразу три показательных функции. Попытаемся упростить ситуацию и избавиться от одной из них. Для этого поделим ур-ние на выражение 4 4х+1 :

Так как 1 4х+1 = 1, мы можем записать:

Обратим внимание, что делить ур-ние на выражение с переменной можно лишь в том случае, если мы уверены, что оно не обращается в ноль ни при каких значениях х. В данном случае мы действительно можем быть в этом уверены, ведь величина 4 4х+1 строго положительна при любом х

Вернемся к ур-нию. В нем стоят величины (9/4) 4х+1 и (3/2) 4х+1 . У них одинаковые показатели, но разные степени. Однако можно заметить, что

9/4 = (3/2) 2 , поэтому и (9/4) 4х+1 = ((3/2) 4х+1 ) 2 . Это значит, что перед нами уравнение с заменой переменных.

Произведем замену t = (3/2) 4х+1 , тогда (9/4) 4х+1 = ((3/2) 4х+1 ) 2 = t 2 . Далее перепишем ур-ние с новой переменной t:

Снова получили квадратное ур-ние.

Возвращаемся к переменной х:

И снова первое ур-ние не имеет корней, так как при возведении положительного числа в степень не может получится отрицательное число. Остается решить второе ур-ние:

Видео:Показательные уравнения. Видеоурок 11. Алгебра 10 классСкачать

Графическое решение показательных неравенств

Пример 6 — решить неравенство графически:

Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.

Функция — экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.

Функция — линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.

Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ()

Несложно заметить, что корнем данной системы является :

Таким образом, графики функций пересекаются в точке с аргументом, равным единице.

Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ: (рисунок 6.4)

Рис. 4. Иллюстрация к примеру 6

Итак, мы рассмотрели решение различных типовых показательных неравенств. Далее перейдем к рассмотрению более сложных показательных неравенств.

Список литературы

Мордкович А. Г. Алгебра и начала математического анализа. — М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. — М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. — М.: Просвещение.

Math. md . Mathematics-repetition. com . Diffur. kemsu. ru .

Домашнее задание

1. Алгебра и начала анализа, 10-11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 472, 473;

2. Решить неравенство:

3. Решить неравенство.

а x = b — простейшее показательное уравнение. В нем a
больше нуля и а
не равняется единице.

Графическое решение показательных уравнений

Не всякое показательное уравнение легко или вообще возможно решить аналитическим способом. В таких случаях выручает графическое решение уравнений.

Задание. Найдите графическим способом значение х, для которого справедливо равенство

Решение. Построим в одной системе координат графики у = 3х и у = 4 – х:

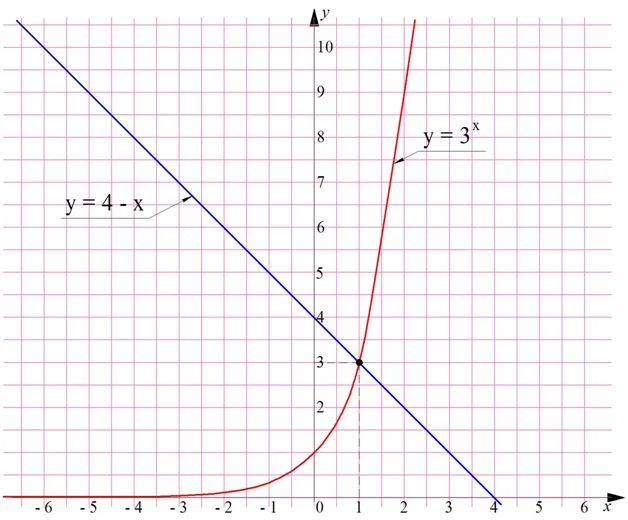
Видно, что графики пересекаются в одной точке с примерными координатами (1; 3). Так как графический метод не вполне точный, следует подставить х = 1 в ур-ние и убедиться, что это действительно корень ур-ния:

Получили верное равенство, значит, х = 1 – это действительно корень ур-ния.

Ответ: 1

Задание. Решите графически ур-ние

Решение. Перенесем вправо все слагаемые, кроме 2х:

Слева стоит показательная функция, а справа – квадратичная. Построим их графики и найдем точки пересечения:

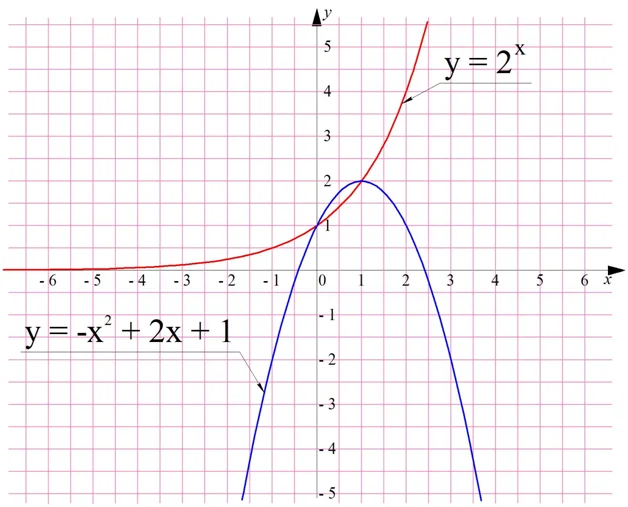
Видно, что у графиков есть две общие точки – это (0;1) и (1; 2). На всякий случай проверим себя, подставив х = 0 и х = 1 в исходное ур-ние:

Ноль подходит. Проверяем единицу:

И единица тоже подошла. В итоге имеем два корня, 0 и 1.

Ответ: 0; 1.

Решение типовых показательных неравенств

Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.

Одно из свойств показательной функции — она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:

Основание степени больше единицы, знак неравенства сохраняется.

Проиллюстрируем решение:

На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства.

Рис. 3. Иллюстрация к примеру 4

Преобразуем заданное неравенство согласно свойствам степени:

Приведем подобные члены:

Разделим обе части на :

Теперь продолжаем решать аналогично примеру 4, разделим обе части на :

Основание степени больше единицы, знак неравенства сохраняется:

Замена в показательных неравенствах

Мы разобрали все виды простейших степенных неравенств. Опираясь на эти знания, можно перейти к более сложным неравенствам, которые решаются при помощи замены переменной. В ЕГЭ по профильной математике такие примеры попадаются довольно часто.

Если вы раньше решали любые уравнения или неравенства на замену переменной, то разобраться будет совсем нетрудно. Давайте посмотрим на примерах:

Пример 12
$$ 4^x-29*2^x+168\le 0. $$
Согласно обычной логике в показательных неравенствах, приведем все показательные функции к одинаковому основанию. Здесь это сделать довольно легко:

$$ (2^2)^x-29*2^x+168 \le 0$$
$$ 2^{2x}-29*2^x+168 \le 0$$
Готово

Теперь обратите внимание, что \(2^{2x}=(2^x)^2\), согласно свойству степеней. Подставим:
$$ (2^x)^2-29*2^x+168 \le 0$$
В любом примере на замену переменной нужно найти одинаковые конструкции (выражения), зависящие от \(x\)

В нашем примере есть такая конструкция — \(2^x\).

Примеры решения

Задача 1

\(\sqrt{27}·3^{x-1}={(\frac{1}{3})}^{2x}\)

Решение

\(\sqrt{27}·3^{x-1}={(\frac{1}{3})}^{2x}\)

\(27 = 3^3\)

\(\sqrt{3^3}·3^{x-1}={(\frac{1}{3})}^{2x}\)

\(\sqrt{a}=a^{\frac{1}{n}}\)

\(\sqrt{3^3}=({3^3})^{\frac{1}{2}}\)

\(((a^b )^c=a^{bc}\)

\({(3^3)}^{\frac{1}{2}}=3^{3 \cdot \frac{1}{2}}=3^{\frac{3}{2}}\)

\(3^{\frac{3}{2}}\cdot 3^{x-1}=(\frac{1}{3})^{2x}\)

\(a^b·a^c=a^{b+c}\)

\(3^{\frac{3}{2}}·3^{x-1}=3^{\frac{3}{2}+ x-1}=3^{1,5 + x-1}=3^{x+0,5}\)

\(3^{x+0,5}=(\frac{1}{3})^{2x}\)

\(a^{-n}=\frac{1}{a^n}\)

\(\frac{1}{a^n} =a^{-n}\)

\(\frac{1}{3}=\frac{1}{3^1} =3^{-1}\)

\(3^{x+0,5}=(3^{-1} )^{2x}\)

\((a^b )^c=a^{bc}\)

\((3^{-1} )^{2x}=3^{(-1)·2x}=3^{-2x}\)

\(3^{x+0,5}=3^{-2x}\)

x+0,5=-2x

Ответ: \(x=-\frac{1}{6}\)

Задача 2

Применяя стандартный алгоритм действий и свойства степенных функций, необходимо вычислить значение х в следующем математическом соотношении: \(2^{x+3}+2^{x+2}-2^{x+1}=160\)  

Решение

\(2^{x+3}+2^{x+2}-2^{x+1}=160\)

\(a^b \cdot a^c=a^{b+c}\)

\(2^x \cdot 2^3+2^x \cdot 2^2-2^x \cdot 2^1=160\)

\(2^x (2^3+2^2-2^1 )=160\)

\(2^x (8+4-2)=160\)

\(10 \cdot 2^x=160\)

\(2^x=16\)

\(2^x=2^4\)

Ответ: 4.

Задача 3

С помощью ранее рассмотренной последовательности действий необходимо выполнить математические преобразования с применением изученных свойств показательных функций при решении следующего степенного равенства: \(4^{x+0,5}-5·2^x+2=0\) 

Решение

\(4^{x+0,5}-5·2^x+2=0\)

\(а^b \cdot a^c=a^{b+c}\)

\(4^x·4^{0,5}-5·2^x+2=0\)

\(4=2^2\)

\((2^2 )^x·(2^2 )^{0,5}-5·2^x+2=0\)

\((2^2 )^x=2^{2x}=2^{x·2}=(2^x )^2\)

\((2^2 )^{0,5}=2^{2·0,5}=2^1=2\)

\(2·(2^x )^2-5·2^x+2=0\)

\(t=2^x\)

\(2t^2-5t+2=0\)

\(t_1=2\)

\(t_2=\frac{1}{2}\)

\(2^x=2\)

\(2^x=\frac{1}{2}\)

\(2^x=2^1\)

\(2^x=2^{-1}\)

\(x_1=1\)

\(x_2=-1\)

Простейшие показательные неравенства, методика решения, пример

На основании вышесказанного приведем методику решения простейших показательных неравенств:

Методика решения неравенств:

Уравнять основания степеней;

Сравнить показатели, сохранив или изменив на противоположный знак неравенства.

Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.

Основание степени больше единицы, значит, знак неравенства сохраняется:

Преобразуем правую часть согласно свойствам степени:

Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:

Для решения квадратного неравенства решим соответствующее квадратное уравнение:

По теореме Виета находим корни:

Ветви параболы направлены вверх.

Таким образом, имеем решение неравенства:

Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:

Основание степени больше единицы, знак неравенства не меняется, получаем:

Напомним методику решения таких неравенств.

Рассматриваем дробно-рациональную функцию:

Находим область определения:

Находим корни функции:

Функция имеет единственный корень,

Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:

Рис. 2. Интервалы знакопостоянства

Таким образом, получили ответ.

Ответ:

Простейшие примеры

Чтобы научиться решать задачи сложного уровня, нужно довести решение элементарных неравенств до автоматизма. Поэтому необходимо самостоятельно потренироваться в вычислении однотипных простых заданий.

Например, нужно решить неравенство вида: 8P>0,25. Для нахождения множества решений уравнение переписывают следующим образом: (23)p > 25/1000. Правую часть можно сократить на 25 в итоге она упростится до простой дроби 1/40. После дальнейшего преобразование неравенство примет вид: (23)p > 25,3.

Так как функция вида 2f (x) является возрастающей, то график при переходе от одной части неравенства к другому знак не изменяет. Используя правило, выражение можно переписать как 3*p > 5,3. Отсюда p > 5,3/3. Ответом на поставленную задачу будет диапазон от 1,76 до плюс бесконечности.

По аналогичному алгоритму решаются и другие задачи подобного типа. Например, нужно решить неравенство: 0,53x+4 ≥ 4. Вначале необходимо попробовать привести обе части к одинаковому основанию. Существует приём, согласно которому, если в уравнении есть степень с основанием в виде десятичной дроби, то её нужно привести к виду обыкновенной.

Основание 0,5 можно представить как 1/2, а четвёрку как два в квадрате или (1/2)-2. Тогда неравенство примет вид: (1/2)3x+4 ≥ (1/2)-2. Так как основание 1/2 больше нуля, но меньше единицы, то знак в уравнении меняется на противоположный. В итоге получается неравенство: 3x+4 ≤ -2. После группировки однородных членов в правой и левой части получится выражение: x ≤ -2. Это и есть ответ на поставленную задачу. Записать его можно и как x є (- ∞;-2 ).

Поняв метод, можно переходить к неравенствам более сложного вида. Например, 58m+1+58m+1 < 130. Используя теорию свойств степени, заданное уравнение можно переписать в виде равносильного неравенства: 58m *5 +58m*5-1 < 130. В левой части есть общий множитель, который можно вынести за скобку: 58x * (5+(1/5)) < 130. Выполнив действие в скобках, выражение можно упростить до вида: 58x * 5(1/5) < 130.

О методе рационализации.

Метод рационализации для показательных неравенств сводится к следующему:

Очевидно, что в случае числового основания степени это решение не является более простым и более понятным, чем решение предыдущих примеров. Метод рационализации существенно сокращает объём рассуждений и выкладок, когда в основании степени также как и в её показателе находятся неизвестные переменные величины. И хотя такие неравенства относятся к более сложным типам, чем те, которые бывают на ЕГЭ даже профильного уровня, рассмотрим пример.

Пример 7

Решить неравенство:
\

Решение.

Обратите внимание – для решения показательных неравенств методом рационализации тоже нужно выравнивать основания степеней или, как в этом примере, иметь их одинаковыми по условию задачи. методом интервалов

методом интервалов.

Первое неравенство

Окончательно имеем

Обратите внимание – дробь с неизвестными в знаменателе можно сокращать только после того, как записали ОДЗ. Мы ОДЗ не записывали, поэтому сокращать не будем

Тот факт, что на 0 делить нельзя, отметим непосредственно на числовой оси.

Ответ:

Чтобы продолжить решение показательных неравенств, перейдите по ссылкамПримеры неравенств из банка заданий ЕГЭ

Понятие и обозначения

Неравенство является выражением обратным по смыслу равенству. Если второе обозначает, что два сравниваемых объекта численно равны друг другу, то первое подчёркивает их различие. Обозначается оно с помощью математических знаков: больше, меньше или их комбинацией с равно. Выражения с переменными могут быть верными, то есть при подстановке неизвестных заданное знаком условие выполняется, или неверными. Решить уравнение — найти все возможные корни, делающие его тождественным, или доказать, что их нет.

Любое неравенство с несколькими неизвестными можно представить в виде функции, в которой переменные определяются зависимостью. В математике функциональность в общем виде записывается выражением: Y = f (X). В нём X определяет область значений, а Y их множество. Уравнение, в состав которого входят степени называют показательным: f (X) = nx, где n — основание степени, которое не должно быть равное единице и быть меньше нуля; x — показатель разряда.

Таким образом, формулы простейших показательных неравенств имеют вид: nx < m или nx > m, где n > 0 и n ≠ 1, x — искомая переменная. Для выражения характерно следующее:

• область чисел, превращающая выражение в верное, определяется диапазоном функции;
• правильные решения входят в промежуток, лежащий в диапазоне от нуля до плюс бесконечности, то есть являются положительными числами;
• понятие наибольшего и наименьшего значения для выражения не существует;
• показательное уравнение не может быть нечётным или чётным;
• график, изображённый в декартовой системе координат, пересекает ось ординат в точке (0; 1);
• описывающая функция не имеет нулей и не может быть нечётной или чётной.

График, соответствующий выражению, может быть убывающим или возрастающим. Для любого числового показателя X-предел определяется как последовательность значений, стремящихся к абсциссе. При рассмотрении экспоненты используют определение через предел, поэтому сложные неравенства решают с использованием логарифмов.