Содержание
-
Слайд 1
Линейное уравнение
с двумя переменными.
График линейного уравнения
с двумя переменными -
Слайд 2
проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала;
развивать познавательные способности учеников; расширение кругозора учащихся; развитие внимания, логического мышления.
воспитывать активность, самостоятельность; воспитание основ здорового образа жизни, формирование бережного отношения учащихся к своему здоровью; -
Слайд 3
-
Слайд 4
Повторение:
1) Дать определение линейного уравнения
с двумя переменными.
2) Что называется решением уравнения с двумя переменными?
3) Какое уравнение называется равносильным данному?
4) Что называется графиком уравнения с двумя переменными?Дальше
-
Слайд 5
Линейным уравнением с двумя переменными называется уравнение вида ах+by=c,
где хи у – переменные,
а, bи с некоторые числа. -
Слайд 6
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
-
Слайд 7
Уравнения с двумя переменными, имеющие одни и те же корни, называются равносильными.
-
Слайд 8
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
-
Слайд 9
Историческая справка.
Рене Декарт (1596-1650)− французский философ, математик и физик. Создал основы аналитической геометрии, ввел понятие переменной величины, разработал метод координат. Осуществил связь алгебры с геометрией.
Пьер Ферма (1601-1665) − французский математик, один из создателей аналитической геометрии и теории чисел. Занимался теорией решения алгебраических уравнений с несколькими переменными.
-
Слайд 10
Ответ: а)3х – у = 14
г) 5х + 2у = 16 -
Слайд 11
2х + 5у = 12
а)А(-1; -2), б)В(2; 1), в)С(4; -4), г)D(11; -2).
Ответ: г)D(11; -2).
-
Слайд 12
x
8
6
4
2
-2
е ж з и к л м
а б в г д
у ф х ц ч ш щ
й э ю я п р с
н о т й(6;4) (-2;-2) (4;4) (-2;-2) (4;6) (-6;4) (0;2)
М О Л О Д Е Цy
№2. «Угадай слово»-8 -6 -4 -2 0 2 4 6 8
-
Слайд 13
№ 1045 (д),
№ 1048 (г, д),
№ 1050 (г). -
Слайд 14
№1045. д) Принадлежит ли графику уравнения 3х+4у=12 точка D(0,3)?
3х+4у=12
3*0+4*3=12,
12=12 (да). -
Слайд 15
г) 0,5у-х=1,
0,5у=1+х,
у=2+2хд) 1,2х=-4,8,
х=-4х
у
02
1
3
4
1
2
-1
-2
-3
-40,5у-х=1
1,2х=-4,8
-
Слайд 16
№1050. Постороить график уравнения
г) (х+у)-(х-у)=4,
х+у-х+у=4,
2у=4,
у=2. (х+у)-(х-у)=4х
у0
21
-
Слайд 17
№4. Самостоятельная работа
Вариант 1
Трудность 1
1.Выразите переменную у через х: у+4х=6.
2. Принадлежит ли графику
уравнения 4х+2у=6 точка А(-2;3)?
Трудность 2
3. Выразите переменную
х через у: 10у-6х=30.
4. Построить график уравнения 2х+у=4.
Трудность 3
Сахар расфасован в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получить 20 кгсахара?Вариант 2
Трудность 1
1.Выразите переменную у через х: у-3х=6 .
2. Принадлежит ли графику
уравнения 4х+2у=6 точка В(-1;5)?
Трудность 2
3. Выразите переменную
х через у: 12у-4х=20.
4. Построить график уравнения
5х + у – 4 = 0 .
Трудность 3
Ваня купил ручки по 5 руб.
И тетради по 7 руб. Сколько
ручек и тетрадей купил Ваня,
если за всю покупку он заплатил 44 руб.? -
Слайд 18
На прямой, являющейся графиком уравнения 3х+1=у, взята точка, абсцисса которой равна 0. Найдите ординату этой точки.
-
Слайд 19
Вариант 1
1. у=6-4х
2. нет
3. х=-5+5/3у
4.
Вариант 2
1. у=6+3х
2. да
3. х=-5+3у
4.у
х
0
2
4х
у
0
1
-1
42 (3кг) и 7 (2кг);
4 (3кг) и 4 (2кг);
6 (3кг) и 1 (2кг);
5. 6 ручек и 2 тетради -
Слайд 20
у=3х+1
х
у
01
-1
-2
Ответ: (0;1) -
Слайд 21
-
Слайд 22
п.41,42
(1) № 1049 (а, б), 1052;
(2) №1054(6), 1055 (а);
(3 ) № 1141.
Домашняя работа: -
Слайд 23
Спасибо за урок!
Посмотреть все слайды
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки или «железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
| x + 5y = 7 |
| 3x − 2y = 4 |
Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».
Чтобы выразить неизвестное, нужно выполнить два условия:
- перенести неизвестное, которое хотим выразить, в левую часть уравнения;
- разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.
Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.
При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
| x = 7 − 5y |
| 3x − 2y = 4 |
Теперь, вместо « x » подставим во второе уравнение полученное выражение « x = 7 − 5y » из первого уравнения.
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение « 3(7 − 5y) − 2y = 4 » отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*) .
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 (*) |
Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.
| x + 5y = 7 |
| 3x − 2y = 4 |
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 |
| + => | x + 5y + 3x − 2y = 11 |
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
| x + 5y = 7 |
| 3x − 2y = 4 |
Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».
Для этого умножим первое уравнение на « −3 ».
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) |
| 3x − 2y = 4 |
| x · (−3) + 5y · (−3) = 7 · (−3) |
| 3x − 2y = 4 |
| −3x −15y = −21 |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 |
| + => | − 3x − 15y + 3x − 2y = −21 + 4 |
| 3x − 2y = 4 | −17y = −17 |:(−17) |
| y = 1 |
Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Пример решения системы уравнения способом подстановки
Выразим из первого уравнения « x ».
| x = 17 + 3y |
| x − 2y = −13 |
Подставим вместо « x » во второе уравнение полученное выражение.
| x = 17 + 3y |
| (17 + 3y) − 2y = −13 (*) |
Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».
| x = 17 + 3y |
| y = −30 |
| x = 17 + 3 · (−30) |
| y = −30 |
| x = 17 −90 |
| y = −30 |
| x = −73 |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 |
| 2x −2y + 3y = 4 |
| 2x − 3y = −4 |
| 2x + y = 4 |
Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».
Для этого достаточно умножить первое уравнение на « −1 ».
| 2x − 3y = −4 | ·(−1) |
| 2x + y = 4 |
| 2x · (−1) − 3y · (−1) = −4 · (−1) |
| 2x + y = 4 |
| −2x + 3y = 4 |
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только « y » в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 |
| + => | − 2x + 3y + 2x + y = 4 + 4 |
| 2x + y = 4 | 4y = 8 | :4 |
| y = 2 |
Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».
Источник
Понятие системы и ее розвязків
Определение: Если ставится задача найти все общие развязки двух (или более) уравнений с одной или несколькими переменными, то говорят, что надо розвязати систему уравнений.
Определение: Розвязком системы — такое значение переменной или такой упорядоченный набор значений зміниих, что удовлетворяет сразу всем уравнениям системы, то есть розвязком системы двух или более уравнений с неизвестными называется такое упорядоченное множество множество чисел, при подстановке которых в систему вместо неизвестных все уравнения превращаются в верные числовые равенства.
Определение: Розвязати систему уравнений — найти все ее развязки или доказать, что их нет.
Если система не имеет решения, то она несовместима.
Примеры систем
— система двух уравнений с двумя переменными
Пара то есть —решение системы
— система трех уравнений с тремя переменными
Тройка то есть — один из розвязків системы
Способ сложения
Идея решения остается неизменной — избавиться в одном из уравнений от одного из неизвестных. Путь достижения этой цели в способе сложения заключается в подборе коэффициентов, на которые надо умножить обе части уравнений, чтобы коэффициенты при одном из неизвестных были одинаковы по модулю, но различны по знаку. После этого уравнения складываются и решается новая система уравнений, которая будет тождественна исходной, поскольку все проводимые операции тождественны.
5x+6y = 60 x-y = 1
Как и в первом случае, избавимся во втором уравнении от неизвестной y, для этого умножим обе части второго уравненя на 6:
5x+6y = 60 6x-6y = 6
Теперь складываем первое и второе уравнения, и получаем новую систему уравнений:
5x+6y = 60 11x = 66
В новой системе уравнений первое уравнения взято из исходной системы, а второе является суммой уравнений после выполненных преобразований. Дальнейший ход решения полностью аналогичен способу подстановки:
5x+6y = 60 x = 6 5(6)+6y = 60 x=6 30+6y = 60 x=6 6y = 60-30 x=6 y=5 x=6
Как решать систему уравнений графическим способом
Метод предусматривает графическое определение общих точек пересечения графиков. Система может иметь одно решение в случае пересечения прямых, несколько решений — при графике из параллельных прямых и множество решений — при совпадении графиков.
Пример 1
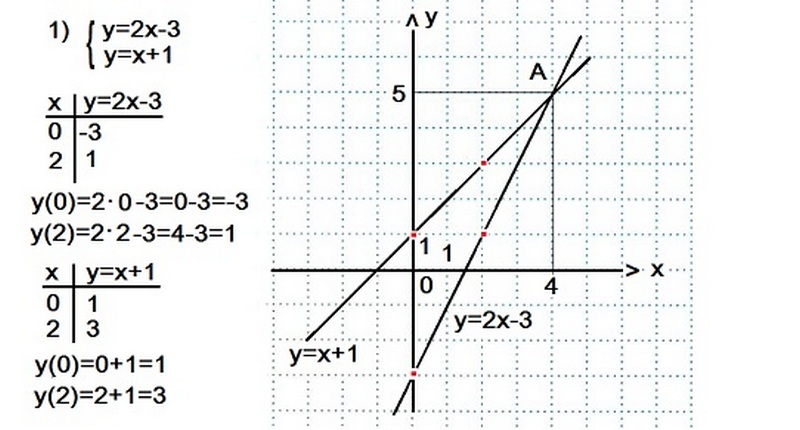
Для начала определимся с координатами х;у и нарисуем прямые. Функции имеют общую точку А (4;5), что будет решением системы.
Ответ: х=4; у=5
Пример 2
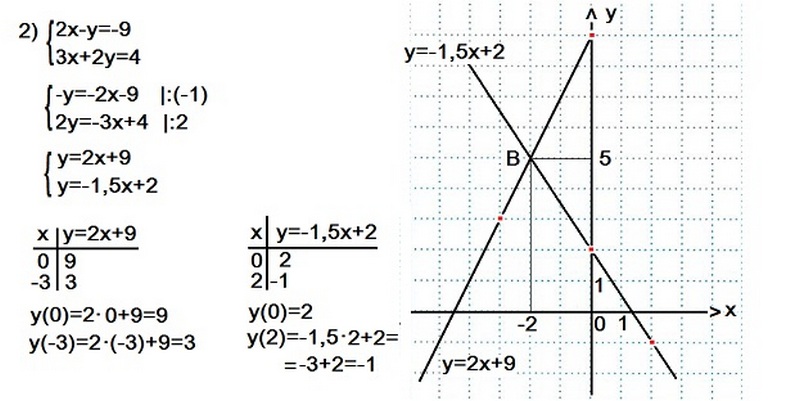
Чтобы решить второй пример необходимо выразить у через х, а затем определить точки прохождения прямых. Графики уравнений пересекутся в точке В (-2; 5).
Ответ: х=-2; у=5
Пример 3, где решений у системы нет.
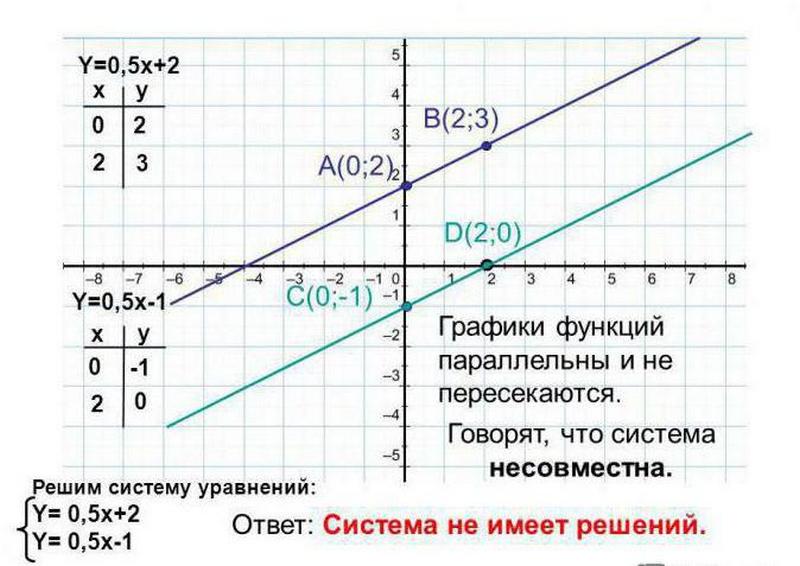
Последний графический способ считается неточным и системы с квадратами и корнями им не решить.
Математика — это просто!
- УРАВНЕНИЯ и ТОЖДЕСТВА
-
· Алгебраические равенства
· Работа со скобками
· Уравнение с одним неизвестным
· Тождества
· Линейное уравнение
· Система из 2 уравнений
· Квадратное уравнение
· Теорема Виета
· Биквадратное уравнение
· Примеры решения задач
· Уравнение вида sin(x)=y
· Уравнение вида cos(x)=y
· Уравнение вида tg(x)=y; ctg(x)=y
· Показательные уравнения
· Логарифмические уравненияНЕРАВЕНСТВА
· Числовые неравенства
· Сложение и умножение
· Решение неравенств
· Числовые промежутки
· Модуль числа
· Квадратные неравенства
· Тригонометрические неравенства
· Показательные неравенства
· Логарифмические неравенства - НАТУРАЛЬНЫЕ ЧИСЛА
- ДРОБИ
- ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ
- ФУНКЦИИ
- ТРИГОНОМЕТРИЯ
- ПЛОСКИЕ ФИГУРЫ
- ВЫСШАЯ МАТЕМАТИКА
Графический способ решения
Каждое из уравнений, входящих в систему, можно рассматривать как некую формулу, которая задает определенную функцию (понятие функции будет рассмотрено чуть позже).
Поскольку функция имеет свой график, задаваемый ее формулой, его можно построить на координатной плоскости.
Так как уравнения у нас линейные, то и график у линейной функции будет в виде прямой.
В результате мы получим две прямые, координаты точки пересечения которых и будут являться решением нашей системы уравнений.
Надо сказать, что к данному методу прибегают достаточно редко, поскольку он достаточно неудобен и зачастую дает приблизительные результаты.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
x — 4y = 2;
x = 2 + 4y.
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3(2 + 4y) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Ответ: x = 6, y = 1.
Основные виды систем уравнений
В математике насчитывается достаточно много видов систем уравнений. Для более удобного их изучения и нахождения решений их разделяют на несколько групп с определёнными характеристиками.
Классификация помогает рассматривать системы уравнений разных видов. Первый вариант – это классифицирование по количеству уравнений в системе. Если оно всего одно, то его называют обычным уравнением. Если уравнений несколько, тогда речь идет о системе.
Отличительным критерием для другого вида классификации является количество переменных. Если переменная одна, значит это уравнение с одной неизвестной, если их две – то с двумя неизвестными и т.д.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
| x — 4y = 2 | |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
| 2 — x | = | 16 — 3x |
| -4 | -2 |
Решаем уравнение, чтобы узнать значение x:
|
||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Ответ: x = 6, y = 1.
Метод сложения
Очевидно, что не всегда в ур-нии можно выразить одну переменную через другую. Такую ситуацию можно, например, наблюдать в сис-ме
Однако здесь в каждом ур-нии есть слагаемое 6у2, взятое с разными знаками. За счет этого сис-му можно решить методом сложения, ведь при сложении левых частей ур-ний слагаемые 6у2 и (– 6у2) сократятся, что позволит исключить переменную у из ур-ния. Для этого надо сложить по отдельности левые и правые части ур-ний и получить новое ур-ние:
(3х2 – 6у2 + 3х) + (– 2х2 + 6у2) = –18 + 22
3х2 – 6у2 + 3х – 2х2 + 6у2 = 4
х2 + 3х = 4
х2 + 3х – 4 = 0
Получили ур-ние, не содержащее у. Его можно решить как обычное квадратное ур-ние:
D = b2– 4ас = 32 – 4•1•(– 4) = 9 + 16 = 25
х1 = (– 3 – 5)/2 = – 4
х2 = (– 3 + 5)/2 = 1
Нашли два значения х. Подставляя его второе ур-ние, получим
при х = – 4:
– 2•(– 4)2 + 6у2 = 22
6у2 = 22 + 32
у2 = 9
у1 = 3 или у2 = – 3
при х = 1:
– 2•12 + 6у2 = 22
6у2 = 22 + 2
у2 = 4
у3 = – 2 или у4 = 2
Имеем 4 решения сис-мы (– 4; 3), (– 4; – 3), (1; – 2), (1; 2).
Мы рассмотрели простейший случай использования метода сложения уравнений, когда ур-ния сис-мы можно сложить сразу. Однако порою их надо сначала умножить на какие-то числа, и лишь потом складывать.
Пример. Укажите решение для сис-мы:
Решение. Сразу складывать эти ур-ния нет смысла, потому что при этом не исчезнет ни одна переменная. Напомним, что обе части любого ур-ния можно умножить на число, не равное нулю, и в результате получится равносильное ур-ние. Поэтому второе ур-ние умножим на (– 2):– 4х2+ 2у2 = – 2
А вот теперь есть смысл сложить его с первым ур-нием, так как у них есть слагаемые 2у2 с противоположными знаками:
(3х2 – 2у2) + (– 4х2 + 2у2) = 1 – 2
–х2 = – 1
х2 = 1
х = – 1 или х = 1
Полученные значения х будем подставлять в другое ур-ние, например, в 2х2 – у2 = 1 (на самом деле можно выбрать любое другое из ур-ний сис-мы).
При х = – 1:
2(– 1)2 – у2 = 1
у2 = 1
у1 = – 1 или у2 = 1
Теперь подставим х = 1:
2•12 – у2 = 1
у2 = 1
у3 = – 1 или у4 = 1
В итоге получаем 4 решения: (– 1; – 1), (– 1; 1), (1; – 1) и (1; 1)
Ответ:(– 1; – 1), (– 1; 1), (1; – 1), (1; 1).
Порою метод сложения и метод подстановки следует использовать одновременно.
Пример. Решите систему методом сложения:
Решение: постараемся избавиться от слагаемых с буквенной частью ху. Для этого умножим второе ур-ние на (– 2):
– 2х – 2у – 2ху = 12
Сложим его с первым ур-нием:
(3х + у + 2ху) + (– 2х – 2у – 2ху) = – 6 + 12
х – у = 6
исключить переменную не удалось, однако мы получили линейное ур-ние. Выразим из него у:
у = х – 6
х + у + ху = – 6
х + (х – 6) + х(х – 6) = – 6
х2 – 4х – 6 = – 6
х2 – 4х = 0
х(х – 4) = 0
х = 0 или х – 4 = 0
х1 = 0 или х2 = 4
Подставим полученные результаты в выражение у = х – 6
у1 = х1 – 6 = 0 – 6 = – 6
у2 = х2 – 6 = 4 – 6 = – 2
Получили два решения: (0; – 6) и (4; – 2).
Ответ: (0; – 6) и (4; – 2).
Фактчек
Системой уравнений являются несколько уравнений с одной и более переменными, выполняющиеся одновременно.
Для решения систем уравнений используют три метода: графический, метод сложения и метод подстановки. Графический метод очень неточный, поэтому он удобен только для нахождения количества решений.
Метод сложения заключается в сложении двух уравнений так, чтобы получить одно из уравнений в системе с одной переменной и второе уравнение перенести из прошлой системы.
Для метода подстановки нужно выразить из любого уравнения одну неизвестную, подставить ее значение вместо этой переменной в другое уравнение и аналогично составить систему из нового уравнения и одного из уравнений начальной системы
Матричная запись[]
СЛАУ может быть представлена и в матричной форме:
-
(a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn)(x1x2⋮xn)=(b1b2⋮bm){\displaystyle
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix}
}
или:
- Ax=b{\displaystyle Ax=b}.
Здесь A{\displaystyle A} — это матрица системы, x{\displaystyle x} — столбец неизвестных, а b{\displaystyle b} — столбец свободных членов. Если к матрице A{\displaystyle A} приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
Последовательность действий:
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
Этапы решения:
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Что такое система уравнений?
К определению системы уравнений будем подбираться постепенно. Сначала лишь скажем, что его удобно дать, указав два момента: во-первых, вид записи, и, во-вторых, вложенный в эту запись смысл. Остановимся на них по очереди, а затем обобщим рассуждения в определение систем уравнений.
Пусть перед нами несколько каких-нибудь уравнений. Для примера возьмем два уравнения 2·x+y=−3 и x=5. Запишем их одно под другим и объединим слева фигурной скобкой:
Записи подобного вида, представляющие собой несколько расположенных в столбик уравнений и объединенных слева фигурной скобкой, являются записями систем уравнений.
Что же означают такие записи? Они задают множество всех таких решений уравнений системы, которые являются решением каждого уравнения.
Не помешает описать это другими словами. Допустим, какие-то решения первого уравнения являются решениями и всех остальных уравнений системы. Так вот запись системы как раз их и обозначает.
Теперь мы готовы достойно воспринять определение системы уравнений.
Определение.
Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения системы.
Аналогичное определение приведено в учебнике , однако там оно дано не для общего случая, а для двух рациональных уравнений с двумя переменными.
Проверь себя
Задание 1. Решить систему уравнений {x2+y=5 6x-y=2
- (-7; -44), (1; 4)
- (8; 15), (4; 1)
- (11; -4), (1; 2)
- (-7; -4), (3; 4)
Задание 2.Решить систему уравнений {xy+x=0 x-y=7
- (7; -2), (6; -1)
- (0; -2), (5; -11)
- (-7; 0), (6; 0)
- (0; -7), (6; -1)
Задание 3.Решить систему уравнений {x+xy2=0 x-y=5
- (2; 3)
- (0; -8)
- (0; -5)
- (2; -5)
Задание 4.Решить систему уравнений {x+3y=16 xy=5
- (15;1)
- (10;2)
- (8;2)
- (15;2)
Задание 5.Решить систему уравнений {x-yx+y=0 x+y2=2
- (-2; -3), (1; 1), (1; 0), (-2; 2)
- (-2; -2), (-1; 1), (1; -1), (2; 2)
- (-1; -2), (1; 2), (1; 0), (-1; 2)
- (-2; -2), (1; 1), (1; -1), (-2; 2)
Ответы: 1. — 1; 2. — 4; 3. — 3; 4. — 2; 5. — 4.
Что называется решением системы уравнений?
К системам уравнений непосредственно относится термин «решение системы уравнений». В школе дается определение решения системы уравнений с двумя переменными :
Определение.
Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы.
Например, пара значений переменных x=5, y=2 (ее можно записать как (5, 2)) является решением системы уравнений по определению, так как уравнения системы при подстановке в них x=5, y=2 обращаются в верные числовые равенства 5+2=7 и 5−2=3 соответственно. А вот пара значений x=3, y=0 не является решением этой системы, так как при подстановке этих значений в уравнения, первое из них обратится в неверное равенство 3+0=7.
Аналогичные определения можно сформулировать и для систем с одной переменной, а также для систем с тремя, четырьмя и т.д. переменными.
Определение.
Решением системы уравнений с одной переменной будет значение переменной, являющееся корнем всех уравнений системы, то есть, обращающее все уравнения в верные числовые равенства.
Приведем пример. Рассмотрим систему уравнений с одной переменной t вида . Число −2 является ее решением, так как и (−2)2=4, и 5·(−2+2)=0 – верные числовые равенства. А t=1 – не является решением системы, так как подстановка этого значения даст два неверных равенства 12=4 и 5·(1+2)=0.
Определение.
Решением системы с тремя, четырьмя и т.д. переменными называется тройка, четверка и т.д. значений переменных соответственно, обращающая в верные равенства все уравнения системы.
Так по определению тройка значений переменных x=1, y=2, z=0 – решение системы , так как 2·1=2, 5·2=10 и 1+2+0=3 — верные числовые равенства. А (1, 0, 5) не является решением этой системы, так как при подстановке этих значений переменных в уравнения системы второе из них обращается в неверное равенство 5·0=10, да и третье тоже 1+0+5=3.
Заметим, что системы уравнений могут не иметь решений, могут иметь конечное число решений, например, одно, два, …, а могут иметь бесконечно много решений. В этом Вы убедитесь по мере углубления в тему.
Учитывая определения системы уравнений и их решений можно заключить, что решение системы уравнений представляет собой пересечение множеств решений всех ее уравнений.
В заключение приведем несколько связанных определений:
Определение.
Система уравнений называется несовместной, если она не имеет решений, в противном случае система называется совместной.
Определение.
Система уравнений называется неопределенной, если она имеет бесконечно много решений, и определенной, если имеет конечное число решений, либо не имеет их вообще.
Эти термины вводятся, например, в учебнике , однако в школе применяются довольно редко, чаще их можно услышать в высших учебных заведениях.
Дальше не помешает познакомиться с равносильными системами уравнений, а уже потом можно будет переходить к процессу нахождения решений систем уравнений.
Список литературы.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 17-е изд., доп. — М.: Мнемозина, 2013. — 175 с.: ил. ISBN 978-5-346-02432-3.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- А. Г. Курош. Курс высшей алгебры.
- Ильин В. А., Позняк Э. Г. Аналитическая геометрия: Учеб.: Для вузов. – 5-е изд. – М.: Наука. Физматлит, 1999. – 224 с. – (Курс высшей математики и мат. физики). – ISBN 5-02-015234 – X (Вып. 3)
Некогда разбираться?
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Видео:АЛГЕБРА 9 класс: Уравнение с двумя переменными | ВидеоурокСкачать

Схема решению систем уравнений
Графический метод
- Выполняем равносильные преобразования, так, чтобы было удобно построить график функции. Например:
- Строим графики.
- Находим точки пересечения графиков. Координаты этих точек и есть розвязком данной системы уравнений.
Метод подстановки
- Из одного уравнения системы выражаем одну переменную через другую, всегда выбираем удобную переменную. Например, из уравнения выражаем переменную а не наоборот.
- Найденное значение подставляем в другое уравнение системы и получаем уравнение с одной переменной.
- Розвязуємо полученное уравнение
- Найденное значение подставляем в выраженное уравнение, и находим значение второй переменной.
Метод сложения
- Урівнюємо коэффициенты при одной из переменных путем по членного умножения обоих уравнений на множители, подобранные соответствующим образом.
- Добавляем (или отнимаем) почленно два уравнения системы, тем самым исключается одна переменная.
- Розвязуємо полученное уравнение.
- Подставляем найденное значение переменной в любое из исходных уравнений.





























