Свойства функций в задачах с параметрами

Принцип определения наибольших и наименьших значений функции на отрезках

Рассмотрим последовательность проведения основных операций, для определения нужных нам числовых значений для определенной функции:

Для начала задается область определения функции. Далее необходимо провести ее анализ и проверить входит ли в ее пределы заданный отрезок.
Определяем точки, на отрезках, в которых не существует первой точки. Это показательно, для функций у которых аргумент обозначается в виде модуля. А также, данную характеристику можно встретить у степенных функций, у которых показатель — простое рациональное числовое значение.
Вычисляем определение производной функции и приравниваем ее к нулевому значению. Составляем нужное нам уравнение и подбираем корневые значения. Если ни одна стационарная точка не попадает в заданный нами отрезок, нужно применить другие действия. Расписанные в пунктах 4 и 5.
Вычисляем значения в стационарных точках, если они не существуют в первой производной
В конечном итоге мы получаем ряд числовых значений. Далее начинаем выбирать самое максимальное и минимальное значение, для функции, которые мы хотим определить.

Весь приведенный алгоритм решения, рассмотрим на конкретном примере, для лучшего восприятия информации.

Задано условие задачи:

Функция следующего вида \

Необходимо определить значения, которые будут отражать максимальное и минимальное числовое значение на заданном отрезке. Отрезок отображает следующие значения ]-4;1].

Выполняем все необходимые действия, применяя наш уже изученный алгоритм решения.

Определяем область функции, которая равняется действительным числам, отличным от нулевого значения.

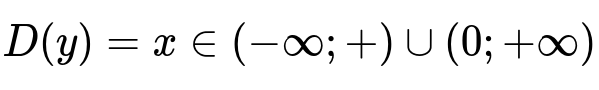
Два отрезка, определенно, будут находится в области определения. Затем по известным формулам, определяем производное значение функции.

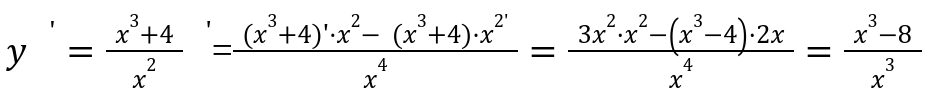
Из уравнения мы определили, что производная значения функции, будет существовать во всех точках заданных отрезках.

Далее, при помощи определенного нами уравнения, вычислим значения стационарных точек.

Уравнение имеет только один корень действительного числа, он равняется значению два. Это и будет стационарная точка, которая будет попадать в отрезок

Определяем значения на концах отрезка, в данной точке.

А именно: x=1, x=2, x=4.

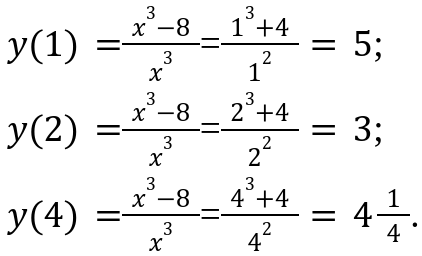
Мы определили максимальное значение, которое можно записать в следующем виде max y=y(2)=3. Данная запись будет актуальна, при x=1, минимальное значение min y=y(2)=3 — когда х=2.

Что касаемо второго отрезка, то ни одно стационарной точки, он в себя не включает. Поэтому вычисляем значения на концах заданного отрезка.

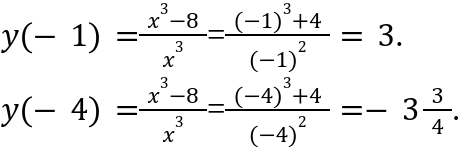
Следовательно: максимальное значение будет равняться трем, а минимальное будет равно — \.

Четность и нечетность функции

Определение 2

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться

График этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

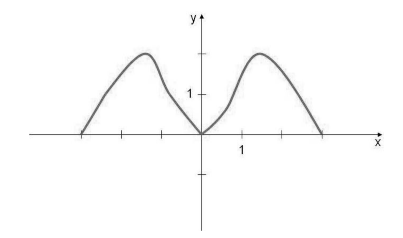Рисунок 1.

Статья: Общие свойства функций и построение графиков

Найди решение своей задачи среди 1 000 000 ответов

Определение 3

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться

График этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

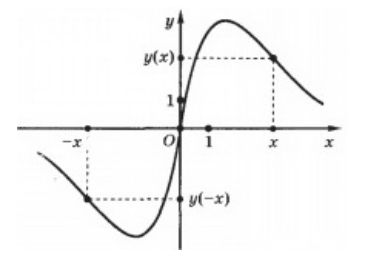Рисунок 2.

Для исследования функции в её аналитической записи заменяют переменную $x$ на переменную $-x$, производят, при необходимости элементарные преобразования, и проверяют условия определений 2 и 3.

Периодические функции.

Число $T\neq 0$ называют периодом функции $f$, если для любого $x\in D(f)$ значения $x+T$ и $x-T$ также принадлежат $D(f)$ и выполняется равенство
$$
f(x-T)=f(x)=f(x+T).\nonumber
$$
Функцию, имеющую период $T$, называют периодической с периодом $Т$.

Отметим, что если $T$ — период функции $f$, то каждое число вида $nT$, где $n\in\mathbb{Z},\;n\neq 0$, также является периодом этой функции.

Примерами периодических функций могут служить тригонометрические функции. При этом число $2\pi$ — наименьший положительный период функций $\sin x,\;\cos x,$ a $\pi$ — наименьший положительный период функций tg x и ctg x.

Пример 10

Доказать, что функция $f(x)=\sin\alpha x$, где $\alpha>0$ является периодической, и найти ее наименьший положительный период.

$\triangle$ Предположим, что $f$ — периодическая с положительным периодом T функция. Тогда для любых $x\in\mathbb{R}$ должно выполняться равенство
$$
\sin\alpha x=\sin\alpha (x+T),\label{ref7}
$$
откуда при х = 0 получаем
$$
\sin\alpha T=0,\ T=\frac{k\pi}{\alpha},\nonumber
$$
где $k\in\mathbb{N}$.

Таким образом, положительными периодами функции $\sin\alpha x$ могут быть только числа $k\pi/\alpha$, где $k\in\mathbb{N}$. Заметим, что число $\displaystyle \pi/\alpha$ не является периодом функции $\sin\alpha x$, так как в противном случае при всех $x\in\mathbb{R}$ выполнялось бы равенство $\displaystyle \sin\alpha x=\sin\alpha(x+\pi/\alpha)=\sin(\pi+\alpha x)=-\sin\alpha x$, то есть $\sin\alpha x=0$, что невозможно.

Число $\displaystyle 2\pi/\alpha$ — период функции $\sin \alpha x$, так как при любых $x\in\mathbb{R}$ справедливо равенство $\sin \alpha x=\displaystyle \sin \alpha(x+2\pi/\alpha)$.

Таким образом $2\pi/\alpha$ — наименьший положительный период функции $\sin\alpha x.\quad \blacktriangle$

Максимальные и минимальные значения функций на открытом и бесконечном значении интервала

Перед тем как начать разбирать новый способ, нужно вспомнить и повторить, как правильно определяются пределы односторонних значений и пределы значений бесконечности. А также вспомнить главные методы их вычисления.

Провести проверку, чтобы заданный интервал значений подходил под необходимую область значения функции;
Определиться со всеми нужными точками, которые находятся в заданном интервале. И где отсутствует первая производная значения. Обычно это у функций, где аргумент является в знаке модуля. Функции со степенью, с дробно рациональным показателем.
Затем будем определять, постоянные точки, относящиеся в конкретный заданный промежуток. Значение производной, нужно приравнять к 0. Для этого решаем уравнение и подбираем необходимые корни значений. Если отсутствует стационарная точка или она не подходит под заданный интервал, значит переходим к следующему шагу. Его характеризует интервальный вид. Когда интервал выглядит как: ;

Когда интервал задается как значения (a;b], то нам надо вычислить значение функции в точке x = b и односторонний предел \.

Заданный интервал ( a ; b ), нужно вычислить пределы \ и \;

Если задан промежуток: ;

Когда значение интеграла задается как промежуток: (-∞; b], вычисляем значение в точке x = b и предел на минус бесконечности \;

Если ( − ∞ ; b ), то считаем односторонний предел \ и предел на минус бесконечности \;

Если же ( − ∞ ; + ∞ ), то считаем пределы на минус и плюс бесконечности \, \.

В заключении необходимо сделать вывод на основании расчета по вычислению необходимых значений и промежутков функции. Это подразумевает несколько вариантов. Когда предел с одной стороной равен отрицательной бесконечности или плюс бесконечности. Становится очевидно, что о минимальном и максимальном значении функции ничего конкретного сказать нельзя. При его решении мы будем руководствоваться алгоритмом решения, приведённым выше по тексту.

По заданию нам дана задача, в которой указана функция.

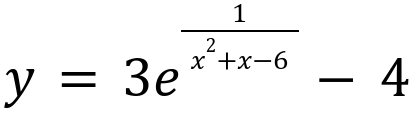
По условию необходимо определить минимальные и максимальные значения в интервалах. А именно: ( − ∞;-4), (-∞; -3), (-3; 1], (-3; 2), [1;2), (2; +∞); [4;+∞).

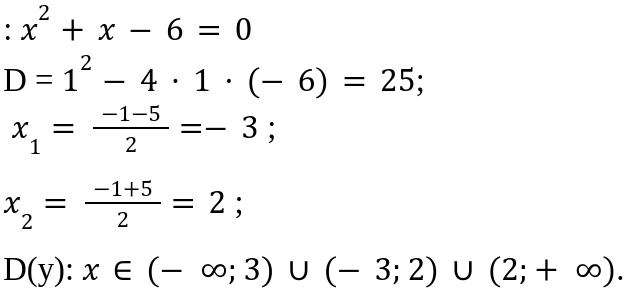
Затем выполним дифференцированный расчет функции и вычислим следующие данные:

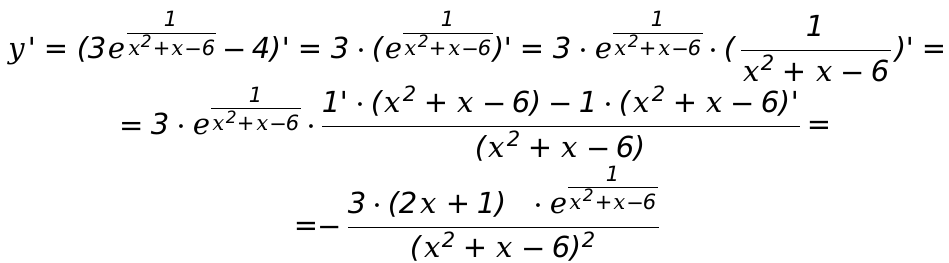
Следовательно, производные могут существовать на всей области. Определим значения стационарных значений точек. Производная функции равняется 0 при x = \. Это точка, принадлежит интервалу значений ( − 3 ; 1 ] и (-3;2).

Подставим в функцию и вычислим значение при x = − 4 для заданного промежутка ( − ∞ ; − 4 ].

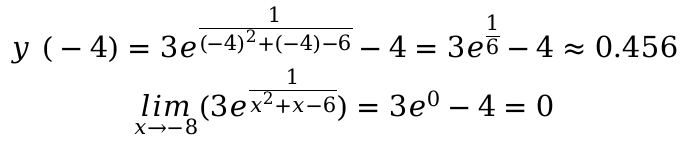
Так как \, максимальное значение \

Данная ситуация не дает возможности вычислить самое минимальное значение. Есть возможность, только сделать вывод, что в нижней части функции есть ограничение до -1. Так как к этому значению функция непосредственно приближается постоянно на значение бесконечности с отрицательным показателем. Признак второго интервала, там отсутствуют стационарные точки и границы предела. Поэтому выполнить вычисление максимум и минимум точек не представляется возможным.

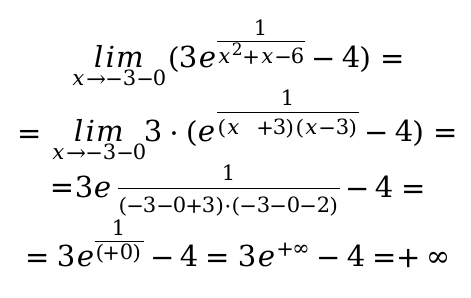
Чтобы подсчитать максимальное числовое значение заданной функции для третьего промежутка. Нужно вычислить ее значения в точке x = − 1 /2, при заданном значении x = 1. Также определяем односторонний предел в конкретной ситуации для точки, когда аргумент функции имеет стремление к − 3 с положительной стороны по значению:

Следовательно \, а минимальное значение вычислить нет возможности. Функция ограничена снизу числовым значение равным (− 4). Следовательно, значения, которые у нас получились в предыдущих расчетах, на промежутке значений [ 1 ; 2 ) максимальное значение, функция будет принимать при x = 1. Вычислить наименьшее значение по математическим законам не возможно. На промежутке ( 2 ; + ∞ ) функция не может достигнуть максимального, а также и минимального значения. Так как функция принимает данные из интервала ( − 1 ; + ∞ ).

Область определения и ее характеристика

Функция задается тогда, когда любому значению, например x соответствует любое y. Независимой переменной называют значение х или по-другому аргументом. Числовое значение y, как правило, является зависимой переменной.

Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)

Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.

Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.

Область ограничения действительных чисел может быть от \.

Например: [5,7).

Область определения может указывать на следующие характеристики:

деление функции как \;
корень четной степени и переменная под корнем:

\{2^{2 \cdot x+1}}\];

переменная в основании степенного значения \
логарифмическая переменная \. Значения основания должно быть положительным.
Также, как и логарифмическое значение.
переменная тангенса и котангенса в виде следующего уравнения: \.

Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.

Пример 1: \, в данном множестве нет переменной, поэтому и решается оно иначе.

Пример 2: \, нужно вычислить область определения

Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено

Следовательно получаем следующее действие: \.

Область не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах \.

Ограниченные и неограниченные функции.

Функцию f называют ограниченной снизу на множестве $X\subset D(f)$, если существует число $С_1$ такое, что для любого $x\in X$ выполняется неравенство $f(x) \geq C_1$.

Используя символы $\exists$ и $\forall$, это определение можно записать так:
$$
\exists C_{1}:\forall x\in X\rightarrow f(x)\geq C_{1}.\nonumber
$$
Аналогично функцию f называют ограниченной сверху на множестве $X\subset D(f)$, если
$$
\exists C_{2}:\forall x\in X\rightarrow f(x)\leq C_{2}.\nonumber
$$

Функцию, ограниченную и сверху, и снизу на множестве X, называют ограниченной на этом множестве.

Функция f является ограниченной на множестве X тогда и только тогда, когда
$$
\exists c>0:\forall x\in X\rightarrow|f(x)|\leq C.\label{ref4}
$$

Если неравенство $|f(x)|\leq C$ выполняется для всех $x\in D(f)$, говорят, что функция f ограничена.

Геометрически ограниченность функции f на множестве X означает, что график функции $y=f(x), x\in X,$ лежит в полосе ${-C\leq y\leq C}.$

Например, функция $y=\displaystyle \sin\frac{1}{x}$, определенная при $x\in\mathbb{R}, x\neq 0$, ограничена, так как
$$
|\sin\frac{1}{x}|\leq 1\nonumber
$$

Функция f не ограничена на множестве X, если условие \eqref{ref4} не выполняется, то есть
$$
\forall C>0\ \exists x_{C}\in X:|f(x_{C})|\geq C.\label{ref5}
$$

Если $X= D(f)$ и выполнено условие \eqref{ref5}, то говорят, что функция f не ограничена.

Пример 8

Доказать, что функция $y=\displaystyle \frac{1}{x^{2}}$ не ограничена.

$\triangle$ Функция $\displaystyle \frac{1}{x^{2}}$ определена при $x\in\mathbb{R}$, $x\neq 0$. Пусть C — любое положительное число, и пусть $\displaystyle {x_{C}=\frac{1}{\sqrt{2C}}}$, тогда $\displaystyle y(x_{C})=2C>C$ то есть выполняется условие \eqref{ref5}. $\blacktriangle$

Пусть Y — множество значений, которые функция f принимает на множестве $X\subset D(f)$ . Тогда точную верхнюю грань множества Y называют точной верхней гранью функции f на множестве X и обозначают $\sup_{x\in X}{f(x)}$, а точную нижнюю грань множества Y — точной нижней гранью функции f на множестве X и обозначают $\displaystyle \inf_{x\in X}{f(x)}$.
Если X=D(f), то в этих определениях указание на множество X опускают.

Пусть существует точка $x_{0}\in X\subset D(f)$ такая, что для всех $x\in X$ выполняется неравенстве $f(x) \leq f(x_0)$.Тогда говорят, что функция f принимает в точке $x_{0}$ наибольшее (максимальное) значение на множестве X и пишут $f(x_{0})=\displaystyle \max_{x\in X}f(x)$ В этом случае $\displaystyle \sup_{x\in X}{f(x)}=f(x_{0}) $

Аналогично, если $\exists x_{0}\in X\subset D(f):\forall x\in X\rightarrow f(x)\geq f(x_{0})$ , то говорят, что функция f принимает в точке $x_0$ наименьшее (минимальное) значение на множестве X, и пишут $f(x_{0})=\displaystyle \min_{x\in X}f(x)$. В этом случае $\displaystyle \inf_{x\in X}f(x)=f(x_{0})$.

Максимальные и минимальные значения называют экстремальными.

Например, если $f(x)=\sin x$, то $\displaystyle \sup_{x\in\mathbb{R}}f(x)=\max_{x\in\mathbb{R}}f(x)=f(x_{k})$, где $x_{k}=\displaystyle \frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z},\;\inf_{x\in\mathbb{R}}f(x)=\min_{x\in\mathbb{R}}{f}(x)=f(\widetilde{x}_{k}),$ где $\widetilde{x}_{k}=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z}$.

Пример решения

Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:

Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.

Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.

Условие достаточности для возрастания и убывания функции

Исходя из условия достаточных признаков увеличения и уменьшения функции определяются пределы возрастания и убывания функции.

Основные определения характеристик возрастания и убывания функции на заданном интервальном промежутке:

когда значение производной функции, имеют следующий вид: y=f(x) является положительной для каждого значения x из заданного промежутка X, тогда значение функции будет возрастать на X;
когда производная функции отрицательна y=f(x) при любом значении x из интервала значений X, следовательно, функция будет иметь убывающий вид.

Для того, чтобы определить промежутки, на которых будет возрастать и убывать функция, нужно выполнить следующие условия:

определить значение производной для функции;
найти значение неравенства \ на заданной области определения;
к найденным значениям промежуток нужно прибавить точки, которые расположены в начале и в конце границы. И функция имеет положение определенной и непрерывной.

Пример №1:

Необходимо найти промежутки возрастания и убывания значения функции, используя алгоритм решения.

Задана функция: \

Определим область значения данной функции.

Для нашего примера, обязательно условие: знаменатель не должен равняться нулю. Поэтому \

Определяем значение производной функции:

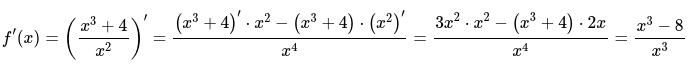
Вычисляем необходимые промежутки, где функция возрастает и убывает функции по признаку достаточности и решаем следующее неравенство: \ на области определения.

Для решения нужно воспользоваться методом интервалов. Единственным подкоренным значение для числителя является значение x = 2. При этом знаменатель преобразуется в нулевое значение и x=0.Данные точки делит область определения на промежутки, в которых значение производной функции сохраняет свой первоначальный знак.

Все точки на числовой прямой отмечаются. Плюс и минус — это интервал, где производная имеет положительное значение и отрицательное соответственно.

Нижние стрелки отражают возрастание или убывание функции на заданном соответствующем интервале значений.

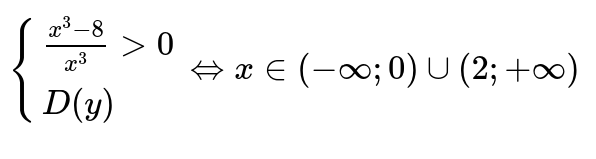
Следовательно:

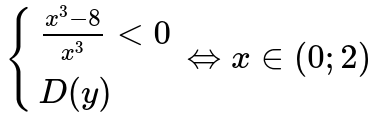
В определенной точке равной x=2 функция определена и является непрерывной. Ее следует отнести к промежутку, где функция возрастает и убывает.

В точке со значением x=0 функция не определена. Поэтому ее нужно полностью исключить из промежутка.

Изобразим график функции для отражения полученных в процессе вычислений значений.

Ответ: Заданная функция будет возрастать при следующих значениях \ и убывать на интервале (0;2].

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Обратная функция.

Пусть задана числовая функция $y=f(x),\;x\in D(f)$. Тогда каждому числу $x_0\in D(f)$соответствует единственное число $y_{0}=f(x_{0})\in E(f)$ . Нередко приходится по заданному значению функции $y_0$ находить соответствующее значение аргумента, то есть решать относительно $x$ уравнение
$$
f(x)=y_{0},\quad y_{0}\in E(f).\label{ref8}
$$

Это уравнение может иметь не одно, а несколько и даже бесконечно много решений. Решениями уравнения \eqref{ref8} являются абсциссы всех точек, в которых прямая $y=y_0$ пересекает график функции $y=f(x)$.

Например, если $f(x)=x^{2}$, то уравнение
$$
x^{2}=y_{0},\quad y_{0}>0,\nonumber
$$
имеет два решения: $x_{0}=\displaystyle \sqrt{y_0}$ и ${\widetilde x}_0=\sqrt{y_0}$. Если $f(x)=\sin x$, то уравнение
$$
\sin{x}=y_{0},\quad |y_{0}|\leq 1,\nonumber
$$
имеет бесконечно много решений вида $x_n=(-1)^{n}x_{0}+\pi n$, где $n\in\mathbb{Z}\;x_0$ — одно из решений этого уравнения.

Однако существуют функции, для которых уравнение \eqref{ref8} при каждом $y_{0}\in E(f)$ однозначно разрешимо, то есть имеет единственное решение $x_0\in D(f)$. Этим свойством обладают, например, следующие функции:

$f(x)=3x+4,\;D(f)=\mathbb{R}$;
$f(x)=x^{3},\;D(f)=\mathbb{R}$;
$f(x)=\displaystyle \frac{1}{x},\quad D(f)=\{x\in\mathbb{R},\;x\neq 0\}$.

Если функция $f$ такова, что при каждое значение $y_{0}\in E(f)$ она принимает только при одном значении $x_{0}\in D(f)$ , то эту функцию называют обратимой. Для такой функции уравнение
$$
f(x)=y\nonumber
$$
можно при любом $у\in Е(f)$однозначно разрешить относительно $x$, то есть каждому $y\in Е(f)$ соответствует единственное значение $x\in D(f)$.

Это соответствие определяет функцию, которую называют обратной к функции $f$ и обозначают символом $f^{-1}$.

Заметим, что прямая $y=y_0$ для каждого $y_{0}\in E(f)$ пересекает график обратимой функции $y=f(x)$ в единственной точке $(x_0,\;y_0)$, где $f(x_{0})=y_{0}$.

Обозначая, как обычно, аргумент обратной функции буквой $x$, а ее значения — буквой $y$, обратную для $f$ функцию записывают в виде
$$
y=f^{-1}(x),\quad x\in D(f^{-1}).\nonumber
$$

Для упрощения записи вместо символа $f^{-1}$ будем употреблять букву $g$.

Отметим следующие свойства, которые показывают, как связаны данная функция и обратная к ней:

если $g$ — функция, обратная к $f$, то и $f$ — функция, обратная к $g$; при этом
$$
D(g)=E(f),\quad E(g)=D(f),\nonumber
$$
то есть область определения функции $g$ совпадает с множеством значений функции $f$ и наоборот;
для любого $x\in D(f)$ справедливо равенство
$$
g(f(x))=x,\nonumber
$$
а для любого $х\in Е(f)$ справедливо равенство
$$
f(g(x))=x;\nonumber
$$
график функции $y=g(x)$ симметричен графику функции $y=f(x)$ относительно прямой $y=x$;
если нечетная функция обратима, то обратная к ней функция также является нечетной;
если $f$ — строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция $g$ также является строго возрастающей (строго убывающей).

Рис. 9.9

Свойства 1) и 2) следуют непосредственно из определения обратной функции, 4) и 5) — из определений обратной и соответственно нечетной и строго монотонной функции.

Рис. 9.10

Рассмотрим свойство 3). Пусть точка $(x_{0},y_{0})$ принадлежит графику функции $y=f(x)$, то есть $y_{0}=f(x_0)$. Тогда $x_{0}=g(y_{0})$, то есть точка $(x_{0},y_{0})$ принадлежит графику обратной функции $g$. Так как точки $(x_{0},y_{0})$ и $(y_{0},x_{0})$ симметричны относительно прямой $y=x$ (рис. 9.9), то график функции $у=g(х)$ симметричен графику функции относительно этой прямой.

Рис. 9.11

На рис. 9.10 изображены графики взаимно обратных функций $y=x^{2},\;x\geq 0$, и $y=\sqrt{x}$, а на рис. 9.11 — графики взаимно обратных функций $y=x^{2},\;x\leq 0$, и $y=-\sqrt{x}$.

Неявные функции. Параметрически заданные функции.

Пусть Е — множество точек $M(x,y)$ плоскости $Oxy$. Если каждой точке $M\in E$ поставлено в соответствие по некоторому правилу (закону) число z, то говорят, что на множестве E задана числовая функция от переменных $x$ и $y$, и пишут $z=f(x,y),\;(x,y)\in E$.

Например, объем конуса $v$ есть функция от переменных r и h, где r — радиус основания, h — высота конуса. Эта функция задается формулой $v=\displaystyle \frac{1}{3}\pi r^{2}h$.

Аналогично вводится понятие функции от трех и большего числа переменных.

Пусть функция $F(x,y)$ определена на некотором множестве точек плоскости. Рассмотрим уравнение
$$
F(x,y)=0.\label{ref9}
$$

Рис. 9.12

Графиком уравнения \eqref{ref9} в прямоугольной системе координат называют множество всех точек плоскости, координаты которых удовлетворяют этому уравнению. Например, графиком уравнения
$$
x^{2}+y^{2}-1=0\label{ref10}
$$
является единичная окружность (рис. 9.12).

Естественной является постановка вопроса о том, можно ли уравнение \eqref{ref9} однозначно разрешить относительно $y$, то есть найти единственную функцию $y=f(x)$ такую, что $F(x,f(x))=0$, где $x$ принимает значения из некоторого промежутка.

Обратимся к уравнению \eqref{ref10}. Если $|x|>1$, то не существует значений $y$ таких, что пара чисел $(x,y)$ удовлетворяет уравнению \eqref{ref10}. Если $|x|\leq 1$, то, решая это уравнение относительно y, получаем
$$
y=\pm\sqrt{1-x^{2}}.\label{ref11}
$$

Таким образом, если $|x|\;<1$, то из уравнения \eqref{ref10} $y$ выражается через $х$ неоднозначно: каждому значению $x$ соответствуют два различных значения $y$, а именно $y_{1}=-\sqrt{1-x^{2}}\quad y_{2}=\sqrt{1-x^{2}}\quad (y_{1}=y_{2}$ при $x=-1\;x=1)$.

Отсюда следует, что всякая функция $y=f(x)$, которая в точке $x\in$ принимает либо значение $y_{1}$, либо значение $y_{2}$, удовлетворяет уравнению \eqref{ref10}, то есть
$$
x^{2}+f^{2}(x)-1=0,\quad x\in.\nonumber
$$

Например, функция $y=f(x)$, принимающая значение $y_1$ при $x\in$, удовлетворяет уравнению \eqref{ref10}. Меняя $\alpha$, можно получить бесконечное множество функций, удовлетворяющих на отрезке  уравнению \eqref{ref10}.

Будем теперь рассматривать уравнение \eqref{ref10} в прямоугольнике
$$
K_{1}=\{(x,y):-1\leq x\leq 1,\;0\leq y\leq 1\}.\nonumber
$$

В этом случае существует единственная функция $y=y_{1}=\sqrt{1-x^{2}},\;-1\leq x\leq 1$, удовлетворяющая уравнению \eqref{ref10} и такая, что $y\in$. Эту функцию называют неявной функцией, определяемой уравнением \eqref{ref10} в прямоугольнике $K_1$.

Аналогично в прямоугольнике $K_{1}=\{(x,y):-1\leq x\leq 1,\;-1\leq y\leq 0\}$ неявная функция, определяемая уравнением \eqref{ref10}, задается формулой $y=y_{2}=-\sqrt{1-x^{2}},\;-1\leq x\leq 1$.

Вернемся к уравнению \eqref{ref9}. Пусть прямоугольник $K=\{(x,y):|x-x_{0}|\leq a,\;|y-у_0|\leq b$ содержится в области определения функции $F(х,у)$, и пусть $F(х_0,y_0)=0$. Если на отрезке $\Delta=\lceil x_{0}-a,x_{0}+a\rceil$ существует единственная функция $y=f(x)$ такая, что $f(x)\in\lceil y_0-b,y_0+b\rceil$ и
$$
F(x,f(x))=0,\quad x\in\Delta,\nonumber
$$
то говорят, что уравнение \eqref{ref9} определяет в прямоугольнике $K$ переменную y как неявную функцию переменной $x$.

Достаточные условия существования неявной функции и другие вопросы, связанные с неявными функциями, рассматриваются далее в параграфе 28.

Функция одной переменной может быть задана не только в явном виде $y=f(x)$ или неявно уравнением $F(х,у)=0$, но также параметрически. Этот способ задания состоит в следующем.

Пусть функции $x=\varphi(t)$ и $\varphi(t)$ определены на некотором множестве $E$, и пусть $E_1$ — множество значений функции $\varphi$. Предположим, что функция $\varphi$ обратима на множестве $E$, и пусть $t=\varphi^{-1}(x)$ — обратная к ней функция. Тогда на множестве $E_1$ определена сложная функция $y=\psi(\varphi^{-1}(x))=f(x)$, которую называют параметрически заданной формулами (уравнениями) $х=\varphi(t),\quad y=\psi(t)$.

Например, уравнениях $x=\cos t,\;y=\sin t$, где $t\in\left $, определяют параметрически заданную функцию $y=f(x)$. В данном случае $t=\arccos x,\;y=\sin(\arccos x)=\sqrt{1-x^{2}}$.