Квадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4×2 + 6xy + 6xy + 9y2 = 4×2 + 12xy + 9y2
То есть выражение (2x + 3y)2 равно 4×2 + 12xy + 9y2
(2x + 3y)2 = 4×2 + 12xy + 9y2
Решим аналогичный пример, который попроще:
(a + b)2
Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)
(a + b)2 = (a + b)(a + b)
Выполним это умножение:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
То есть выражение (a + b)2 равно a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
a = 2x
b = 3y
И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4×2 + 12xy + 9y2
Как и в прошлый раз получили многочлен 4×2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x + 3y)2 = 4×2 + 12xy + 9y2
Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3)2 = 52 = 25
Второй способ:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
Значит, (5a + 3)2 = 25a2 + 30a + 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b
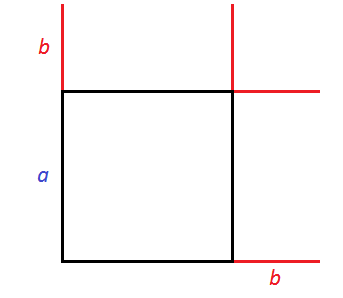
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
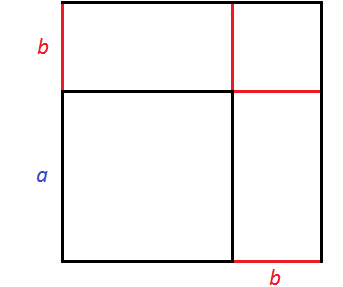
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b
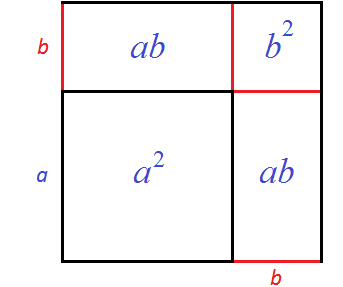
В результате получается следующая сумма площадей:
a2 + ab + ab + b2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Способ 1: построение треугольника Паскаля по предыдущей строке
Этапы этой процедуры такие же, как и в треугольнике Паскаля. Допустим, мы хотим создать треугольник Паскаля до семи рядов.
Шаги для достижения этого следующие:
Шаг 1) Начните самую верхнюю строку с «1».
Шаг 2) Для строки «r», элемент «c» будет произведением «c-1» и «c» — номера строки «r-1».
Шаг 3) Первый и последний numbers подряд всегда будет «1».
Мы должны придерживаться этих трех простых шагов, чтобы создать треугольник Паскаля.
Код C++ треугольника Паскаля по предыдущей строке
#include <bits/stdc++.h>
using namespace std;
void printRow(int n)
{
int numbers;
for (int row = 0; row < n; row++)
{
for (int col = 0; col <= row; col++)
{
if (col == 0 || col == row)
{
numbers = 1;
}
else
{
numbers = numbers + numbers;
}
cout << numbers << "\t";
}
cout << endl;
}
}
int main()
{
int n;
cout << "How many rows: ";
cin >> n;
printRow(n);
}
Вывод:
How many rows: 7 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1
Код Python формулы треугольника Паскаля по предыдущей строке
def printRow(n):
numbers =
for col in range(n)
]
for row in range(len(numbers)):
for col in range(0, row+1):
if row == col or col == 0:
numbers = 1
else:
numbers = numbers+numbers
print(numbers,end="\t")
print("\n")
n = int(input("How many rows: "))
printRow(n)
Вывод примера треугольника Паскаля:
How many rows: 7 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1
сplexАнализ города
A двумерный массив был использован при реализации. Учитывая, что N — количество строк в треугольнике Паскаля. Для этого потребуется Н.2 единичные помещения. Следовательно, O будет пространством com.plexитность (N2).
У нас есть два цикла в функции, и каждый цикл выполняется «N» раз. Итак, время комplexэто тоже НА2) или квадрат времени complexность.
История открытия

Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.

Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Задания для самостоятельного решения
Задание 1. Преобразуйте выражение (m + n)2 в многочлен.
Решение:
(m + n)2 = m2 + 2mn + n2
Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.
Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64
Задание 3. Преобразуйте выражение (2×2 + 3×3)2 в многочлен.
Решение:
(2×2 + 3×3)2 = (2×2)2 + 2 × 2×2 × 3×3 + (3×3)2 = 4×4 + 12×5 + 9×6
Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.
Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25
Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.
Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2
Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.
Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625
Задание 7. Преобразуйте выражение (3×2 − y3)2 в многочлен.
Решение:
(3×2 − y3)2 = (3×2)2 − 2 × 3×2 × y3 + ( y3)2 = 9×4 − 6x2y3 + y6
Задание 8. Выполните умножение (x − y)(x + y)
Решение:
(x − y)(x + y) = x2 − y2
Задание 9. Выполните умножение (2x − y)(2x + y)
Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4×2 − y2
Задание 10. Выполните умножение (7 + 3y)(3y − 7)
Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49
Задание 11. Выполните умножение (x2 − 5)(x2 + 5)
Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25
Задание 12. Выполните умножение (a3 − b2)(a3 + b2)
Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4
Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)
Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6
Задание 14. Выполните умножение (9x − y2)(y2 + 9x)
Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81×2 − y4
Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)
Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3
Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)
Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19
Задание 17. Выполните умножение (4x + 1)(16×2 − 4x + 1)
Решение:
(4x + 1)(16×2 − 4x + 1) = (4x)3 + 13 = 64×3 + 1
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Как запомнить формулы сокращенного умножения?
Самый простой способ запомнить ФСУ – это выучить их названия. Например, у нас есть формула (a + b)2, т.е. квадрат скобок, а в скобках у нас сумма, и это значит, что данное выражение называется квадратом суммы (точно так же, как квадрат разности, если в скобках стоит знак «–»). По аналогии, (a + b)3 и (a – b)3 будут называться кубом суммы и кубом разности.
Если же мы имеем выражение a2 – b2, где оба выражения в квадрате, это будет разностью квадратов. И точно так же можно запомнить, что такое разность и сумма кубов и т.д.
Но как же запомнить сами формулы? Здесь на помощь приходят механическая память и несколько секретов запоминания. Например, нам нужно запомнить квадрат суммы (a + b)² = a² + 2ab + b². Смотреть на формулу и стараться ее «сфотографировать» – не очень эффективная стратегия. Лучше всего выучить формулу в ее словесной формулировке, а звучит она так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Словесные формулировки многократно улучшают запоминание ФСУ и пригождаются в самых разных ситуациях, когда приходится эти самые формулы вспоминать. Поэтому запомните и формулировки других формул:
- Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Запомнить эти формулировки при должном усердии достаточно просто. Но не возникло ли у вас сомнений в том, что все эти формулы верны? Если сомнения возникли, это вполне нормальное явление, ведь сомневаться всегда полезно. И несмотря на то, что данные ФСУ используются людьми уже много лет, давайте все же посмотрим на их доказательство.
Дополнительные формулы сокращенного умножения
Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.
Бином Ньютона
Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:

Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:
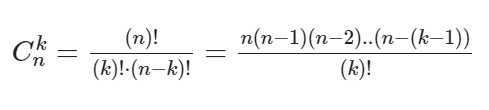
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.
Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Выглядит она так:

Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:
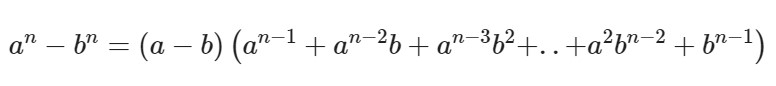
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.
Формула для четных показателей 2m:
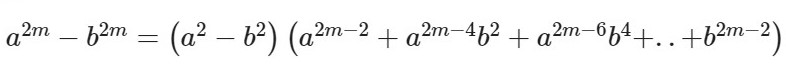
Формула для нечетных показателей 2m + 1:
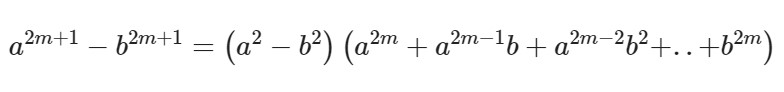
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.
Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.
Вопросы и ответы
И напоследок несколько ответов на часто задаваемые вопросы.
Для чего нужны формулы сокращенного умножения?
Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.
В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.
Как появились формулы сокращенного умножения?
Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.
Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.
Сколько всего формул сокращенного умножения?
Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.
Почему формулы сокращенного умножения изучают на алгебре в 7 классе?
Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.
Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.
Можно ли не использовать формулы сокращенного умножения?
Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.
Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.
Квадрат суммы и разности двух чисел
Рассмотрим формулы 1 и 2. Их можно объединить следующим образом:
(a \pm b)^2=a^2 \pm 2ab +b^2
Читается так:
Квадрат суммы (разности) двух чисел
Квадрат суммы (соответственно разности) двух чисел равен квадрату первого числа, плюс (минус) удвоенное произведение первого числа на второе, плюс квадрат второго числа.(a \pm b)^2=a^2 \pm 2ab +b^2
Примеры на квадрат суммы и разности двух чисел
Выполнить действия
- (x+2y)^2(x+2y)^2=x^2+2x (2y)+y^2=x^2+4xy+4y^2
- (m+n^2)^2(m+n^2)^2=m^2+2mn^2+n^4
- (m+n^2)^2(a^2+b^4)^2=a^4+2a^2b^4+b^8
Представить в виде квадрата двучлена следующие трехчлены.
- x^2+2x+1x^2+2x+1=(x+1)^2
- 4a^2+4ab+b^24a^2+4ab+b^2=(2a)^2+2\cdot (2a)\cdot b+b^2=(2a+b)^2
- m^6+2m^3n^4+n^8(m^3)^2+2 (m^3)(n^4)+(n^4)^2=(m^3+n^4)^2
Дополнить до полного квадрата двучлена следующие выражения:
- 4a^2+12ab+… Чтобы найти третье слагаемое — ориентируемся на второе слагаемое в котором выделяем корень квадратный из первого. То есть, второе слагаемое 12ab из него выделяем корень квадратный из первого слагаемого \sqrt{4a^2}=2a, остается 12ab :2a=6b. Но так как в формуле (a+b)^2=a^2+2ab+b^2 и во втором слагаемом мы видим удвоенное произведение первого слагаемого на второе, нужно еще разделить на 2. Первое слагаемое мы определили, это 2a, теперь от 6b убираем множитель 2 и остается третье слагаемое 3b. И мы получаем: 4a^2+12ab+…=(2a)^2+2\cdot (2a)\cdot (3b)+(3b)^2=4a^2+12ab+9b^2m^2-2mn+…
- m^2-2 \cdot m \cdot n+…=m^2-2\cdot m\cdot n+n^2
- 25x^2+ ? + 49b^225x^2+ ? + 49b^2=(5x)^2+?+(7b^2)=(5x)^2+2 (5x)(7b)+(7b)^2=25x^2+70xb+49b^2
Выделить квадрат суммы или разности:
- x^2+8xНам дан неполный квадрат суммы. Дополняя мы обычно либо выделяем какое то число или выражение, если нам не хватает до полного квадрата суммы или разности, или добавляем его, но тогда то же выражение надо и отнять.x^2+8x=x^2+2\cdot 4 \cdot x+(4)^2- (4)^2=(x+4)^2-16
- x^2-2x+3x^2-2x+3=x^2-2x+1+2=(x-1)^2+2
- x^2+6x-3x^2+6x-3=(x)^2+2 \cdot x \cdot 3+9-9-3=(x)^2+6x+9-12=(x+3)^2-12
Вычислите, используя формулы (a+b)^2=a^2+2ab+b^2 и (a-b)^2=a^2-2ab+b^2:
- 103^2103^2=(100+3)^2=100^2+2\cdot 100 \cdot 3+3^2=10000+600+9=10609
- 49^249^2=(50-1)^2=50^2-2\cdot 50\cdot 1+1^2=2500-100+1=2401
- 10,5^210,5^2=(10+0,5)^2=10^2+2\cdot 10 \cdot 0,5+0,5^2=100+10+0,25=110,25
- 99^299^2=(100-1)^2=100^2-2\cdot 100 \cdot 1+1=10000-200+1=9801
- 8,9^28,9^2=(9-0,1)^2=9^2-2\cdot 9 \cdot 0,1+0,1^2=81-1,8+0,01=79,2+0,01=79,21
Геометрия в пространстве (стереометрия)
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Тригонометрия
Пусть имеется прямоугольный
треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное
тригонометрическое тождество
Простейшие следствия из основного
тригонометрического тождества:
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы
преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы
преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для
синуса:
Формула понижения степени для
косинуса:
Формула понижения степени для
тангенса:
Формула понижения степени для
котангенса:
Формула половинного угла для
тангенса:
Формула половинного угла для
котангенса:
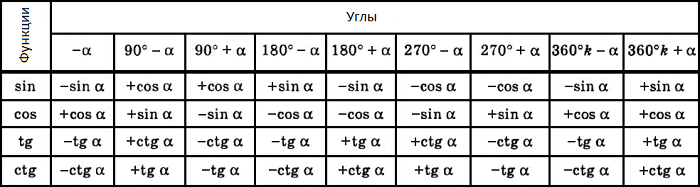
Тригонометрические формулы
приведения
Формулы
приведениязадаются
в виде таблицы:
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4×2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4×2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4×2 − 25
(2x − 5)(2x + 5) = 4×2 − 10x + 10x − 25 = 4×2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16×2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9×2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2) = −25×2 + 9y2
Примеры задач для 7−8 класса
В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре. Если вы новичек, то лучше всего начать играть без настоящих ставок. Однако если уже вы решились, то найти интернет казино вулкан с выводом на реальные деньги можно с помощью рейтингов или же обратившись за советом к более опытным гемблерам. В принципе можно попробовать метод проб и ошибок, но это будет сложнее и дольше.
Задача 1. Упростить выражение:
(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).
Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.
- (m + 3)² = m² + 6m + 9 (квадрат суммы),
- (3m + 1)(3m — 1) = 9m² 1 (разность квадратов),
- В последнем слагаемом необходимо выполнить перемножение: 2m (5m + 3) = 10m² + 6m.

Подставим полученные результаты в исходное выражение:
(m² + 6m + 9) + (9m² 1) — (10m² + 6m).
С учётом знаков раскроем скобки и приведём подобные слагаемые:
m² + 6m + 9 + 9m² 1 — 10m² 6m = 8.
Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:
k⁵ + 4k⁴ + 4k³ 4k² 4k = k³.
Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.
k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.
Из правой и из левой части выносится общий множитель (k² + 4k +4):
k³(k² + 4k + 4) = k (k² + 4k + 4).
Всё переносится в левую часть уравнения, чтобы в правой остался 0:
k³(k² + 4k + 4) — k (k² + 4k + 4) = 0.
Снова необходимо вынести общий множитель:
(k³ k)(k² + 4k + 4) = 0.
Из первого полученного сомножителя можно вынести k. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²:
k (k² 1)(k + 2)² = 0.
Использование формулы разности квадратов:
k (k — 1)(k + 1)(k + 2)² = 0.
Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:
- k = 0,
- k — 1 = 0, k = 1,
- k + 1 = 0, k = -1,
- (k + 2)² = 0, k = -2.
На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.
Формулы
Первые упоминания о ФСУ мы встречаем во времена древнегреческих математиков. Так, тождества встречаются в работах Евклида, известного автора работ, посвященных геометрии. В его “Началах» есть практическое обоснование и доказательство одного из тождеств ФСУ.Вот так выглядят все ФСУ:
- a2 — b2 = (a + b)(a — b)
- (a + b)2 = a2 + 2ab + b2
- (a — b)2 = a2 — 2ab + b2
- a3 — b3 = (a — b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 — ab + b2)
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a — b)3 = a3 — 3a2b + 3ab2 — b3
Рассмотрим несколько примеров:
(a + b)2 = a2 + 2ab + b2
(a — b)2 = a2 — 2ab + b2
Первая формулаВозьмем сначала первую формулу. Что такое (a + b)2 ? Это выражение (а+b), умноженное само на себя:
(а+b)(а+b)
Дальше весь вывод состоит, фактически, в простом раскрытии скобок:
(а + b)(а + b)= a2 + аb + аb + b2
Приглядевшись к тому , что у нас получилось, мы заметим, что аb встречается два раза. Теперь осуществим задачу, которая называется приведением подобных членов. Напомним, что подобные члены — это переменные, которые встречаются в одном и том же выражении несколько раз:
a2 + ab + ab + b2 = a2 + 2ab + b2
Первая формула выведена. Теперь вторая:
(a — b)2=(a — b)(a — b)
Также, как и в первый раз, мы раскрываем скобки:
(a — b)(a — b)=a2 — ab — ab + b2=a2 — 2ab + b2
Запомнить очень просто, как оказывается на практике. При раскрытии скобок видно, что отличие первой от второй формулы в одном знаке, перед 2аb:
(a + b)(a — b)=a2 + ab — ab — b2=a2 — b2
Выражения ab и -ab сокращаются и остается тождество, которое у нас получилось.По такому же принципу решаются и формулы для кубов.
Выделение полного квадрата
Часто в многочлене второй степени содержится квадрат суммы или разности, но
содержится в скрытом виде. Чтобы получить полный квадрат в явном виде, нужно преобразовать
многочлен. Для этого, как правило, одно из слагаемых многочлена представляется в виде удвоенного
произведения, а затем к многочлену прибавляется и из него вычитается одно и то же число.
Пример 7. Рассмотрим многочлен второй степени
.
Решение. Этот многочлен можно преобразовать следующим образом:
Здесь мы представили
в виде удвоенного произведения на ,
прибавили к многочлену и вычли из него одно и то же число
, далее применили
формулу квадрата суммы для двучлена .
Итак, мы доказали равенство
,
показывающее, что многочлен второй степени
равен полному квадрату
плюс число .
Пример 8. Рассмотрим многочлен второй степени
.
Решение. Проведём над ним следующие преобразования:
.
Здесь мы представили
в виде удвоенного произведения на ,
прибавили к многочлену и вычли из него одно и то же число
, применили
формулу квадрата разности для двучлена .
Итак, мы доказали равенство
,
показывающее, что многочлен второй степени
равен полному квадрату
плюс число .
Квадрат разности
Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для \((a-b)^2\):
![]()
В более краткой записи имеем:
Квадрат разности: \((a-b)^2=a^2-2ab+b^2\)
Применяется она также, как и предыдущая.
Пример. Упростите выражение \((2a-3)^2-4(a^2-a)\) и найдите его значение при \(a=\frac{17}{8}\).
Решение:
|
\((2a-3)^2-4(a^2-a)=\) |
Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки. |
|
|
\(=4a^2-12a+9-4a^2+4a=\) |
Теперь приведем подобные слагаемые. |
|
|
\(=-8a+9=\) |
Вот теперь подставляем и наслаждаемся простотой вычислений. |
|
|
\(=-8·\frac{17}{8}+9=-17+9=8\) |
Пишем ответ. |
Ответ: \(8\).




























