Модуль

🔥 Видео

Уравнения с параметром. Алгебра, 8 классСкачать

Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Графический методСкачать

Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Решаем квадратное уравнение с параметромСкачать

Неравенства с модулем | Математика | TutorOnlineСкачать

✓ Параметр с модулями | ЕГЭ-2021. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

✓ Параметр с модулем и логарифмом | ЕГЭ. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

✓ Четыре способа решить параметр с модулем | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Уравнения с модулемСкачать

Задачи с параметром. Урок 17. Линейное уравнение с модулем. Графический метод решения.Скачать

#12. Крутое уравнение с параметром и модулем из ЕГЭ!Скачать

8 класс, 39 урок, Задачи с параметрамиСкачать

5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Профильный ЕГЭ 2023. Задача 17. Параметры. Методы решенияСкачать

Уравнения с параметром. Алгебра 7 класс.Скачать

Неравенства с модулем

Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам. 

Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0. 

Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 \(\rightarrow\) \(x = \frac{7}{3}\). 

Определим, с какими знаками модуль будет раскрываться на каждом промежутке. 

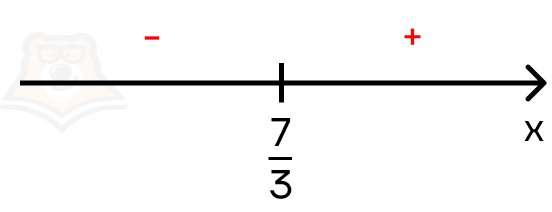
Осталось рассмотреть неравенство на двух промежутках. 

1. \(x \leq \frac{7}{3}\), тогдаx2 — (-(3x — 7)) + 7 >= 0x2 + 3x — 7 + 7 >= 0x2 + 3x >= 0x(x + 3) >= 0

Решим это неравенство «Методом интервалов». Сразу учтем ограничение \(x \leq \frac{7}{3}\). 

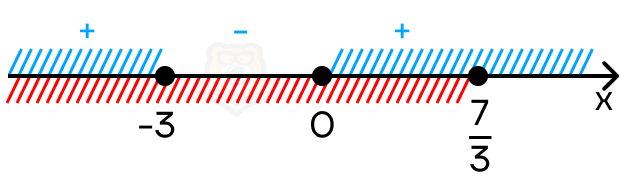
Получаем, что решением неравенства на заданном промежутке будет \(x \in (-\infty; -3] U\). 

2. \(x > \frac{7}{3}\), тогда x2 — 3x + 7 + 7 >= 0x2 — 3x + 14 >= 0x2 — 3x + 14 = 0D = 9 — 56 = -47 — корней на заданном отрезке не будет. 

Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0? Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график. Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.

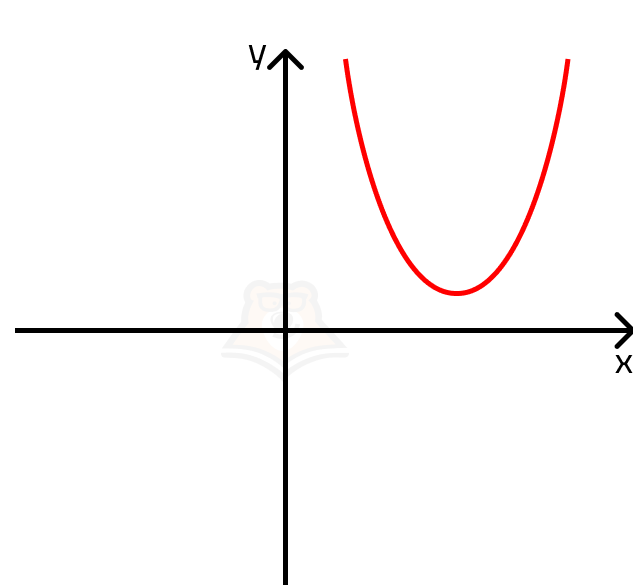
Однако не стоит забывать про ограничение \(x > \frac{7}{3}\). Накладывая его, получаем решение \((\frac{7}{3}; + \infty)\). 

Осталось только объединить полученные на промежутках решения: 

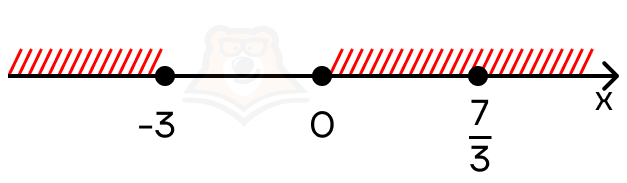
Получаем, что \(x \in (-\infty;- 3] U [0; +\infty)\).

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?

Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как: 

f(x) > a и -f(x) > a \(\rightarrow\) f(x) < -a. 

Отметим эти промежутки на числовой прямой:

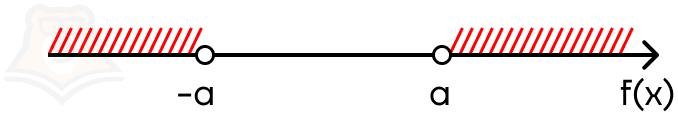
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности. 

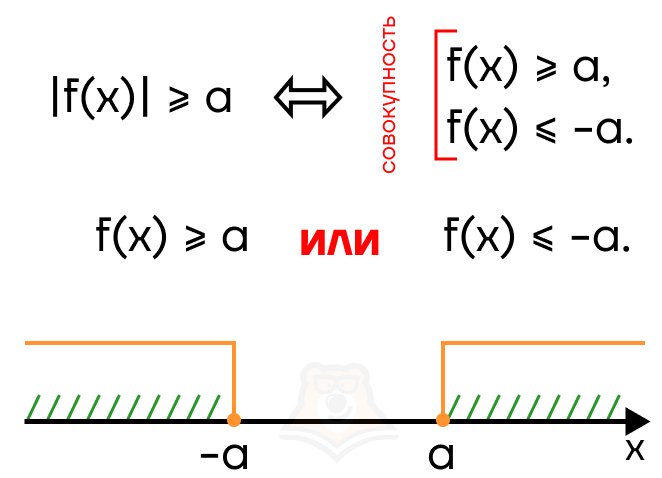
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a \(\rightarrow\) f(x) > -a. На числовой прямой это будет выглядеть следующим образом: 

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки. 

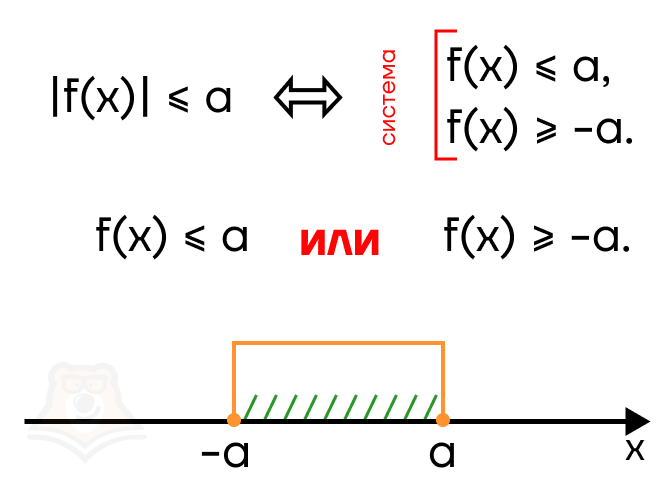
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат. 

|f(x)| ⋁ a | \(\uparrow\) 2 — вместо ⋁ может стоять любой знак неравенства. f2(x) ⋁ a2f2(x) — a2 ⋁ 0

Воспользуемся формулой сокращенного умножения:

(f(x) — a)(f(x) + a) ⋁ 0

Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0. 

Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:

|f(x)| ⋁ g(x) \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0  

g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат. 

|f(x)| ⋁ |g(x)| \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0

Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому. 

Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0. 

Решение. Перенесем модуль в другую часть неравенства:

|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно. 

Повторим действия, чтобы прийти к равносильному переходу:

(3x — 7)2 <= (x2+7)2(3x-7)2 — (x2 + 7)2 <= 0(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0(3x — 7 — x2 — 7)(3x + x2) <= 0(-x2 + 3x — 14) * x(3 + x) <= 0-(x2 — 3x + 14) * x(3 + x) <= 0(x2 — 3x + 14) * x(3 + x) <= 0

Рассмотрим первую скобку:

x2 — 3x + 14 = 0

D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:

x(3 + x) <= 0

Тогда \(x \in (-\infty;- 3] U [0; +\infty)\)

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

При решении можно сразу использовать равносильный переход, не расписывая его. 

Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.

Избавление от знака модуля

Пусть нам дано уравнение $\left| f\left(x \right) \right|=a$, причём $a\ge 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:

\

Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого

\

Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:

\

Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.

Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:

\

Опять раскрываем модуль с плюсом и минусом:

\

Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.

Решение уравнений с параметрами с помощью графиков.

Задача 1.

Найти все значения параметра q при которых уравнение

имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q2 − 8q + 13. Результат обозначим переменной а.
Т.е. примем и
решим уравнение с параметром

Строим график функции , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.
|x + 1| = 0; x = −1;
|x − 3| = 0; x = 3.

Вспомним:x

Таким образом на участке I, где −∞ < х ≤ −1, имеем

Следовательно, должны построить график функции . Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

На участке II, где −1 < х ≤ 3, имеем
и должны построить соответствующую часть графика функции .

На участке III, где 3 < х ≤ ∞, имеем

и должны построить соответствующую часть графика функции .

Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.

График функции представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

аy = −3−3 < y < 1y = 1аq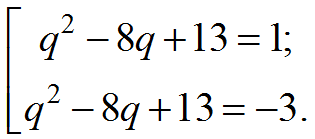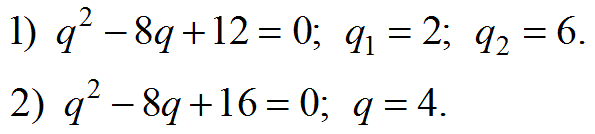ответ: {2;4;6}.

Задача 2.

Найти все значения параметра a, при которых уравнение

имеет ровно 3 корня.

Рассмотрим функцию . Видно, что если раскрыть скобки, то старший член будет −х3. Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

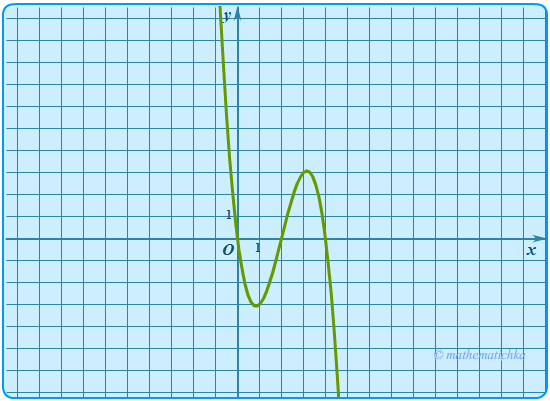
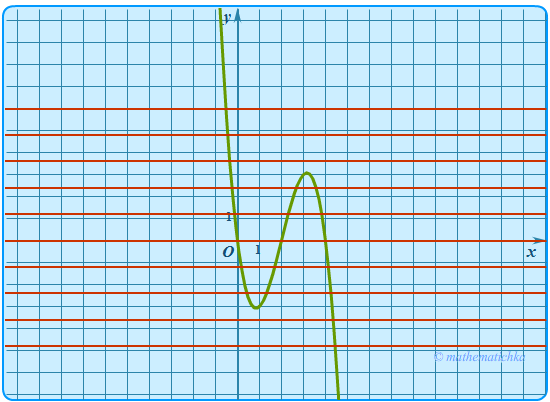
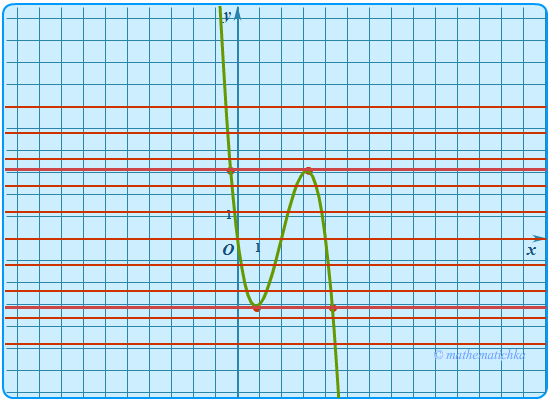
Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения ymax и ymin через производную

(Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют

Немного теории

Итак, поехали

Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $\left| -5 \right|=5$

Или $\left| -129,5 \right|=129,5$.

Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $\left| 5 \right|=5$; $\left| 129,5 \right|=129,5$ и т.д.

Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $\left| -5 \right|=\left| 5 \right|=5$; $\left| -129,5 \right|=\left| 129,5 \right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:

\

Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.

Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:

\

Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.

Таким образом, если рассмотреть функцию $y=\left| x \right|$ и попробовать нарисовать её график, то получится вот такая «галка»:

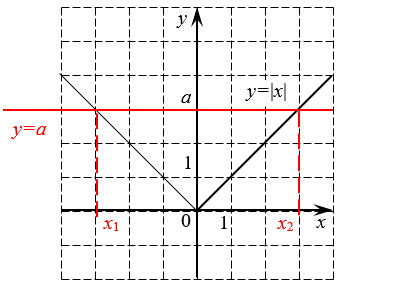График модуля и пример решения уравнения

Из этой картинки сразу видно, что $\left| -m \right|=\left| m \right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)

Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $\left| {{x}_{1}}-{{x}_{2}} \right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:

Модуль — это расстояние между точками на числовой прямой

Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

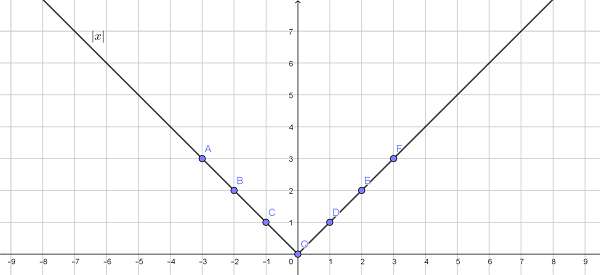
Объяснение: из рисунка видно, что график симметричен относительно оси Y.

Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

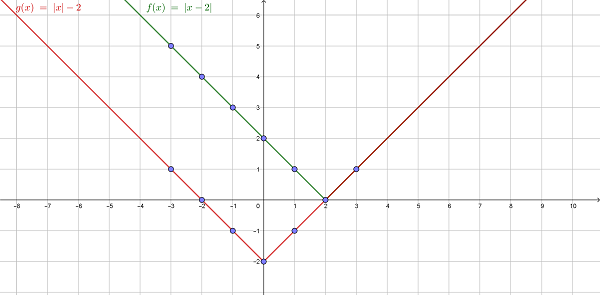
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Примеры решения задач с объяснением

Уравнения, которые содержат модуль и имеют вид |x| = |a|, решают с помощью определения модуля.

Воспользуемся стандартным алгоритмом:

Согласно первому свойству модуля:

, то есть модуль в любом случае не является отрицательным числом.

Можно обобщить рассмотренные действия и записать правило для решения уравнений, которые имеют вид |x| = a. Данное правило можно использовать в работе:

Далее рассмотрим решение уравнений, которые записаны в виде |x| = |y|.

При раскрытии модулей, согласно определению, возникнет необходимость во множестве проверок. Например, потребуется определить, какое число является положительным, а какое будет отрицательным. Полученную в результате систему в дальнейшем необходимо упростить.

Рассмотрим еще несколько примеров.

При решении уравнений с модулем также применяют метод интервалов. Данный способ следует применять в тех случаях, когда уравнение содержит более двух модулей.

Сложность заключается в том, что требуется проанализировать много вариантов, то есть по два варианта для каждого из модулей. Всего получится четыре уравнения. А в том случае, когда модулей три, потребуется рассмотреть восемь уравнений. Возникает необходимость в сокращении числа вариантов.

Заметим, что в нашем примере не предусмотрено одновременное выполнение всех условий:

Данные условия противоречивы относительно друг друга. В связи с этим, нецелесообразно раскрывать второй модуль со знаком плюс, когда первый модуль раскрыт со знаком минус. В результате получилось избавиться от одного уравнения.

Обобщая эту информацию, можно записать алгоритм действий. В первую очередь следует вычислить корни выражений, заключенных под знаком модуля. В результате получаются такие x, при которых выражения принимают нулевые значения:

С помощью стандартного способа интервалов можно отметить на координатной прямой корни выражений, которые находятся под модулями, и расставить знаки. Далее для каждого из полученных интервалов нужно составить и решить уравнение.

Первый интервал:

x < -3

В этом случае оба модуля раскрываются со знаком минус:

 является сторонним корнем.

Второй интервал:

В данном выражении первый модуль раскроется со знаком плюс, а второй — со знаком минус:

  полученный корень соответствует своему интервалу.

Третий интервал:

Теперь для обоих модулей будет записан знак плюс:

 данный корень также подходит для решения.

Выполним проверку корней. В первом случае корень посторонний:

Второй корень является решением:

Третий корень также является решением:

Таким образом, запишем ответ:

В этом случае следует раскрывать модули поочередно. Проанализируем два варианта решения.

Первое решение подразумевает вычисления для уравнения, которое имеет вид:

Тогда:

Здесь f(x) является подмодульным выражением. Применительно к нашей задаче, это:

Таким образом:

Получена пара простейших уравнений аналогичного вида, то есть:

Данные четыре числа являются решениями. Проверить это можно путем подстановки ответов в исходное уравнение.

Второй вариант решения является универсальным и позволяет справиться с нестандартными задачами.

Раскроем сначала внутренние модули:

Начальное уравнение будет записано, как пара уравнений:

Как решить уравнение с модулем икс

Давайте вместе с алгеброй применим логику. Логика позволяет нам делать некоторые предположения. Применительно к первоначальному уравнению, сделаем сразу 3 логических допущения.

1. Предположим, что х=0.
2. Допустим, что х>0.
3. Предположим, что х<0.

Этими тремя предположениями мы «перекрыли» весь диапазон возможных значений икс х, которые могут стать решением данного уравнения, так ведь? Значение х может быть нулевым, положительным или отрицательным.

Теперь давайте проверим каждое сделанное предположение. Выполним своеобразную «проверку гипотез» о том, что х может быть нулевым, положительным или отрицательным.

Икс равен нулю

Проверим первое предположение, что икс равен нулю (х=0):

Значит, первая гипотеза о том, что х = 0 оказывается не верна, поэтому отбросим ее.

Если в уравнении икс положительный

Проверим вторую гипотезу о том, что х является числом положительным. Тогда можно избавиться от знака модуля в исходном уравнении. Ведь если х является положительным числом, то |х| = х. Это очевидно, не так ли?!

Получим уравнение без знака модуля:

Итак, в результате решения нового уравнения, когда знак модуля был отброшен, получили ответ х = -1.

Однако в начале этой статьи мы получали такой же ответ, который не «проходил» элементарную проверку путем подстановки -1 в уравнение вместо х. Что не так?

Почему в результате решения уравнения мы получили х = -1, но проверка показывает неверный результат? Дело в том, что мы нарушили нашу собственную логику.

Второе предположение состояло в том, что значение х должно быть положительным (х>0). Но в результате подстановки положительного значения х в уравнение после его решения мы получили отрицательное значение х = -1.

А раз логика нарушена, значит наше предположение о том, что х является положительным числом НЕ ВЕРНО. Мы должны отбросить второе наше предположение, что х>0 так же, как мы отбросили первое предположение, что х=0.

Икс в уравнении отрицательный

Что же у нас остается? Остается третье логическое предположение, что значение х отрицательное (х<0). Давайте попробуем решить исходное уравнение при данном логическом предположении.

Итак, если х<0, то |х| = -х — это факт. Подставим в наше уравнение с модулем икс вместо |х| значение (-х). Тогда получим следующее:

Решаем полученное уравнение:

3х = -1, что означает х = -1/3.

Получается, если предположить, что х<0, решением уравнения будет значение х = -1/3, то есть отрицательное число «одна треть». Логика соблюдена? Да, конечно: мы предположили, мы построили гипотезу, что х<0, и в результате получили х = -1/3, мы получили отрицательное число, как и предположили. Значит, мы, действуя логически, наконец, решили уравнение.

Давайте на всякий случай проверим, действительно ли мы правы, решая исходное уравнение таким «замысловатым» логическим способом, делая предположения, гипотезы и затем их проверяя на логическую непротиворечивость:

2 * (-1/3) — |-1/3| = -2/3 — 1/3 = -3/3 = -1, что и требовалось получить в конечном итоге!

Вот что значит действовать логически при решении уравнения: делать логические предположения, далее пытаться решить уравнение на основе сделанных логических предположений. И в конце, после даже кажущегося удачного решения уравнения, проверять логическую непротиворечивость сделанных гипотез.

И тогда можно решать не только данное уравнение, являющееся не таким уж сложным, но и находить решения других более сложных задач.

Уравнения с модулем: примеры и достаточные знания, необходимые для решения заданий

Задания	Достаточные знания свойств	Формулы
$$\quad $$ $$x^2 — 5x — \left| {x — 6} \right| + 9 = 0 \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x — 6 \ge 0, \\ x^2 — 5x — \left( {x — 6} \right) + 9 = 0; \\ \end{array} \right. \\ \left\{ \begin{array}{l} x — 6 < 0, \\ x^2 — 5x + \left( {x — 6} \right) + 9 = 0. \\ \end{array} \right. \\ \end{array} \right.$$	Определение модуля числа $$ \left| a \right| $$	$$\quad $$ $$\left| a \right| = \left[ \begin{array}{l} a,\quad a \ge 0, \\ — a,\quad a < 0. \\ \end{array} \right.$$
$$\quad $$ $$\left| {x — 5} \right| = 3 \Leftrightarrow \left[ \begin{array}{l} x — 5 = 3 \\ x — 5 = — 3 \\ \end{array} \right.$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = a$$	$$\quad $$ $$\left| {f(x)} \right| = a \Leftrightarrow \left\{ \begin{array}{l} a > 0 \\ \left[ \begin{array}{l} f(x) = a,\quad \\ f(x) = — a,\quad \\ \end{array} \right. \\ \end{array} \right.$$
$$\quad $$ $$\left| {x^2 — 4} \right| = 0 \Leftrightarrow x^2 — 4 = 0$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = a$$	$$\quad $$ $$\left| {f(x)} \right| = a \Leftrightarrow \left\{ \begin{array}{l} a = 0 \\ f(x) = 0 \\ \end{array} \right.$$
$$\quad $$ $$\left| {x^2 — 4x} \right| = — 5 \Leftrightarrow x \in \emptyset $$	Свойство равносильности уравнений $$\left| {f(x)} \right| = a$$	$$\quad $$ $$\left| {f(x)} \right| = a \Leftrightarrow \left\{ \begin{array}{l} a < 0, \\ x \in \emptyset . \\ \end{array} \right.$$
$$\quad $$ $$\left| {x^2 — x — 2} \right| = x^2 — x — 2 \Leftrightarrow x^2 — x — 2 \ge 0$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = f(x)$$	$$\quad $$ $$\left| {f(x)} \right| = f(x) \Leftrightarrow f(x) \ge 0$$
$$\quad $$ $$\left| {x^2 — 9} \right| = 9 — x^2 \Leftrightarrow 9 — x^2 \le 0$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = — f(x)$$	$$\quad $$ $$\left| {f(x)} \right| = — f(x) \Leftrightarrow f(x) \le 0$$
$$\quad $$ $$\left| {x + 3} \right| = \left| {2x — 5} \right| \Leftrightarrow \left[ \begin{array}{l} x + 3 = 2x — 5 \\ x + 3 = 5 — 2x \\ \end{array} \right.$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = \left| {g(x)} \right|$$	$$\quad $$ $$\left| {f(x)} \right| = \left| {g(x)} \right| \Leftrightarrow \left[ \begin{array}{l} f(x) = g(x), \\ f(x) = — g(x). \\ \end{array} \right.$$
$$\quad $$ $$\left| {x^2 — 4} \right| = — \left| {x^2 — x — 2} \right| \Leftrightarrow \left[ \begin{array}{l} x^2 — 4 = 0, \\ x^2 — x — 2. \\ \end{array} \right.$$	Свойство равносильности уравнений $$\left| {f(x)} \right| = — \left| {g(x)} \right|$$	$$\quad $$ $$\left| {f(x)} \right| = — \left| {g(x)} \right| \Leftrightarrow \left\{ \begin{array}{l} f(x) = 0, \\ g(x) = 0. \\ \end{array} \right.$$

Пример. Решите уравнение $$x^2 — \left| x \right| — 2 = 0$$

Решение: Введем замену $$\left| x \right| = a,\quad a \ge 0$$, тогда $$x^2 = \left| x \right|^2 = a^2 \Rightarrow a^2 — a — 2 = 0 \Rightarrow a_1 = 2,\;a_2 = — 1$$ — корни уравнения. Вернемся к замене $$\left| x \right| = 2 \Rightarrow x_1 = 2,\;x_2 = — 2$$ и $$\left| x \right| = — 1 \Rightarrow x \in \emptyset $$

Ответ: $$x_1 = 2,\;x_2 = — 2 $$

Для решения используем последовательно знания следующих свойств:

• Метод решения уравнений: введение новой переменной.
• Свойство модуля : $$\left| a \right|^2 = a^2 $$
• Решение квадратного уравнения
• Определение модуля числа $$ \left| a \right| $$ : $$\left| a \right| = \left[ \begin{array}{l} a,\quad a \ge 0, \\ — a,\quad a < 0. \\ \end{array} \right.$$
• Свойство равносильности уравнений $$\left| {f(x)} \right| = a$$ : $$\quad $$ $$\left| {f(x)} \right| = a \Leftrightarrow \left\{ \begin{array}{l} a < 0, \\ x \in \emptyset . \\ \end{array} \right.$$

Проверка гипотез в других областях

Метод проверки гипотез работает не только в математике, алгебре, но и в других науках. Даже в гуманитарных дисциплинах применяют методы проверки гипотез. Скажем, в управлении, в менеджменте.

Допустим, на заводе выпускается продукция, но по какой-то неясной причине некоторые производимые изделия стали бракованными. В чем проблема? Менеджеры начинают строить гипотезы: оборудование износилось и требует ремонта, сырье привезли уже бракованное, рабочий на линии перестал соблюдать установленные требования и так далее.

Может быть даже построено «дерево возможных причин». Оно визуально выглядит, не как дерево с разветвляющимися ветками, а как скелет рыбы, лежащий на боку, где на конце каждой косточки надписана та или иная гипотеза, предположение, почему стали выпускать бракованную продукцию. Подобная схема имеет несколько вполне официальных, признанных наукой названий: «рыбная кость», «рыба Исикавы» (по фамилии ее изобретателя из Японии) и другие.

И затем, «косточка за косточкой», гипотеза за гипотезой, последовательно проверяя их все, менеджеры находят одну или сразу несколько причин возникшей проблемы.

Так что проверка гипотез, логический подход к решению задач, на самом деле, широко распространен в наше время. Изучение этого подхода на простых алгебраических уравнениях, на самом деле, очень полезно, поскольку логика таких решений, возможно, нам всем потребуется в дальнейшей работе и жизни. Причем, совершенно не обязательно, что мы будем решать уравнения, а не заниматься другими делами, скажем, управлением производством или обслуживанием.

«Математика уж тем хороша, что она ум в порядок приводит» — М.В.Ломоносов. Лучше не скажешь, особенно применительно к решению логических задач, так как логика очень часто нужна в повседневной жизни в работе.

Решение уравнений вида \(|f(x)|=g(x)\)

А что, если у нас правая часть переменная (зависит от \(x\)), а не просто число:
$$|4x-2|=x+7;$$
Тогда решение будет немного сложнее, ведь в зависимости от \(x\) правая часть уравнения может быть как отрицательной, так и положительной. Поэтому, прежде чем избавляться от модуля, надо убедиться, что правая часть будет положительной, только в этом случае у нас будут корни:
$$x+7 \geq 0;$$
$$x \geq -7;$$
Если корни уравнения не будут удовлетворять неравенству \(x \geq -7\), то их необходимо будет отбросить.

Само уравнение решается таким же образом, как и уравнения с численной правой частью:
$$
\left[
\begin{gathered}
4x-2=x+7, \\
4x-2=-(x+7).
\end{gathered}
\right.$$

Решим по-отдельности каждое из полученных уравнений:
$$4x-2=x+7;$$
$$4x-x=7+2;$$
$$3x=9;$$
$$x_1=3;$$
И второе уравнение:
$$4x-2=-(x+7);$$
$$4x-2=-x-7;$$
$$4x+x=-7+2;$$
$$5x=-5;$$
$$x_2=-1;$$

Оба полученных корня удовлетворяют неравенству \(x \geq -7\), записываем ответ:Ответ: \(x_1=3\) и \(x_2=-1.\)

Второй способ решения

Снова решим это же уравнение, но воспользовавшись правилами раскрытия модуля:

$$|f(x)|=g(x) \quad \Rightarrow \quad
\left[
\begin{gathered}
f(x)=g(x), \quad если \quad f(x) \geq 0, \\
-f(x)=g(x), \quad если \quad f(x) \lt 0.
\end{gathered}
\right.
$$

В нашем уравнении \(f(x)=4x-2\), а \(g(x)=x+7\):
$$|4x-2|=x+7 \quad \Rightarrow \quad
\left[
\begin{gathered}
4x-2=x+7, \quad если \quad 4x-2 \geq 0, \\
-(4x-2)=x+7, \quad если \quad 4x-2 \lt 0.
\end{gathered}
\right.
$$

Решим по-отдельности каждое уравнение с учетом ограничений:
$$\begin{cases}
4x-2=x+7, \\
4x-2 \geq 0.
\end{cases}$$

$$\begin{cases}
4x-x=2+7, \\
4x \geq 2.
\end{cases}$$

$$\begin{cases}
3x=9, \\
x \geq \frac{1}{2}.
\end{cases}$$

$$\begin{cases}
x_1=3, \\
x \geq \frac{1}{2}.
\end{cases}$$

Так как \(x_1=3 \ge \frac{1}{2}\), то решением первой системы будет \(x_1=3\).
Решим вторую систему:
$$\begin{cases}
-(4x-2)=x+7, \\
4x-2 \lt 0.
\end{cases}$$

$$\begin{cases}
-4x+2=x+7, \\
4x \lt 2.
\end{cases}$$
$$\begin{cases}
-5x=5, \\
x \lt \frac{1}{2}.
\end{cases}$$
$$\begin{cases}
x_2=-1, \\
x \lt \frac{1}{2}.
\end{cases}$$
Ответ: \(x_1=3\) и \(x_2=-1.\)

Внимательный читатель обратил внимание, что в зависимости от того, каким способом решать уравнения с модулем, накладываются разные ограничения. В первом способе мы накладываем ограничение на правую часть уравнения, а во втором способе ограничения накладываются на выражение под модулем

Значит, в уравнениях с модулем вида \(|f(x)|=g(x)\), если проще решить неравенство \(g(x) \geq 0\), то решаем первым способом, а если проще \(f(x) \geq 0\), то вторым.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида . Построим графики функций и и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.

Рассмотрим примеры.

1. Решить уравнение   

Ответ: x = −1.

2. Решить уравнение   

Ответ: x₁ = -2; x₂ = 1.

3. Решить уравнение   

Ответ: x = 2.

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4, а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

1. Предварительный вывод:
2. Проверка:
3. Окончательный вывод

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

\

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $f\left( x \right)$ и $g\left( x \right)$ :

\

Применительно к нашему уравнению получим:

\

Ну, с требованием $2x\ge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

\

Ну и какой их этих двух корней удовлетворяет требованию $2x\ge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5}\;$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

\

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

\

И решается оно точно так же:

\

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

\

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

\

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

\

\

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

\

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

\

\

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3}\;$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

\

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

\

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

\

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

Представьте, что вы стоите в точке на числовой оси. Слева от вас, в точке -100, находится школа. Справа, в точке 50, находится ваш дом. Математически число -100 меньше, чем 50. Но вот идти до школы 100 метров влево гораздо дольше, чем пройти 50 метров до дома вправо. В этом смысле «величина» пройденного расстояния в -100 метров больше, чем 50 метров.

Пусть теперь школа находится в точке -10, а дом в точке 10. Математически вновь получаем, что -10 меньше 10. Но вот нам, находящимся в , совершенно нет разницы: идти -10 метров влево или 10 метров вправо. В обоих случаях мы пройдем 10 метров. То есть, по «величине» числа -10 и 10 равны.

Количественный смысл

Рассмотрим числа 50 и -100. В математическом смысле -100 гораздо меньше 50. А давайте посмотрим на эти числа под другим углом. У вас есть всего 50 рублей и вы задолжали другу. Ваш долг составляет -100 рублей. В этом смысле «величина» вашего долга в -100 рублей гораздо больше имеющихся у вас 50 рублей. Получается, что математически -100 меньше 50, но по «величине» -100 больше 50.

Теперь рассмотрим числа -10 и 10. Математически, опять же, -10 меньше 10. Но, пользуясь нашей аналогией с долгом, своими 10 рублями вы полностью покроете долг в -10 рублей. То есть, по «величине» число -10 равно числу 10.

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.