Нейросеть для решения задач по фото онлайн

Термодинамика

Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:

Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:

Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:

Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:

При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:

При сгорании топлива выделяется количество теплоты равное:

Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):

Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:

Работа идеального газа:

Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:

Изменение внутренней энергии рассчитывается по формуле:

Первый закон (первое начало) термодинамики (ЗСЭ):

Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):

Изобарный процесс (p = const):

Изотермический процесс (T = const):

Адиабатный процесс (Q = 0):

КПД тепловой машины может быть рассчитан по формуле:

Где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:

Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:

Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):

Относительная влажность воздуха может быть рассчитана по следующим формулам:

Потенциальная энергия поверхности жидкости площадью S:

Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:

Высота столба жидкости в капилляре:

При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:

При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

Произведите вычисления

В физике очень важно уметь производить разные вычисления, чтобы находить нужные физические величины. Для этого нужно знать несколько формул и быть уверенным в использовании математических операций

Пример: если нужно найти силу, то можно воспользоваться формулой сила (F) = масса (m) * ускорение (a). Допустим, масса тела равна 10 кг, а ускорение — 5 м/с². Тогда сила будет равна:

Формула	Значение
F = m * a	50 Н

Также часто используется формула скорости: скорость (v) = расстояние (s) / время (t). Например, если расстояние равно 100 м, а время — 10 с, то скорость будет равна:

Формула	Значение
v = s / t	10 м/с

Помимо этих формул, в физике есть множество других, включая формулы для нахождения работы, мощности, плотности и т.д. Их знание и умение применять поможет вам лучше понимать окружающий мир и решать различные задачи.

Задача №1

Представьте, перед вами четыре стакана, наполненных водой. В каждом стакане находятся предметы. Так:

в первом стакане – металлические наручные часы;
во втором стакане – канцелярская скрепка;
в третьем стакане – металлические ножницы;
в четвертом стакане – ластик.

При этом уровень воды во всех стаканах одинаковый. Визуально это выглядит следующим образом:

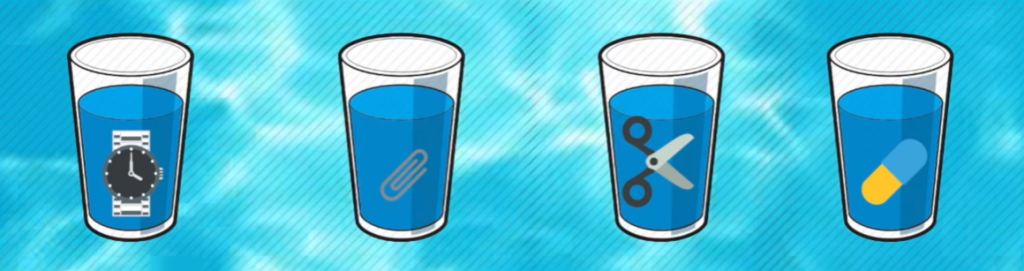
Вопрос: в каком стакане воды больше, чем в остальных?

Ответ

Во втором стакане. Все дело в скрепке, которая по сравнению с другими предметами имеет меньший объём. Соответственно, для необходимого уровня воды требуется больше.

Размялись? Согласитесь, это было несложно. Продолжаем…

Магнетизм

Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:

Момент сил действующих на рамку с током:

Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:

Радиус траектории полета заряженной частицы в магнитном поле:

Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:

Индукция поля в центре витка с током радиусом R:

Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:

Магнитная проницаемость вещества выражается следующим образом:

Магнитным потоком Φ через площадь S контура называют величину заданную формулой:

ЭДС индукции рассчитывается по формуле:

При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):

Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Индуктивность катушки:

Где: n — концентрация витков на единицу длины катушки:

Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:

ЭДС самоиндукции возникающая в катушке:

Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):

Объемная плотность энергии магнитного поля:

Динамика

Второй закон Ньютона:

Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:

Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):

Третий закон Ньютона (сила действия равна силе противодействия):

Сила упругости:

Общий коэффициент жесткости параллельно соединённых пружин:

Общий коэффициент жесткости последовательно соединённых пружин:

Сила трения скольжения (или максимальное значение силы трения покоя):

Закон всемирного тяготения:

Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:

Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:

Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:

Скорость спутника на круговой орбите:

Первая космическая скорость:

Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:

Проверяем каждую идею

Даже опытные программисты далеко не всегда с первого подхода реализуют правильное решение. Обычно создаётся первый, черновой вариант решения, и уже дальше он дорабатывается

В ходе работы над ошибками очень важно проверять каждый участок кода

Постарайтесь проверить каждый промежуточный результат, залогируйте изменения данных, разберите на мелкие детали работу вашего кода. Одна из самых распространенных ошибок в программировании это построение дальнейшего решения на неверных выводах. Например, вы написали какой-то код и считаете, что он работает верно. Далее вы добавляете код, но что-то уже не работает как надо. Можно сделать вывод, что проблема в новом коде, однако вполне возможно, что просто изначальный код был не верен. Такая ситуация опасна тем, что вы можете потратить очень много времени впустую — потому что просто будете искать проблему не в том месте.

Чтобы избежать таких ситуаций, во-первых нужно перепроверять код, особенно когда вы еще только начинаете учиться. Старайтесь избегать утвердительных формулировок по типу «я сделал правильно» или «этот код делает то-то», если вы это точно не проверили. Во-вторых, вы можете показать своё решение другому человеку или с помощью метода утенка описать своими словами, что делает тот или иной участок кода. Есть большая вероятность, что вы сразу обнаружите слабые места в вашем решении, либо собеседник укажет на них.

Общая формула

Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:

S = V * t, где:

S — пройденное объектом расстояние;
V — средняя скорость тела;
t — время, затраченное на преодоление пути.

Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).

Действительно, пусть имеется физическое тело, находящееся в каком-то месте

Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.

В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.

Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

Путь, который преодолевает тело, существенно больше, чем его размеры.
Расстояние между телами значительно превышает их размеры.
Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Нейросеть решает задачи по алгебре

Решение задач — это рутина, которая перевешивает большинство повседневных занятий школьников и студентов. Это также один из тех процессов, который может оставить даже самых способных из нас в тупике. Однако с появлением современных технологий, имеющих отношение к машинному обучению и нейросетям, решение алгебраических уравнений стало гораздо проще, быстрее и точнее.

Решить задачу по алгебре онлайн нейросетью — это максимально удобный способ найти ответ. В отличие от человека, нейросеть может проверить несколько вариантов одновременно и выполнить вычисления быстрее, чем это когда-либо смогут сделать люди. Это означает, что при помощи нейросетей мы можем решить даже самые сложные математические проблемы за несколько секунд.

Работа, мощность, энергия

Механическая работа рассчитывается по следующей формуле:

Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):

Мгновенная механическая мощность:

Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:

Формула для кинетической энергии:

Потенциальная энергия тела поднятого на высоту:

Потенциальная энергия растянутой (или сжатой) пружины:

Полная механическая энергия:

Связь полной механической энергии тела или системы тел и работы внешних сил:

Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):

С чего начать

Обычно самое сложное в решении задачи — сделать первый шаг. Особенно на старте обучения, когда опыта ещё нет, может показаться, что вы совершенно ничего не понимаете и не способны решить даже самое простое упражнение. Если вы читаете задание и у вас нет никаких идей, с чего же вообще начать, мы предлагаем начинать с самых маленьких шагов.

Задания связаны напрямую с теорией, в том числе с пройденной в более ранних курсах. Вы всегда можете вернуться к каким-то урокам, чтобы освежить нужную тему. И так в любых ситуациях — если вы понимаете, что не хватает каких-то знаний, просто вернитесь к предыдущим урокам. Очень сложно запомнить всю информацию, поэтому возврат к уже пройденному материалу — это нормально.

Главный принцип решения задач — дробить задачу на подзадачи. Не пытайтесь сразу решить большое и сложное упражнение с первого подхода, делайте это постепенно. Если в задании сказано написать и экспортировать функцию, напишите пустую функцию и экспортируйте её. Ваш код в большинстве случаев уже будет работать, хоть и не проходить наших тестов. Проверьте примеры вызова функции, которую вам надо написать, посмотрите, что в неё передаётся. И так шаг за шагом продвигайтесь к реализации полного и нужного вам решения.

Процессы в молекулярной физике и их формулы

Замечание 1

Всем понятиям и процессам присущи собственные обозначения, при этом их описывают специальные формулы, которые более наглядно отображают взаимодействия друг с другом определенных параметров. Процессы и явления будут пересекаться в своих проявлениях, различные формулы при этом могут содержать одинаковые по значению величины и выражаться посредством разных способов.

Количество вещества является определяющим для взаимосвязи веса (массы) и количества молекул, которые и будет содержать данная масса. Это обусловлено наличием разного числа минимальных частиц при одинаковой массе для различных веществ. Процессы, осуществляемые на молекулярном уровне, могут пониматься исключительно при рассмотрении количества атомных единиц – непосредственных участников взаимодействий.

Формула для определения количества вещества:

$v = \frac{N}{N_A}$, где:

$m$ — масса,
$N$ — число молекул,
$N_A$ число Авогадро.

Молекулы представляют сложные системы, обладающие многоступенчатым строением. Для упрощения рассмотрим газовые частицы в сосуде в формате упругих однородных шариков, не взаимодействующих при этом друг с другом (это будет идеальный газ). Формула выглядит так:

$P = nkT$, где:

$n$ —концентрация молекул;
$T$ —абсолютная температура.

Определить количество частиц $d$ в данной массе вещества возможно такой формулой:

$v = \frac{N}{Na}$

Отсюда получается, что число молекул будет определять следующая формула:

$N = vNa$

Один моль всегда будет содержать равное количество минимальных частиц. Таким образом, зная массу моля, возможно разделить ее на число молекул (число Авогадро), с получением в итоге массы системной единицы:

$m = \frac{M}{Na}$

Следует учитывать отношение данной формулы исключительно к неорганическим молекулам. Что касается молекул органического типа, то их размеры намного больше, а их величине или весу свойственны совсем иные значения.

Молярная масса представляет массу в килограммах одного моля вещества. В связи с содержанием в одном моле одинакового количества структурных единиц, формулу молярной массы получаем такую:

$M = κM_r$, где:

$k$ — коэффициент пропорциональности;
$M_r$ — атомная масса вещества.

Молярная масса газа рассчитывается по уравнению Менделеева-Клапейрона:

$pV = \frac{mRT}{M}$

Тогда получаем такую формулу:

$M = \frac{mRT}{pV}$

Формулы, которые содержатся в термодинамике и в молекулярной физике, позволяют вычислять количественные значения для всех процессов, выполняемых в отношении твердых веществ и газов. Такие расчеты важны как для теоретических изысканий, так и в практическом применении, поскольку ориентированы на решение разноплановых задач.

Молекулярная физика

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы. Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

Атомная и ядерная физика

Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:

Импульс фотона:

Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):

Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U_з и элементарный заряд е:

Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:

Второй постулат Бора или правило частот (ЗСЭ):

В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:

На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:

Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:

Дефект массы:

Энергия связи ядра выраженная в единицах СИ:

Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):

Формула альфа-распада:

Формула бета-распада:

Закон радиоактивного распада:

Ядерные реакции

Для произвольной ядерной реакции описывающейся формулой вида:

Выполняются следующие условия:

Энергетический выход такой ядерной реакции при этом равен:

Процесс решения задачи в математике

Понимание задачи: Важно четко понять, что требуется решить, и какие данные или ограничения даны.
Разработка плана: Выбор подходящего метода или стратегии для решения задачи.
Решение: Выполнение шагов плана, чтобы найти решение или ответ.
Проверка: Проверка полученного решения на корректность и соответствие условиям задачи.

Задачи в математике играют важную роль в развитии навыков решения проблем, логического мышления и математической грамотности. Решение математических задач также помогает учащимся применять математические концепции на практике и видеть их в контексте реальных ситуаций.

Ищем ошибки в коде

Важная часть работы над задачей — это поиск ошибок, который начинается с логов. Это то, что выводит программа во время своего выполнения. Например, когда вы запускаете проверку вашего решения во вкладке OUTPUT отображается вывод работы тестов — это и есть логи. Вы можете добавлять к этому выводу любой собственный вывод, используя инструменты своего языка программирования (например в JS — ).

Залогируйте входящие данные — это поможет понять, с чем придётся работать внутри функции. Как это сделать, мы рассказываем в наших справочных материалах. Для удобства вывода логов вы можете добавлять свои метки, чтобы видеть, какая именно переменная выводится. Например, так может выглядеть логирование в JS:

Отметка «START» нужна, чтобы увидеть, в какой именно момент вызывается ваша функция. Например, в упражнениях на Хекслете часто идёт проверка через тесты, которые несколько раз запускают нашу функцию с разными данными. Таким образом, в выводе информации можно будет легче разобраться, что и к какому запуску вашей функции относится.

Иногда вместо логирования гораздо удобнее использовать дебаггер. Например, если вы делаете упражнение, в котором есть Web-доступ, можно открыть DevTools браузера и посмотреть в нём исполняемый код. Здесь вы можете поставить на паузу выполнение программы и посмотреть, чему равны все значения переменных или констант в текущий момент.

Изолируем код

При знакомстве с задачей старайтесь сразу определять сложные моменты и максимально их прорабатывать. Например, если в решении нужно использовать цикл, а вы ещё плохо знакомы с ними, можно отдельно от решения попрактиковаться в их использовании. Старайтесь больше экспериментировать и подводить пример максимально близко к тому, что происходит в задаче.

Выделение изолированных участков кода — еще один важнейший механизм в решении задач. Попробуйте выделить в вашем алгоритме промежуточные результаты — так вы сможете написать отдельные модули, каждый из которых будет вычислять нужный результат. При этом логика таких модулей будет максимально простой и понятной. Тут мы подходим пожалуй к самой сложной вещи: построение алгоритма.

Показательная функция

Функцию вида y=ax, где а > 0, a≠1, х – любое число, называют показательной функцией.
Область определения показательной функции: D (y)=R — множество всех действительных чисел.
Область значений показательной функции: E (y)=R₊-множество всех положительных чисел.
Показательная функция y=ax возрастает при a > 1.
Показательная функция y=ax убывает при 0 .

Справедливы все свойства степенной функции:

а=1 Любое число (кроме нуля) в нулевой степени равно единице.
а1=а Любое число в первой степени равно самому себе.
ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
а-х=1/ax
(a/b)-x=(b/a)x.

Арифметическая прогрессия

Определение арифметической прогрессии

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом d, называют арифметической прогрессией. Число d называют разностью арифметической прогрессии. В арифметической прогрессии {a_n}, т. е. в арифметической прогрессии с членами: a₁, a₂, a₃, a₄, a₅, …, a_n-1, a_n, … по определению: a₂=a₁+d; a₃=a₂+d; a₄=a₃+d; a₅=a₄+d; …; a_n=a_n-1+d; …

Свойства арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:

a_n=(a_n-1+a_n+1):2;

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому равноотстоящих от него членов:

a_n=(a_n-k+a_n+k):2.

Решить задачу по биологии онлайн

Решить задачу по биологии с помощью нейросетей — это намного более удобный и эффективный способ, чем поиск решения в интернете. И вот почему:

Во-первых, нейросети позволяют автоматически обрабатывать и анализировать большие объемы данных, что значительно сокращает время, необходимое для решения сложных задач.
Во-вторых, они могут выявить скрытые закономерности и зависимости, что делает процесс исследования более глубоким и точным.
Кроме того, нейросети могут быстро адаптироваться к новым данным и условиям, что позволяет сохранять актуальность результатов даже в быстро меняющейся среде.
В итоге использование нейросетей в биологических задачах является не только более удобным, но и более перспективным подходом, который может значительно ускорить развитие науки.

Электрический ток

Сила тока может быть найдена с помощью формулы:

Плотность тока:

Сопротивление проводника:

Зависимость сопротивления проводника от температуры задаётся следующей формулой:

Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):

Закономерности последовательного соединения:

Закономерности параллельного соединения:

Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:

Закон Ома для полной цепи:

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Сила тока короткого замыкания:

Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:

Мощность электрического тока:

Энергобаланс замкнутой цепи

Полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

Где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея: