I. механика

Невесомость

Выясним некоторые особенности веса. Вес – это сила, с которой тело давит на опору или растягивает подвес, из этого следует, что если тело не подвешено или не закреплено на опоре, то его вес равен нулю. Данный вывод кажется противоречивым нашему повседневному опыту. Однако он имеет вполне справедливые физические примеры.

Если пружину с подвешенным к ней телом отпустить и позволить ей свободно падать, то указатель динамометра будет показывать нулевое значение (Рис. 4). Причина этого проста: груз и динамометр движутся с одинаковым ускорением (g) и одинаковой нулевой начальной скоростью (V0). Нижний конец пружины движется синхронно с грузом, при этом пружина не деформируется и силы упругости в пружине не возникает. Следовательно, не возникает и встречной силы упругости, которая является весом тела, то есть тело не обладает весом, или является невесомым.            

Рис. 4. Свободное падение пружины с подвешенным к ней телом

Состояние невесомости возникает благодаря тому, что в земных условиях сила тяжести сообщает всем телам одинаковое ускорение, так называемое ускорение свободного падения. Для нашего примера мы можем сказать, что груз и динамометр движутся с одинаковым ускорением. Если на тело действует только сила тяжести или только сила всемирного тяготения, то это тело находится в состоянии невесомости

Важно понимать, что в этом случае исчезает только вес тела, но не сила тяжести, действующая на это тело

Состояние невесомости – не экзотика, довольно часто многие из вас его испытывали – любой человек, подпрыгивающий или спрыгивающий с какой либо высоты, до момента приземления находится в состоянии невесомости.

Рассмотрим случай, когда динамометр и прикрепленное к его пружине тело движутся вниз с некоторым ускорением, но не совершают при этом свободного падения. Показания динамометра уменьшатся по сравнению с показаниями при неподвижном грузе и пружине, значит, вес тела стал меньше, чем он был в состоянии покоя. В чем причина такого уменьшения? Дадим математическое объяснение, опираясь на второй закон Ньютона.

Рис. 5. Математическое объяснение веса тела

На тело действуют две силы: сила тяжести, направленная вниз, и сила упругости пружины, направленная вверх. Эти две силы сообщают телу ускорение. и уравнение движения будет иметь вид:

 m =  + m

Выберем ось y (Рис. 5), поскольку все силы направлены вертикально, нам достаточно одной оси. В результате проецирования и переноса слагаемых получим – модуль силы упругости будет равен:

ma =  mg — Fупр

Fупр =  mg — ma,

где в левой и правой части уравнения стоят проекции сил, указанных во втором законе Ньютона, на ось y. Согласно определению, вес тела по модулю равен силе упругости пружины, и, подставив ее значение, получим :

P = Fупр =  mg — ma = m( g — а)

Вес тела равен произведению массы тела на разность ускорений. Из полученной формулы видно, что если модуль ускорения тела меньше модуля ускорения свободного падения, то вес тела меньше силы тяжести, то есть вес тела, движущегося ускоренно, меньше веса покоящегося тела.

Рассмотрим случай, когда тело с грузиком движется ускоренно вверх (Рис. 6).

Стрелка динамометра покажет значение веса тела большее, чем покоящегося груза.

Рис. 6. Тело с грузиком движется ускоренно вверх

Тело движется вверх, и его ускорение направлено туда же, следовательно, нам необходимо поменять знак проекции ускорения на ось у.

Из формулы видно, что теперь вес тела больше силы тяжести, то есть больше веса покоящегося тела.

Увеличение веса тела, вызванное его ускоренным движением, называется перегрузкой.

Это справедливо не только для тела, подвешенного на пружине, но и для тела, укрепленного на опоре.

Рассмотрим пример, в котором проявляется изменение тела при его ускоренном движении (Рис. 7).

Автомобиль движется по мосту выпуклой траектории, то есть по криволинейной траектории. Будем считать форму моста дугой окружности. Из кинематики мы знаем, что автомобиль движется с центростремительным ускорением, величина которого равна квадрату скорости, деленной на радиус кривизны моста. В момент нахождения его в наивысшей точке, это ускорение будет направлено вертикально вниз. Согласно второму закону Ньютона это ускорение сообщается автомобилю равнодействующей силой тяжести и силой реакции опоры.

m =  + m

Выберем координатную ось у, направленную вертикально вверх, и запишем это уравнение в проекции на выбранную ось, подставим значения и проведем преобразования:

Рис. 7. Наивысшая точка нахождения автомобиля

Вес автомобиля, по третьему закону Ньютона, равен по модулю силе реакции опоры (), при этом мы видим, что вес автомобиля по модулю меньше силы тяжести, то есть меньше веса неподвижного автомобиля.

История понятия

Понятие силы использовали ещё ученыеантичностив своих работах остатикеи движении. Изучением сил в процессе конструированияпростых механизмовзанимался в III в. до н. э.Архимед. ПредставленияАристотеляо силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в.Исаак Ньютон, используя для описания силы математические методы.МеханикаНьютона оставалась общепринятой на протяжении почти трехсот лет. К началу XX в.Альберт Эйнштейнвтеории относительностипоказал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положениякинематикиидинамикии описав некоторые новые свойствапространства-времени.

Определение силы

В инерциальной системе отсчета, не взаимодействующие между собой, материальные точки движутся с постоянными скоростями. Пусть – радиус-вектор одной из свободных точек. Тогда вектор ее скорости есть постоянный вектор, не зависящий от времени . Следовательно его проекции на оси прямоугольной системы координат являются постоянными, не зависящими от времени величинами: . Если мы определим вектор ускорения точки:, то он равен нулю: . Это означает, что его проекции на оси координат равны нулю: .

Как показывает опыт, можно создать условия, при которых материальные точки будут взаимодействовать друг с другом. Тогда их скорости не будут постоянными – движение при взаимодействии является ускоренным. У рассматриваемой нами точки, вектор скорости будет зависеть от времени, а вектор ускорения будет отличен от нуля. Тогда удобно ввести новую векторную физическую величину, пропорциональную вектору ускорения точки. Такую величину называют силой. Она определяется по формуле:, где – еще одна физическая величина, называемая массой точки.

Сила ,

действующая на материальную точку с радиус-вектором со стороны других точек – это мера воздействия других точек на рассматриваемую точку, в результате которой она получает ускорение относительно инерциальной системы отсчета. Величина силы определяется по формуле:(1)   , где – масса точки – величина, зависящая от свойств самой точки.

Формула называется вторым законом Ньютона. По существу, она является определением новой физической величины – силы. Такое определение согласуется с нашим жизненным опытом, согласно которому, чем больше мы прилагаем усилий, тем быстрее разгоняется груз (например, при толкании ядра в легкой атлетике). Однако, в отличие от жизненного опыта, формула дает строгое математическое определение.

Изучая движения материальных точек, мы можем экспериментально определить их ускорения, а затем по формуле найти зависимость силы от положений точек системы. Так мы устанавливаем законы, описывающие взаимодействие материальных точек. Изучая и систематизируя экспериментальные данные, мы получаем правила, которые позволяют нам определять зависимость силы от времени и от координат в сложных случаях, основываясь на более простых. Так если нам известна зависимость вектора от времени и от координат: , то формула представляет собой систему дифференциальных уравнений: Решая ее, можно найти закон движения точки.

Деформация

Упругая и неупругая деформация. Сила упругости. Закон Гука.

Ранее были рассмотрены гравитационные силы, теперь же перейдем к изучению сил другой природы – упругих. Они возникают при деформациях тел. А что же такое деформация?

Под деформацией в физике понимают изменение формы тела или его объема. Деформации тела возникают при воздействии на него каких-то внешних сил. Например, растягивая пружинку, можно изменить ее форму, а ложась на надувной матрас (в надутом состоянии) – его объем.

При любой деформации внутри тела возникают силы, которые сопротивляются внешнему воздействию – упругие силы. В названных примерах – пружинка пытается сжаться обратно, а воздух в матрасе сжимается, но не позволяет матрасу совсем просесть под тяжестью тела.

Выделяют упругие и неупругие деформации.

Упругая деформация — такая деформация, при которой тело восстанавливает свою изначальную форму (или объем), когда сила, вызвавшая деформацию, перестает действовать.

Соответственно, неупругая деформация – необратимый вид деформации, при которой тело уже не может вернуться в свой первоначальный вид. Например, когда пружинку растянули слишком сильно и она уже не может вернуть виткам первоначальный вид или же когда пружинка вовсе порвалась от воздействия. Примером неупругой деформации может так же служить пластилин, который после смятия не возвращает исходную форму.

Рассмотрим малые упругие деформации тел. Для такого рода деформация английским ученым Р. Гуком был выведен закон, позже названный именем ученого: модуль силы упругости прямо пропорционален модулю изменения длины тела.

Закон Гука можно записать в виде формулы:

где F_упр – модуль силы упругости, k – коэффициент жесткости,  – модуль изменения длины (см. рисунок 3).

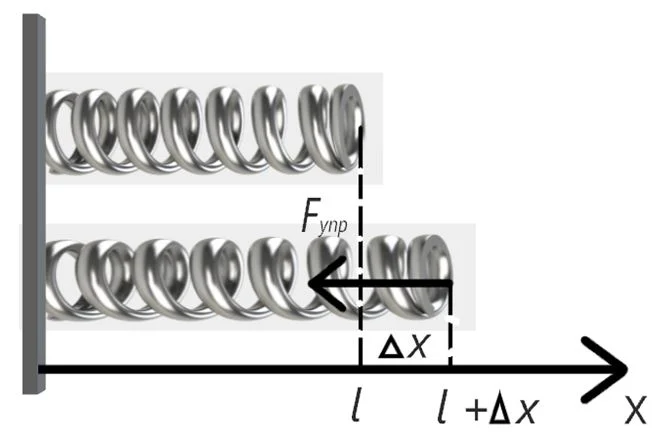Рисунок 3 – Иллюстрация к закону Гука

Коэффициент жесткости (k) – характеристика непосредственно деформированного тела. Зависит от его состава, размеров, температуры и прочего. Как правило, определяется экспериментально. Измеряется коэффициент жесткости в Ньютонах на метр:

Направление силы упругости всегда противоположно деформации. Если вернуться к пружинке – при сжатии силы упругости пытаются ее разжать, при растяжении – силы упругости пытаются ее сжать обратно.

Рассмотрим две задачи, которые часто встречаются на экзаменах: две пружинки соединены в систему параллельно и последовательно.

Параллельное соединение (см. рисунок 4)

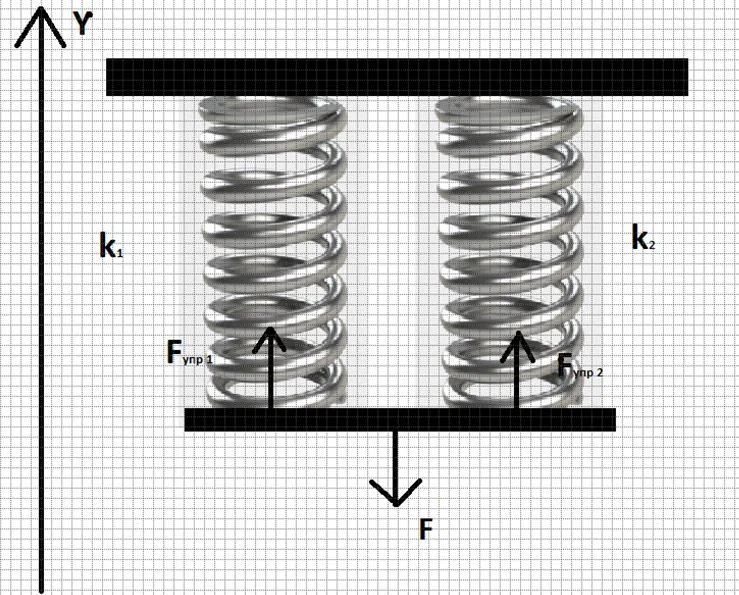Рисунок 4 – Параллельное соединение пружинок

Из рисунка очевидно, что при параллельном соединении удлинение у пружинок при воздействии на них силой F будет одинаковым. Обозначим это удлинение △x. Силы упругости, возникающие в первой и во второй пружинках соответственно обозначим F_упр1 и F_упр2. По закону Гука модули сил упругости будут равны:

Из этой формулы видно, что если бы вместо соединения двух пружинок была взята одна пружинка с жесткостью (k₁+k₂), характеристики системы не поменялись бы. Поэтому при параллельном соединении пружинок суммарная жесткость считается как сумма жесткостей:

k = k₁ + k₂.

Последовательное соединение (см. рисунок 5)

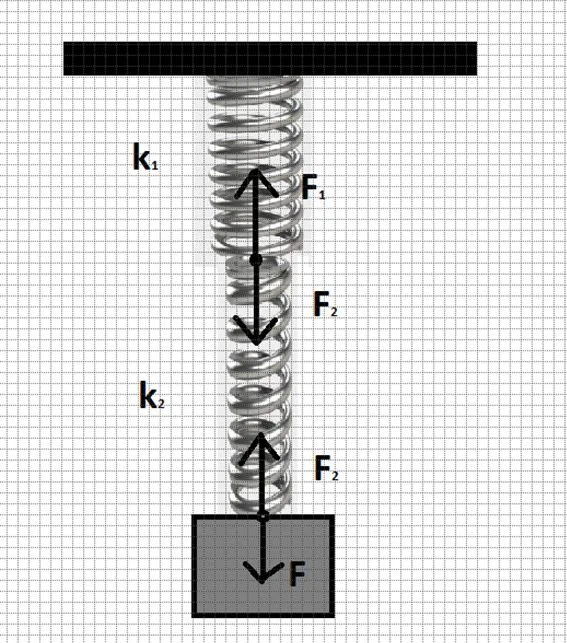Рисунок 5 – Последовательное соединение пружин

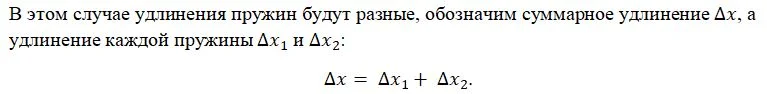
А вот силы F₁ и F₂ будут равны по модулю, так как если между верхней и нижней пружинкой поместить какой-то предмет, верхняя пружинка будет действовать на него с силой F₁, нижняя – с силой F₂. Так как система находится в покое, по второму закону Ньютона эти силы будут равны.*

*Тут можно было бы еще сослаться на третий закон Ньютона: как первая пружина действует на вторую, так и вторая действует на первую. Более понятное объяснение пусть читатель выберет для себя сам.

Еще стоит упомянуть, почему на рисунке два раза изображена сила F₂: из практики должно быть известно, что пружина пытается сжаться с двух сторон (то есть два ее конца стремятся к центру).

Выразим из закона Гука удлинение:

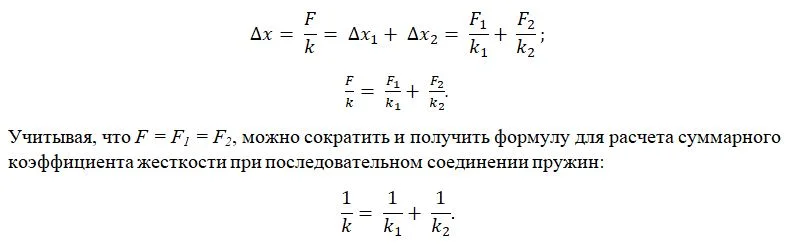
Первая космическая скорость

три раза (6 в 3 раза больше 2). Это также увеличивает расстояние между сферами в три раза. В этом случае сила притяжения между ними уменьшается в 3,2 раза или в 9 раз. Поскольку в первом случае сила была 1 нН, во втором случае она будет в 9 раз меньше, т.е. 1 нН.

Вывод формулы первой космической скорости

Какова сила притяжения между двумя другими звездами, если расстояние между их центрами такое же, как в первом случае, а массы звезд равны 3 и 4 м?

1. Записать исходные данные.
2. Записать закон всемирного тяготения.
3. Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
4. На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.

В 1798 году британский физик Генри Кавендиш провел один из первых в мире высокоточных экспериментов по определению точного значения гравитационной постоянной G. Он сконструировал так называемый торсионный прибор. Он сконструировал так называемые торсионные весы, прикрепив два маленьких свинцовых шарика к концам балки, подвешенной горизонтально на тонкой проволоке. Рядом с каждым из шаров физик поместил большую сферическую свинцовую гирю. Маленькие свинцовые шарики под действием силы тяжести притягивались к тяжелым свинцовым грузам, заставляя проволоку слегка скручиваться. Это явление позволило ему рассчитать величину G.

Примечательно, что оценка G Кавендишем отличалась всего на 1% от принятого сейчас значения 6,674 × 10^-11 м^3/кг^1 * с^2. Чтобы получить точное значение, ученым необходимо разработать невероятно чувствительное оборудование.

• Расстояние между двумя шарами в первом случае: R₁= 2 м.
• Расстояние между двумя шарами во втором случае: R₂= 6 м.
• Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.

Немецко-американский физик Альберт Эйнштейн произвел очередную революцию в понимании гравитации. Общая теория относительности показала, что гравитация возникает в результате искривления пространства-времени, а это означает, что даже а-лучи света, которые должны следовать этому искривлению, преломляются чрезвычайно массивными объектами. В рамках его теории гравитация рассматривается не как сила, действующая на тела, а как искривление пространства и времени под действием массы и энергии.

Теории Эйнштейна были использованы для объяснения существования черных дыр — небесных объектов, настолько массивных, что даже свет не может покинуть их поверхность. Вблизи черной дыры закон Ньютона о всеобщем тяготении уже не может точно описать движение объектов.₁Решение₂.

R₂В своей специальной теории относительности Эйнштейн заявил, что законы физики одинаковы для всех наблюдателей, которые не движутся с ускорением, и показал, что скорость света в вакууме одинакова независимо от скорости, с которой движется наблюдатель. Таким образом, он обнаружил, что пространство и время связаны между собой и что события, происходящие в одно и то же время для одного наблюдателя, могут происходить в разное время для другого наблюдателя.₁Разрабатывая уравнения общей теории относительности, Эйнштейн понял, что массивные объекты вызывают искажение пространства-времени. Представьте, что в центр батута помещен большой предмет. Предмет давит на ткань, образуя выбоины. Если вы затем попытаетесь прокатить мяч по краю батута, он по спирали вонзится внутрь объекта.

Вращение такого тяжелого объекта, как Земля, должно искривлять и искажать пространство-время вокруг нее. НАСА запустило гравитационный зонд B в 2004 году, и, по данным агентства, оси точно откалиброванных гироскопов спутника с течением времени дрейфовали очень незначительно, в соответствии с теорией Эйнштейна.

Силы трения

Виды трения

Любое движение тел, кроме движения в безвоздушном пространстве, сопровождается трением, обуславливающим: замедление движения автомобиля по горизонтальной дороге при выключении двигателя, движение бревен по течению реки при сплаве, сопротивление воздуха свободному падению тел и т.д.

Различают три вида трения: покоя, скольжения и качения.

Сила трения покоя – это сила, которая проявляется между соприкасающимися поверхностями тел, неподвижных относительно друг друга.

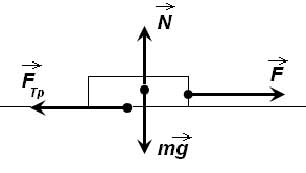
Ш. Кулон экспериментально установил, что максимальное значение модуля силы трения покоя прямо пропорционально модулю силы реакции опоры:

— коэффициент пропорциональности, называемый коэффициентом трения покоя. Характеризует обе трущиеся поверхности и зависит только от вида материала тел и качества обработки их поверхности.

Сила трения скольжения—это сила, возникающая между соприкасающимися поверхностями тел, движущихся относительно друг друга.

Сила трения скольжения всегда направлена против движения тела.

— коэффициент трения скольжения

Сила трения качения. Тела могут не только двигаться поступательно, но и вращаться вокруг той или иной оси. Вращательное действие любой силы определяется её моментом, зависящим от расстояния между осью вращения до той прямой, вдоль которой действует сила.

Данный закон был экспериментально установлен Ш. Кулоном в 1781 г.

Коэффициент трения качения

Поэтому для уменьшения сил трения в технике применяют колеса, шариковые и роликовые подшипники.

Причины возникновения трения

Природа силы трения — электромагнитная. Это означает, что причиной её возникновения являются силы взаимодействия между частицами, из которых состоит вещество. Второй причиной возникновения силы трения является шероховатость поверхности. Выступающие части поверхностей задевают друг за друга и препятствуют движению тела. Именно поэтому для движения по гладким (полированным) поверхностям требуется прикладывать меньшую силу, чем для движения по шероховатым.

Жидкое трение

Явление трения наблюдается и при движении тела в газах и жидкостях. Опыты показывают, что сопротивление движению тел в газах и жидкостях зависит от площади поперечного сечения тела, от его формы и скорости движения. Поэтому телам, движущимися в газах и жидкостях придают обтекаемую форму.

Сила сопротивления, оказываемая средой движущемуся телу, зависит от обработки поверхности тела.

Сила сопротивления зависит и от свойств среды (например, сопротивление движению в воде во много раз больше, чем в воздухе).

При небольших скоростях сила сопротивления пропорциональна скорости тела.

При больших скоростях сила сопротивления пропорциональна квадрату скорости тела.

Значение явления трения в природе и технике

Очень красочно о роли трения пишет французский физик Гильом:
“Всем нам случалось выходить в гололедицу: сколько усилий требовалось, чтобы удерживаться от падения, сколько смешных движений приходилось нам проделывать, чтобы устоять! Это заставляет нас признать, что земля, по которой мы ходим, обладает драгоценным свойством, благодаря которому мы сохраняем равновесие без особых усилий. Та же мысль возникает у нас, когда мы едем на велосипеде по скользкой мостовой или когда лошадь скользит по асфальту и падает. Изучая подобные явления, мы приходим к открытию тех следствий, к которым приводит трение. Инженеры стремятся устранить его в машинах – и хорошо делают. В прикладной механике о трении говорится, как о крайне нежелательном явлении, и это правильно, однако лишь в узкой специальной области. Во всех прочих случаях мы должны быть благодарны трению: оно дает нам возможность ходить, сидеть и работать без опасения, что книги и чернильница упадут на пол. Трение представляет настолько распространенное явление, что нам, за редким исключением, не приходится призывать его на помощь: оно является к нам само.

Трение способствует устойчивости. Плотники выравнивают пол так, что столы и стулья остаются там, куда их поставили. Блюда, стаканы, поставленные на стол, остаются неподвижными без особых забот с нашей стороны, если только дело не происходит на пароходе во время качки.

Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиной с каменную глыбу или малы, как песчинки, никогда не удержится одно на другом. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкой капли”.

Скользящие векторы

Теперь рассмотрим абсолютно твердое тело. Законы его движения имеют более сложный вид. Они описываются двумя векторными уравнениями:(2)   ;(3)   . Здесь – ускорение центра масс тела; – его масса; – момент импульса тела относительно произвольно выбранного центра ; – внешние силы, действующие на тело, приложенные в точках .

Вместо того, чтобы пытаться в лоб решать эти уравнения, давайте попробуем вывести некоторые закономерности, заключенные в этих уравнениях. Для этого упростим задачу. Рассмотрим тело в некоторый момент времени . И пусть, для этого момента времени, нам известны действующие на него силы и точки их приложения .

Уравнение не зависит от точек приложения сил. Для его составления требуется знать только проекции сил на оси координат . А вот в уравнение входят точки приложения. Они входят в виде векторов, проведенных из некоторого центра в точку . Причем входят в виде векторного произведения .

Согласно одному из свойств, векторное произведение векторов, имеющих одинаковое направление, равно нулю. Поэтому . Тогда если к вектору прибавить любой вектор, параллельный , то векторное произведение не изменится:. Здесь – произвольная постоянная, имеющая размерность м/Н.

Отсюда следует важный вывод. Если точку приложения силы переместить на любое расстояние вдоль линии действия силы, то уравнения движения твердого тела не изменятся. В связи с этим, вместо обычного в математическом определении вектора, можно ввести новый математический объект, называемый скользящим вектором. Скользящий вектор по существу есть множество, состоящее из двух векторов – самого вектора силы (так называемый образующий вектор) и его точки приложения относительно выбранного центра системы отсчета . В связи с этим, приводим следующие определения.

Скользящий вектор

– это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, проведенной через точку приложения параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.

Наряду со скользящим вектором, мы можем ввести понятия закрепленных и свободных векторов.

Закрепленный вектор

– это множество, состоящее из образующего вектора и точки его приложения. Два фиксированных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.

Свободный вектор

– это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.

Таким образом, свободный вектор не зависит от точки приложения, и является просто вектором. Для справок также приведем определение вектора.

Вектор в трехмерном пространстве

– это три числа, называемые компонентами, связанные с предварительно выбранной прямоугольной системой координат, которые при поворотах этой системы вокруг ее центра , и при отражении осей, преобразуются по тому же закону, что и координаты произвольной точки , не совпадающей с . Компоненты вектора также называются проекциями вектора на оси координат.