Основы геометрии

Введение

Мы на­чи­на­ем изу­че­ние гео­мет­рии. Это древ­няя наука, воз­ник­ла еще за 300 лет до нашей эры. В пе­ре­во­де с гре­че­ско­го «гео­мет­рия» – «зем­ле­ме­рие», изу­ча­ет она гео­мет­ри­че­ские фи­гу­ры и их свой­ства.

Под­раз­де­ля­ет­ся на два боль­ших раз­де­ла:

— пла­ни­мет­рия – гео­мет­рия на плос­ко­сти,

— сте­рео­мет­рия – гео­мет­рия в про­стран­стве.

При­ме­ры плос­ких фигур – тре­уголь­ник, окруж­ность и т.д. Мы с ними зна­ко­мы.

Мы зна­ко­мы и с про­стран­ствен­ны­ми фи­гу­ра­ми – шар, куб, па­рал­ле­ле­пи­пед и т.д., т.е. гео­мет­рия – во­круг нас.

Мы ска­за­ли, что гео­мет­рия изу­ча­ет свой­ства гео­мет­ри­че­ских фигур.

А что такое гео­мет­ри­че­ская фи­гу­ра? Это любое мно­же­ство, любая со­во­куп­ность точек.

Точки обо­зна­ча­ют боль­ши­ми ла­тин­ски­ми бук­ва­ми.

По­ня­тие о пря­мой дает тон­кая нить, про­дол­жен­ная бес­ко­неч­но в обе сто­ро­ны.

Точка и пря­мая – это неопре­де­ли­мое из­на­чаль­ное по­ня­тие, это ма­те­ма­ти­че­ская иде­а­ли­за­ция – раз­ме­ров они не имеют.

Если точки обо­зна­ча­ют­ся боль­ши­ми бук­ва­ми, то пря­мая может обо­зна­чать­ся ма­лень­ки­ми ла­тин­ски­ми бук­ва­ми.

Об­ри­су­ем в общих чер­тах, как стро­ит­ся гео­мет­рия. Мы упо­мя­ну­ли два по­ня­тия: точка, пря­мая . Это из­на­чаль­ные неопре­де­ли­мые по­ня­тия, их свой­ства вы­ра­жа­ют­ся в ак­си­о­мах, т.е. в ис­ти­нах, ко­то­рые не тре­бу­ют до­ка­за­тельств.

Опре­де­ле­ние дру­гих фигур, на­при­мер, окруж­но­сти, шара и т.д., до­ка­зы­ва­ют­ся тео­ре­ма­ми, таким об­ра­зом, изу­ча­ют­ся свой­ства гео­мет­ри­че­ских фигур. Итак, все гран­ди­оз­ное зда­ние гео­мет­рии ба­зи­ру­ет­ся, во-пер­вых, на неопре­де­лен­ных по­ня­ти­ях, во-вто­рых, на ак­си­о­мах.

Да­вай­те сфор­му­ли­ру­ем три важ­ней­шие ак­си­о­мы, ко­то­рые ха­рак­те­ри­зу­ют вза­им­ное рас­по­ло­же­ние точек и пря­мых и рас­смот­рим их.

Измерение углов

Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:

Градусная мера

Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \ оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.

Мы измеряем время в часах, минутах и ​​секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов

• 1 градус = 60 минут, обозначаемый как 1° = 60′.
• 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.

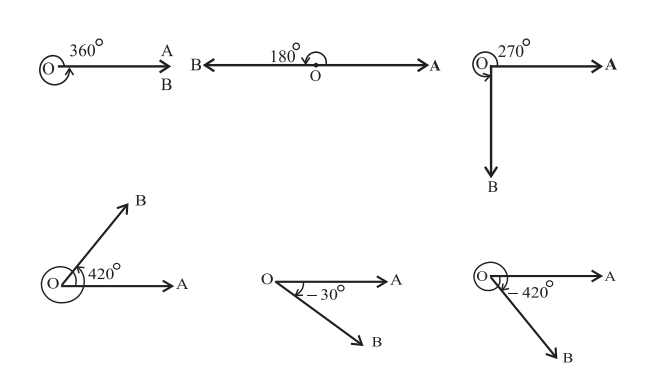Несколько примеров углов с их измерениями

Радианная мера

Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:

Вот еще несколько примеров углов: -1 радиан, радиан, \ радиан, \ радиан.

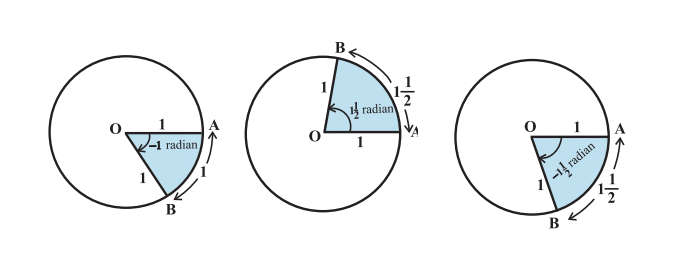
Длина окружности = \ где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \. Следовательно, один полный оборот начальной стороны образует в центре угол \ радиан. Обобщая это, имеем:

В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \ радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:

\

\

Связь между степенью и радианными мерами

По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:

• 360° – по градусной мере
• \ радиан — в радианах

Следовательно, \ радиан = 360° ⇒ \ радиан = 180°. Теперь подставим приблизительное значение \ как \ в уравнении выше и получить, 1 радиан \. Кроме того, \ радиан = 0,01746 радиан примерно. Ниже таблица, изображающая соотношение между градусами и радианами некоторых распространенных углов:

Градусы	\	\	\	\	\	\	\
Радианы	\	\	\	\	\	\	\

Пример

Преобразуйте 40° 20′ в радианы.

Решение: мы знаем, что 1° = 60′, следовательно, 20′ = \.

Следовательно,

\;

Кроме того, мы знаем, что

радианная мера = \ градусную меру

Следовательно, радианная мера \ радиан.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Совпадающие прямые

Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).

Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.

Проведем одну прямую через точки A и D, а вторую прямую — через точки В и С.

Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.

Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.

Знакомство с геометрией

Геометрия – это раздел математики, который изучает фигуры, их свойства и отношения между ними. Благодаря геометрии мы можем абстрагироваться от базовых свойств предметов и зрительно воссоздавать их образы для анализа и изучения. Геометрические фигуры могут быть самыми различными и найти их мы можем везде, начиная от простых повторяющихся узоров на ткани и заканчивая элементами большого строительства.

Знание геометрии может быть полезно в многих областях, например, в научных исследованиях, проектировании и конструировании. Но, еще более важным для геометрии является ее применение в жизни людей: использование геометрических принципов архитекторами и строителями позволяет создавать красивые и устойчивые здания, а использование ее элементов в дизайне помогает создать комфортное пространство для жизни и работы.

• Ключевые понятия геометрии:
  • Фигуры — геометрические объекты, изучаемые в геометрии
  • Угол — часть плоскости между двумя лучами с общей начальной точкой
  • Строение фигур — количество и формирование отрезков прямых линий вокруг геометрических фигур
  • Диаметр — прямая, проходящая через центр круга и соединяющая две противоположные точки на его окружности
  • Радиус — отрезок, соединяющий центр круга с любой точкой на его окружности

Геометрия также предоставляет нам возможности для развивающих задач и игр, помогающих нам учится и развиваться. Проникнись интересом к геометрии и попытайся применить свои знания на практике.

Отрезок — что это за фигура

Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.

Отрезок — это составная часть прямой, расположенная между двумя точками.

Вы можете дать определение также исходя из структурного подхода:

Отрезок — это такая математическая фигура, которая состоит из следующих элементов:

• начало отрезка;
• конец фигуры;
• прямая линия.

С этими составными частями вы можете ознакомиться на слайде:

В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.

Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.

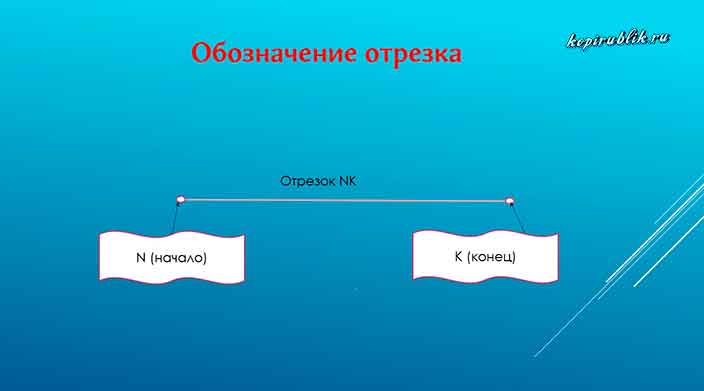
Важная характеристика, которая присуща любому отрезку – его длина.

Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.

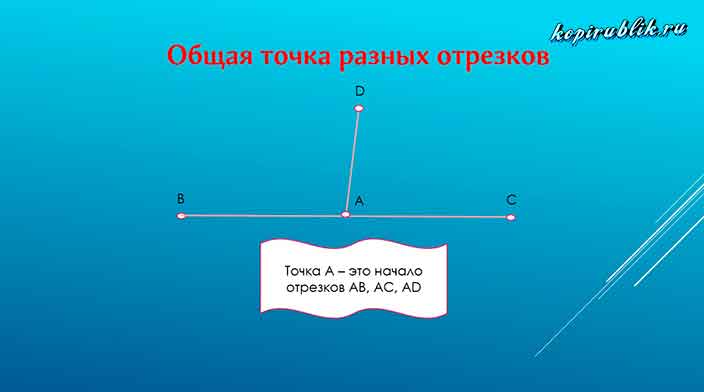
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.

Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.

Геометрические понятия

В жизни мы часто встречаемся с такими выражениями  как “точка на карте”, “идти по прямой” или “угол комнаты”. Но знали ли вы, что в этих фразах упоминаются термины из геометрии?

Для начала давайте разберемся именно с геометрическими терминами.

Что такое точка, прямая, луч, отрезок и угол?

Точка – это математический объект, точного определения для которого не существует.

Прямая – это бесконечная линия.

Луч – это прямая, ограниченная точкой с одной стороны. У луча есть начало, но нет конца.

Что общего у солнечного луча и геометрического?Солнечный луч и геометрический луч отличаются друг от друга почти во всем. Но и тот, и другой имеет начало и не имеет конца.

Отрезок – это прямая, ограниченная точками с обеих сторон. Отрезок состоит из бесконечного множества точек, лежащих на линии между концами отрезка.

Чем отличается луч от отрезка?

Луч ограничен только с одной стороны, а отрезок ограничен с двух.

Угол – это фигура, образованная двумя лучами, исходящими из одной точки.

Можно ли кого-то наказать углом?Провинившегося ребенка могут поставить в угол. Возможно ли поставить кого-то в геометрический угол? Да. Для такого наказания можно использовать не только прямой угол, но и тупой, и даже некоторые острые углы. Только, пожалуй,  не очень узкие острые углы, иначе человек туда просто не поместится.

Аксиома 5

Ак­си­о­ма 5 го­во­рит о дру­гих точ­ках, ко­то­рые лежат по одну сто­ро­ну от дан­ной точки. Она будет рас­смот­ре­на позже.

На дан­ный мо­мент мы имеем три неопре­де­ли­мых по­ня­тия: точка, пря­мая, «ле­жать между». Имеем пять ак­си­ом, ко­то­рые ха­рак­те­ри­зу­ют вза­и­мо­от­но­ше­ния между этими по­ня­ти­я­ми. Пора нам дать опре­де­ле­ние важ­ной гео­мет­ри­че­ской фи­гу­ре – от­рез­ку.

Что же такое от­ре­зок?

От­рез­ком  на­зы­ва­ет­ся гео­мет­ри­че­ская фи­гу­ра, со­сто­я­щая из точек , , и всех точек пря­мой, рас­по­ло­жен­ных между точ­ка­ми  и .

Более крат­кое: от­ре­зок – это часть пря­мой, огра­ни­чен­ная точ­ка­ми  и  (см. рис. 6).

Рис. 6. От­ре­зок

Точки  и  на­зы­ва­ют­ся кон­ца­ми от­рез­ка. От­ре­зок обо­зна­ча­ет­ся так же, как и пря­мая. Пря­мая может обо­зна­чать­ся двумя точ­ка­ми, ле­жа­щи­ми на ней, – , и от­ре­зок может обо­зна­чать­ся таким же об­ра­зом – . Из кон­тек­ста ясно, когда речь идет о пря­мой и когда речь идет об от­рез­ке. Дан­ный от­ре­зок лежит на пря­мой, у пря­мой и от­рез­ка бес­чис­лен­ное мно­же­ство общих точек.

Могут быть дру­гие слу­чаи. Есть пря­мая , от­ре­зок  – это часть дру­гой пря­мой. От­ре­зок  и пря­мая  не имеют общих точек. Го­во­рят, что точки  и  лежат по одну сто­ро­ну от пря­мой  (см. рис. 7).

Рис. 7. Точки  и  лежат по одну сто­ро­ну от пря­мой 

От­ре­зок , пря­мая . Точки  и  лежат по раз­ные сто­ро­ны от пря­мой , зна­чит, от­ре­зок  имеет одну общую точку  с пря­мой. Точка  лежит между точ­ка­ми  и  (см. рис. 8). Этот факт по­ня­тен нам из ин­ту­и­тив­ных со­об­ра­же­ний, но тем не менее он ре­гла­мен­ти­ру­ет­ся ак­си­о­мой 6. Она будет по­дроб­но рас­смот­ре­на в конце урока.

Рис. 8. Точки  и  лежат по раз­ные сто­ро­ны от пря­мой 

От­ре­зок  лежит на пря­мой . Пря­мая  и пря­мая  имеют одну общую точку . А могут ли пря­мые иметь еще общие точки, ведь пря­мые про­сти­ра­ют­ся неогра­ни­чен­но? Может, где-то на Луне они еще пе­ре­се­кут­ся и будет еще одна общая точка?

Нам пора до­ка­зать важ­ную первую тео­ре­му, первую в этом курсе.

Основные понятия геометрии

Геометрия — наука, изучающая пространственные фигуры и их свойства.

Точка — это основной элемент геометрии, который не имеет никаких размеров, только положение в пространстве.

Прямая — это бесконечное множество точек, расположенных на одной линии.

Отрезок — это часть прямой между двумя точками, включая эти точки.

Угол — область, образованная двумя лучами, начинающимися в одной точке, называемой вершиной.

Треугольник — фигура, состоящая из трех отрезков, соединяющих три точки.

Четырехугольник — фигура, состоящая из четырех отрезков, соединяющих четыре точки.

Многоугольник — фигура, состоящая из нескольких отрезков, соединяющих точки.

Круг — фигура, состоящая из всех точек плоскости, равноудаленных от одной точки, называемой центром круга.

Радиус — отрезок, соединяющий центр круга с любой точкой на его окружности.

Таблица ниже представляет понятия и определения, связанные с геометрией:

Понятие	Определение
Точка	Основной элемент геометрии, без размеров
Прямая	Бесконечное множество точек, расположенных на одной линии
Отрезок	Часть прямой между двумя точками, включая эти точки
Угол	Область, образованная двумя лучами, начинающимися в одной точке
Треугольник	Фигура, состоящая из трех отрезков, соединяющих три точки
Четырехугольник	Фигура, состоящая из четырех отрезков, соединяющих четыре точки
Многоугольник	Фигура, состоящая из нескольких отрезков, соединяющих точки
Круг	Фигура, состоящая из точек, равноудаленных от одной точки (центра круга)
Радиус	Отрезок, соединяющий центр круга с любой точкой на его окружности

Это лишь небольшая часть основных понятий геометрии. Они позволяют строить сложные фигуры и решать разнообразные геометрические задачи.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2 Периметр: P=(a+b)*2Площадь по стороне и высоте: S = a*h S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α S (Площадь) по двум диагоналям и углу между ними S=(d₁*d₂)/2*sin γ

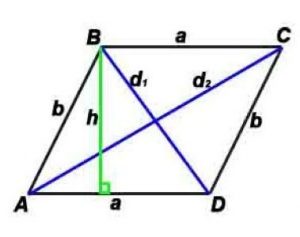где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь, h-высота, проведенная к противоположной сторонеα — угол между сторонами параллелограмма,γ — угол между диагоналями параллелограмма (острый).

Что такое точка?

Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.

Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.

 И строить её умеет даже маленький ребенок.

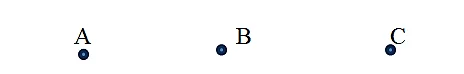
Обозначать точки в математике, принято большими буквами латиницы.

Произносится:точка А, точка В, точка С.

Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.

Одномерные фигуры

Одномерные фигуры это фигуры, у которых есть только одно измерение — длина. Эти фигуры могут быть представлены линиями или отрезками.

Примерами одномерных фигур являются:

• Отрезок — это часть прямой, которая ограничена двумя точками. Длина отрезка определяется расстоянием между этими точками.
• Линия — это бесконечно длинная фигура, состоящая из точек, которые лежат на одной прямой.
• Кривая — это линия, которая не является прямой и может иметь разные формы, такие как окружность, эллипс, парабола и другие.

Одномерные фигуры важны в математике и физике для описания перемещения и движения тел. Они также используются в геометрии для решения задач и построения различных графиков и диаграмм.

Отрезок: разные значения слова

Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке. Часто слово употребляется для характеристики временного промежутка — «отрезок времени»

Часто слово употребляется для характеристики временного промежутка — «отрезок времени»

Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.

Съем жилья или ипотека? Что выбрать? Считаем вместеКак хранить деньги почти без риска Семейный бюджет. Что это? Как правильно его вести и сэкономить?Как экономить воду в квартире с счётчиком?

Точки, прямые, отрезки

Чтобы изобразить прямую на листе бумаги необходимы карандаш и линейка (Рис.1). Причем, прямая не имеет начала и конца, то есть мы изображаем лишь часть прямой, но при этом можно дочертить прямую в одну из сторон, либо сразу в обе стороны.

Обозначать прямые принято малыми латинскими буквами (

Рис.2,
Рис.2бточки жебольшимиА, В, СРис.2

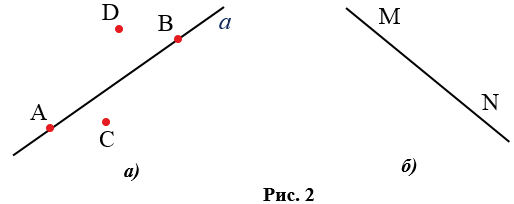
Возможны два варианта расположения точек относительно прямой:

Важно знать, что через любые две точки можно провести прямую и притом только одну. Если мы рассмотрим две прямые, то возможны два варианта расположения этих двух прямых друг относительно друга:

Если мы рассмотрим две прямые, то возможны два варианта расположения этих двух прямых друг относительно друга:

На Рис.5, под пунктом

)отрезком.концамиРис. 5б)АВАВВААВАВАВ

Сравнение отрезка с геометрическими фигурами

В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.

Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.

Луч — составная часть прямой, которая  ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.

Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.

Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.

Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.

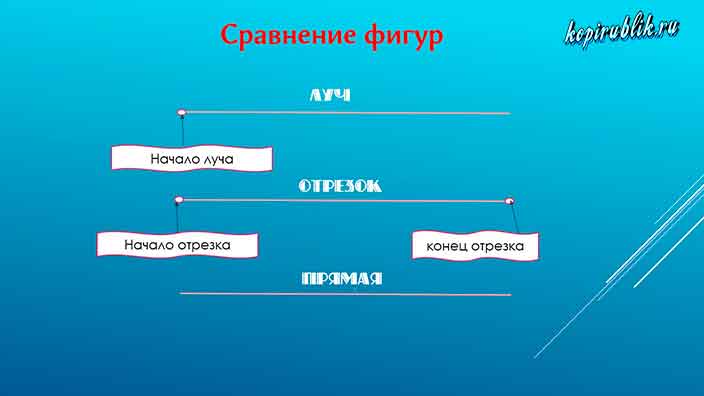
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:

1 точка — луч;

2 точки — отрезок;

Нет точек — прямая.

Минутка истории

В древней Греции существовали две идеальные фигуры – окружность, круг. Все точки окружности одинаковые между собой, это позволяет окружности самостоятельно совершать движение. Именно это свойство положило начало изобретения колеса. К огромному сожалению, изобретатель остался неизвестным. А модель колеса с того времени практически не изменилась.

Известно, что первые колеса появились в Месопотамии в 3000гг. до н.э. и использовались для изготовления гончарных изделий и колес для движения телег.

Почему так много внимания уделяется обычной геометрической фигуре? – спросите вы.

Давайте представим, что колесо просто не создано, его нет! А значит, нет совершенно никакого транспорта, не работают фабрики и заводы, не существуют механизмы. Человечество не двигается вперед. Жизнь остановилась!

Такое даже представить страшно!

Обозначение углов на чертеже

Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.

На чертеже запечатлено корректное обозначение острых, равных и неравных углов.

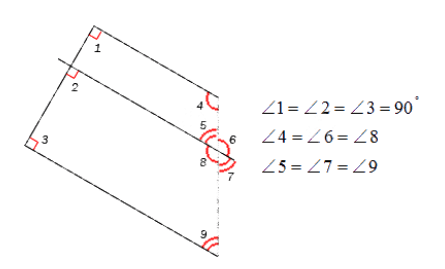
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.

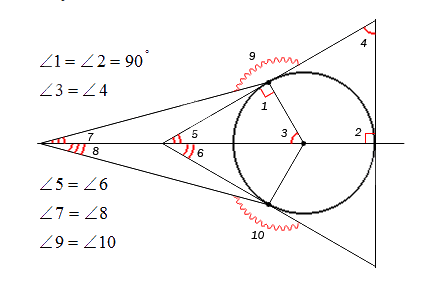
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.

Как измерить угол?

Для измерения углов используется транспортир:

Транспортир

Попробуем измерить угол \

Шаги для измерения угла \.

Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.

Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°

Далее попробуем измерить этот ∠AOC:

Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.

Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°

Аксиома 3

Ак­си­о­ма 3: через любые две точки про­хо­дит пря­мая, и при­том толь­ко одна.

По­яс­не­ние: мы мно­же­ство раз при­кла­ды­ва­ли ли­ней­ку к двум точ­кам и про­во­ди­ли от­ре­зок – часть пря­мой. Что го­во­рит ак­си­о­ма? Что через эти две точки про­хо­дит пря­мая, и при­том толь­ко одна. Вроде бы это по­нят­но. Но если одна точка на Земле, а вто­рая на Луне? Как про­ве­рить, одна пря­мая про­хо­дит или нет? Ли­ней­ку мы не про­ло­жим. Так вот, ак­си­о­ма утвер­жда­ет, что даже через эти две точки про­хо­дит толь­ко одна пря­мая! (см. рис. 3)

Рис. 3. Ак­си­о­ма 3 верна при боль­ших рас­сто­я­ни­ях

Дру­гой край­ний слу­чай: точки очень близ­ко рас­по­ло­же­ны друг к другу. Две пес­чин­ки. Если мы при­ло­жим ли­ней­ку, то до­воль­но труд­но про­ве­сти пря­мую. Так вот, ак­си­о­ма утвер­жда­ет: через любые две точки – и близ­кие, и да­ле­кие – про­хо­дит пря­мая, и при­том толь­ко одна (см. рис. 4).

Рис. 4. Ак­си­о­ма 3 верна при малых рас­сто­я­ни­ях

Далее изу­чим знак при­над­леж­но­сти.

Еще наши карточки Домана по методике «Вундеркинд с пеленок» :

1. Алфавит для детей по методике Домана
2. Комплект карточек «Буквы»
3. Карточки — Обучение чтению по Доману
4. Карточки Домана — Счёт от 1 до 20
5. Карточки Домана Цвета
6. Карточки Домана Овощи
7. Карточки Домана Ягоды
8. Карточки Домана Орехи 
9. Карточки Домана Фрукты
10. Карточки Домана Грибы
11. Карточки Домана Дикие животные
12. Карточки Домана Домашние животные и птицы
13. Карточки Домана Экзотические животные
14. Карточки Домана Птицы
15. Карточки Домана Амфибии и рептилии
16. Карточки Домана Насекомые
17. Карточки Домана Бабочки
18. Карточки Домана Породы кошек
19. Карточки Домана Породы собак
20. Карточки Домана Подводный мир и рыбы
21. Карточки Домана Цветы
22. Карточки Домана Полевые цветы -Травы
23. Карточки Домана Природа
24. Карточки Домана Явления природы
25. Карточки Домана Игрушки
26. Карточки Домана Детское творчество
27. Карточки Домана Бытовая техника
28. Карточки Домана Мебель
29. Карточки Домана Посуда
30. Карточки Домана Одежда
31. Карточки Домана Обувь
32. Карточки Домана Плоские геометрические фигуры
33. Карточки Домана Объемные геометрические фигуры
34. Карточки Домана Еда
35. Карточки Домана Десерты и выпечка
36. Карточки Домана Национальные блюда
37. Карточки Домана Напитки
38. Карточки Домана На прогулке
39. Карточки Домана Профессии
40. Карточки Домана Транспорт-1:Наземный транспорт
41. Карточки Домана Транспорт-2: Спецтехника
42. Карточки Домана Транспорт-3: Железнодорожный транспорт
43. Карточки Домана Транспорт-4: Воздушный транспорт
44. Карточки Домана Транспорт-5: Водный транспорт
45. Карточки Домана Спортинвентарь
46. Карточки Домана музыкальные инструменты
47. Карточки Домана Дом-Интерьер
48. Карточки Домана Дом-Личные вещи
49. Карточки Домана Дом-Бытовые предметы
50. Карточки Домана Математика
51. Карточки Домана Части тела
52. Карточки Домана Глаголы (действия)
53. Карточки Домана Достопримечательности России
54. Карточки Домана Достопримечательности мира
55. Карточки Домана Картины Великих художников
56. Карточки Домана Инструменты
57. Карточки Домана Космос
58. Карточки Домана «Что придумал человек»
59. Карточки Домана «Выдающиеся личности»
60. Суперкарточки по методике Домана «Вундеркинд с пеленок», набор — «Читаем на прогулке»
61. Суперкарточки по методике Домана «Вундеркинд с пеленок», набор — «Читаем на улице»
62. Суперкарточки по методике Домана «Вундеркинд с пеленок», набор — «Читаем в шкафу»
63. Суперкарточки по методике Домана «Вундеркинд с пеленок», набор — «Читаем в детской»
64. Суперкарточки по методике Домана Вундеркинд с пеленок, набор — «Читаем на кухне»
65. Суперкарточки по методике Домана Вундеркинд с пеленок, набор — «Читаем в доме»
66. БОЛЬШОЙ набор карточек Домана «Мои первые знания» для малышей от 6 месяцев до 1 года

Третий важный элемент геометрии — это поверхности

Поверхности, как и линии бывают разными, причем разнообразие поверхностей еще больше, чем линий.

3.1. Элементарная поверхность

Основная характеристика элементарной поверхности — площадь и вообще можно назвать элементарную поверхность элементарной частью площади. Для определения площади элементарной поверхности недостаточно знать только длину, необходимо оперировать еще и шириной. Таким образом элементарная поверхность — это уже элемент двухмерного мира. Как и линия, поверхность образована точками, минимум тремя, или линиями, как минимум тремя. Но с точки зрения классической геометрии это не совсем так. В геометрии Эвклида поверхность качественно новый элемент геометрии, связанный с предыдущими тем, что поверхность ограничивается линиями, поэтому определение поверхности как некоего элемента главная характеристика которого — площадь, вполне допустима.

3.2. Из элементарных поверхностей может слагаться поверхность сколь угодно большой площади

При этом как и в случае с линиями рассматривать все расстояния между точками вовсе не обязательно и даже расстояния между всеми линиями, которые могут быть образованы из этих точек — тоже не обязательно. Достаточно знать характеристики главных линий, я бы назвал эти линии характерными линиями. Характерные линии ограничивают поверхность, например черный квадрат Малевича ограничен 4 линиями.

3.3. Самая простая поверхность — плоская поверхность или как сейчас говорят — плоскость

Плоскость двухмерна, это означает, что плоскость всегда можно расположить так, что наблюдателю будет видна только одна линия. Например, плотники с древнейших времен проверяют точность обработки деревянного бруса, смотря на исследуемую поверхность так, чтобы линия, ограничивающая начало поверхности, совпала с линией, ограничивающей конец поверхности.

Плоскость — это частный случай всех возможных плоскостей, но как и прямая линия, плоскость очень важна для решения задач геометрии. Более того, прямая линия и плоскость интуитивно понятны даже людям, никогда геометрию не изучавшим. Например, когда человеку нужно добраться из точки А в точку В, то он старается проложить маршрут, максимально близкий к прямой линии, а если путь будет проходить по равнине, а не по пересеченной местности, то совсем хорошо. А еще люди делают тоннели в горах и засыпают овраги, чтобы сделать дорогу из одного пункта в другой максимально приближающейся к прямой линии.

И точка и линия и поверхность в геометрии могут рассматриваться и как отдельные элементы и как формообразующие элементы, например, точка формообразующий элемент для линии, а линия формообразующий элемент для поверхности. Также точка, линия и поверхность могут быть общими элементами геометрических фигур.

Для основной части школьного курса геометрии этих элементов вполне достаточно, да и у Евклида трехмерные геометрические фигуры рассматриваются в книгах XI-XIII. Тем не менее хочется закончить этот ряд.

Цилиндр и его свойства

Цилиндр – геометрическое тело, образованное двумя параллельными плоскостями, основаниями, и боковой поверхностью, являющейся цилиндрической поверхностью. Основания цилиндра имеют форму круга, а боковая поверхность представляет собой цилиндрическую оболочку между основаниями.

У цилиндра есть несколько свойств:

• Объем: объем цилиндра равен произведению площади основания на высоту. Формула для расчета объема цилиндра: V = πr2h, где π – математическая константа, r – радиус основания, h – высота цилиндра.
• Площадь боковой поверхности: площадь боковой поверхности цилиндра рассчитывается по формуле: Sб = 2πrh, где h – высота цилиндра, r – радиус основания.
• Площадь полной поверхности: площадь полной поверхности цилиндра складывается из площади двух оснований и боковой поверхности. Формула для расчета: Sп = 2πr2 + 2πrh.

Цилиндры используются в различных областях, например, для создания баков, цистерн, трубопроводов, а также в архитектуре, механике и других отраслях науки.

Эллипс и его свойства

Эллипс – это геометрическая фигура, которая получается пересечением плоскости и конуса, если плоскость не проходит через вершину конуса.

Если взять две оси, одну большую и одну меньшую, то эллипс будет выглядеть как овал, причем центр овала совпадает с центром эллипса.

У эллипса есть ряд свойств, которые помогают описать его положение и размеры:

• Фокусы – точки, через которые проходят оси эллипса. Если провести линию от одного фокуса до любой точки эллипса и продолжить ее до пересечения с другой осью, то расстояние от точки пересечения до второго фокуса будет равно расстоянию от этой точки до первого фокуса.
• Большая и меньшая полуоси – это половина большей и меньшей оси, соответственно.
• Эксцентриситет – это число, которое характеризует степень сжатия эллипса относительно его формы. Чем выше эксцентриситет, тем более овальной будет форма эллипса.

Эллипс имеет много применений, от геометрии и физики до создания красивых дизайнов. Его свойства используются в проектировании спутниковых орбит, определении траекторий космических кораблей, строительстве зданий и мостов, а также в дизайне создания эстетических форм для скульптур и других произведений искусства.