Шар и сфера

Примеры решения задач

Задача 1

Геометрическое тело шарообразной формы обладает объемом, равным \(\frac{36}{\sqrt\pi}\). Необходимо вычислить значение поверхностной площади объекта при условии увеличения его радиуса на величину \(\frac{6}{\sqrt\pi}\).

Решение

При известном радиусе и объеме шара достаточно просто определить значение поверхностной площади заданной фигуры. С этой целью нужно вспомнить соответствующие формулы из курса теории. Применим эти уравнения к условиям задачи и выполним необходимые вычисления:

\(V_{\text{шара}} = \frac{4}{3}\pi R^3 = \frac{36}{\sqrt\pi} \Rightarrow R = \frac{3}{\sqrt\pi}\)

Найдем радиус полученного шара:

\(R_{\text{нов.}} = R + \frac{6}{\sqrt\pi} = \frac{9}{\sqrt\pi}\)

Далее остается лишь путем подстановки найденных значений в стандартную формулу определить искомую площадь поверхности:

\(S_{\text{пов.}} = 4\pi R_{\text{нов.}}^2 = 4\pi \left(\frac{9}{\sqrt\pi}\right)^2 = 4\pi\frac{81}{\pi} = 324\)

Ответ: \(S_{\text{пов.}} = 324\)

Задача 2

Дана шарообразная фигура. Необходимо вычислить, в какое количество раз объем этого объекта превышает аналогичные параметры фрагмента с высотой, равной половине радиуса.

Решение

В процессе решения задачи потребуется найти частное от деления объема шара на объем обозначенного в условии сегмента. Высоту рассматриваемого фрагмента допустимо выразить с помощью следующего уравнения:

\(H = \frac{1}{2}R\)

Далее воспользуется стандартными формулами, знакомыми из теоретического курса стереометрии, и выполним соответствующие расчеты:

\(\frac{V_{\text{шара}}}{V_{\text{сегм.}}} = \frac{\frac{4}{3}\pi R^3}{\pi \left(\frac{1}{2}R\right)^2\left(R — \frac{1}{3}\left(\frac{1}{2}R\right)\right)} = \frac{\frac{4}{3}\pi R^3}{\frac{5}{24}\pi R^3} = \frac{4}{3} \cdot \frac{24}{5} = \frac{32}{5} = 6,4\)

Ответ: 6,4

Задача 3

На рисунке ниже изображена пара сфер, отличающихся по размеру. Радиус первой фигуры в два раза превышает аналогичные параметры второго объекта. Вторая сфера целиком погружена в пространство, ограниченное первой сферической фигурой. При условии, что объем шара, который расположен внутри второй сферы составляет \(V_2\),  объем объекта, расположенного между сферами соответствует V. Требуется вычислить соотношение \(V : V_2\).

Решение

Представим, что \(V_1\) представляет собой объем шарообразной фигуры, которая ограничена первой сферой. Исходя из того, что радиус \(S_1\) в два раза превышает значение радиуса \(S_2\), целесообразно записать следующее соотношение:

\(V_1 : V_2 = 8\)

Таким образом:

\(V = V_1 — V_2 = 8V_2 — V_2 = 7V_2\)

В результате получим:

\(V : V_2 = 7\)

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений

Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении

Одно из таких базовых понятий — это геометрическая точка. Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Сфера

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы»

Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

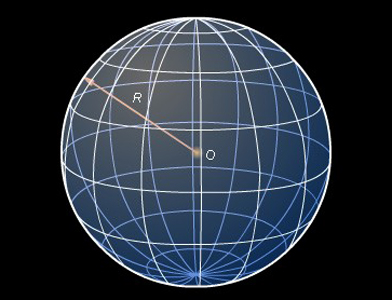
Сфера и радиус сферы

Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

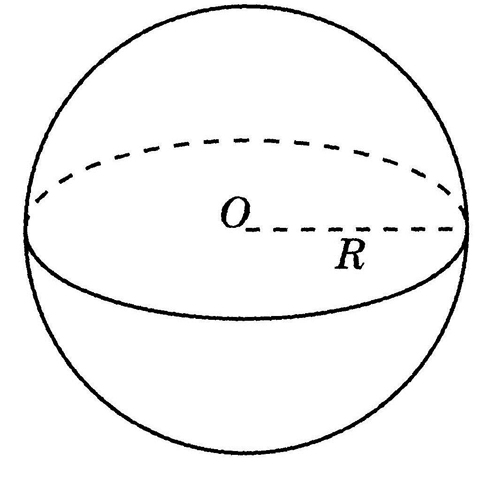
Шар

Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.

Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Понятие сферы и шара

Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.

Важно отличать шар от сферы. Сферой называют только поверхность шара

Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.

Дадим строгие определения сферы и шара:

Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.

Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:

Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.

Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:

Касательная, касательная плоскость к сфере и их свойства

Определение.
Касательная к сфере
— это прямая, которая касается сферы только в одной точке.

Определение.
Касательная плоскость к сфере
— это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение.
Сегмент шара
— это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента
называют круг, который образовался в месте сечения. Высотой сегмента
h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула.
Площадь внешней поверхности сегмента сферы
с высотой h
через радиус сферы R:

S = 2π
Rh

Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Поверхность планеты Земля

Формулу сферы можно применить для определения на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:

• Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно. Отличие между этими цифрами не превышает 0,3%, поэтому для расчета можно взять средний радиус 6371 км.
• Во-вторых, рельеф является трехмерным, то есть на ней имеются впадины и горы. Эти характерные особенности планеты приводят к увеличению ее площади поверхности, тем не менее, в расчете их учитывать не будем, поскольку даже самая большая гора, Эверест, составляет 0,1% от земного радиуса (8,848/6371).

Используя формулу сферы, получаем:

Россия, по официальным данным, занимает площадь 17,125 млн км 2 , что составляет 3,36% от поверхности планеты. Если же учесть, что к суше относятся лишь 150,387 млн км 2 , тогда площадь нашей страны составит 11,4% от всей территории, не покрытой водой.

Понятие сферы и шара

Если оглядеться вокруг, то можно найти множество шарообразных и сферических объектов в окружающем мире. Такая форма характерна для космических тел, в том числе, нашей планеты. С мячами разнообразных размеров, фактур и цветов люди встречаются во время занятий спортом и на игровых соревнованиях. Многие фрукты и овощи обладают круглой формой. Подобные примеры касаются реальной жизни. В рамках курса стереометрии перечисленные понятия отличаются

Важно уметь разбираться в терминологии и отличать фигуры друг от друга по ряду характерных признаков

Сферой называют поверхность, в состав которой входит совокупность точек, равноудаленных от какой-то одной центральной точки, называемой центром.

Шар представляет собой материальное тело, в состав которого включены все точки в пространственном измерении, расстояние от которых до определенной центральной точки не более чем заданная величина.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

При рассмотрении вышеуказанных понятий часто встречается определение радиуса. Под ним подразумевают прямую, ограниченную парой точек, одна из которых лежит на сфере, а вторая — представляет собой центр этой фигуры. Кроме того, аналогичный отрезок играет роль радиуса шара, помещенного во внутреннее пространство анализируемой сферической фигуры. Наглядно представить эти понятия несложно, если обратиться к изображению, расположенному ниже на рисунке:

Другое важное понятие касается диаметра сферы. Такое название присуще отрезку, пересекающему центральную точку сферической фигуры

При этом начало и конец данной линии расположены на рассматриваемой сфере. Непосредственно сфера является фрагментом шара. Существует аналогичное утверждение, когда окружность признают частью круга. Исходя из расшифровки термина сферы, можно сформулировать справедливое заключение о равенстве радиусов этой фигуры.

Таким образом, центральная точка сферической фигуры делит диаметр пополам. В свою очередь, диаметр сферы в два раза превышает размер радиуса аналогичного объекта. Кроме того, сфера представляет собой тело вращения. Из данного определения можно сделать вывод о способе получения сферической фигуры. Достаточно лишь повернуть половину окружности относительно ее диаметра, чтобы образовалась сфера.

Трехмерное пространство

Большая часть геометрических построений производится в плоскости, но в старших классах начинают изучать трехмерные фигуры. Двухмерное пространство имеет только две характеристики: длину и ширину. В трехмерных областях добавляется высота. В математике 6 класса изучаются отдельные 3д фигуры.

На плоскости фигуру характеризовала площадь и периметр. В трехмерных объектах к ним прибавляется объем.

Рис. 1. Трехмерное пространство.

Кроме того, имеется ряд специфических свойств 3д фигур. Их может пересекать прямая и плоскость, могут имеется секущие плоскости, которые принимают формы других фигур.

Применение 3д фигур для составления задач значительно усложняет их, но в то же время делает куда более интересными. Приведем определения шара и сферы, после чего попробуем выделить различия этих фигур.

Разветвление: теорема о касательной плоскости к сфере

Ка­са­тель­ной плос­ко­стью к сфере на­зы­ва­ют такую плос­кость, ко­то­рая имеет со сфе­рой ровно одну общую точку. Их общая точка на­зы­ва­ет­ся точ­кой ка­са­ния плос­ко­сти и сферы.

Рис. 4. Ра­ди­ус, про­ве­ден­ный в точку ка­са­ния	Рис. 5. Ил­лю­стра­ция к до­ка­за­тель­ству тео­ре­мы

Тео­ре­ма: ра­ди­ус сферы  (рис. 4), про­ве­ден­ный в точку ка­са­ния сферы и плос­ко­сти, пер­пен­ди­ку­ля­рен ка­са­тель­ной плос­ко­сти.

До­ка­за­тель­ство от про­тив­но­го: пред­по­ло­жим, что ра­ди­ус  про­ве­ден­ный в точку ка­са­ния, не пер­пен­ди­ку­ля­рен плос­ко­сти. Тогда про­ве­дем пер­пен­ди­ку­ляр  к дан­ной плос­ко­сти (рис. 5). Тогда рас­сто­я­ние  будет мень­ше, чем , так как  – на­клон­ная, а  – пер­пен­ди­ку­ляр. Из этого сле­ду­ет, что точка  лежит внут­ри сферы, так как  мень­ше ра­ди­у­са . А это зна­чит, что име­ет­ся еще одна точка пе­ре­се­че­ния сферы и плос­ко­сти, что яв­ля­ет­ся про­ти­во­ре­чи­ем. Зна­чит, ис­ход­ное пред­по­ло­же­ние невер­но и ра­ди­ус  пер­пен­ди­ку­ля­рен ка­са­тель­ной плос­ко­сти.

Об­рат­ная тео­ре­ма: если ра­ди­ус сферы пер­пен­ди­ку­ля­рен плос­ко­сти, про­хо­дя­щей через его конец, ле­жа­щий на сфере, то эта плос­кость яв­ля­ет­ся ка­са­тель­ной.

До­ка­за­тель­ство: раз ра­ди­ус пер­пен­ди­ку­ля­рен плос­ко­сти, то рас­сто­я­ние от цен­тра сферы до плос­ко­сти равно ра­ди­у­су, а тогда плос­кость и сфера имеют ровно одну общую точку. Зна­чит, по опре­де­ле­нию, эта плос­кость и есть ка­са­тель­ная.

Пересечение двух сфер

Пусть есть две пересекающиеся сферы с центрами в точках О₁ и О₂ с радиусами R₁ и R₂ соответственно. Какую форму будет иметь линия L, по которой они пересекаются?

Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:

Проведем радиусы О₁А, О₁В, О₂А и О₂В. Теперь сравним ∆АО₁О₂ и ∆ВО₁О₂. Сторона О₁О₂ у них общая, а другие стороны попарно равны как радиусы сфер:

Получается, что ∆АО₁О₂ и ∆ВО₁О₂ равны. Теперь из точек А и В опустим высоты на прямую О₁О₂. Из равенства ∆АО₁О₂ и ∆ВО₁О₂ вытекает два факта:

• эти высоты упадут в одну точку Н;
• эти высоты будут одинаковы, то есть АН = НВ.

Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О₁О₂ – перпендикуляр к плоскости окружности, ведь О₁О₂⊥АН и О₁О₂⊥ВН.

Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:

Теперь сравним ∆О₁НС и ∆О₁НА. Они прямоугольные, ведь О₁Н – перпендикуляр к плос-ти окружности. Катет О₁Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О₁НС и ∆О₁НА равны, и потому

Это равенство означает, что С принадлежит сфере с центром в О₁. Аналогично рассмотрев ∆О₂НС и ∆О₂НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.

Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.

Отметим ещё один факт: по неравенству треугольника отрезок О₁О₂ должен быть меньше суммы отрезков О₁А и О₂А, то есть суммы радиусов сфер.

Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.

Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:

Трактовка значений

Это следует знать:

• Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
• Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
• Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
• Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
• Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
• Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
• Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Свойства

Из курса геометрии известно, что при решении задач на вычисление параметров или начертание разнообразных фигур целесообразно использовать их свойства. В случае со сферическими объектами этот метод не менее эффективен. Сфера обладает рядом специфических свойств, знание которых значительно упрощает и ускоряет решение многих примеров из стереометрии. Перечислим основные из них:

1. Какое-либо сечение шара с помощью плоскости позволяет получить геометрическую фигуру в виде круга.
2. Какое-либо сечение шарообразного предмета, выполненное посредством некоторой плоскости, имеет круглую форму.
3. При выборе любого сечения сферического объекта в результате получается окружность.
4. Каждая из точек, принадлежащих сфере, находится на одинаковом расстоянии от ее центральной точки.
5. Сфера обладает максимальным объемом по сравнению с прочими фигурами в пространственном измерении, которые характеризуются идентичными поверхностными площадями.
6. Через пару произвольных диаметрально противоположных точек, которые расположены на наибольшем удалении друг от друга и принадлежат одной окружности, допустимо построить любое число кругов для шара или окружностей для сфер радиусом, соответствующим радиусу рассматриваемого шара или сферы.

Примечание 1

Обращаясь к последнему свойству, характерному для сферического объекта, стоит записать важное замечание. В том случае, когда точки не являются диаметрально противоположными, представляется возможным выполнить построение единственного круга или окружности

Площади сферы и ее частей. Объемы шара и его частей

В следующей таблице приведены формулы для расчета объема сферы и объемов ее частей, а также площади сферы и площадей ее частей.

Фигура	Рисунок	Формула	Описание
Прохладный		S = 4πr2, где r — радиус сферы.	Диапазон пуль
Мяч	где r — радиус шара.	Объем мяча
Сферический ремень		S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !	Площадь сферического пояса
Мяч команда	где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.	Объем сферического слоя
Сферический сегмент		S = 2пр, где r — радиус сферы, h – высота сферического сегмента.	Площадь сферического сегмента
Шаровой сегмент	где r — радиус шара, h – высота сферического сегмента.	Объем сферического сегмента
Сектор мяча		где r — радиус шара, h — высота сферического сектора.	Объем сферического сектора

Прохладный

Диапазон мяча: S = 4πr2, где r — радиус сферы.

Мяч

Объем мяча: где r — радиус шара.

Сферический ремень

Площадь сферического пояса: S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !

Мяч команда

Объем шаровой кровати: где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.

Сферический сегмент

Площадь сферического сегмента: S = 2пр, где r — радиус сферы, h – высота сферического сегмента.

Шаровой сегмент

Объем шарового сегмента: где r — радиус шара, h – высота сферического сегмента.

Сектор мяча

Объем сектора сферы: где r — радиус шара, h — высота сферического сектора.

Сфера и шар

Организация: ГБПОУ Уфимский политехнический колледж

Населенный пункт: Республика Башкортостан, г. Уфа

Цель урока: рассмотреть понятия «сфера» и «шар», выяснить их сходства и различия, познакомиться с формулами площади сферы и объёма шара и научиться применять их при решении задач. Рассмотреть примеры сферы и шара, которые можно встретить в окружающем мире.

Задачи урока: 1)совместное исследование и решение задач,

2)теоретическое изучение формул площади сферы и объема шара, посмотреть мастер-класс по приготовлению сферы из шоколада

3) организовать самостоятельную деятельность обучающихся в процессе обучения.

Тип урока Урок изучения нового материала

Формируемые результаты

Предметные: обобщить понятия сферы и шара, нахождение площади сферы и объема шара

Личностные: формировать ответственное отношение к учению, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию.

Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.

Планируемые результаты

Обучающиеся узнают формулы для вычисления площади сферы и объема шара, научатся применять формулы при решении задач, выявят связь между элементами сферы и шара.

Организационная структура урока

Этапы урока	Деятельность преподавателя	Деятельность обучающихся
1. орг. момент	Приветствие. Слайд 1
2.Актуализация мыслительной деятельности	Изображена окружность с центром вт.О. Дать опр.окружности. Слайд.2 Дать опр. радиуса и диаметра. Слайд 3 На слайде появляется крут. Слайд 4 -В чем разница между кругом и окружностью? На слайде- кольца,монета,бублики,зеркало и т.д. Предложите задание к этим картинкам — А арбуз и мыльные пузыри где? Сделайте анализ. Какие тела они вам напоминают? — Записываем тему урока. Слайд 8	Отвечают на поставленные вопросы — Круг представляет собой не только окружность, которая явл. его границей, но и то, что внутри Обсуждают, предлагают разделить на 2 группы: окружность и круг. Слайд 6 Сфера и шар
3.Постановка учебной деятельности	— Какая цель нашего урока? Дополняет: познакомить с формулами площади сферы и объема шара. Рассмотреть примеры сферы и шара, которые можно встретить вокруг нас	— Рассмотреть понятия «сфера» и «шар», выяснить сходства и различия
4.Совместное исследование и решение учебной задачи 4.1 Теоретическое изучение основных понятий 4.2 Изучение формул объема шара и площади сферы 4.3 Практическое применение формул	Слайд 8. – Посмотреть на строение Земли. Какую фигуру напоминает? Слайд 9. –Шар из ниток Работа с учебником: выписываем определения. Слайды 10 и 11 — Записать формулы в тетради. Слайд 12 — Зачем используются эти формулы? Научимся применять эти формулы Слайд 13	— Шар — Сфера Выписывают определения со слайдов или с доски Записывают формулы — Для вычисления объема шара и площади сферы Решают задачи в тетрадях и у доски. Проверяют ответы Слайд 14
5.Связь с профессией	Сфера в повседневной жизни Слайд 15. Сфера в архитектуре Слайд 16 Сфера в астрономии Слайд 17 Просмотр мастер-класса «Моделирование сферы из шоколада» Слайд 18 (https://disk.yandex.ru/i/KloV1LHV4M7Iww)	Смотрят слайды, приводят свои примеры
6. Применение знаний	Проведем практическую работу. По результатам измерений в мастер-классе найти массу шоколада для каждой сферы. Класс разбивается на 3 группы. На слайдах формулы нахождения плотности Слайд 19, массы Слайд 20 и таблица плотности шоколада Слайд 21	1.Записывают измерения в тетради. D1=8см, D2= 4см и D3= 2см. 2. Вычисляют объем 3. Находят массу (Значения плотности берут из таблицы, )
7.Контроль и самопроверка	— А теперь проверим, как вы усвоили сегодняшний материал. Перед вами формулы, дайте им названия. Слайд 22	Ставят соответствие
8.Подведение итогов. Рефлексия.	— Теперь подведем итог, что мы сегодня повторили, что нового узнали и чему научились. Слайды 23, 24,25	Рассказывают определения, формулы
9. Инструктаж по выполнению домашнего задания	— Записываем домашнее задание Слайд 26	Записывают в тетрадях, задают вопросы, если есть
10.Завершение	Преподаватель благодарит за работу на уроке. Выставляет оценки. Слайд 27. (Резерв 28,29)	Ученики благодарят за урок.

Дополнительный видеоматериал см. https://disk.yandex.ru/i/KloV1LHV4M7Iww

Приложения:

1. file1_9b9ba280-f434-4437-8.. 24,2 МБ

2. file0.docx.. 23,3 КБ

Опубликовано: 15.03.2021

Доказательство и вывод уравнений

Введем декартовы координаты x, y, z и возьмем ось тела за ось x. Плоскость x пересекает поверхность тела по линии, где ось x является осью симметрии. Пусть y=f(x) — уравнение части прямой, расположенной над осью.

Проведем через точку х на оси абсцисс перпендикулярную ей плоскость и обозначим через V(x) объем части тела, лежащей левее этой плоскости, тогда V(x) есть функция от x . Найдем его производную: V'(x)=limh→0V(x+h)-V(x)h.

Разность V(x+h)-V(x) представляет собой объем слоя тела толщиной h между двумя плоскостями, перпендикулярными оси x, которые проходят через точки с абсциссами x и (x+h). Пусть M — наибольшее, а m — наименьшее значение функции f(x) на отрезке x, x+h. Тогда рассматриваемый слой тела содержит цилиндр радиуса m, высоты h и содержится в цилиндре радиуса M и той же высоты h, поэтому: πm2h≤V(x+h)-V(x)≤πM2h, πm2 ≤V (x+h)-V(x)h≤πM2.

Если f(x) — непрерывная функция, то левая и правая части последнего неравенства при h→0 будут стремиться к одному и тому же пределу πf2(x). Связь между ними стремится к тому же пределу, т.е производной V'(x)=πf2(x).

Формула 5

Согласно формуле анализа: V(b)-V(a)=∫abπf2(x)dx, a

Формула 6

Уравнение сферической поверхности x2+y2=R2.

Полуокружность над осью x задается уравнением: y=f(x)=R2-x2, -R≤x≤R. Следовательно, объем сферического слоя между плоскостями x=a и x=b определяется по формуле: V=V(b)-V(a)=π∫abR2-x2dx=πR2(ba)-π8b3-a3.

В качестве объема всего шара возьмите a=-R, b=R. Тогда получим объем сферы: V=43πR3.

Чтобы получить объем сегмента сферы высотой H, надо взять a=RH, b=R. Получаем объем сферического сегмента: V=πH2R-H3.

Презентация по предмету «Математика» на тему: «СФЕРА И ШАР. План презентации: Определение сферы, шара. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы. Итог урока.». Скачать бесплатно и без регистрации. — Транскрипт:

1

СФЕРА И ШАР

2

План презентации: Определение сферы, шара. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы. Итог урока.

3

Окружность и круг d r Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точки. r – радиус d – диаметр r Кругом называется часть плоскости, ограниченная окружностью.

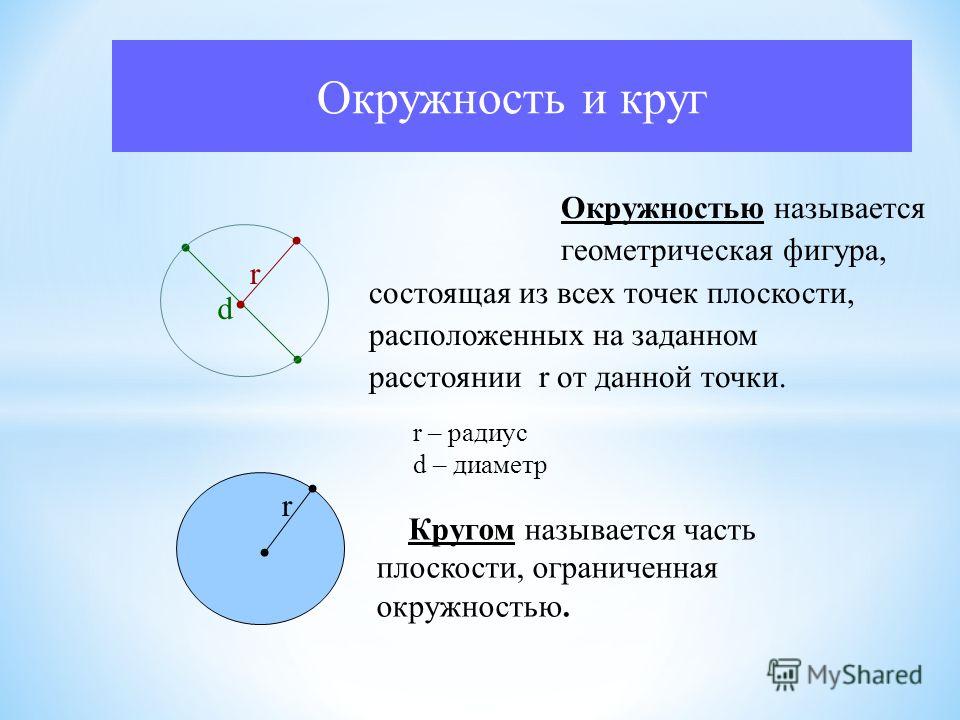
4

Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от данной точки (центра т.О). D О R – радиус сферы – отрезок, соединяющий любую точку сферы с центром. D – диаметр сферы – отрезок, соединяющий любые 2 точки сферы и проходящий через центр. т. О – центр сферы R

5

Шар Шаром называется тело, ограниченное сферой. Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара. Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.

6

Уравнение окружности О С(х 0 ;у 0 ) М(х;у) Зададим прямоугольную систему координат Оxy Построим окружность c центром в т. С и радиусом r Расстояние от произвольной т.М(х;у) до т.С вычисляется по формуле: МС = (x – x 0 ) 2 + (y – y 0 ) 2 МС = r, или МС 2 = r 2 Следовательно, уравнение окружности имеет вид: (x – x 0 ) 2 + (y – y 0 ) 2 = r 2

7

Уравнение сферы Зададим прямоугольную систему координат Оxyz z х у М(х;у;z) R C(x 0 ;y 0 ;z 0 ) Построим сферу c центром в т. С и радиусом R МС = (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2 МС = R, или МС 2 = R 2 Следовательно, уравнение сферы имеет вид: (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2 = R 2

8

Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы. Решение: так как уравнение сферы с радиусом R и центром в точке С(х 0 ;у 0 ;z 0 ) имеет вид (х-х 0 ) 2 + (у-у 0 ) 2 + (z-z 0 ) 2 =R 2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы (x-2) 2 + (y+3) 2 + z 2 =25 Ответ: (x-2) 2 + (y+3) 2 + z 2 =25

9

Взаимное расположение окружности и прямой Возможны 3 случая: d d r Если d r, то прямая и окружность не имеют общих точек.

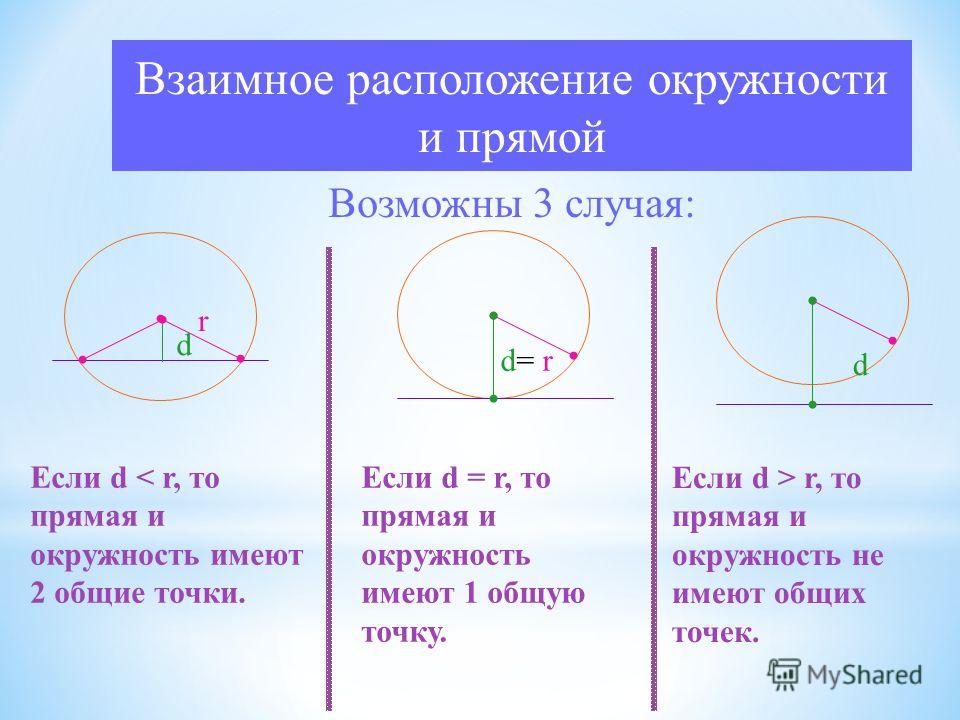
10

Взаимное расположение сферы и плоскости α C (0;0;d) х у z O Введем прямоугольную систему координат Oxyz Построим плоскость α, совпадающую с плоскостью Оху Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d — расстояние (перпендикуляр) от центра сферы до плоскости α. R

11

α Взаимное расположение сферы и плоскости C (0;0;d) х у z O r М Рассмотрим 1 случай: d

12

α Взаимное расположение сферы и плоскости C (0;0;d) х у z O Рассмотрим 2 случай: d = R, т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют одну общую точку

13

Взаимное расположение сферы и плоскости α х у z O C (0;0;d) Рассмотрим 3 случай: d > R, т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

14

Задача 2. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти радиус сечения. М К О R d Дано: Шар с центром в т.О R=41 дм α — секущая плоскость d = 9 дм Найти: r сеч = ? Ответ: r сеч = 40 дм

15

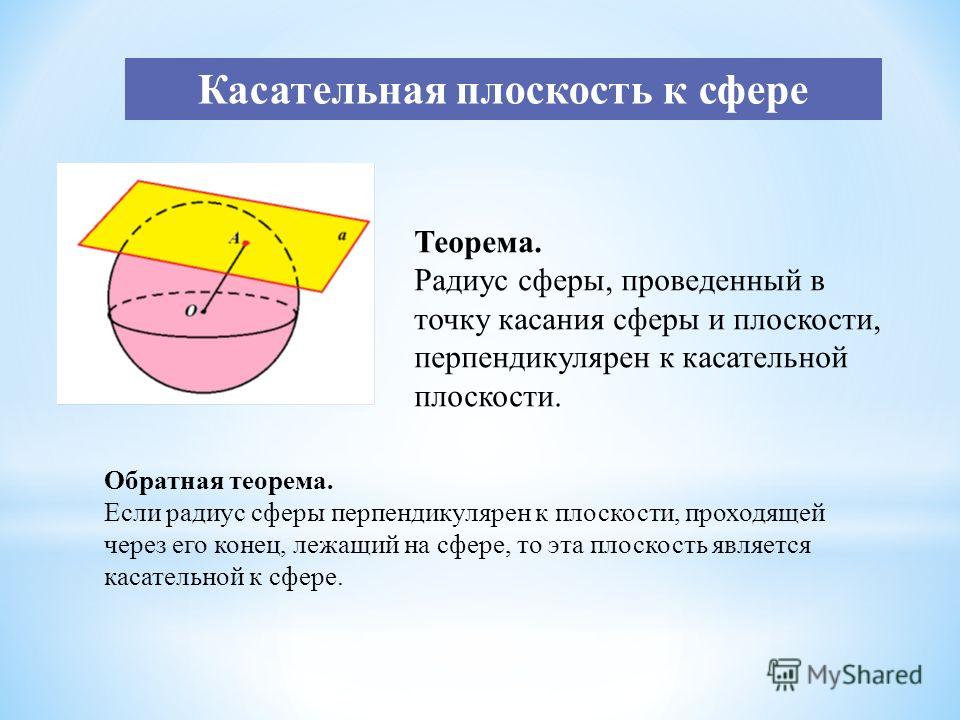
Касательная плоскость к сфере Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Обратная теорема. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

16

Площадь сферы и шара Сферу нельзя развернуть на плоскость. Опишем около сферы многогран ник, так чтобы сфера касалась всех его граней. За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани Площадь сферы радиуса R: S сф =4 π R 2 S шара =4 S круга т.е.: площадь поверхности шара равна учетверенной площади большего круга

17

Задача 3. Найти площадь поверхности сферы, радиус которой равен 6 см. Дано: сфера R = 6 см Найти: S сф = ? Решение: 1.S сф = 4πR 2 2.S сф = 4π 6 2 = 144π см 2 Ответ: S сф = 144π см 2

18

Итог урока: Сегодня вы познакомились с: определением сферы, шара; уравнением сферы; взаимным расположением сферы и плоскости; площадью поверхности сферы. Спасибо за работу!