Стереометрия

Содержание

• Слайд 1

  Урок 1
  Тема:
  «Предмет стереометрии.
  Аксиомы стереометрии.»

• Слайд 2

  — Что такое геометрия?
  Геометрия – наука о свойствах геометрических фигур
  «Геометрия» — (греч.) – «землемерие»
  — Что такое планиметрия?
  Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости.

  А
  а
  Основные понятия планиметрии:
  точка
  прямая
  — Основные понятия планиметрии?

• Слайд 3

  Стереометрия
  — раздел геометрии, в котором изучаются свойства фигур в пространстве

• Слайд 4

  Основные фигуры в пространстве:
  точка прямая плоскость

  α
  β
  Обозначение: А; В; С; …; М;…
  а

  А
  В
  М
  N
  Р

  Обозначение: a, b, с, d…, m, n,…(или двумя заглавными латинскими)
  Обозначение: α, β, γ…
  Ответьте на вопросы по рисунку:
  1. Назовите точки, лежащие в плоскости β; не лежащие в плоскости β.
  2. Назовите прямые, лежащие в плоскости β; не лежащие в плоскости β

• Слайд 5

  Некоторые геометрические тела.

  А
  В
  С
  Д
  Д1
  С1
  В1
  А1
  куб

  А
  В
  С
  Д
  А1
  В1
  С1
  Д1
  параллелепипед

  А
  В
  С
  Д
  тетраэдр

  цилиндр

  конус

• Слайд 6

  Назовите какие геометрические тела вам напоминают предметы, изображенные на этих рисунках:
  Назовите предметы из окружающей вас обстановки ( нашей классной комнаты) напоминающие вам геометрические тела.

• Слайд 7

  Практическая работа.
  1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром).

  2. Обозначьте вершины куба заглавными буквами АВСДА1В1С1Д1
  А
  В
  С
  Д
  Д1
  С1
  В1
  А1
  3. Выделите цветным карандашом:
  вершины А, С, В1, Д1
  отрезки АВ, СД, В1С, Д1С
  диагонали квадрата АА1В1В

• Слайд 8

  — Что такое аксиома?
  Аксиома – это утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.
  Аксиомы планиметрии:
  — через любые две точки можно провести прямую и притом только одну.
  из трех точек прямой одна, и только одна, лежит между двумя другими.
  имеются по крайней мере три точки, не лежащие на одной прямой…

• Слайд 9

  Аксиомы стереометрии.

  А
  В
  С
  А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.
  α

• Слайд 10

  Если ножки стола не одинаковы по длине, то стол стоит на трех ножках, т.е. опирается на три «точки», а конец четвертой ножки (четвертая точка) не лежит в плоскости пола, а висит в воздухе.

• Слайд 11

  Аксиомы стереометрии.

  А
  В
  α
  А2.Если две точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости.
  Говорят: прямая лежит в плоскости или плоскость проходит через прямую.

• Слайд 12

  а

  М
  Прямая лежит в плоскости
  Прямая пересекает плоскость
  Сколько общих точек имеют прямая и плоскость?

• Слайд 13

  Аксиомы стереометрии.

  α
  β
  А3.Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят: плоскости пересекаются по прямой.
  А
  а

• Слайд 14

  Решить задачи: №1(а,б); 2(а)

  А
  В
  С
  Д
  Р
  Е
  К
  М

  А
  В
  С
  Д
  А1
  В1
  С1
  Д1

  Q

  P

  R
  К
  М
  Назовите по рисунку:
  а) плоскости, в которых лежат прямые РЕ, МК, ДВ, АВ, ЕС; б) точки пересечения прямой ДК с плоскостью АВС, прямой СЕ с плоскостью АДВ.
  а) точки, лежащие в плоскостях ДСС1 и ВQС

• Слайд 15

  Подведем итоги урока:
  1) Как называется раздел геометрии, который мы будем изучать в 10-11 классах?
  2) Что такое стереометрия?
  3) Сформулируйте с помощью рисунка аксиомы стереометрии, которые вы изучили сегодня на уроке.

  А
  А
  В
  В
  α
  α

  А
  α
  β

• Слайд 16

  Домашнее задание:
  Повторить аксиомы планиметрии
  Выучить аксиомы А1-А3
  Прочитать пункт 1,2 (стр. 3 – 6)
  Решить задачи: 1(в,г); 2(б,д).
  Дополнительно: № 3; 4 ( по желанию)

Посмотреть все слайды

Простейшие следствия из аксиом стереометрии

На основе аксиом можно доказать несколько простых теорем стереометрии.

Доказательство. Возьмем произвольную прямую m и точку C, которая НЕ принадлежит m. Далее отметим на m две любые точки и обозначим их как А и В:

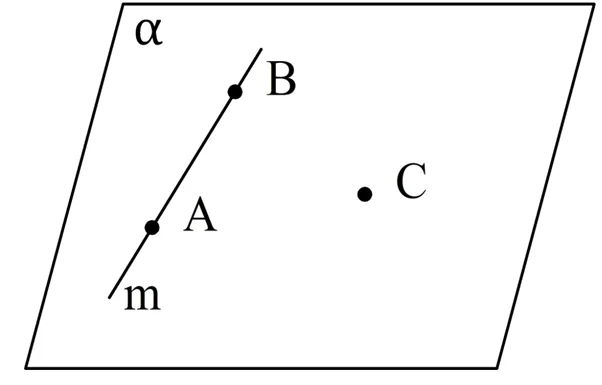
По аксиоме 1 через А, В, С можно провести некоторую плос-ть α. По аксиоме 4 прямая m будет принадлежать α. Тем самым мы показали, что существует плос-ть, проходящая через m и C. Единственность этой плос-ти вытекает уже из аксиомы 2, ведь через А, В и С нельзя провести две различных плос-ти, ч. т. д.

Иногда доказанный факт формулируют иначе: прямая и точка, не находящаяся на прямой, однозначно определяют проходящую через них плос-ть. То есть, указав прямую и точку, можно одновременно указать на ту плос-ть, которая задается ими.

Переходим к следующей теореме.

Отметим на произвольной прямой m точки А и В. Далее выберем ещё две точки в пространстве C и D, причем такие, что А, В, С и D не находятся в одной плос-ти. Тогда у нас есть плос-ти АВС и АВD, которые пересекаются по прямой АВ:

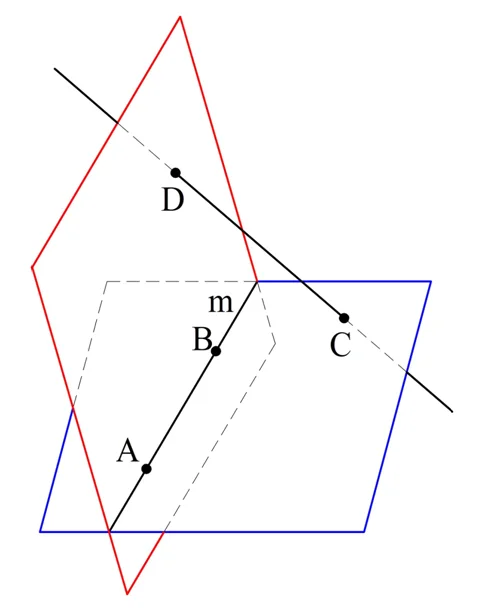
Теперь соединим С и D прямой. Прямая CD состоит из бесконечного количества точек. Через каждую из них можно провести единственную плос-ть, которая будет проходить через АВ. Так как точек бесконечно много, то и плос-тей будет бесконечно много. Осталось лишь показать, что никакие две таких плос-ти не будут совпадать, то есть все они различны.

Действительно, пусть две таких плос-ти совпадают, то есть на самом деле являются одной плос-тью. Тогда получается, что эта единая плоскость проходит через две точки прямой СD. Тогда, по аксиоме 4, вся прямая СD принадлежит этой плос-ти, в том числе и сами точки С и D. Но плос-ть проходит также через А и В. То есть получится, что А, В, С и D входят в состав одной плос-ти, а это не так. Это противоречие означает, что на самом деле все плоскости, проходящие через разные точки прямой CD, будут различны, ч. т. д.

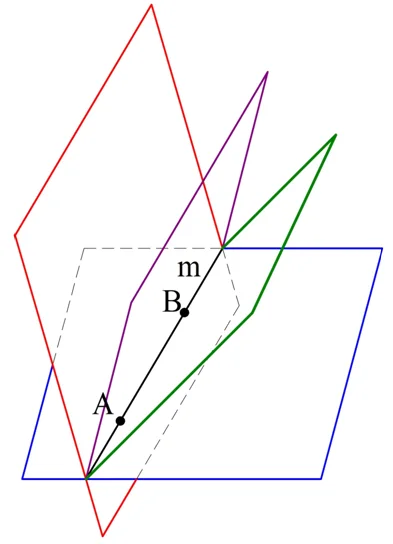
Рассмотрим ещё одну теорему:

Пусть пересекаются прямые m и n. Обозначим точку их пересечения как А. Также выберем на m некоторую точку В, а на n – точку C. Мы можем построить плос-ть α через точки А, В и C, и она будет единственной. Так как и А, и В принадлежат α, то и вся прямая m ей принадлежит (аксиома 4). Аналогично и прямая n находится на плос-ти α. То есть α как раз и является плос-тью, о которой говорится в теореме. Никакая другая плос-ть не будет содержать обе прямые m и n, ведь в противном случае она проходила бы через точки А, В и С, то есть совпадала бы с α.

Эта теорема также говорит о том, что две пересекающиеся прямые однозначно определяют проходящую через них плос-ть.

Что такое стереометрия

Определение

Стереометрия — раздел евклидовой геометрии, в котором изучаются свойства фигур в пространстве.

Если основными фигурами планиметрии являются точка и прямая, то в стереометрии к изучению добавляется плоскость.

Примеры стереометрических фигур:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

• шар;
• сфера;
• конус;
• цилиндр;
• призма и так далее.

Нередко основным способом решения задач в стереометрии является рассмотрение разнообразных плоскостей при выполнении планиметрических законов.

В стереометрии используются следующие обозначения: 

• прописные буквы A,B,C,D обозначают точки;
• строчные буквы обозначают прямые, например, AB = a; 
• плоскости, как правило, обозначаются такими буквами как \(\alpha,\;\beta,\;\gamma\) и подобными;
• принадлежность точек к прямой или точек и прямых к плоскости обозначается стандартно: \(A\;\in\;a\) или \(b\;\in\;\alpha.\)

Зачем нужны аксиомы

Математику изучают в школе не просто так. Большинство забудет все эти уравнения, графики и аксиомы сразу после ЕГЭ в 11 классе.

Задача школьного курса математики состоит в том, чтобы вы освоили научное мышление. Чтобы поняли, как работает наука, как проверяются гипотезы и как доказываются утверждения. И чем отличается частный жизненный опыт от универсальных знаний.

Подробнее о том, чем научное знание отличается от обывательского (и почему это так важно), смотрите в цикле уроков «Как работает наука». Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств

Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих

Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств. Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих.

Простой пример «очевидного» утверждения. Биссектриса треугольника пересекает его противоположную сторону:

Спасибо, Капитан Очевидность. Однако напрямую этот факт ниоткуда не следует. Его можно доказать, например, через тригонометрию или координаты. Но потребовать такое доказательство — отличная задача-гроб на устном экзамене в университет.

Создание системы аксиом — долгий и кропотливый процесс. Классическая евклидова геометрия, которую изучают в школе, основана на аксиомах, которые формировались более двух тысяч лет. Основоположник этих аксиом — Евклид — жил в III веке до н.д. Собственно, потому геометрия и называется евклидовой.

Зато когда система аксиом построена, все последующие теоремы выводятся из неё через логические рассуждения. Без привлечения наглядных иллюстраций и «очевидных соображений». Вот здесь и начинается настоящая наука.:)

Углы между прямой и плоскостью

Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?

И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. 

Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой. 

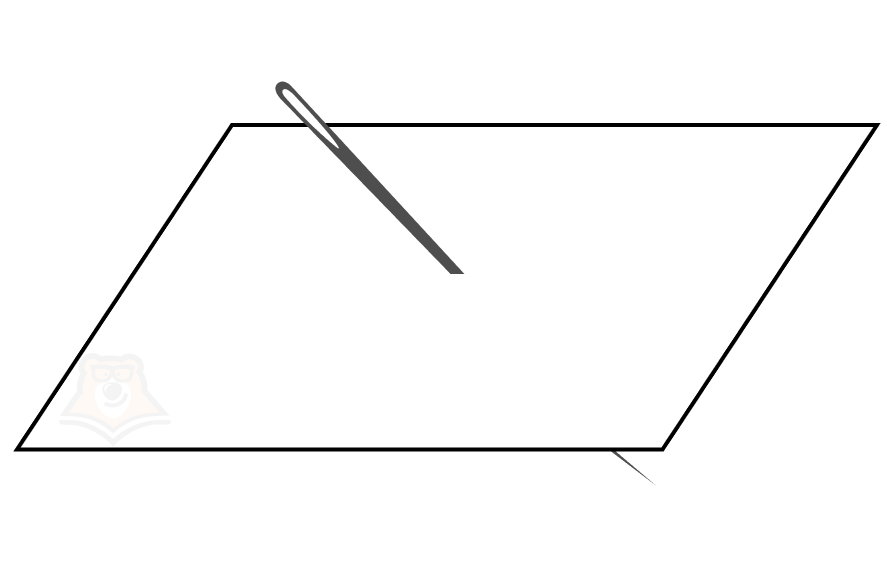
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О. 

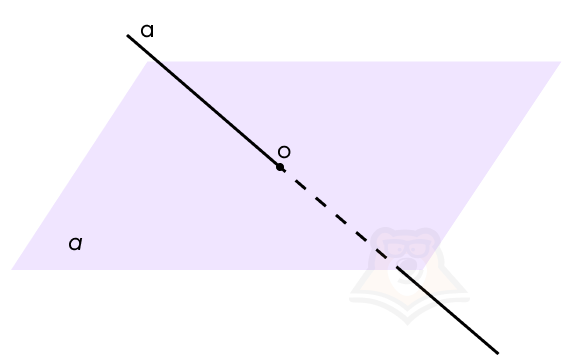
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость. 

Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А₁. 

Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость. 

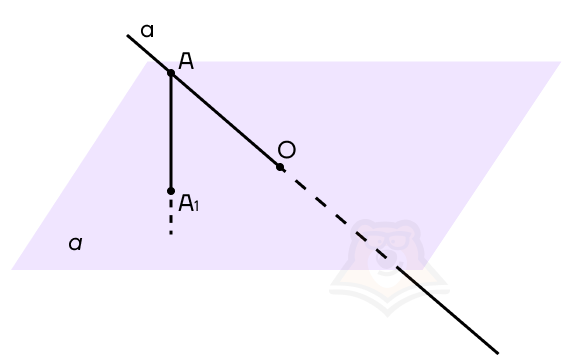
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А₁ и О, получаем, что А₁О — проекция прямой а на плоскость а. 

Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А₁О. 

Проекция прямой а на плоскость — это прямая а₁, образованная проекциями всех точек прямой а на плоскость. 

Таким образом можно построить проекции не только прямой, но и любой фигуры.

Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А₁ОА. 

В этом случае мы также берем острый угол, образованный прямой и плоскостью. 

Алгоритм нахождения угла между прямой и плоскостьюШаг 1. Построить проекцию прямой на плоскость.Шаг 2. Найти угол между прямой и построенной проекцией.

Если прямая параллельна плоскости угол будет равен 0. 

Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.  

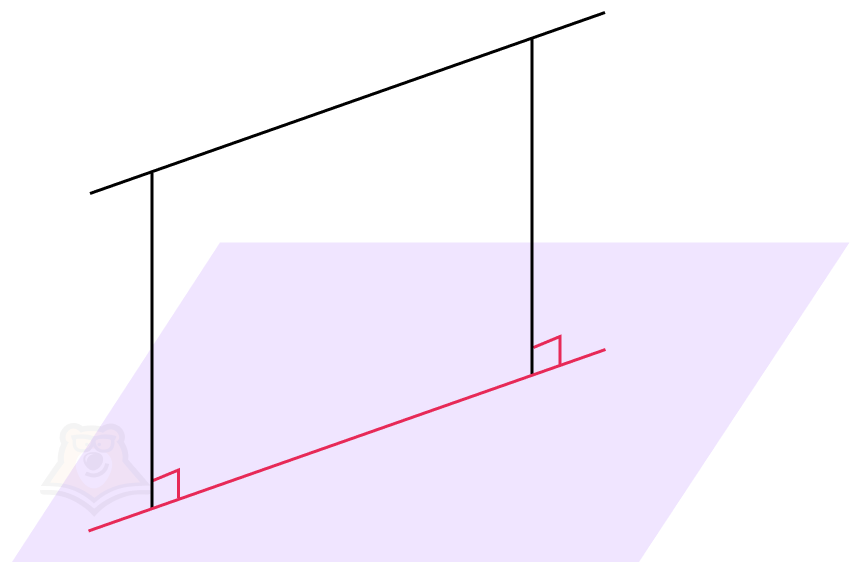
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.

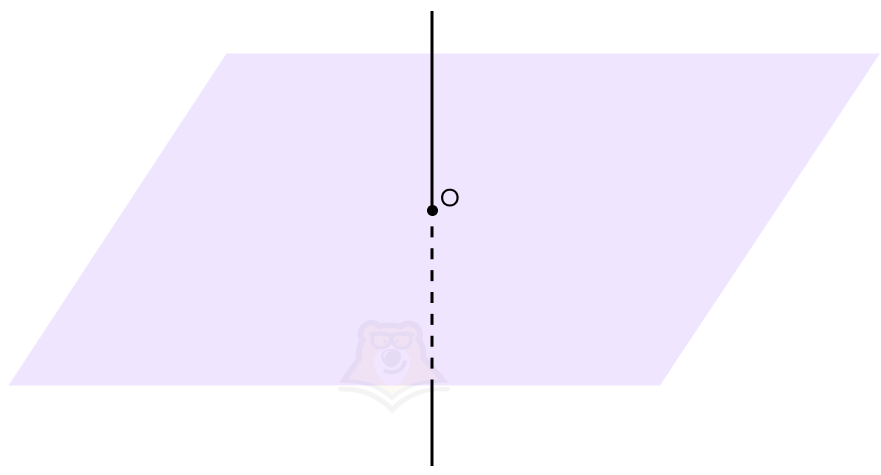
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости. 

Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. 

А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?

Для этого существует признак перпендикулярности прямой и плоскости:

Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости. 

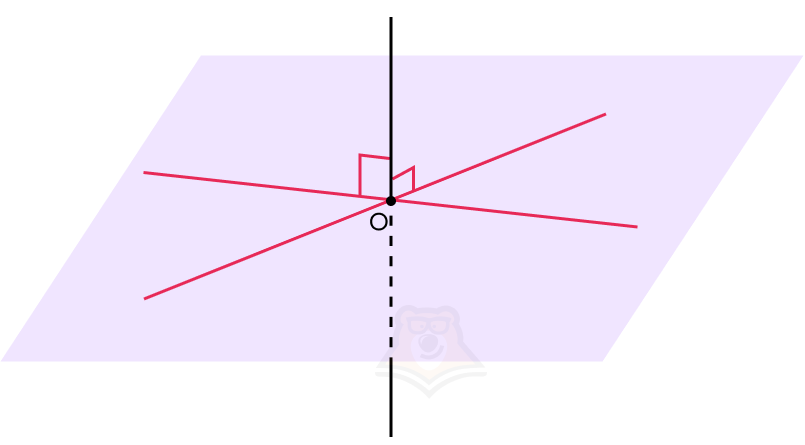
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.

Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости. 

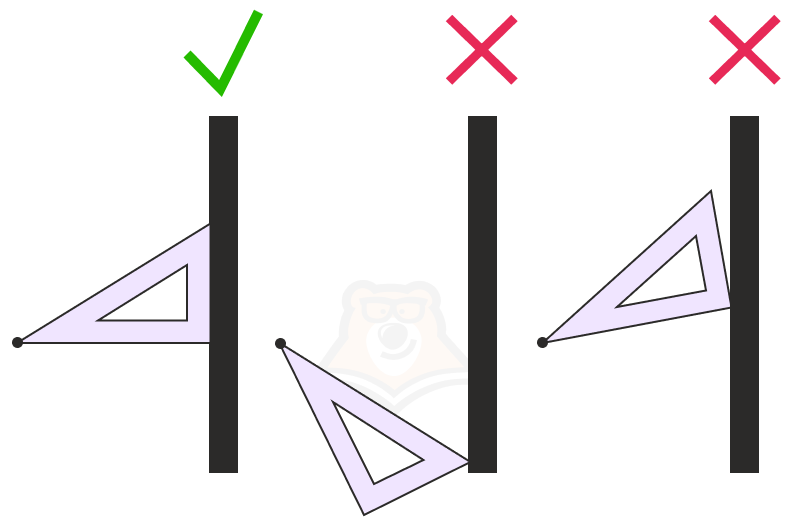
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости. 

Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет. 

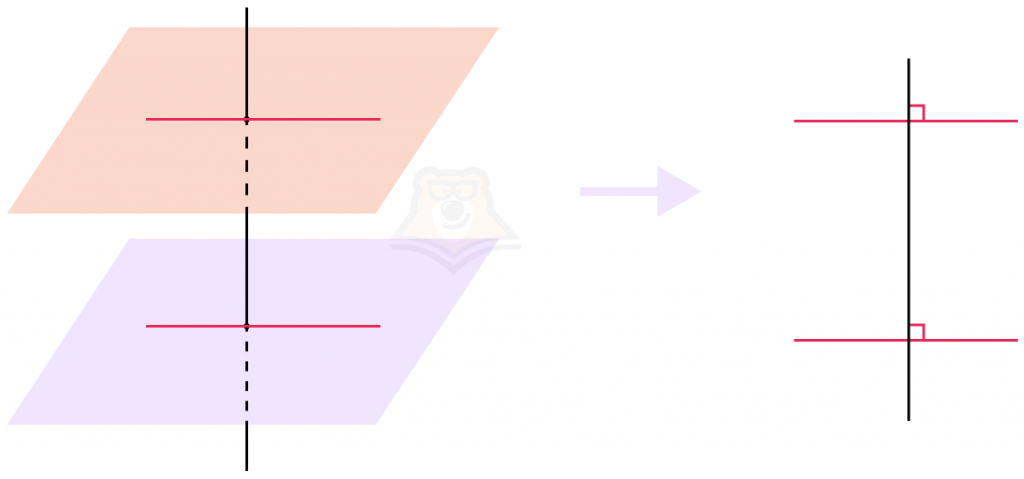
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны. 

Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны. 

Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”. 

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны. 

Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”. 

Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны. 

Это легко проверить, если найти любой двугранный угол между построенными плоскостями. 

Стереометрия

Стереометрия
(от др.-греч. στερεός, «стереос» — «твёрдый, объёмный, пространственный» и μετρέω, «метрео» — «измеряю») — раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки, прямые и плоскости. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путём рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Аксиомы стереометрии

• На каждой прямой и в каждой плоскости имеются по крайней мере две точки.
• В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
• Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
• Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
• Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
• Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
• Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
  1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
  2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
• Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми. Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань.

Литература

• В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
• И. Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Выпуск 31).

Анализ Классический анализ Теория функций Дифференциальные и
интегральные уравнения

Геометрия и топология Геометрия Топология

Дискретная математика

• Портал «Математика»
• Категория «Математика»

Аксиомы стереометрии и следствия из них

Упростить решение множества задач и изучение стереометрии позволяет знание основных положений и правил. К примеру, существуют аксиомы, которые не нуждаются в доказательстве. С их помощью достаточно просто выполнять построение классических и сложных фигур, производить разнообразные вычисления. Перечислим их.

Аксиома 1: Если 3 точки не принадлежат общей прямой, то через них допустимо построить плоскость в единственном экземпляре.

Аксиома 2: При нахождении 2 точек какой-то прямой в некой плоскости можно сделать вывод о расположении в этой же плоскости остальных точек рассматриваемой прямой.

Аксиома 3: В том случае, когда пара плоскостей обладает общей точкой, можно сделать вывод о наличии у таких плоскостей одной прямой, содержащей каждую из точек пересечения рассматриваемых плоскостей.

Аксиома 4: В какой-либо пространственной плоскости справедлива каждая из аксиом планиметрии.

При анализе перечисленных аксиом можно сформулировать некоторые закономерности. Такие утверждения называют следствиями. Перечислим их.

Следствие 1

Если имеется какая-то прямая и точка, ей не принадлежащая, то через данные элементы допустимо провести единственную плоскость.

Следствие 2

Если 2 прямые линии пересекаются между собой, то с их помощью допустимо построить единственную плоскость.

Следствие 3

В том случае, когда имеется пара прямых, расположенных параллельно относительно друг друга, через них допустимо провести единственную плоскость.

Следствие 4

Когда прямая не расположена на некоторой плоскости, данные элементы обладают максимум одной единой точкой.

Аксиомы стереометрии

В стереометрии справедливы все аксиомы планиметрии, а именно:

1. все точки или принадлежат данной прямой, или не принадлежат ей;
2. через любые $2$-е точки можно провести $1$-ну прямую;
3. только одна из $3$-х точек на прямой может лежать между $2$-мя другими;
4. длина любого отрезка прямой отлична от нуля;
5. длина отрезка складывается из длин частей, на которые он делится любой его точкой;
6. любой угол имеет определенную меру, отличную от нуля;
7. мера угла складывается из мер углов, на которые он делится любым лучем, проходящим между его сторонами;
8. аксиома Эвклида — через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

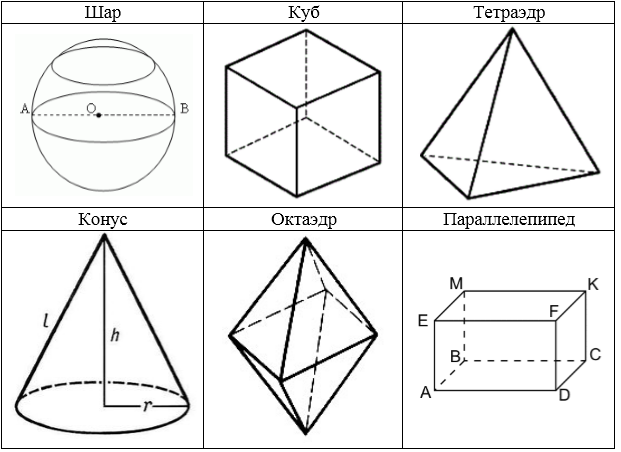
Предмет стереометрии

Определение

Стереометрия — раздел геометрии, изучающий свойства пространственных фигур.

К основным из них относятся — точка, прямая и плоскость. Точка и прямая известны из планиметрии.

Например, поверхность стола дает представление о части плоскости.

В геометрии считают, что плоскость ровная и неограниченная, не имеет краев и толщины.

На рисунках часть плоскости чаще всего изображают в виде произвольной замкнутой фигуры и обозначают буквами греческого алфавита $\alpha ,\; \beta ,\; \gamma ,\; \ldots $ и т.д.

Примеры других популярных фигур стереометрии:

Аксиомы стереометрии

В стереометрии справедливы все аксиомы планиметрии, а именно:

1. все точки или принадлежат данной прямой, или не принадлежат ей;
2. через любые $2$-е точки можно провести $1$-ну прямую;
3. только одна из $3$-х точек на прямой может лежать между $2$-мя другими;
4. длина любого отрезка прямой отлична от нуля;
5. длина отрезка складывается из длин частей, на которые он делится любой его точкой;
6. любой угол имеет определенную меру, отличную от нуля;
7. мера угла складывается из мер углов, на которые он делится любым лучем, проходящим между его сторонами;
8. аксиома Эвклида — через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Дополнительные аксиомы стереометрии

Статья: Стереометрия

Найди решение своей задачи среди 1 000 000 ответов

Аксиома 1

Все точки или принадлежат данной плоскости, или не принадлежат ей. На рисунке точки $A$ и $B$ принадлежат плоскости $\alpha $ (плоскость $\alpha $ проходит через эти точки), а точки $C$ и $D$ — не принадлежат.

Аксиома 2

Все точки прямой принадлежат плоскости, если этой плоскости принадлежат любые $2$-е её точки. На рисунке точки $A$ и $B$ прямой $s$ принадлежат плоскости $\alpha $, поэтому и прямая $s$, которой принадлежат эти точки, также принадлежат плоскости $\alpha $.

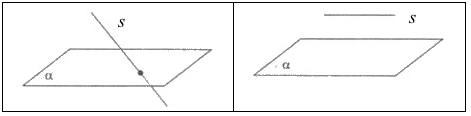
На рисунках ниже представлены два случая, когда прямая $s$ не принадлежит плоскости.

Аксиома 3

Две плоскости пересекаются по прямой, которая проходит через общую точку этих плоскостей.

На рисунке плоскости $\alpha $ и $\beta $ имеют общую точку R, то есть точка R принадлежит как плоскости $\alpha $, так и плоскости $\beta $. Точка R принадлежит также прямой $s$. Значит, плоскости $\alpha $ и $\beta $ пересекаются по прямой $s$.

Аксиома 4

Через любые три точки, не лежащие на одной прямой, можно провести единственную плоскость. Иначе говоря, любые три точки в пространстве всегда лежат в одной плоскости.

На рисунке точки M, N и K не лежат на $1$-ной прямой. Поэтому существует единственная плоскость $\alpha $, которой принадлежат все эти точки.

Следствия из аксиом стереометрии.

Следствие 1

Через прямую $s$ и точку T, не лежащую на ней, можно провести $1$-ну плоскость $\alpha $.

Следствие 2

Через $2$-е пересекающиеся прямые p и q можно провести $1$-ну плоскость $\alpha $.

Следствие 3

Плоскость можно задать а) $3$-мя точками, не лежащими на $1$-ной прямой, б) прямой и точкой, не лежащей на ней, в) $2$-мя пересекающимися прямыми, г) $2$-мя параллельными прямыми.

Следствие 4

Возможны три случая взаимного расположения прямых в пространстве:

1. пересекающиеся прямые лежат в $1$-ной плоскости и имеют общую точку;

параллельные прямые лежат в $1$-ной плоскости и не имеют общих точек;

скрещивающиеся прямые AB и CD — не лежащие в $1$-ной плоскости.

Аксиомы стереометрии с рисунками

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.

Следствие 4. Из аксиомы (математическое утверждение не требующее доказательства) 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

1. Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.

2. Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

3. Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

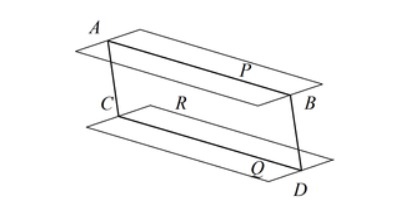
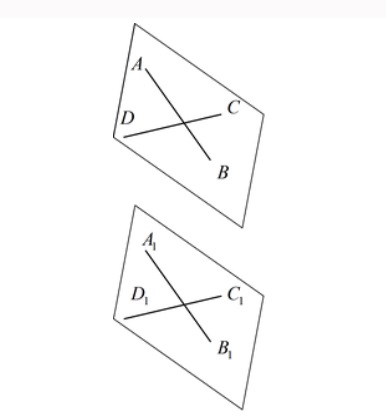
4. Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A₁B₁ и C₁D₁ другой плоскости, то эти плоскости параллельны.

Теоремы о перпендикулярности прямых и плоскостей

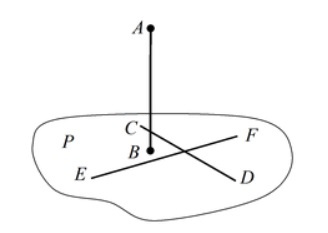
1. Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.

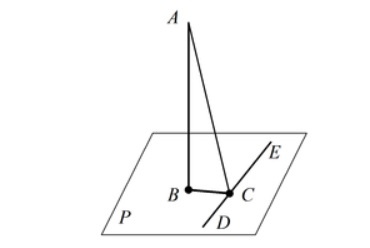
2. Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).

3. Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.

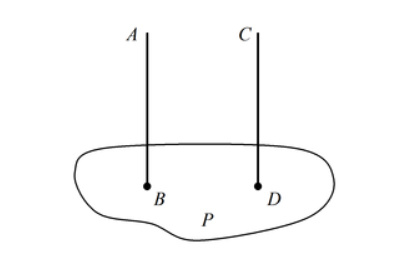
4. Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.

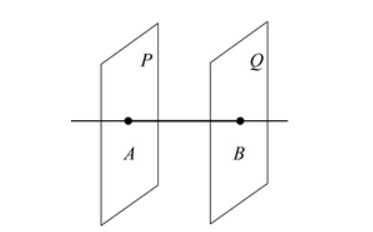
Теоремы о перпендикулярности плоскостей

1. Если плоскость P проходит через перпендикуляр к другой плоскости Q, то плоскость P перпендикулярна плоскости Q.

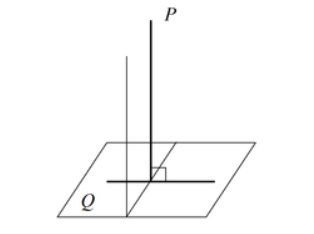
2. Если две плоскости P и Q взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.

Теорема о скрещивающихся прямых

1. Угол \(\alpha\) между скрещивающимися прямыми AB и CD определяется как угол между одной из этих прямых (например, CD) и любой прямой A₁B₁, проходящей через ее произвольную точку E параллельно другой прямой.

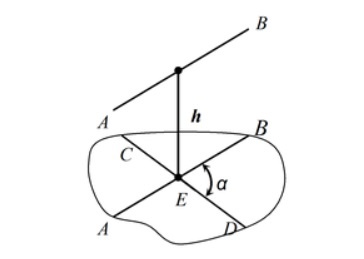
2. Расстояние h между скрещивающимися прямыми AB и CD определяется как кратчайшее расстояние от одной из этих прямых и может быть найдено как расстояние от одной их этих прямых (например, AB) до плоскости P, проходящей через другую прямую CD параллельно первой.

Решение задач

Аксиомы стереометрии часто применяются в доказательствах. И ещё в задачах с открытыми вопросами. Вот пример такой задачи:

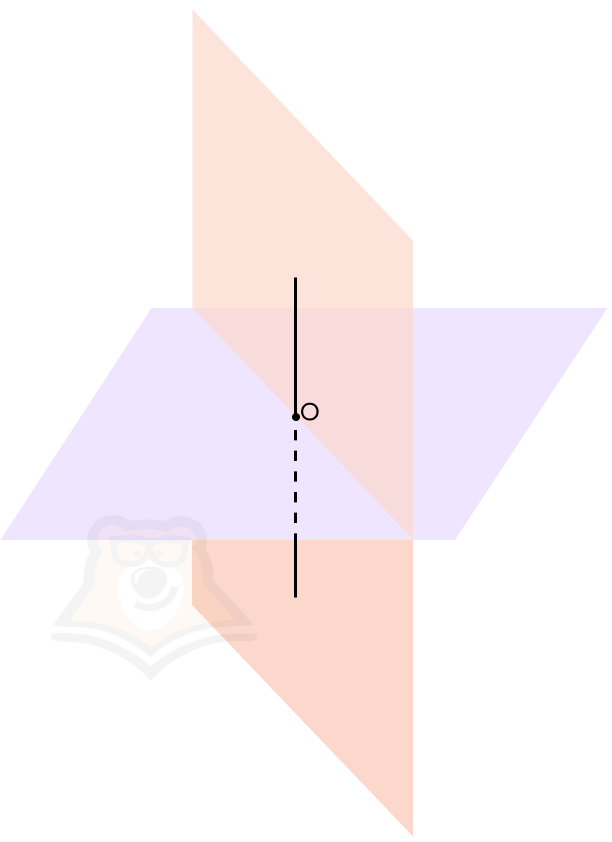
Задача 1. Окружность и плоскость

Решение. Легко заметить, что ответ зависит от взаимного расположения точек $M$, $N$ и $O$.

Допустим, что все они лежат на одной прямой. Тогда $MN$ — диаметр, и вся окружность может как лежать в плоскости $\alpha $, так и не лежать в ней. Вот пример когда окружность не лежит в плоскости:

Пусть теперь точки $M$, $N$ и $O$ не лежат на одно прямой. По Аксиоме плоскости (Аксиома 4 в нашем списке) эти точки однозначно задают плоскость. Эта плоскость совпадает с плоскостью $\alpha $.

А поскольку окружность — плоская фигура, то остальные её точки также принадлежат плоскости $\alpha $:

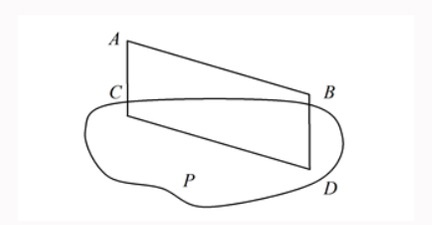
Задача 2. Неравильный рисунок

Решение. Соединим точки $M$ и $K$ прямой $l$:

Мы видим, что точка $B\notin l$. Поэтому точки $M$, $B$, $K$ не лежат на одной прямой. И согласно Аксиоме плоскости (Аксиома 4 в нашем списке), эти точки однозначно задают плоскость.

С одной стороны, мы видим по рисунку, что это плоскость $\alpha $. С другой стороны, параллелограмм — плоская фигура, поэтому точки $M$, $B$, $K$ лежат ещё и в плоскости параллелограмма. А это значит, что плоскости $\alpha $ и $ABCD$ должны совпадать, чего на рисунке не происходит.

Есть и другой способ показать, что рисунок некорректен. По условию задачи, точки $M$, $B$, $K$ являются общими для плоскости $\alpha $ и плоскости $ABCD$. Согласно Аксиоме пересечения плоскостей (Аксиома 5 в нашем списке), все эти точки должны лежать на одной прямой.

Однако простое построение показывает, что точки $M$, $B$, $K$ не лежат на одной прямой, что противоречит аксиоме. Такое противоречие как раз и доказывает некорректность чертежа.

Далее мы будем лишь называть аксиомы — без нумерации.

Задача 3. Прямые на плоскости

Решение. Нарисуем прямые $a$, $b$, $c$ и обозначим их точки пересечения $M$, $N$, $K$:

Точки $M$, $N$, $K$ не лежат на одной прямой. По основной Аксиоме плоскости, эти три точки однозначно определяют некоторую плоскость $\alpha $.

Далее заметим, например, что точки $M\in \alpha $ и $N\in \alpha $ по построению. По основной Аксиоме прямой и плоскости вся прямая $MN=b$ лежит в этой плоскости, т.е. $b\subset \alpha $.

Аналогично доказывается, что прямые $a\subset \alpha $ и $b\subset \alpha $.

Задача 4. Пересечение плоскостей

Решение. Обозначим прямую, по которой пересекаются плоскости $\alpha $ и $\beta $, буквой $l$:

\

Дополнительное построение: прямая $AB$, которая пересекает прямую $l$ в точке $M$:

Точки $A\in \alpha $, $B\in \alpha $. По основной Аксиоме прямой и плоскости прямая $AB\subset \alpha $ — искомая линия сечения плоскости $\alpha $ и $ABC$.

Далее заметим, что точка $M\in l\subset \beta $. Дополнительное построение: прямая $CM$:

Точки $C\subset \beta $, $M\subset \beta $. И вновь по основной Аксиоме прямой и плоскости прямая $CM$ — искомая линия сечения плоскости $\beta $ и $ABC$.

Хочу отметить, что задачи на построение — это отдельный класс задач. Как в планиметрии, так и в стереометрии. Там много интересных моментов, им посвящены отдельные уроки. А то, что мы сделали сейчас — это совсем уж простые рассуждения, которые тем не менее опираются на всю мощь аксиом.

Задача 5. Стандартное доказательство

Решение. Это классическая задача на доказательство, которую в разных формулировках предлагают во всех учебниках по стереометрии.

Обозначим параллелограмм $ABCD$. Пусть $O$ — точка пересечения диагоналей.

Поскольку точка $O\notin AB$, точки $A$, $B$, $O$ не лежат на одной прямой. По основной Аксиоме плоскости эти три точки однозначно определяют плоскость. Обозначим эту плоскость $\alpha $.

Точки $A\in \alpha $, $O\in \alpha $. По основной Аксиоме прямой и плоскости, прямая $AO\subset \alpha $. Но точка $C\in AO\subset \alpha $. Следовательно, вершина параллелограмма $C\in \alpha $. Аналогично через точки $B$ и $O$ доказывается, что вершина $D\in \alpha $.

Замечание по поводу задач

Как видите, мы рассмотрели лишь самые простые задачи

Но даже на их примере видно, насколько важно чётко знать систему аксиом

Бесчисленное множество контрольных и экзаменов были завалены просто потому, что ученик не смог обосновать простые и наглядные рассуждения. Потому что, например, не знал: можно ли утверждать, что если две точки прямой лежат на плоскости, то и вся прямая лежит на этой плоскости.

В общем, учите аксиомы и практикуйтесь на простых примерах. А для более интересных задач нам потребуются некоторые следствия из этих аксиом. Чему и посвящён следующий урок.:)

1. Следствия из аксиом стереометрии
2. Теорема о трёх перпендикулярах
3. Комментарий к пробному ЕГЭ от 7 декабря
4. Метод Гаусса
5. Задачи про температуру и энергию звезд
6. Задача B4 про шерсть и свитер

Проверь себя

Задание 1. Выберите верное утверждение. 

1. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
2. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
3. Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
4. Ребра двугранного угла — это плоскости, которые его образуют. 

Задание 2. Угол между плоскостями — это…

1. Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
2. Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
3. Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
4. Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3. Что такое проекция прямой на плоскость?

1. Это любая прямая, проведенная из точки пересечения прямой и плоскости;
2. Это перпендикуляр, опущенный из любой точки на плоскость;
3. Это всегда точка пересечения прямой и плоскости;
4. Это прямая, образованная проекциями всех точек прямой на плоскость. 

Задание 4. Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?

1. Проекция будет равна этой прямой и параллельна ей;
2. Проекция будет меньше прямой и образовывать с ней угол;
3. Проекция будет точкой пересечения прямой и плоскости;
4. Проекция будет больше прямой и образовывать с ней угол.  

Задание 5. Как доказать, что прямая перпендикулярна плоскости?

1. Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
2. Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
3. Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
4. Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4