Медианы, биссектрисы, высоты треугольника

Третий признак равенства треугольников

Доказательство. Даны два треугольника $\bigtriangleup{ABC}$ и $\bigtriangleup{A_{1}B_{1}C_1}$, в которых $AB=A_{1}B_1,~BC=B_{1}C_1$ и $CA=C_{1}A_1$. Наложим треугольники друг на друга так, чтобы вершина $C_1$ располагалась в одной полуплоскости с вершиной $C$. Поскольку $AB=A_{1}B_1,$ точка $A$ совпадет с точкой $A_1,$ точка $B$ совпадет с точкой $B_1$.

Воспользуемся методом доказательства от противного и предположим, что при наложении точка $C_1$ не лежит ни на луче $BC$, ни на луче $AC$. Тогда между вершинами $C$ и $C_1$ имеется расстояние $CC_1$. Обозначим точку $D$ как середину этого отрезка.

Рассмотрим треугольники $\bigtriangleup{AC_{1}C}$ и $\bigtriangleup{BC_{1}C}$.

Они являются равнобедренными, с общим основанием $CC_1$. В них $AD$ и $BD$ — медианы, поскольку $D$ мы обозначали как середину $CC_1$.

По теореме о медиане равнобедренного треугольника, медианы $AD$ и $BD$ также будут являться высотами соответствующих треугольников. Согласно теореме о единственности перпендикуляра, к точке прямой можно провести только один перпендикуляр. У нас — два перпендикуляра $AD$ и $BD$, к одной точке $D$.

Мы пришли к противоречию. Значит, точка $C_1$ располагается либо на луче $AC$, либо на луче $BC$. Если $C_1\in{AC},$ тогда $C_1$ совпадает с точкой $C$, поскольку $CA=C_{1}A_1$. Точно так же приходим к выводу о совпадении точек $C$ и $C_1,$ если $C_1\in{BC}$. Все три точки совпадают. Треугольники равны.

Теорема доказана.

{"questions":[{"content":"`image-1` Перед вами — различные пары треугольников. Определите на чертеже, где какой признак равенства. `matcher-5`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-2-1.svg"},"matcher-5":{"type":"matcher","labels":,"items":}}}]}

Свойства биссектрисы треугольника

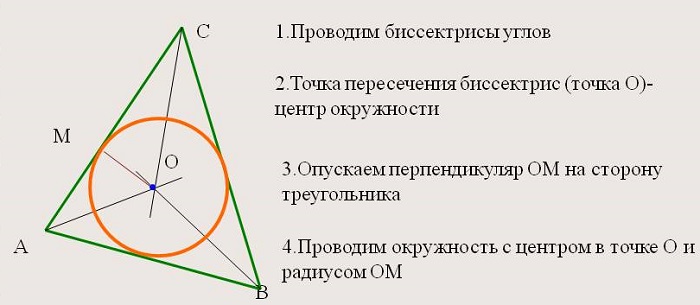
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон. 

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

S = p∗r

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5

Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6

У правильного треугольника все внешние биссектрисы параллельны сторонам;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

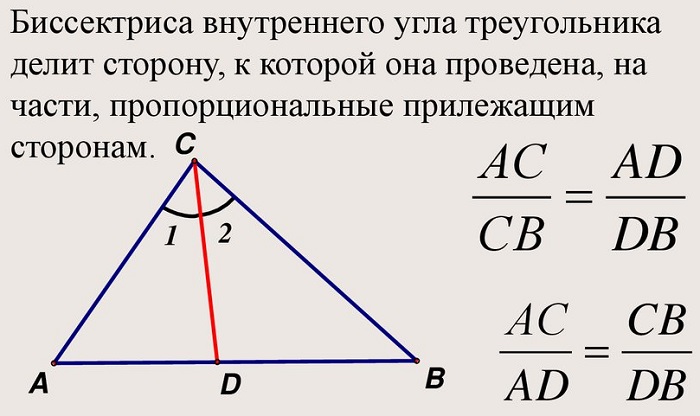
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Высота треугольника

Пусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$, образующий при этом перпендикуляр к стороне $AB$. Тогда отрезок $CD$ будет являться высотой треугольника $\bigtriangleup{ABC}$. Аналогичный перпендикуляр можно опустить как из вершины $A$, так и из вершины $B$.

Получается, что:

В остроугольном треугольнике — где углы имеют значение $<90^{\circ}$ — чертеж высот не вызывает сложности: они всегда будут пересекаться внутри треугольника. Однако если треугольник тупоугольный — один из углов имеет значение $>90^{\circ},$ — провести высоту будет уже не так интуитивно просто.

Осмотрите треугольник $\bigtriangleup{PMK}$ выше, с тупым углом $\angle{M}$.

Нам необходимо провести высоту из вершины $K$ к стороне $PM$. Подумайте, как будет располагаться отрезок, выполните чертеж и сравните свои предположения со скрытым чертежом.

Пересечение высот: как найти высоту треугольника

Выходит, что в остроугольном треугольнике высоты пересекаются в точке, расположенной строго внутри треугольника — никаких дополнительных построений не требуется.

Высоты в тупоугольном треугольнике пересекаются в точке, расположенной вне треугольника, — чтобы найти высоту треугольника, необходимо достраивать продолжение сторон

Так, в случае с нашим тупоугольным треугольником, высоты пересекаются в точке $O$ — внимание на чертеж выше

{"questions":[{"content":"`image-1` Помимо остроугольного и тупоугольного треугольника, существует треугольник прямоугольный — частный случай, когда один из углов прямой, то есть равняется $90^{\\circ}$. Что это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике?  `choice-11`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":,"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":}}}]}

Виды треугольников

Треугольник называется равнобедренным,
если у него две сторны равны. Эти равные стороны называются боковыми
сторонами, а третья сторона называется основанием треугольника.

Треугольник, у которого все сторны равны, называется равносторонним
или правильным.

Треугольник
называется прямоугольным, если у него есть прямой угол, то есть
угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому
углу, называется гипотенузой, две другие стороны называются катетами.

Треугольник называется остроугольным,
если все три его угла — острые, то есть меньше 90°.

Треугольник называется тупоугольным, если один из его углов —
тупой, то есть больше 90°.

Пример задач

Пример 1

Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то $AB=BC$.

Доказательство

Изобразим рисунок по условию задачи (рис. 5).

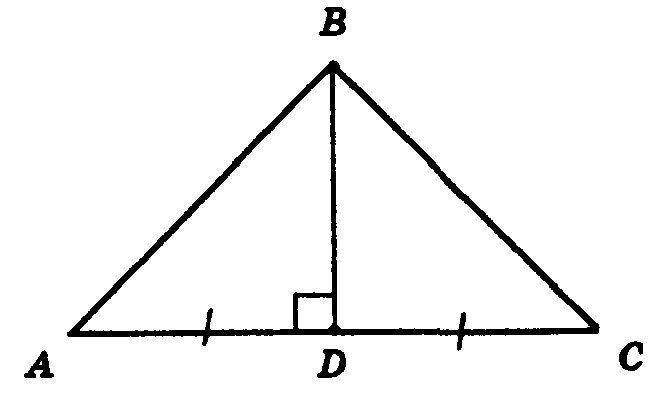
Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$

Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$

У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.

Пример 2

Пусть нам даны равные треугольники $ABC$ и $A’B’C’$. В них проведены высоты $BH$ и $B’H’$, соответственно. Доказать, что эти высоты в треугольниках будут равны между собой.

Доказательство.

Изобразим рисунок по условию задачи (рис. 6).

Так как данные треугольники равны, то будет верно равенство
$∠A=∠A’$

Так как $BH$ и $B’H’$ являются высотами, то по определению 6 будет верно равенство
$∠AHB=∠A’H’B’=90^0$

Из треугольника $ABC$, имеем

$∠ABH=180^0-90^0-∠A=90^0-∠A$

Из треугольника $A’B’C’$ и равенства углов $∠A$ и $∠A’$, получим

$∠A’B’H’=180^0-90^0-∠A’=90^0-∠A’=90^0-∠A=∠ABH$

По всему сказанному выше, треугольники $AHB$ и $A’B’H’$ равняются по первому признаку. Но тогда и стороны $BH$ и $B’H’$ равны.

Равенство треугольников

Теорема 19. Два треугольника равны, если три стороны одного соответственно равны трем сторонам другого.

Дано. В двух треугольниках ABC и DEF (черт. 43) стороны равны

AB = DE, BC = EF, AC = DF

Требуется доказать, что ∆ABC = ∆DEF.

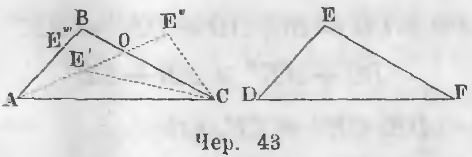
Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC точкой D на точку A. По равенству сторон AC и DF точка F упадет на точку C.

Чтобы доказать, что точка E упадет на точку B докажем, что она не может упасть ни внутри, ни вне, ни на одну из сторон треугольника.

a) Положим, что точка E упадет внутри треугольника в точку E’, тогда треугольник DEF примет положение треугольника AE’C, DE займет положение линии AE’ и EF положение линии E’C, следовательно,

AE’ = DE, E’C = EF.

Линия ABC, будучи внешней ломаной, больше линии AE’C внутренней ломаной, следовательно,

AB + BC > AE’ + E’C

Заменяя AE’ и E’C равными им сторонами DE и EF, имеем:

AB + BC > DE + EF,

но AB = DE, следовательно, BC > EF, что противоречит данным условиям. Итак, точка E не может упасть внутри треугольника.

b) Положим, точка E упала вне треугольника в точку E». В этом случае ∆AE»C = ∆DEF и тогда

AE» = DE, CE» = EF

Обозначим букой O точку пересечения линий AE» и BC. Из чертежа видно, что

AO + BO > AB
CO + OE» > E»C

Сложив эти неравенства, имеем:

AO + BO + CO + OE» > AB + E»C

Так как BO + CO = BC, AO + OE» = AE», то

BC + AE» > AB + CE»

Здесь AE» = DE, CE» = EF, следовательно,

BC + DE > AB + EF

но AB = DE.

Вычтя по равной величине из обоих частей последнего неравенства, получаем:

BC > EF

что противоречит данным условиям. Итак, точка E не может упасть вне треугольника.

c) Точка E не может упасть на одну из сторон треугольника в точку E»’, ибо стороны DC и AB равны. Точно также если бы E упала в точку O, то выходило бы, что BC > OC, но OC = EF, следовательно, BC > EF, что противоречит условию.

Итак, точка E должна непременно упасть в точку B, следовательно, при наложении сторона DE совпадет со стороной AB, а сторона EF со стороной BC и треугольник DEF с треугольником ABC.

Из равенства треугольников следует, что все остальные части их равны, т. е.

∠A = ∠D, ∠B = ∠E, ∠C = ∠F.

Теорема 20. Два треугольника равны, когда они имеют по равному углу, содержащемуся между равными сторонами.

Дано. В двух треугольниках ABC и DEF (черт. 44)

AB = DE, AD = DF, ∠BAC = ∠EDF

Требуется доказать, что ∆ABC = ∆DEF.

Примечание. Иногда указывают равные части на чертеже, отмечая их одинаковыми значками.

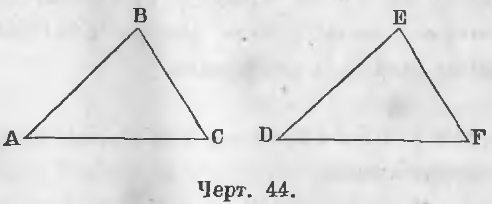
Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC, точкой D на точку A; тогда по равенству линий DF и AC точка F упадет в точку C и по равенству углов A и D линия DE пойдет по линии AB; по равенству линий DE и AB точка E упадет на точку B. Если E и F две точки линии EF совпали с B и C двумя точками линии BC, то и вся линия EF совпадет с линией BC, и треугольник DEF совпадет с треугольником ABC. Отсюда следует, что и все остальные части треугольников равны, т. е.

BC = EF, ∠B = ∠E, ∠C = ∠F.

Теорема 21. Два треугольника равны, если сторона и два лежащие на ней угла одного равны стороне и двум лежащим на ней углам другого треугольника.

Дано. В треугольниках ABC и DEF (черт. 44)

∠A = ∠D, ∠C = ∠F, AC = DF

Требуется доказать, что ∆ABC = ∆DEF.

Доказательство. Наложим треугольник DEF на треугольник ABC, стороной DF на AC, точкой D на A, тогда по равенству сторон AC и DF точка F упадет на точку C. По равенству углов A и D линия DE пойдет по линии AB и по равенству углов C и F линия FE пойдет по линии CB. Так как линия FE и DE совпадут с линиями CB и AB, то и точка E непременно совпадет с точкой B, ибо две прямые линии пересекаются в одной точке, следовательно два треугольника равны (ЧТД).

Из того, что равные треугольники совмещаются при наложении всеми своими частями вытекает следствие. В равных треугольниках против равных сторон лежат равные углы и наоборот.

Соответственные части треугольников. В двух равных треугольниках равные углы и равные стороны называются соответственными углами и сторонами.

Алгоритм доказательства равенства фигур

• Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
• На рисунке отметить, все необходимые данные в условии задания.
• Проверить есть ли у двух треугольников общая сторона либо угол.
• Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
• При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
• При необходимости, можно сделать дополнительное построение.

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Свойства

Построение биссектрисы

Свойства точек пересечения биссектрис

• Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
• Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
• Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
• Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами

• Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
• Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
• Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства биссектрис равнобедренного треугольника

• Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
• Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
• В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
• Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
• У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
• У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис

Точка пересечения биссектрисы со стороной треугольника называется основанием биссектрисы.

BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.

• Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.
• Теорема о биссектрисе — частный случай теоремы Штейнера.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
• Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
• Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
• Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .

Свойства осей биссектрис

• Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
• Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.

Другие свойства

• Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
• Расстояния от сторон угла до любой точки биссектрисы одинаковы.
• Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.
• Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника.

Равнобедренный треугольник: что такое обратная теорема

В точных науках существует понятие обратной теоремы: когда условие исходной теоремы используется в качестве заключения, а заключение — в качестве условия. Чтобы понять, как «работают» обратные теоремы, обратимся для примера к недавно нами доказанной теореме о равнобедренном треугольнике: «В равнобедренном треугольнике углы при основании равны».

Положим, что:

— утверждение $A$ — это «равнобедренность треугольника»;— утверждение $B$ — это «равенство углов при основании».

Логическая операция, к которой мы будем обращаться далее ($\Rightarrow$), формально называется импликацией (от лат. ‘implicāre’, в переводе — «впутывать»).

Тогда с точки зрения логики мы можем сказать, что из утверждения $A$ следует утверждение $B$: если $A$, то $B$. Или на языке логики — $A\Rightarrow{B}$. В обратной теореме утверждения меняются местами — $B\Rightarrow{A}$, из $B$ следует $A$. В нашем случае читается обратная теорема так: «Если углы при основании равны, то треугольник равнобедренный».

Давайте проверим ее истинность.

Доказательство

Пусть $\bigtriangleup(ABC)$ — треугольник, в котором углы при основании $AB$ равны: $\angle{A}=\angle{B}$. Рассмотрим треугольники $\bigtriangleup{ABC}$ и $\bigtriangleup{BAC}$. Они будут равны по второму признаку равенства треугольников: $AB=BA,$ $\angle{A}=\angle{B},$ $\angle{B}=\angle{A}$.

Из данного равенства следует, что $AC=BC$. Стороны при основании равны. Тогда $\bigtriangleup{ABC}$ равнобедренный. Теорема доказана.

{"questions":,"explanations":,"answer":}}}]}

Типы треугольников

Типы треугольников
Остроугольный	Тупоугольный	Прямоугольный
Разносторонний	Равнобедренный	Равносторонний

По величине углов

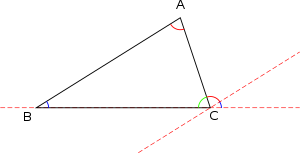
сумма углов треугольника равна 180°.

Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми(меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

• Разносторонним (неравносторонним) называется треугольник, у которого все три стороны не равны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота,медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Теорема об углах, образованных двумя параллельными прямыми и секущей

3. если две параллельные прямые пересекаются вторичной прямой, то сумма односторонних углов равна 180°. 4.

4. если точки пересечения двух прямых из точки пересечения вторичной прямой равны, то прямые параллельны.

1. Предположим, что параллельные прямые a и b пересекаются малой линией MN ( c ). Докажите, что углы пересечения 3 и 6 равны. Предположим, что углы 3 и 6 не равны. Определите угол PMN, который равен углу 6 MN, так что PMN и угол 6 являются углами пересечения MP и b MN. По построению, эти углы пересечения равны, т.е. MP || b. Предположим, что существуют две прямые (прямые a и MP ), которые проходят через точку M и параллельны прямой b. Однако это противоречит аксиоме о параллельных прямых. Следовательно, наша гипотеза неверна и угол 3 равен углу 6.

3.4 Углы с параллельными или прямыми сторонами

Если стороны угла параллельны сторонам другого угла, то эти углы равны или общие.

Немного об импликациях

Несмотря на то, что прямое и обратное следствия для равнобедренных треугольников оказались истинными, мы не можем, к примеру, сказать то же про вертикальные углы. Действительно, если углы равны… то они вертикальны? Далеко не факт. Иными словами, истинность импликации не гарантирует истинность обратной импликации.

В быту же законы логики соблюдаются редко: мы все время перемешиваем меж собой заключения и условия и, что страшнее, превращаем корреляции в импликации. Например, всем давно известная корреляция между геймингом и детской жестокостью. Нужно понимать, что корреляция — это не более чем статистическая взаимосвязь случайных величин.

Скажем, автомобилист Гриша на третьем перекрестке по дороге домой всегда попадает на зеленый свет светофора. Имеем ли мы право перейти от случайной корреляции к фактическому следствию «если $A$, то $B$»? То есть сказать: «Если Гриша едет домой, то светофор всегда будет зеленым»?

К сожалению, люди размышляют именно так. Корреляция «часто жестокие дети играют в компьютерные игры» превращается в импликацию «если дети играют в игры, то они становятся жестокими».

Или еще хуже, в обратную импликацию: «если ребенок жестокий, то он играет в компьютерные игры».

Первое дает возможность родителям безапелляционно контролировать детей. Второе — снимать какую-либо ответственность за жестокое поведение ребенка с окружения. Импликация — мощное оружие. Особенно когда она используется вне законов науки логики. Так что в следующий раз, если услышите нечто подобное, можете смело заявить о некорректном переходе от корреляции к импликации.

Элементы треугольника

Треугольник с вершинами A, B и C обозначается как  (см. рис.). Треугольник  имеет три стороны:

• сторона ;
• сторона ;
• сторона .

Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):

• ;
• ;
• .

Треугольник  имеет следующие углы:

• угол  — угол, образованный сторонами  и  и противолежащий стороне ;
• угол  — угол, образованный сторонами  и  и противолежащий стороне ;
• угол  — угол, образованный сторонами  и  и противолежащий стороне .

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).

Внешним углом плоского треугольника при данной вершине называется угол, смежный внутреннему углу треугольника при этой вершине. Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.

Архив записей

Архив записейВыберите месяц Ноябрь 2022  (1) Сентябрь 2022  (1) Январь 2022  (2) Сентябрь 2021  (1) Июль 2021  (1) Июнь 2021  (2) Май 2021  (1) Апрель 2021  (1) Март 2021  (1) Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)