Важная теория по стереометрии

Расстояние между двумя фигурами

Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.

Определение расстояния: Расстоянием между двумя точками называют длину отрезка AB.

Точка, лежащая на прямой

Расстояние равно 0.

Точка, не лежащая на прямой

Определение расстояния: Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.

Две параллельные прямые параллельные прямые

Определение расстояния: Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.

Две пересекающиеся прямые пересекающиеся прямые

Расстояние равно 0.

Определение расстояния: Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Расстояние равно 0.

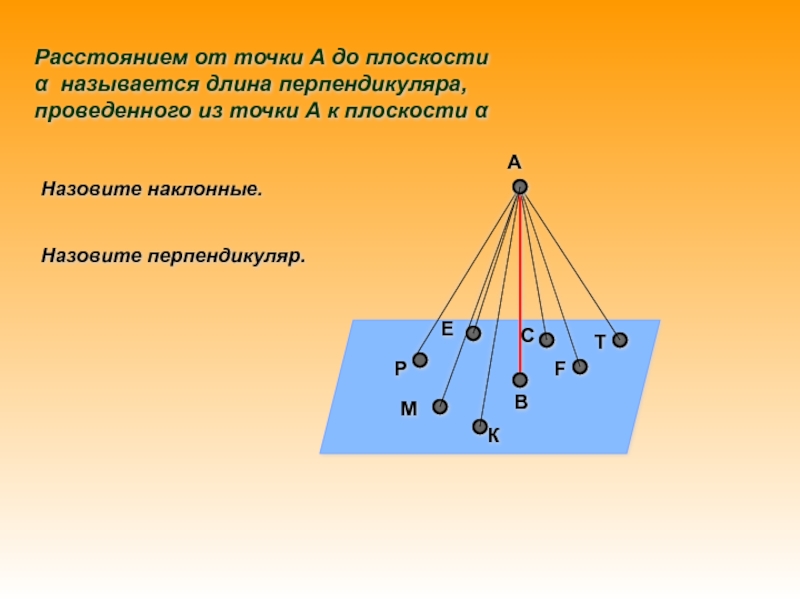
Определение расстояния: Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.

Расстояние равно 0.

Расстояние равно 0.

Определение расстояния: Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.

Расстояние равно 0.

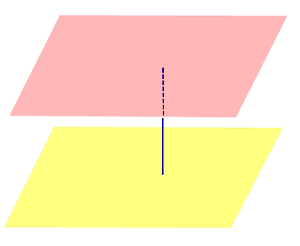
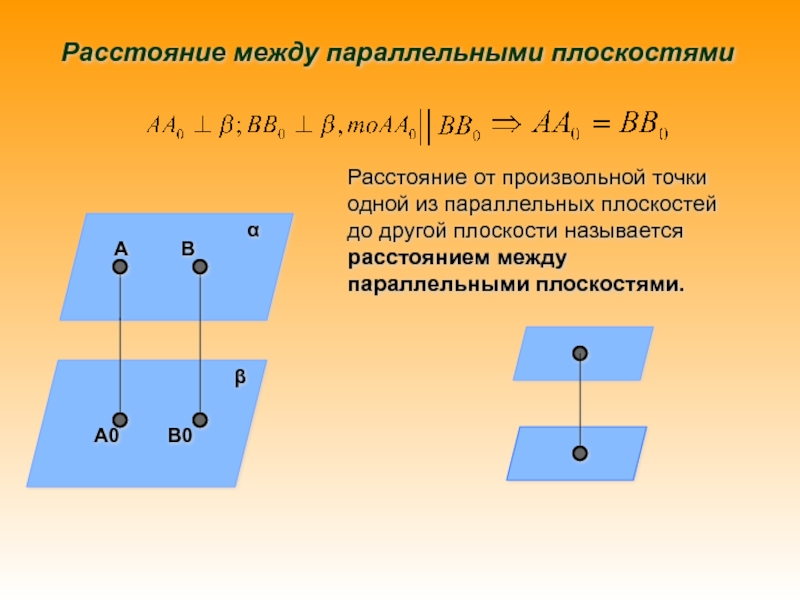
Определение расстояния: Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).

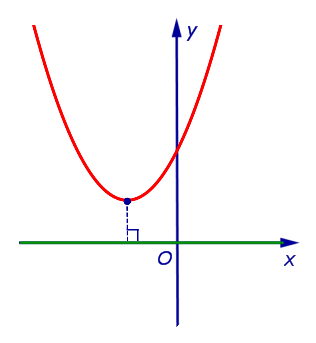
Определение расстояния: Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.

Окружность и не пересекающая ее прямая

Две непересекающиеся окружности, каждая из которых лежит вне другой Две непересекающиеся окружности, каждая из которых лежит вне другой

Метод координат для определения расстояния

Разберем пошагово способ определения расстояния между двумя скрещивающимися прямыми с помощью метода координат.

1. Определить координаты точек \(М_1\) и \(М_2\), лежащих соответственно на прямых a и b.
2. Найти x, y и z направляющих векторов для прямых a и b.
3. Найти вектор-нормаль для плоскости, в которой лежит прямая b с помощью векторного произведения \(\overrightarrow a\) и \(\overrightarrow b\).
4. Записать общее уравнение плоскости: \(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\) и потом записать к нормированному виду уравнения плоскости, которое выглядит так: \(x\times\cos\left(\alpha\right)+y\times\cos\left(\beta\right)+z\times\cos\left(\gamma\right)-p=0\), где p — свободный член (число, которое равно расстоянию точки начала координат до плоскости), а \(\cos\left(\alpha\right),\;\cos\left(\beta\right)\) и \(\cos\left(\gamma\right)\) — координаты единичного нормального вектора плоскости.
5. Далее, для определения расстояния от точки M до искомой плоскости, воспользуемся следующим уравнением: \(M_1H_1=\left|x_1\times\cos\left(\alpha\right)+y_1\times\cos\left(\beta\right)+z_1\cos\left(\gamma\right)-p\right|\), где \(x_1\), \(y_1\) и \(z_1\) — координаты точки \(M_1\), лежащей на прямой a, а \(H_1\) — точка, лежащая на искомой плоскости.

Теорема о трех перпендикулярах

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Дано:

Доказать:

Рис. 4.

Доказательство:

Пусть нам дана плоскость α (рис. 4). Проведем перпендикуляр АН к плоскости α, АМ — наклонная, М – основание наклонной. НМ – это проекция наклонной АМ на плоскость α. В плоскости α проведем прямую а через основание наклонной М перпендикулярно проекции НМ. Нужно доказать, что прямая а перпендикулярна наклонной АМ.

Прямая АН перпендикулярна плоскости α, а значит, и всем прямым, лежащим в ней. Значит, прямая АН перпендикулярна прямой а. Прямая НМ перпендикулярна прямой а по условию. Имеем, что прямая а перпендикулярна двум пересекающимся прямым АН и НМ плоскости АНМ, значит, по признаку, прямая а перпендикулярна плоскости АНМ. Прямая АМ лежит в плоскости АНМ. Значит, прямая а перпендикулярна прямой АМ, что и требовалось доказать.

Слайды и текст этой презентации

ТРЕХ ПЕРПЕНДИКУЛЯРАХПОКАЗАТЬ ПРИМЕНЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА ПРИ РЕШЕНИИ ЗАДАЧ

до н. э.).

Слайд 6Угол между прямыми равен 90°. Как называются такие прямые? -ПерпендикулярныеВерно

прямой лежащей в этой плоскости?» -ДаПродолжите предложение: «Прямая перпендикулярна плоскости, если она …»-Перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскостиЧто можно сказать о двух( 3-х, 4-х) прямых, перпендикулярных к одной плоскости? -Они параллельныКак определяется расстояние от точки до прямой на плоскости?-Как кратчайшее расстояние от точки до прямой, как длина перпендикуляра, проведенного из точки к данной прямойВспомним как называются отрезки АМ-? АН-? Точка М? Точка-Н?А как же определить расстояние от точки до плоскости?

а

А

Н

М

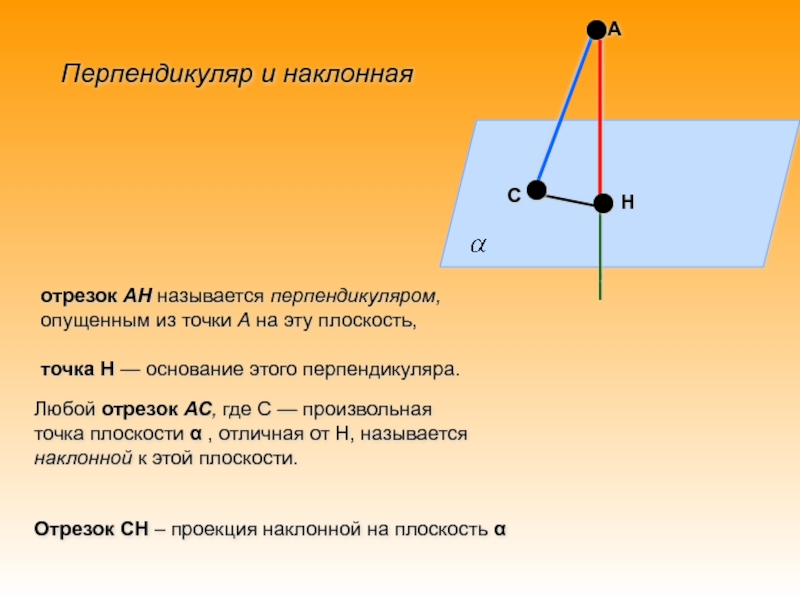
Слайд 7АНСотрезок АН называется перпендикуляром, опущенным из точки А на эту

плоскость, точка Н — основание этого перпендикуляра. Любой отрезок АС,

где С — произвольная точка плоскости α , отличная от Н, называется наклонной к этой плоскости.

Отрезок СН – проекция наклонной на плоскость α

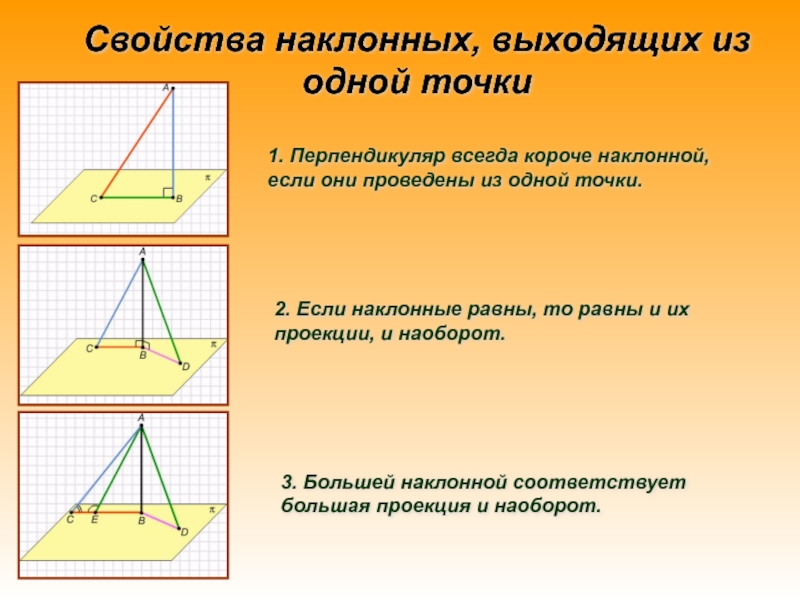
Перпендикуляр и наклонная

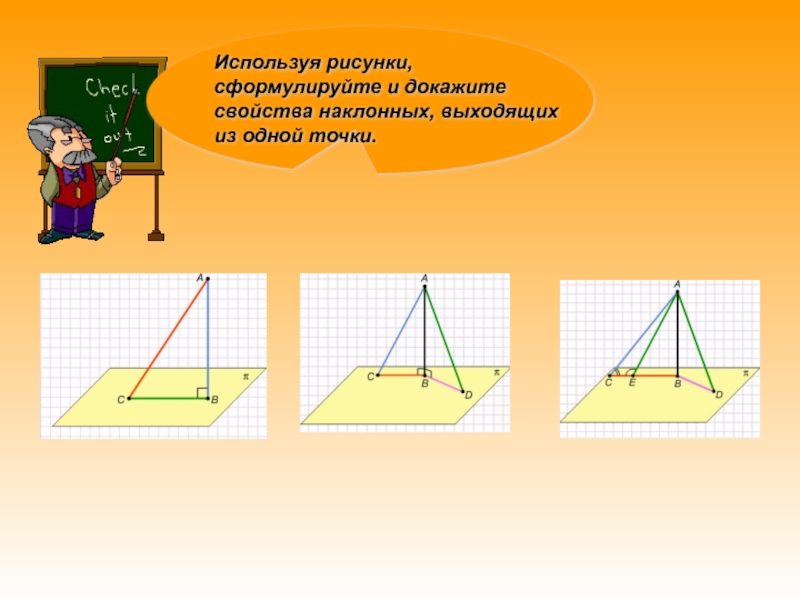
равны и их проекции, и наоборот.

3. Большей наклонной соответствует большая проекция и наоборот.

Слайд 11α β АА0 ВВ0 Расстояние между параллельными плоскостямиРасстояние от произвольной

точки одной из параллельных плоскостей до другой плоскости называется расстоянием

между параллельными плоскостями.

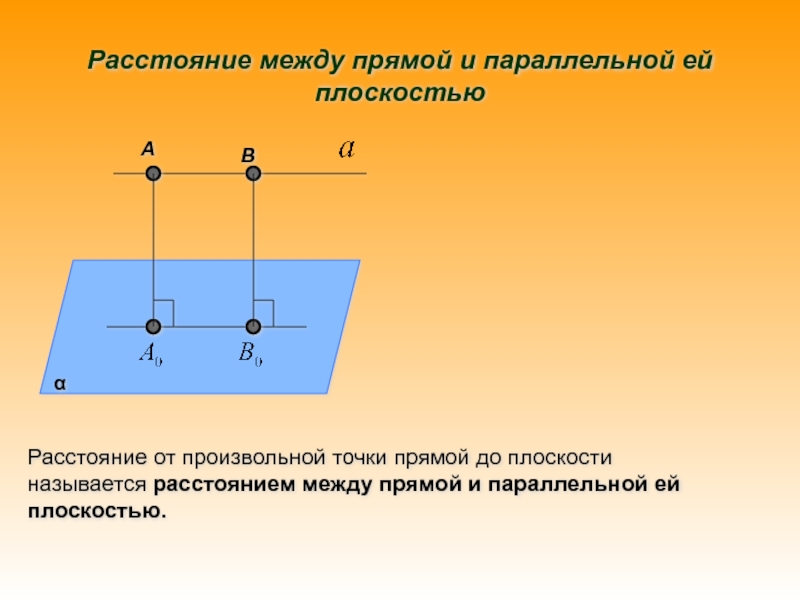
точки прямой до плоскости называется расстоянием между прямой и параллельной

ей плоскостью.

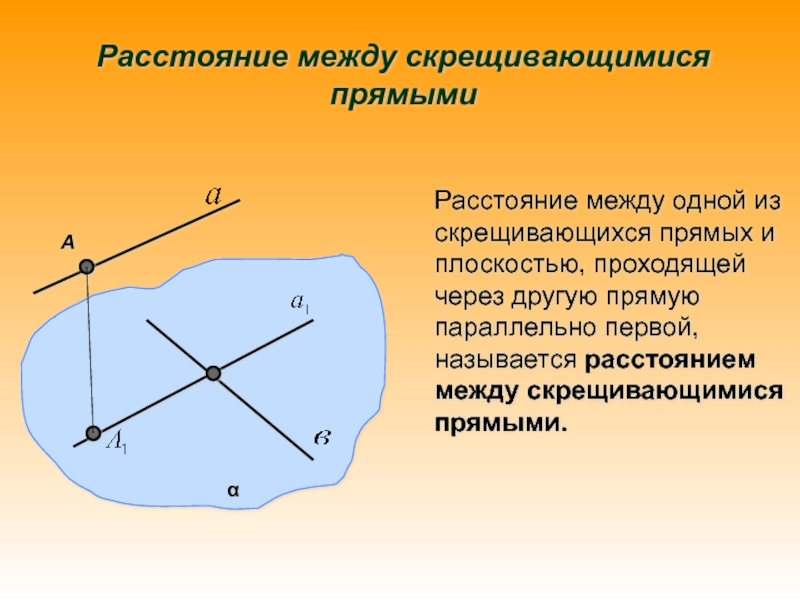
и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием

между скрещивающимися прямыми.

перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к

самой наклонной.

Дано:

АМ – наклонная к пл.

НМ – проекция наклонной,

Доказать:

А

Н

М

α

β

Доказательство:

Значит, АН перпендикулярна любой прямой, лежащей в плоскости

По условию,

Тогда, прямая

перпендикулярна двум пересекающимся

прямым пл.

β

Значит,

β

(признак перпендикулярности

прямой и плоскости)

по определению

перпендикулярности прямой и плоскости.

НМ И АН.

основание наклонной перпендикулярно к ней , перпендикулярна и к её

проекции.

Задача 153, стр.45, дома разобрать самостоятельно.

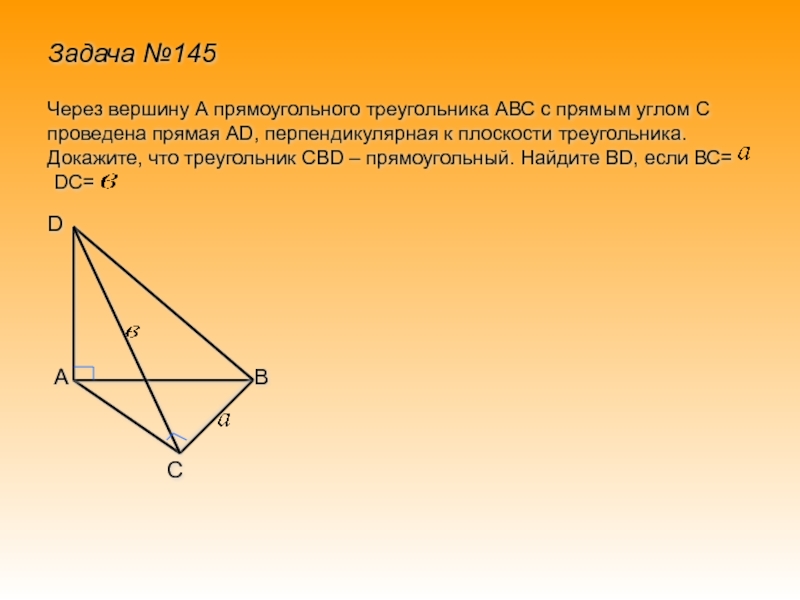
Слайд 17Задача №145Через вершину А прямоугольного треугольника АВС с прямым углом

С проведена прямая АD, перпендикулярная к плоскости треугольника. Докажите, что

треугольник СВD – прямоугольный. Найдите ВD, если ВС=

DC=

А

В

С

D

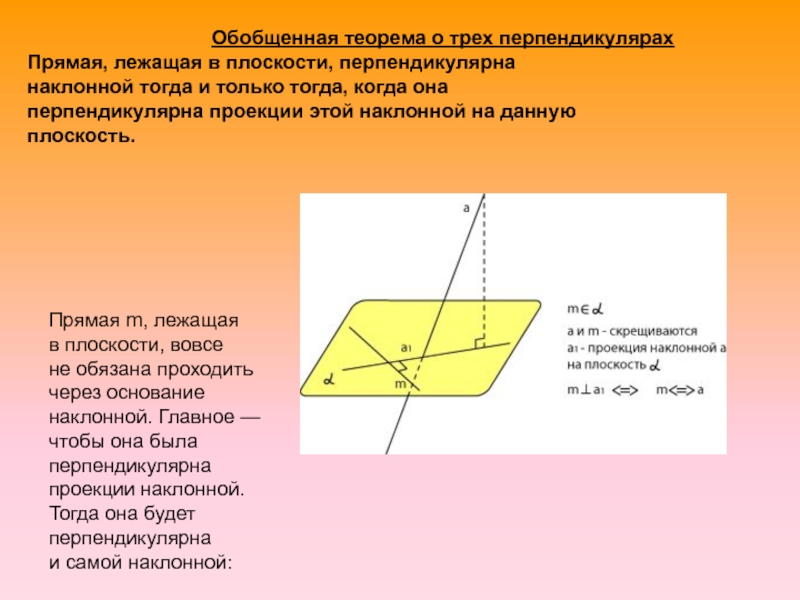
проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Обобщенная теорема о трех перпендикулярах

Векторы и их координаты

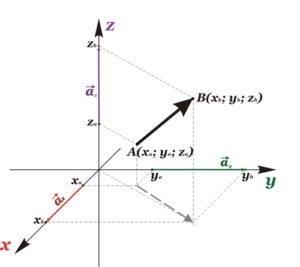          Вектор – это математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой.

          Мы можем «привязать» вектор к системе координат, т.е. мы можем его определять в пространстве координатами его проекций на координатные плоскости.

       Если даны две точки в пространстве А(x_a; y_a; z_a) и B(x_b; y_b; z_b), то дан и вектор 

, где а_х, а_у и а_z – координаты вектора.  Осталось определить значения а_х, а_у и а_z. 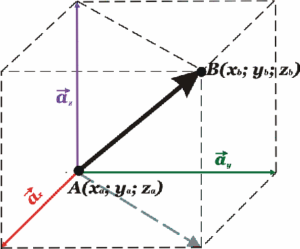Определяем:

а_х = x_b– x_a                       

а_у = y_b– y_a                       

а_z = z_b –  z_а                       

       Теперь, зная длины проекций вектора, мы можем легко найти длину вектора, которая, как видно из чертежа, есть не что иное, как диагональ параллелепипеда, сторонами которого являются координаты этого вектора. Его длина, модуль вектора, будет равна:

     А что есть длина вектора, как не расстояние между двумя точками: началом и концом вектора? То есть выведенная формула определяет расстояние между двумя точками в декартовой системе координат.

Задачи

Задача 1

Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная,

угол между которыми равен . 

а) Найти наклонную и ее проекцию на данную плоскость, если перпендикуляр равен d.

б) Найти перпендикуляр и проекцию наклонной, если наклонная равна m.

Рис. 6.

а) Дано:

Найти:

Решение:

Итак, имеем плоскость α, точку А, (рис. 6). Вспомним, перпендикуляром называется отрезок АН, который проведен из точки А к плоскости , АМ – наклонная.

Мы имеем треугольник АНМ. Этот треугольник прямоугольный. Для того чтобы найти гипотенузу АМ, нужно катет АН разделить на косинус прилежащего угла НАМ.

Найдем катет НМ.

Ответ: 

б) Дано:

Найти:

Решение:

АН перпендикуляр, АМ – наклонная, угол между ними , известна длина наклонной АМ. Нужно найти длину перпендикуляра АН и длину проекции НМ. 

Задача снова свелась к решению прямоугольного треугольника НАМ. Найдем катет АН.

Найдем катет HМ.

Ответ: 

Уравнения прямой и плоскости

           Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у. Это точки M(x_m; y_m) и N(x_n; y_n)

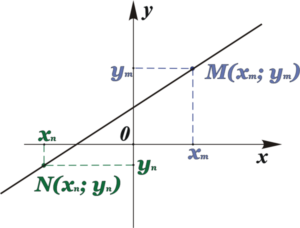          Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

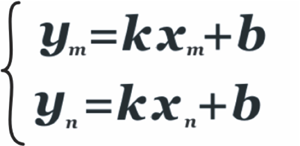
       Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении  этой системы.

        Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0,       (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

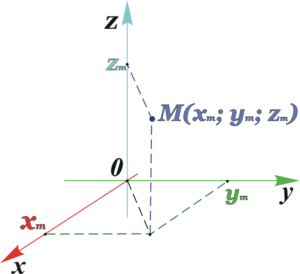        Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

       Уравнение прямой в пространстве задается через направляющий вектор. Но это уже не входит в рамки программы средней школы, поэтому просто принимаем к сведению.

            Если известны две точки пространства  M( x_m ; y_m ; z_m ) и  N( x_n ; y_n ; z_n ) , то уравнения прямой, проходящей через данные точки, выражаются формулами:

             Но вот что мы с вами можем, так это воспользоваться вектором этой прямой, который будет определяться расстоянием между точками в пространстве. И об этом подробно поговорим в следующем разделе — 

          Привязка фигур к  системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

  Ax + By + Cz + D = 0

 Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты  А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

       Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

       Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

         Плоскость можно провести через три точки, значит, и уравнений будет три!

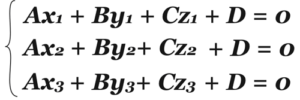
        Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда   вместо D   будет единица, а все остальные коэффициенты будут делиться на D,  назовем их также, А, В, С. И это уже вполне решаемая система!

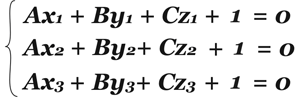
          Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

          Итак, точку описать можем, прямую описать можем, плоскость –  можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Аксиома плоскости (основная)

Другими словами, три точки, не лежащие на одной прямой, однозначно определяют плоскость:

На рисунке точки $A$, $B$ и $C$ лежат на плоскости $\alpha $. Поскольку эти точки не лежат на одной прямой, они однозначно задают эту плоскость. Обычно её так и обозначают: плоскость $ABC$.

Простой пример из жизни — стул на трёх ножках. Такого количества опор достаточно, чтобы он не качался и не падал. Плоскость стула задаётся однозначно благодаря всего трём точкам опоры.

Мы будем постоянно использовать эту аксиому для доказательства и решения задач. Ведь если удастся задать плоскость, то мы сведём трёхмерную задачу к двухмерной. А это радикально упрощает рассуждения.

Проверь себя

Задание 1. Выберите верное утверждение. 

1. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
2. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
3. Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
4. Ребра двугранного угла — это плоскости, которые его образуют. 

Задание 2. Угол между плоскостями — это…

1. Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
2. Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
3. Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
4. Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3. Что такое проекция прямой на плоскость?

1. Это любая прямая, проведенная из точки пересечения прямой и плоскости;
2. Это перпендикуляр, опущенный из любой точки на плоскость;
3. Это всегда точка пересечения прямой и плоскости;
4. Это прямая, образованная проекциями всех точек прямой на плоскость. 

Задание 4. Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?

1. Проекция будет равна этой прямой и параллельна ей;
2. Проекция будет меньше прямой и образовывать с ней угол;
3. Проекция будет точкой пересечения прямой и плоскости;
4. Проекция будет больше прямой и образовывать с ней угол.  

Задание 5. Как доказать, что прямая перпендикулярна плоскости?

1. Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
2. Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
3. Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
4. Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4

Решение задач

Аксиомы стереометрии часто применяются в доказательствах. И ещё в задачах с открытыми вопросами. Вот пример такой задачи:

Задача 1. Окружность и плоскость

Решение. Легко заметить, что ответ зависит от взаимного расположения точек $M$, $N$ и $O$.

Допустим, что все они лежат на одной прямой. Тогда $MN$ — диаметр, и вся окружность может как лежать в плоскости $\alpha $, так и не лежать в ней. Вот пример когда окружность не лежит в плоскости:

Пусть теперь точки $M$, $N$ и $O$ не лежат на одно прямой. По Аксиоме плоскости (Аксиома 4 в нашем списке) эти точки однозначно задают плоскость. Эта плоскость совпадает с плоскостью $\alpha $.

А поскольку окружность — плоская фигура, то остальные её точки также принадлежат плоскости $\alpha $:

Задача 2. Неравильный рисунок

Решение. Соединим точки $M$ и $K$ прямой $l$:

Мы видим, что точка $B\notin l$. Поэтому точки $M$, $B$, $K$ не лежат на одной прямой. И согласно Аксиоме плоскости (Аксиома 4 в нашем списке), эти точки однозначно задают плоскость.

С одной стороны, мы видим по рисунку, что это плоскость $\alpha $. С другой стороны, параллелограмм — плоская фигура, поэтому точки $M$, $B$, $K$ лежат ещё и в плоскости параллелограмма. А это значит, что плоскости $\alpha $ и $ABCD$ должны совпадать, чего на рисунке не происходит.

Есть и другой способ показать, что рисунок некорректен. По условию задачи, точки $M$, $B$, $K$ являются общими для плоскости $\alpha $ и плоскости $ABCD$. Согласно Аксиоме пересечения плоскостей (Аксиома 5 в нашем списке), все эти точки должны лежать на одной прямой.

Однако простое построение показывает, что точки $M$, $B$, $K$ не лежат на одной прямой, что противоречит аксиоме. Такое противоречие как раз и доказывает некорректность чертежа.

Далее мы будем лишь называть аксиомы — без нумерации.

Задача 3. Прямые на плоскости

Решение. Нарисуем прямые $a$, $b$, $c$ и обозначим их точки пересечения $M$, $N$, $K$:

Точки $M$, $N$, $K$ не лежат на одной прямой. По основной Аксиоме плоскости, эти три точки однозначно определяют некоторую плоскость $\alpha $.

Далее заметим, например, что точки $M\in \alpha $ и $N\in \alpha $ по построению. По основной Аксиоме прямой и плоскости вся прямая $MN=b$ лежит в этой плоскости, т.е. $b\subset \alpha $.

Аналогично доказывается, что прямые $a\subset \alpha $ и $b\subset \alpha $.

Задача 4. Пересечение плоскостей

Решение. Обозначим прямую, по которой пересекаются плоскости $\alpha $ и $\beta $, буквой $l$:

\

Дополнительное построение: прямая $AB$, которая пересекает прямую $l$ в точке $M$:

Точки $A\in \alpha $, $B\in \alpha $. По основной Аксиоме прямой и плоскости прямая $AB\subset \alpha $ — искомая линия сечения плоскости $\alpha $ и $ABC$.

Далее заметим, что точка $M\in l\subset \beta $. Дополнительное построение: прямая $CM$:

Точки $C\subset \beta $, $M\subset \beta $. И вновь по основной Аксиоме прямой и плоскости прямая $CM$ — искомая линия сечения плоскости $\beta $ и $ABC$.

Хочу отметить, что задачи на построение — это отдельный класс задач. Как в планиметрии, так и в стереометрии. Там много интересных моментов, им посвящены отдельные уроки. А то, что мы сделали сейчас — это совсем уж простые рассуждения, которые тем не менее опираются на всю мощь аксиом.

Задача 5. Стандартное доказательство

Решение. Это классическая задача на доказательство, которую в разных формулировках предлагают во всех учебниках по стереометрии.

Обозначим параллелограмм $ABCD$. Пусть $O$ — точка пересечения диагоналей.

Поскольку точка $O\notin AB$, точки $A$, $B$, $O$ не лежат на одной прямой. По основной Аксиоме плоскости эти три точки однозначно определяют плоскость. Обозначим эту плоскость $\alpha $.

Точки $A\in \alpha $, $O\in \alpha $. По основной Аксиоме прямой и плоскости, прямая $AO\subset \alpha $. Но точка $C\in AO\subset \alpha $. Следовательно, вершина параллелограмма $C\in \alpha $. Аналогично через точки $B$ и $O$ доказывается, что вершина $D\in \alpha $.

Замечание по поводу задач

Как видите, мы рассмотрели лишь самые простые задачи

Но даже на их примере видно, насколько важно чётко знать систему аксиом

Бесчисленное множество контрольных и экзаменов были завалены просто потому, что ученик не смог обосновать простые и наглядные рассуждения. Потому что, например, не знал: можно ли утверждать, что если две точки прямой лежат на плоскости, то и вся прямая лежит на этой плоскости.

В общем, учите аксиомы и практикуйтесь на простых примерах. А для более интересных задач нам потребуются некоторые следствия из этих аксиом. Чему и посвящён следующий урок.:)

1. Следствия из аксиом стереометрии
2. Теорема о трёх перпендикулярах
3. Комментарий к пробному ЕГЭ от 7 декабря
4. Метод Гаусса
5. Задачи про температуру и энергию звезд
6. Задача B4 про шерсть и свитер

4. Дополнение. Перпендикулярность прямой и плоскости

Далеко не всегда прямая, проходящая через «свободный» конец наклонной, будет перпендикулярна плоскости прямо по условию задачи. Поэтому вспомним определение и признак перпендикулярности:

Чтобы доказать, что прямая $l$ перпендикулярна плоскости $\alpha $, достаточно отыскать две пересекающиеся прямые $a\in \alpha $ и $b\in \alpha $ в этой плоскости и доказать, что обе эти прямые перпендикулярны исходной прямой $l$:

\

По этой теме будет отдельный урок. Сейчас просто отмечу, что большинство задач в стереометрии (особенно на доказательство) вполне решаются с помощью двух рассмотренных сегодня теорем: теорема о трёх перпендикулярах и признак перпендикулярности прямой и плоскости.

1. Следствия из аксиом стереометрии
2. 7 аксиом стереометрии
3. Локальная теорема Муавра — Лапласа
4. C2: расстояние между двумя прямыми
5. Задачи B2 на проценты: налоги и зарплата
6. Семья из трех человек (нестандартная задача)

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма \(ABCFDE\), ребра которой равны 2. Точка \(G\) — середина ребра \(CE\).

Докажите, что прямые \(AD\) и \(BG\) перпендикулярны.
Найдите расстояние между прямыми \(AD\) и \(BG\).

Решение:

Решим задачу полностью методом координат.

61.333. Расстояния

Расстояния

Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много

Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.

В стереометрии найти расстояние можно между следующими комбинациями фигур:

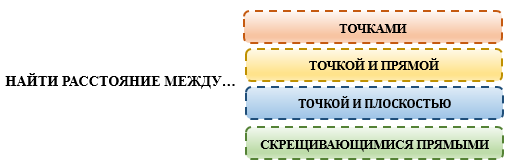
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ

Расстояние между точками– это длина отрезка, соединяющего эти точки.

В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.

То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.

РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ

Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.

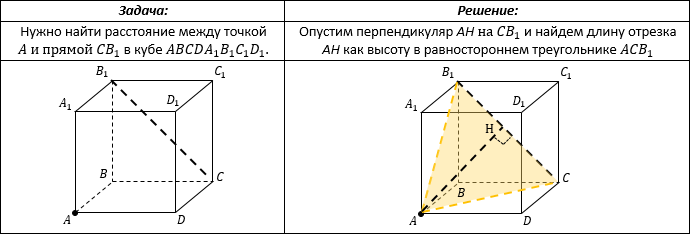
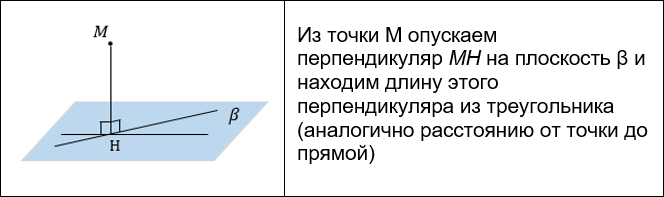
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ

Существует несколько способов нахождения расстояния от точки до плоскости:

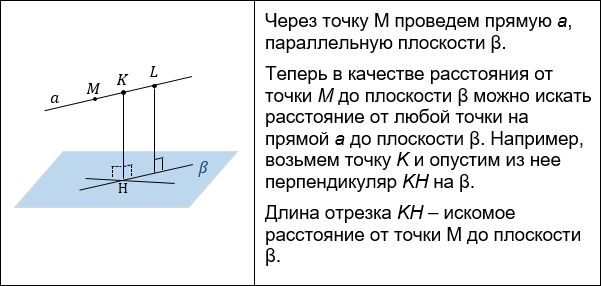
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Существует несколько способов нахождения расстояния между скрещивающимися прямыми:

1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.

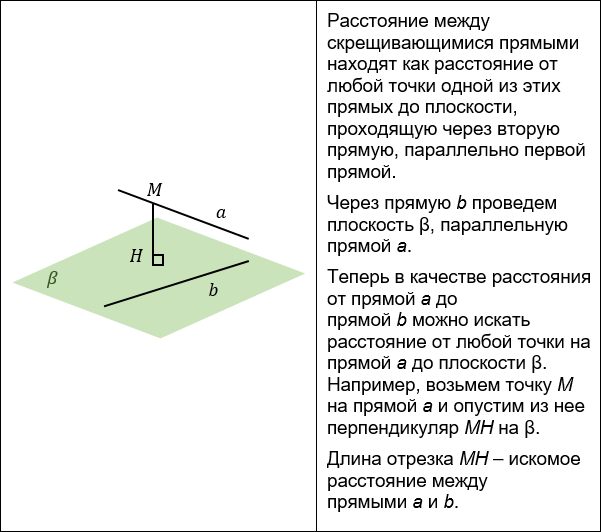
3. Построение параллельной плоскости.

Зачем нужны аксиомы

Математику изучают в школе не просто так. Большинство забудет все эти уравнения, графики и аксиомы сразу после ЕГЭ в 11 классе.

Задача школьного курса математики состоит в том, чтобы вы освоили научное мышление. Чтобы поняли, как работает наука, как проверяются гипотезы и как доказываются утверждения. И чем отличается частный жизненный опыт от универсальных знаний.

Подробнее о том, чем научное знание отличается от обывательского (и почему это так важно), смотрите в цикле уроков «Как работает наука». Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств

Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих

Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств. Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих.

Простой пример «очевидного» утверждения. Биссектриса треугольника пересекает его противоположную сторону:

Спасибо, Капитан Очевидность. Однако напрямую этот факт ниоткуда не следует. Его можно доказать, например, через тригонометрию или координаты. Но потребовать такое доказательство — отличная задача-гроб на устном экзамене в университет.

Создание системы аксиом — долгий и кропотливый процесс. Классическая евклидова геометрия, которую изучают в школе, основана на аксиомах, которые формировались более двух тысяч лет. Основоположник этих аксиом — Евклид — жил в III веке до н.д. Собственно, потому геометрия и называется евклидовой.

Зато когда система аксиом построена, все последующие теоремы выводятся из неё через логические рассуждения. Без привлечения наглядных иллюстраций и «очевидных соображений». Вот здесь и начинается настоящая наука.:)

Метод координат

•  Расстояние между точками  А(x_a; y_a; z_a)  и B(x_b; y_b; z_b) выражается формулой, показанной в предыдущей главе:
•   Расстояние от точки   M(x_m; y_m;z_m)  до плоскости α, заданной общим уравнением  Ax + By + Cz + D = 0, может быть вычислено по формуле: 
•  Расстояние между параллельными плоскостямии  α₁ и α₂  (α₁:  Ax + By + Cz + D₁ =0   и   α₂:  Ax + By + Cz + D₂ = 0) вычисляется по формуле:
•   Угол между скрещивающимися прямыми. Косинус угла между ними (острого) определяется по декартовым координатам векторов этих прямых:Тогда формула приобретает следующий вид:
•  Угол между плоскостями α и β, заданными уравнениями можно найти с помощью следующей формулы:

Фактчек

• Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. 
• Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны. 
• Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°. 
• Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым. 
• Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b. 

Аксиома разбиения (дополнительная)

Интуитивно эта аксиома вполне очевидна. Если две точки лежат по разные стороны от плоскости $\alpha $, то отрезок, соединяющий эти точки, неизбежно пересечёт плоскость $\alpha $. И наоборот: если точки лежат по одну сторону от плоскости $\alpha $, то отрезок, их соединяющий, не пересечёт эту плоскость.

На рисунке мы видим, что отрезок $AB$ пересекает плоскость $\alpha $ в точке $M$, поскольку точки $A$ и $B$ лежат по разные стороны от $\alpha $. И наоборот: отрезок $AC$ не пересекает плоскость $\alpha $, поскольку точки $A$ и $C$ лежат по одну сторону от плоскости.

Здесь можно долго рассуждать, что плоскость $\alpha $ делит всё пространство на два полупространства. Что эта плоскость является границей для таких полупространств. Но это уже аналитическая геометрия и топология — сейчас не будем залезать в дебри.

Углы между плоскостями

Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели. 

Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия. 

Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла. 

Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. 

Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке: АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;a, b  — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.  

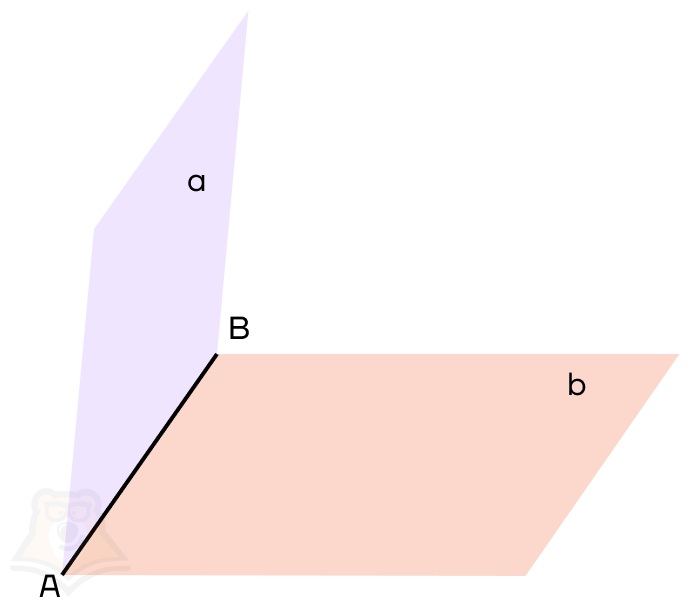
Как мы сталкиваемся с двугранными углами, когда читаем книгу?Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.

Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.

Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости

Важно, чтобы перпендикуляры пересекались в одной точке

Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.

Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. 

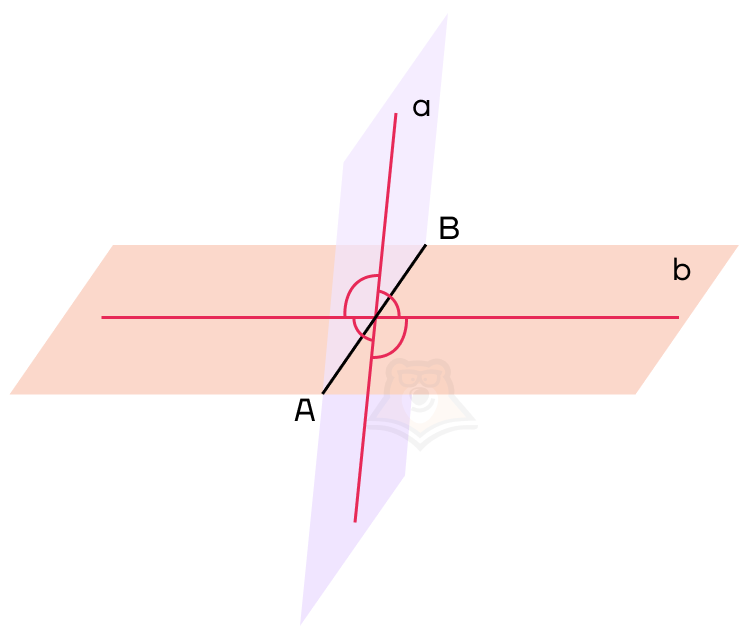
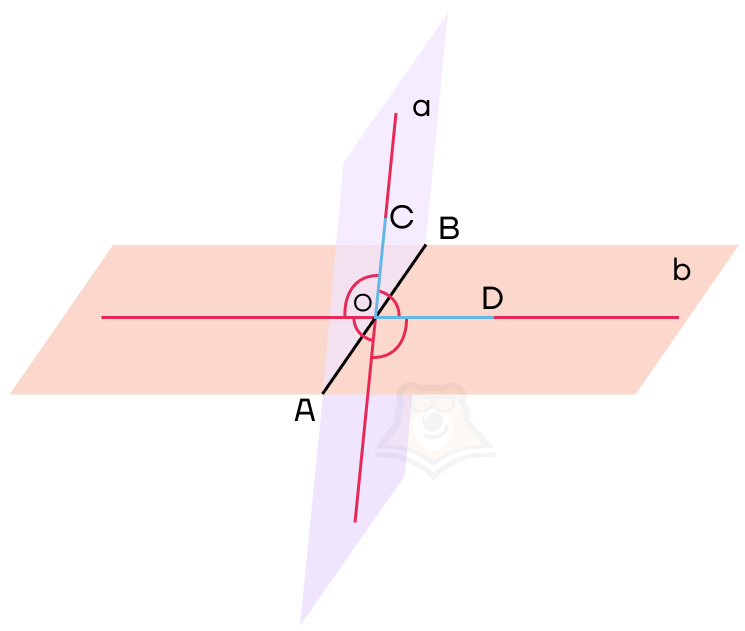
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями. 

Угол COD также будет называться линейным углом двугранного угла. 

Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой. 

Как и обычные углы, углы между плоскостями бывают трех видов:

• Острые, то есть меньше 90
• Прямые, равные 90
• Тупые, которые больше 90и меньше 180

Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.

А что будет, если между плоскостями получится прямой угол?

Такие плоскости называются перпендикулярными. 

Где в комнате можно найти перпендикулярные плоскости?Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.

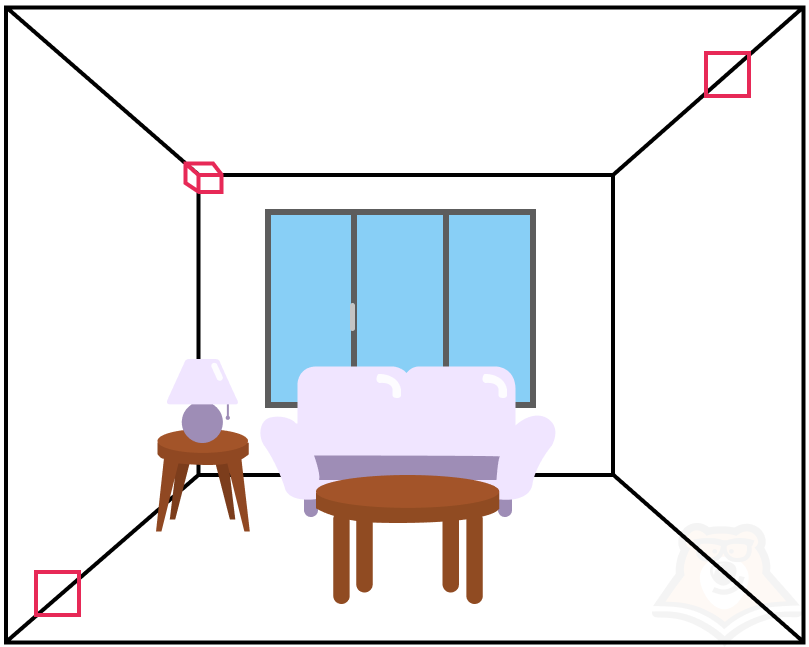
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам. 

Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму. 

Алгоритм нахождения угла между плоскостями1 шаг. Найти линию пересечения плоскостей.2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости. 3 шаг. Найти острый угол между построенными перпендикулярами.

Проверь себя

Задание 1. Как найти расстояние между точкой и прямой?

1. Найти длину любой линии от этой точки до прямой.
2. Найти длину перпендикуляра, опущенного из этой точки на прямую.
3. Невозможно найти расстояние между точкой и прямой.
4. Ни один из вышеперечисленных вариантов. 

Задание 2. Как найти расстояние между скрещивающимися прямыми?

1. Найти длину произвольной прямой между ними.
2. Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
3. Найти длину их общего перпендикуляра.
4. Невозможно найти расстояние между скрещивающимися прямыми. 

Задание 3. Как найти расстояние от точки до плоскости?

1. Найти длину перпендикуляра, опущенного из этой точки на плоскость.
2. Найти длину произвольной линии, проведенной из точки к плоскости.
3. Найти расстояние от точки до любой прямой, лежащей в плоскости.
4. Невозможно найти расстояние между точкой и плоскостью.

Задание 4. Как найти расстояние от прямой до плоскости?

1. Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
2. Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
3. Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
4. Невозможно найти расстояние между прямой и плоскостью. 

Задание 5. Как найти расстояние между параллельными плоскостями?

1. Невозможно найти расстояние между параллельными плоскостями.
2. Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
3. Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
4. Найти длину отрезка, соединяющего две произвольные прямые в плоскостях. 

Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2

Что такое расстояние от точки до плоскости

Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость.

Рассмотрим плоскость \(\alpha\) и точку А, не принадлежащую этой плоскости. Проведем из точки А перпендикуляр к плоскости \(\alpha\), и обозначим буквой H точку пересечения этой прямой с плоскостью. Тогда отрезок АН является перпендикуляром, проведенным из точки А к плоскости \(\alpha\), а точка Н — основанием перпендикуляра. Поставим в плоскости \(\alpha\) произвольную точку М, различную с Н, и проведем отрезок AM. Этот отрезок называют наклонной, проведенной из точки А к плоскости \(\alpha\), а точка М основанием наклонной. Отрезок HM — проекция наклонной на плоскость \(\alpha\).

Рассмотрим прямоугольный треугольник АМН: сторона АН — катет, а сторона AM — гипотенуза, значит АН<АМ. Получаем, что, перпендикуляр проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Следовательно, наименьшим из всех расстояний от точки А до различных точек плоскости \(\alpha\) будет расстояние до точки H, то есть отрезок АН. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости \(\alpha\), называется расстоянием от точки А до плоскости \(\alpha\).

С помощью этих рассуждений разберем следующую теорему.

Что такое расстояние между прямыми в пространстве

Для начала дадим определение этому понятию.

Определение

Расстояние между прямыми в пространстве — это отрезок, который соединяет две прямые линии по самому короткому пути. Иными словами, он перпендикулярен обеим этим прямым.

Но не всегда две линии могут быть параллельны друг другу.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Определение

Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую параллельно первой.

Таким образом, чтобы найти расстояние между этими скрещивающимися прямыми, нужно от одной из прямых провести перпендикуляр на плоскость, в которой лежит другая прямая.

Между параллельными прямыми расстояние одинаково на протяжении всей их длины: перпендикуляр, опущенный из любой точки одной из этих линий, всегда будет одной и той же величины.