Скрещивающиеся прямые

Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми

Скрещивающиеся прямые

Нам известны два случая расположения прямых в пространстве a ∩ b; а || b. Общее для них: они лежат в одной плоскости (рис. 1, 2).

(по следствию из аксиомы)

(по определению параллельных прямых)

ЗАДАНИЕ №1 в рабочей тетради

Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).

Доказать, что АВ скрещивается с CD.

Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.

Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.

ЗАДАНИЕ №2 в рабочей тетради

Теорема :

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.

Дано: АВ скрещивается CD (рис. 6).

Построить α: АВ ⊂ α, CD || α.

1. Через точку А проведем прямую АЕ, АЕ || CD.

В доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.

Задание №3-№4 в рабочей тетради

Углы с сонаправленными сторонами. Угол между прямыми

Любая прямая а, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей.

Скрещивающиеся прямые

Через две пересекающиеся или параллельные прямые можно провести плоскость, и притом единственную. Возможна также ситуация, когда через две прямые плоскость провести нельзя.

Две прямые называются скрещивающимися, если они не параллельны и не пересекаются.

Другими словами, две прямые скрещиваются, если они не лежат в одной плоскости, так как прямые, лежащие в одной плоскости, обязательно будут либо пересекаться, либо параллельны.

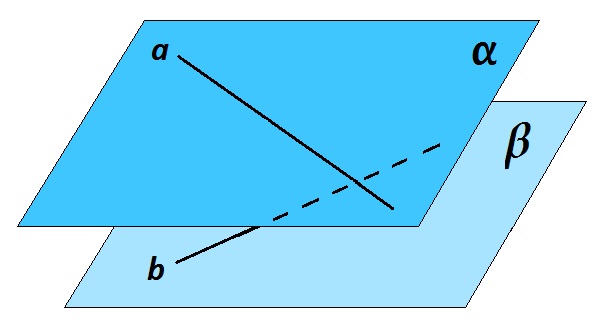
Прямые a и b на рисунке скрещиваются

Важно, что через две скрещивающиеся прямые можно провести две параллельные плоскости. Причем это единственная пара плоскостей

Теорема 2

Если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые — скрещивающиеся. 

Доказательство:

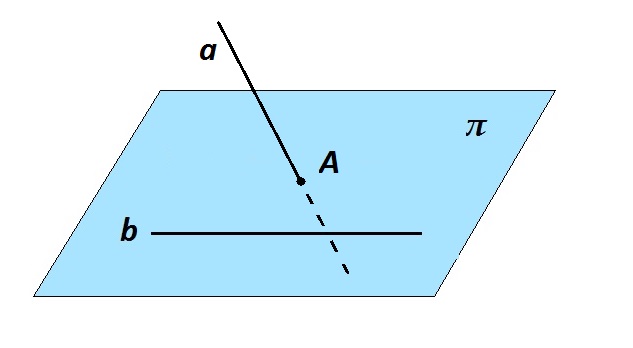
Пусть a и b — прямые, b лежит в плоскости π, a пересекает плоскость π в точке A. А не принадлежит прямой b. Используем метод доказательства от противного. Предположим, что прямые a и b лежат в одной плоскости. В этом случае данная плоскость проходит через прямую b и точку А, то есть она совпадает с плоскостью π.
Прямая a не может одновременно находиться в плоскости π и пересекать ее в одной точке, как дано по условию.  Теорема доказана.

Теорема 3

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство:

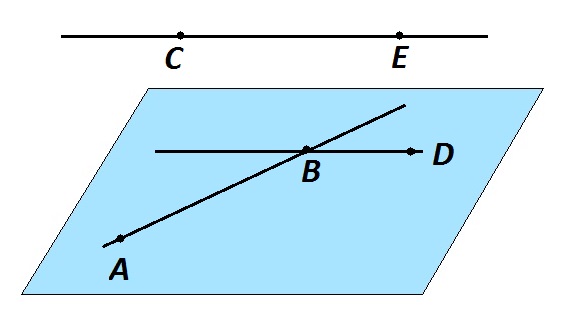
Рассмотрим скрещивающиеся прямые AB и CЕ.

1. Через точку D можно провести прямую ВD параллельную СЕ.
2. Через пересекающиеся прямые BD и AB можно провести плоскость.
3. Так как прямая CE не лежит в этой плоскости и параллельна прямой BD, то она параллельна и данной плоскости. Эта плоскость единственная.

Теорема доказана.

Практическое применение

Теоретические основы, понятия на уроках геометрии в режиме онлайн понятны, но для закрепления материала в классе решаются разные задачи с доказательствами. Сначала нужно найти в пространстве линии, углы и охарактеризовать их вид.

Типовые задачи

Чтобы на практике понять действие теорем, нужно использовать пример решения и наглядный рисунок. Например, точка D не лежит в плоскости АВС, точки M, N, P будут центром DA, DB и DC. Точка К расположена на прямой ВС. Требуется определить взаимное расположение линий.

Линии будут обозначаться буквами АВ и BD, они находятся в плоскости АВD и пересекаются.

Эти две линии расположены в единой плоскости, поэтому являются параллельными или пересекающимися. Нужно провести среднюю линию NP, где N, P являются серединой отрезка DB и DC. По свойству средней линии, NP II (знак параллельности) ВС. Через т. Р проводится отрезок, II ВС, и это NP. Любая другая линия, проходящая через т. Р, не II ВС, поэтому PK и ВС пересекаются.

В треугольнике ABD точки M и N являются центрами сторон АD и ВD, значит, МN — средняя линия. Основываясь на типовых свойствах, МN II АВ.

В ADС точки M и Р будут серединами АD и СD. Значит, МР является средней линией. МР IIАС.

Прямопроходящая линия КN и ВD являются одной и той же прямой. АС располагается в плоскости АВС, линия ВD пересекает АВС в точке, не расположенной на АС. По признаку ВD и АС являются скрещивающимися, КN и АС — такая же.

MD и АD будут одинаковой ПЛ по всем характеристикам и параметрам. Линия ВС располагается в плоскости АВС, прямая АD пересекает АВС в точке, расположенной в стороне от ВС. АD и ВС относятся к скрещиванию, а МD и ВС такие же.

Сложные задания

В нижней части пирамиды SABC расположена геометрическая фигура с прямым углом при вершине С, гипотенузой АВ = 13 и катетом АС = 12 (когда 1 из 2 сторон прямоугольного треугольника образует прямой угол). Максимальная точка пирамиды S проектируется в основании В. Боковое ребро CS равняется 5*корень из 5. Требуется выяснить расстояние между ребрами AS и ВС.

Для решения нужно определить расстояние между отрезками AS и ВС. Они лежат на скрещивающихся прямых (СП). Точка s не принадлежит отрезку АВС, а точка А принадлежит АВС. AS пересекает АВС, ВС включает отрезок АВС и А не принадлежит ВС.

Расстояние между 1 из СП и плоскостью, проложенной через другую II первой, называется промежутком между СП. Нужно построить такое пространство, проходящее через 1 из СП, параллельно другой, и добавить перпендикуляр к пространству из точки, принадлежащей другой линии.

Пирамиду нужно достроить до параллелепипеда, через т. А на плоскости АВС проведя параллельную ВС и через т. В — АС. Точку пересечения ПЛ обозначают буквой D. Через А, С, D нужно провести прямые II SB, на каждой отложить отрезки, равные BS, а точки соединить линиями.

Определение скрещивающихся прямых подтверждено теоремами, также существует условие, описывающее, что через каждую пару ПЛ, которые скрещены, проложена плоскость, II другой линии. Изучены случаи расположения ПЛ в пространстве: они пересекаются, являются параллельными или скрещиваются.

Угол между скрещивающимися прямыми

2) Скрещивающиеся прямые

Пусть прямые а и b скрещивающиеся. Выберем произвольную точку О. Через точку О проведем прямую а₁, параллельную прямой а, и прямую b₁, параллельную прямой b (Рис. 5.). Прямые а₁ и b₁ пересекаются в точке О. Угол между двумя пересекающимися прямыми а₁ и b₁, угол φ, и называется углом между скрещивающимися прямыми.

Рис. 5. Угол между двумя скрещивающимися прямыми

Зависит ли величина угла от выбранной точки О? Выберем точку О₁. Через точку О₁ проведем прямую а₂, параллельную прямой а, и прямую b₂, параллельную прямой b (Рис. 6.). Угол между пересекающимися прямыми а₂ и b₂ обозначим φ₁. Тогда углы φ и φ₁ — углы с сонаправленными сторонами. Как мы доказали, такие углы равны между собой. Значит, величина угла между скрещивающимися прямыми не зависит от выбора точки О.

Рис. 6.

Задача 1. Найти угол между двумя прямыми

Прямые ОВ и СD параллельны, ОА и СD скрещиваются. Найдите угол между прямыми ОА и СD, если: 

Выберем точку С. Через нее проходи прямая СD. Проведем СА₁ параллельно ОА (Рис. 7.). Тогда угол А₁СD – угол между скрещивающимися прямыми ОА и СD. По теореме об углах с сонаправленными сторонами, угол А₁СD равен углу АОВ, то есть 40.

Рис. 7. Найти угол между двумя прямыми

Сделаем то же самое построение (Рис. 8.). Тогда угол между скрещивающимися прямыми ОА и СD равен 45, так как он наименьший из углов, которые получаются при пересечении прямых СD и СА₁.

Рис. 8. 

Сделаем то же самое построение (Рис. 9.). Тогда все углы, которые получаются при пересечении прямых СD и СА₁ равны 90. Искомый угол равен 90.

Рис. 9.

Задача 2

1) Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.

Рис. 10. 

Доказательство

Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно (Рис. 10.). Нужно доказать, что MNKL – параллелограмм.

Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине.

Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине.

И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых.

Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.

2) Найдите угол между прямыми АВ и СD, если угол МNК = 135.

Как мы уже доказали, МN параллельна прямой АВ. NК – средняя линия треугольника АСD, по свойству, NК параллельна DС. Значит, через точку N проходят две прямые МN и NК, которые параллельны скрещивающимся прямым АВ и DС соответственно. Значит, угол между прямыми МN и NК является углом между скрещивающимися прямыми АВ и DС. Нам дан тупой угол МNК = 135. Угол между прямыми МN и NК – наименьший из углов, полученных при пересечении этих прямых, то есть 45 .

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где \(A,B,C,D\) – какие-то числа.

Если найти \(A,B,C,D\), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

Получилась система из трех уравнений, но неизвестных 4: \(A,B,C,D\). Если наша плоскость не проходит через начало координат, то мы можем \(D\) приравнять \(1\), если же проходит, то \(D=0\). Объяснение этому простое: вы можете поделить каждое ваше уравнения на \(D\), от этого уравнение не изменится, но вместо \(D\) будет стоять \(1\), а остальные коэффициенты будут в \(D\) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости \(D=1\):
$$\begin{cases} A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end{cases}$$
$$\begin{cases} A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end{cases}$$
$$\begin{cases} A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end{cases}$$
$$\begin{cases} A=-0.5,\\ B=-1, \\ C=0.5.\end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Теорема 1 (признак скрещивающихся прямых) и ее доказательство

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Доказательство

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Рис. 1.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

Общая характеристика

Алгоритм определения того, что прямые линии (ПЛ) могут называться скрещивающимися, описывает расположение вне бесконечной поверхности. Существует несколько теорем и доказательств пересечения прямых в одной точке.

Основные понятия и теоремы

Из курса планиметрии известно, что две ПЛ в плоскости пересекаются, имеют одну точку или располагаются параллельно по отношению друг к другу.

Произвести вычисления, необходимые расчеты и графическое построение можно, изучив главные особенности и характеристику понятий. Когда прямые заданы векторными параметрическими уравнениями, выполняется равенство (формула) р = р0+SU и r = r0+tv.

Вычисление удаленности между ними определяется смешанным и векторным произведением D = (r 0 — p 0, u, v)/u, v.

Существует первая теорема, доказывающая признаки скрещивающихся ПЛ. Ее смысл заключается в теоретическом аспекте, указывающим на то, что когда одна из двух ПЛ расположена в плоскости, а другая ПЛ пересекает пространство в точке, не находящейся на отрезке, то эти ПЛ являются скрещивающимися. Данные можно доказать графически, используя методы черчения и рисования фигур, углов и перпендикуляров.

Например, дана плоскость α, в ней находится АВ, а прямая CD пересекается с плоскостью в т. С, расположенной на АВ. Для доказательства скрещивания прямых используется метод от обратного. Предполагается, что существует вторая плоскость, в которой расположены AB и DC. Во второй плоскости лежит отрезок АВ и т. С. Через ПЛ и точку, не лежащую на ней, проходит плоскость альфа. Второй плоскости бета не существует. Прямые скрещиваются.

Существует три положения прямых. В первом случае линии a и b пересекаются в т. С. Сквозь 2 ПЛ, которые пересекаются, проходит плоскость. ПЛ А II В, лежат в едином пространстве и не смогут пересечься. Прямые скрещиваются, когда не находятся в едином поле.

Вторая теорема о скрещивающихся прямых гласит, что через каждую из пары скрещивающихся ПЛ проходит одна плоскость, параллельная другой. Для подтверждения даны две ПЛ AB и CD. Требуется доказать, что через линию АВ проложена плоскость, параллельная СД.

Для этого через точку А проводится линия АЕ, расположенная параллельно DC. Согласно теореме о параллельных ПЛ, эта линия является единственной. Пересечение двух линий АВ и АЕ позволяет проложить плоскость альфа. Прямая DC, не лежащая в пространстве альфа, II АЕ, значит, DC параллельна пространству α.

Для доказательства единства такого пространства предполагается, что существует другая плоскость бета (β), проходящая через АВ, и является параллельной по отношению к DC.

Особенности ПЛ:

Прочие условия

У отрезков, которые скрещиваются, нет общей точки соприкосновения, потому что тогда они бы располагались в едином пространстве.

Признаки скрещивающихся прямых:

В тригонометрии еще существует понятие обозначения косинуса — это отношение длины стороны, прилежащей к острому углу, к гипотенузе. Осуществить нахождение ПЛ параллельно скрещивающимся можно через произвольную точку. Это официальное утверждение. Две ПЛ могут быть параллельными или пресекать плоскость, значит, они находятся в едином пространстве координат.

https://youtube.com/watch?v=jEQseQZnERg

Теорема о равенстве углов с сонаправленными сторонами

Если стороны двух углов сонаправленны, то такие углы равны.

Доказательство

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОВ и О₁В₁ (Рис. 2.). То есть, мы имеем два угла АОВ и А₁О₁В₁, чьи стороны лежат на сонаправленных лучах. Докажем, что эти углы равны.

Рис. 2.

На стороне луча ОА и О₁А₁ выберем точки А и А₁ так, чтобы отрезки ОА и О₁А₁ были равны. Аналогично, точки В и В₁ выберем так, чтобы отрезки ОВ и О₁В₁ были равны.

Рассмотрим четырехугольник А₁О₁ОА (Рис. 3.). В этом четырехугольники стороны ОА и О₁А₁ параллельны и равны. По признаку параллелограмма, четырехугольник А₁О₁ОА является параллелограммом. Так как А₁О₁ОА – параллелограмм, то стороны ОО₁ и АА₁ параллельны и равны.

Рассмотрим четырехугольник В₁О₁ОВ. В этом четырехугольники стороны ОВ и О₁В₁ параллельны и равны. По признаку параллелограмма, четырехугольник В₁О₁ОВ является параллелограммом. Так как В₁О₁ОВ – параллелограмм, то стороны ОО₁ и ВВ₁ параллельны и равны.

Рис. 3.

И прямая АА₁ параллельна прямой ОО₁, и прямая ВВ₁ параллельна прямой ОО₁, значит прямые АА₁ и ВВ₁ параллельны.

Рассмотрим четырехугольник В₁А₁АВ. В этом четырехугольники стороны АА₁ и ВВ₁ параллельны и равны. По признаку параллелограмма, четырехугольник В₁А₁АВ является параллелограммом. Так как В₁А₁АВ – параллелограмм, то стороны АВ и А₁В₁ параллельны и равны.

Рассмотрим треугольники АОВ и А₁О₁В₁. Стороны ОА и О₁А₁равны по построению. Стороны ОВ и О₁В₁ также равны по построению. А как мы доказали, и стороны АВ и А₁В₁ тоже равны. Значит, треугольники АОВ и А₁О₁В₁ равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А₁О₁В₁ равны, что и требовалось доказать.