Прямоугольный треугольник, свойства, признаки и формулы

Содержание

Слайд 1

Признаки равенства треугольников

Треугольник и его элементы
Задачи по теме «Первый признак равенства треугольников»
Задачи по теме «Второй признак равенства треугольников»
Задачи по теме «Третий признак равенства треугольников»
Справочный материал (формулировка теоремы и ее доказательство):
а) Первый признак равенства треугольников
б) Второй признак равенства треугольников
в) Третий признак равенства треугольников

pptcloud.ru
Слайд 2

D
N
L

Назовите:
1) сторону, лежащую против угла N :
2) сторону, лежащую против угла NDL:
3) угол, лежащий против стороны DN:
4) угол, лежащий против стороны DL:
5) углы, прилежащие к стороне NL: и

Треугольник

Рис. 1
Слайд 3

Первый признак равенства треугольников

M
F
N
L
O

Докажите, что OLF = OMN

Решение:
1) Рассмотрим OLF и :
а) OL =- по условию,
б) OF =- по условию,

Задача. Заполните пропуски.
Следовательно OLF = — по двум сторонам и углу между ними.
Рис. 2
в) LOF = — каквертикальные углы.
Слайд 4

B
S
A
R
Задача. Заполните пропуски.
S

Докажите, что ARS = BRS

а) Сторона = — по условию.
б) Сторона = — общая сторона.
в) = — по условию.
г) Следовательно, ARS = — по двум
и углу .
2) Т. к. ASR= BSR, то соответственные стороны и углы равны, BR = AR = 18 см, BRS = ARS =

15˚

Решение:

1) Рассмотрим ARS и

Рис. 3
Слайд 5

Второй признак равенства треугольников
Задача.
Докажите, что AXO = BZO

Решение:

A
X
B
Z
O

1) Рассмотрим BZO и
У них: а) Сторона = — по условию;
б) = — по условию;
в) = — как вертикальные.
Следовательно AXO = — по стороне и двум прилежащим к ней .

Рис. 4
Слайд 6

Задача.

F
B
D
A

На рисунке 5 луч DF биссектриса угла ADF
а) Докажите, что ADF = BDF;
б) Найдите сторону BD и DBF.
Решение:
а) Рассмотрим ADF и .
У них: 1) = — общая сторона;
2) = — по условию;
3) = , так как DF –
17 дм

110˚

биссектриса ADB.
Следовательно, ADF = поиприлежащим к ней.
б) Из равенства треугольников следует равенство соответствующих сторон и углов,то есть сторона DB == дм, B = =.

˚
Рис. 5
Слайд 7

Третий признак равенства треугольников

A
N
B
C

108̊
а) Докажите, что CAN = BAN
б) Найдите ABN.

Решение:
а) Рассмотрими BAN.
У них: 1) AC = — по условию;
2) CN = — по условию;
3) AN = AN – общая сторона.
Значит, CAN = — по трем .
б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то естьABN = = .
Рис. 6

˚
Слайд 8

Рассмотрим треугольники ABC и DEF, у которых AB=DE, AC=DF, углы A и D равны (рис. 7). Докажем, что ABC= DEF.
Так как A=D, то треугольник ABC можно наложить на треугольник DEF так, что вершина A совместится с вершиной D, а стороны AB и AC наложатся соответственно на лучи DE и DF. Поскольку AB=DE, AC=DF, то сторона AB совместится со стороной DE, а сторона AC – со стороной DF; в частности, совместятся точки B и E, C и F. Следовательно, совместятся стороны BC и EF. Итак, треугольники ABC и DEF полностью совместятся, значит, они равны.

Рис. 7
C
A
B
D
E
F

Теорема

Доказательство

Теорема доказана.
Слайд 9

Теорема
Рассмотрим треугольники ABC и DEF, у которых AB=DE, A= D, B= E (рис. 8). Докажем, что ABC= DEF.
Наложим треугольник ABC на треугольник DEF так, чтобы вершина A совместилась с вершиной D, сторона AB – с равной ей стороной DE, а вершины C и F оказались по одну сторону от прямой DE.
Так как A=D и B= E, то сторона AC наложится на луч DF, а сторона BC – на луч EF. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче DF, так и на луче EF и, следовательно, совместится с общей точкой этих лучей – вершиной F. Значит, совместятся стороны AC и DF, BC и EF.
Итак, треугольники ABC и DEF полностью совместятся, поэтому они равны.
Теорема доказана.

C
A

B

Рис. 8
D
E
F

Доказательство
Слайд 10

Теорема
Доказательство
Рассмотрим треугольники ABC и DEF, у которых AB = DE, BC = EF, CA = FD (рис. 9). Докажем, что ABC = DEF. Приложим треугольник ABC к треугольнику DEF так, чтобы вершина A совместилась с вершиной D, вершина B – с вершиной E, а вершины C и F оказались по разные стороны от прямой DE (рис. 10).
Возможны три случая: луч FC проходит внутри угла DFE (рис. 10, а); луч FC совпадает с одной из сторон этого угла (рис. 10, б); луч FC проходит вне угла DFE (рис. 10, в). Рассмотрим первый случай (остальные случаи можете рассмотреть самостоятельно).
Так как по условию теоремы стороны AC и DF, BC и EF равны, то треугольники DFC и EFC – равнобедренные (см. рис. 10, а). По теореме о свойстве углов равнобедренного треугольника 1 = 2, 3 = 4, поэтому DCE = DFE. Итак, AC = DF, BC = EF,C = F.
Следовательно, треугольники ABC и DEF равны по первому признаку равенства треугольников.
Теорема доказана.

Рис. 9

A
C
B

F
D
E

D (A)
C
F
E (B)

D (A)
E (B)
C
F
Рис. 10
а)
б)

в)

E (B)
C
F
D (A)

1

3

2
4

Посмотреть все слайды

Прямоугольный треугольник

Ключевые слова: треугольник, прямоугольный, катет, гипотенуза, теорема Пифагора, окружность

Треугольник называют прямоугольным, если у него есть прямой угол.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.

По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
Сумма двух острых углов прямоугольного треугольника равна прямому углу.
Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = h_c из вершины С его прямого угла.

Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.

Все три треугольника АВС, АСD и ВСD подобны между собой.

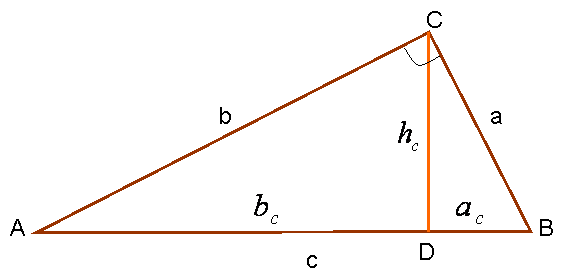Из подобия треугольников определяются соотношения:

$$h = \sqrt{a_{c} \cdot b_{c}} = \frac{a \cdot b}{c}$$;
c = a_c + b_c;
$$a = \sqrt{a_{c} \cdot c}, b = \sqrt{b_{c} \cdot c}$$;
$$(\frac{a}{b})^{2}= \frac{a_{c}}{b_{c}}$$.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a2 + b2 = c2

Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что
a2 + b2 = c2,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Признаки равенства прямоугольных треугольников:

по катету и гипотенузе;
по двум катетам;
по катету и острому углу;
по гипотенузе и острому углу.

См. также: Площадь треугольника, Равнобедренный треугольник, Равносторонний треугольник

Пример 2

Пример 2: Задача 277 из учебника «Геометрия 7-9». Автор — Атанасян Л.С.

Расстояние между параллельными прямыми a и b равно 3 см, а расстояние между параллельными прямыми a и c равно 5 см. Найдите расстояние между параллельными прямыми b и c

Решение:

Рис. 5. Чертёж к примеру 2 (первый случай)

Поскольку , то = 5 – 3 = 2 (см).

Однако данный ответ неполный. Существует и другой вариант расположения прямых на плоскости:

Рис. 6. Чертёж к примеру 2 (второй случай)

В данном случае .

Ответ: 2 см, 8 см.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/sootnosheniya-mezhdu-storonami-i-uglami-treugolnikov/rasstoyanie-ot-tochki-do-pryamoy-rasstoyanie-mezhdu-parallelnymi-pryamymi

https://www.youtube.com/watch?v=nSMjwuADyUg

http://www.cleverstudents.ru/line_and_plane/parallel_lines.html

http://proteacher.ru/2015/01/18/rasstoyanie_mezhdu_parallelnymi_pryamymi_1421587644_88852.rar

http://fs00.infourok.ru/images/doc/195/223344/img8.jpg

http://www.yaklass.ru/p/geometria/7-klass/sootnoshenie-mezhdu-storonami-i-uglami-treugolnika-9155/priamougolnye-treugolniki-9175/re-cef42b35-127b-4350-ac33-e249179f4160

http://cs1-26v4.vk-cdn.net/p15/f1c21f09bd9fad.mp3?extra=u96JCzuBb-XdruFah977CJD_izMWWpkY6XMumaQX91DaN6oYjpkhgbiIWHT_JgbeMV8sBTXjR7DNV22iBzUUOuBrsARIHPev

http://www.flconf.org/education/wp-content/uploads/2011/04/5107103-1886×2550-1-1024×757.jpg

Понятие расстояния между точкой и прямой

Ранее мы принимали за расстояние между двумя точками длину отрезка, соединяющего их. То есть утверждения «отрезок НВ равен 5 см» и «расстояние между точками Н и В равно 5 см» эквиваленты друг другу. Однако в геометрии расстояние можно определить и между точкой и прямой.

Рассмотрим некоторую прямую b и произвольную точку А, не лежащую на ней. Опустим из точки перпендикуляр на прямую, и точку их пересечения обозначим как Н. Также отметим на прямой точку М, не совпадающую с Н, и соединим ее с А:

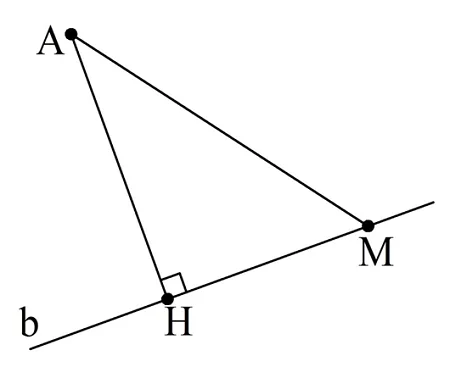
В результате мы получаем прямоугольный треуг-к АНМ. Так как АМ – гипотенуза, то она длиннее катета АН:

AM > AH

Прямую АМ называют наклонной к прямой, а АН – это перпендикуляр. Получаем, что перпендикуляр из точки всегда короче, чем наклонная. Именно длину перпендикуляра называют расстоянием между точкой и прямой. Другими словами, расстояние между прямой и точкой – это наименьшая возможная длина отрезка, соединяющего эту точку с прямой.

Задание. Докажите, что середина основания р-бедр. треуг-ка равноудалена от боковых сторон треугольника.

Решение. Обозначим вершины треуг-ка буквами А, В и С, причем АС – основание. Буквой Н обозначим середину АС. Естественно, что АН = НС. Теперь опустим из Н перпендикуляры на стороны АВ и ВС, которые обозначим как НМ и НЕ:

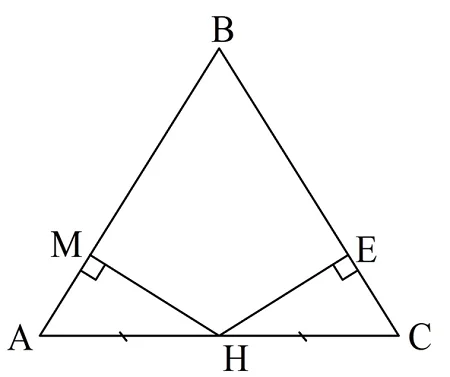
Нам необходимо доказать, что НМ = НЕ. Для этого сравним ∆АМН и ∆НЕС. Они прямоугольные. Их гипотенузы равны, ведь АН = НС. Также ∠А = ∠С, ведь это углы при основании равнобедренного треуг-ка. Значит, ∆АМН и ∆НЕС равны по равны по равному острому углу и гипотенузе. А из равенства треуг-ков следует, что МН = НЕ.

Задание. Докажите, что концы отрезка равноудалены от прямой, проходящей через середину этого отрезка.

Решение. Обозначим отрезок как АС, а его середину буквой Н. Опустим из А и С перпендикуляры АР и СМ на прямую, проходящую через Н:

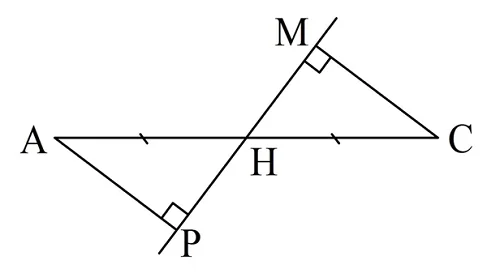
Требуется доказать, что АР = СМ. Рассмотрим ∆АНР и ∆МНС. Они прямоугольные, при этом АН = НС (по условию). Ясно, что ∠АНР = ∠МНС, ведь они являются вертикальными. Если у прямоугольных треуг-ков равны гипотенуза и один из острых углов, то такие треуг-ки равны, то есть ∆АНР = ∆МНС. Из этого следует, что АР = СМ.

5.1. Прямоугольный треугольник window.top.document.title = «5.1. Прямоугольный треугольник»;

Аксиомы 1.4 и 2.1 позволяли приписывать отрезкам и углам числа, равные их мерам, то есть измерять отрезки и углы. До сих пор не было связи между величинами углов и длинами отрезков. С введением треугольников появляется возможность связать величины градусных мер углов треугольника и длин его сторон. Рассмотрим соотношения между сторонами и углами прямоугольного треугольника.

Рисунок 5.1.1.Прямоугольный треугольник

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Пусть угол (BAC) – искомый острый угол. Так, например, для угла BAC (рис. 5.1.1)

Теорема 5.1.

Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

Теорема 5.2.

Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Модель 5.2.
Доказательство теоремы Пифагора

На рисунке 5.1.3 изображен прямоугольный треугольник. BC и AC – его катеты, AB – гипотенуза. По теореме BC2 + AC2 = AB2.

В прямоугольном треугольнике любой из катетов меньше гипотенузы. Косинус любого острого угла меньше единицы.

Пусть – перпендикуляр, опущенный из точки B на прямую a, и A – любая точка этой прямой, отличная от C. Отрезок AB называется наклонной, проведенной из точки B к прямой a. Точка C называется основанием наклонной. Отрезок AC называется проекцией наклонной.

С помощью теоремы Пифагора можно показать, что если к прямой из одной точки проведены перпендикуляр и наклонные, то

любая наклонная больше перпендикуляра,
равные наклонные имеют равные проекции,
из двух наклонных больше та, у которой проекция больше.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. По определению

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Для угла (BAC) прямоугольного треугольника, изображенного на рис. 5.1.1, имеем

Так же как и косинус, синус угла и тангенс угла зависят только от величины угла.

Рисунок 5.1.4

Из данных определений получаем следующие соотношения между углами и сторонами прямоугольного треугольника: если α – острый угол прямоугольного треугольника , то

катет, противолежащий углу α , равен произведению гипотенузы на sin α;
катет, прилежащий к углу α , равен произведению гипотенузы на cos α;
катет, противолежащий углу α , равен произведению второго катета на tg α.

Нахождение расстояния между параллельными прямыми

Итак, нахождение расстояния между параллельными прямыми сводится к нахождению длины перпендикуляра, проведенного из некоторой точки одной из прямых на другую прямую. При этом подбирается метод, позволяющий это расстояние отыскать. Выбор метода зависит от условий конкретной задачи. В некоторых случаях можно использовать теорему Пифагора, в других — признаки равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п. Если же параллельные прямые заданы в прямоугольной системе координат, то расстояние между заданными параллельными прямыми можно вычислить методом координат. На нем и остановимся.

Сформулируем условие задачи.

Пусть на плоскости или в трехмерном пространстве зафиксирована прямоугольная система координат, заданы две параллельные прямые a и b и требуется найти расстояние между этими прямыми.

Решение этой задачи строится на определении расстояния между параллельными прямыми —чтобы найти расстояние между двумя заданными параллельными прямыми нужно:

определить координаты некоторой точки М₁, лежащей на прямой a (или на прямойb);
вычислить расстояние от точки М₁ до прямой b (или a).

С определением координат точки М₁, лежащей на какой-нибудь из заданных параллельных прямых, проблем не возникнет, если, конечно, Вам знакомы основные виды уравнения прямой на плоскости и уравнения прямой в пространстве. Для нахождения расстояния от точки М₁ до нужной из заданных параллельных прямых Вам будет полезна информация из разделанахождение расстояния от точки до прямой.

В частности, если в прямоугольной системе координат Oxy на плоскости прямую a задает общее уравнение прямой вида , а прямую b, параллельную прямой a, — общее уравнение прямой , то расстояние между этими параллельными прямыми можно вычислить по формуле .

Покажем вывод этой формулы.

Возьмем точку , которая лежит на прямой a, тогда координаты точки М₁удовлетворяют уравнению , то есть, справедливо равенство , откуда имеем .

Если , то нормальное уравнение прямой b имеет вид 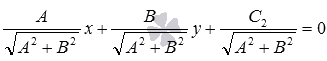, а если , то нормальное уравнение прямой bимеет вид . Тогда при расстояние от точки до прямой b вычисляется по формуле , а при — по формуле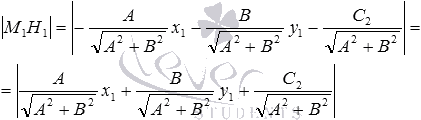

То есть, при любом значении С₂ расстояние от точки до прямой b можно вычислить по формуле . А если учесть равенство , которое было получено выше, то последняя формула примет вид 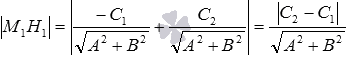. На этом вывод формулы для вычисления расстояние между двумя параллельными прямыми, заданными общими уравнениями прямых вида и завершен.

Разберем решения примеров.

Чему равна сумма двух острых углов прямоугольного треугольника

Для удобства свойства прямоугольных треугольников будут нумероваться наподобие аксиом как $C_x$, где $x$ — номер свойства.

Вновь применим теорему о сумме углов треугольника к прямоугольным треугольникам. Если для всякого такого треугольника известно, что один из его углов равен $90^\circ$, про сумму оставшихся двух углов можно заключить, что они также равняются $90^\circ$. Иными словами, сумма двух острых углов прямоугольного треугольника составляет $90^\circ$.

На примере треугольника $\bigtriangleup{ABC}$:

$$\angle{B}+\angle{C}=90^\circ$$

{"questions":[{"content":"Градусные меры острых углов в прямоугольном треугольнике $\\bigtriangleup{ABD}$ имеют соотношение $2:3$. Чему равняется градусная мера меньшего острого угла? `input-1`","widgets":{"input-1":{"type":"input","unit":"$^\\circ$","answer":"36"}},"step":1,"hints":["Воспользуемся свойством $C_1$:$$2x+3x=90^\\circ$$","Откуда получаем $x=18$.","Находим градусную меру меньшего в паре угла: $$2*18=36^\\circ$$","Ответ: 36."]}]}

Основание равнобедренного прямоугольного треугольника

Применим свойство $C_1$ к треугольнику с равными катетами. Пусть дан такой треугольник, $\bigtriangleup{DBC}$, где $DC=BC$. С одной стороны, $\bigtriangleup{DBC}$ является прямоугольным.

С другой стороны, он соответствует критерию равнобедренного треугольника. Тогда согласно теореме равнобедренного треугольника, заключающей равенство углов при основании, и согласно свойству $C_1$, заключающему, что сумма двух острых углов прямоугольного треугольника равна $90^\circ$, острые углы такого треугольника равны и каждый составляет $45^\circ$:

$$\angle{D}=\angle{B}=45^\circ$$

При этом заметим, что основание равнобедренного прямоугольного треугольника есть гипотенуза. Однако размещение на чертеже такого вида треугольника «гипотенузой к низу» — практика нераспространенная.

Данный чертеж был приведен в пример лишь для того, чтобы визуально выделить основание равнобедренного прямоугольного треугольника.

Определение расстояния от точки до прямой

Определение. Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой.

Расстояние от точки А до прямой b обозначается d(A, b) (читают следующим образом: «Расстояние от точки А до прямой b»).

Например, если в прямоугольном треугольнике ABC угол С прямой, то расстояние от вершины А до прямой ВС равно длине катета АС, а расстояние от вершины В до прямой АС равно длине катета ВС (рис. 121, б). Длина отрезка CF, являющегося высотой этого треугольника, есть расстояние от вершины С до прямой АВ.

Воспользовавшись понятием расстояния от точки до прямой, можно определить понятие расстояния между параллельными прямыми.

Глава VII. Подобные треугольники

§ 1. Определение подобных треугольников

58. Пропорциональные отрезки
59. Определение подобных треугольников
60. Отношение площадей подобных треугольников
Задачи

§ 2. Признаки подобия треугольников

61. Первый признак подобия треугольников
62. Второй признак подобия треугольников
63. Третий признак подобия треугольников
Задачи

§ 3. Применение подобия к доказательству теорем и решению задач

64. Средняя линия треугольника
65. Пропорциональные отрезки в прямоугольном треугольнике
66. Практические приложения подобия треугольников
67. О подобии произвольных фигур
Задачи

§ 4. Соотношения между сторонами и углами прямоугольного треугольника

68. Синус, косинус и тангенс острого угла прямоугольного треугольника
69. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
Задачи
Вопросы для повторения к главе VI
Дополнительные задачи

Практические задания и задачи №№ 121-142

№ 121. □ Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВО = ΔDAO; б) найдите ВС и СО, если CD = 26 см, AD = 15 см.

№ 122. □ На рисунке 53 ∠1 = ∠2, ∠3 = ∠4. а) Докажите, что ΔАВС = ΔCDA; б) найдите АВ и ВС, если АО =19 см, CD = 11 см.

№ 123. □ На биссектрисе угла А взята точка D, а на сторонах этого угла — точки В и С такие, что ∠ADB = ∠ADC. Докажите, что BD = CD.

№ 124. □ По данным рисунка 73 докажите, что ОР = ОТ, ∠P = ∠T.

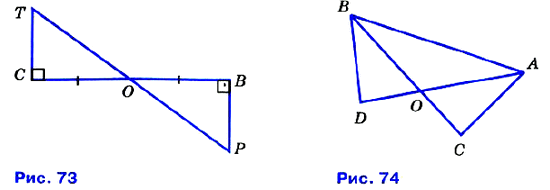
№ 125. □ На рисунке 74 ∠DAC = ∠DBC, АО = ВО. Докажите, что ∠C = ∠D и AC = BD.

№ 126. □ На рисунке 74 ∠DAB = ∠CBA, ∠CAB = ∠DBA, АС =13 см. Найдите BD.

№ 127. В треугольниках АВС и А₁В₁С₁, АВ = А₁В₁, ВС = В₁С₁, ∠B = ∠B₁. На сторонах АВ и A₁B₁, отмечены точки D и D₁ так, что ∠ACD = ∠A₁C₁D₁. Докажите, что ΔBCD = ΔB₁C₁D₁.

№ 128. Докажите, что в равных треугольниках биссектрисы, проведённые к соответственно равным сторонам, равны.

№ 129. Отрезки АС и BD пересекаются в середине О отрезка АС, ∠BCO = ∠DAO. Докажите, что ΔВОА = ΔDOC.

№ 130. В треугольниках АВС и А₁В₁С₁, отрезки СО и С₁О₁ — медианы, BC = B₁C₁, ∠B = ∠B₁ и ∠C = ∠C₁. Докажите, что: а) ΔАСО = ΔА₁С₁О₁; б) ΔВСO = ΔВ₁С₁O₁.

№ 131. В треугольниках DEF и MNP EF = NP, DF = MP и ∠F = ∠P. Биссектрисы углов Е и D пересекаются в точке О, а биссектрисы углов М и N — в точке К. Докажите, что ∠DOE = ∠MKN.

№ 132. Прямая, перпендикулярная к биссектрисе угла А, пересекает стороны угла в точках М и N. Докажите, что треугольник AMN — равнобедренный.

№ 133. Докажите, что если биссектриса треугольника является его высотой, то треугольник — равнобедренный.

№ 134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.

№ 135. Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.

№ 136. □ На рисунке 52 АВ = АС, BD = DC и ∠BAC = 50°. Найдите ∠CAD.

№ 137. На рисунке 53 BC = AD, AB = CD. Докажите, что ∠B = ∠D.

№ 138. На рисунке 75 AB = CD и BD = АС. Докажите, что: a) ∠CAD = ∠ADB; б) ∠BAC = ∠CDB.

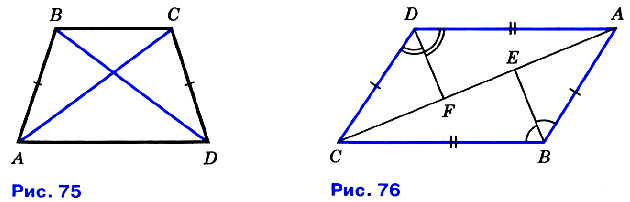
№ 139. На рисунке 76 АВ = CD, AD = BC, BE — биссектриса угла ABC, a DF — биссектриса угла ADC. Докажите, что: а) ∠ABE = ∠ADF; б) ΔАВЕ = ΔCDF.

№ 140. В треугольниках АВС и А₁В₁С₁ медианы ВМ и В₁М₁ равны, АВ = А₁В₁ и АС = А₁С₁. Докажите, что ΔАВС = ΔА₁В₁С₁.

№ 141. В треугольниках АВС и А₁В₁С₁ отрезки AD и A₁D₁ — биссектрисы, АВ = А₁В₁, BD = B₁D₁ и AD = A₁D₁. Докажите, что ΔАВС = ΔА₁В₁С₁.

№ 142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезок CD в точке О. Докажите, что: a) ∠ADB = ∠ACB; б) DO = OC.

Вы смотрели: Практические задания и задачи №№ 121-142 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: (19. Второй признак равенства треугольников. 20. Третий признак равенства треугольников). Геометрия Атанасян Задачи 121-142 + Ответы.

◄ Задачи 100-120 ОГЛАВЛЕНИЕ учебника Задачи 143-155 ►

Пример 1

Пример 1: Задача 272 из учебника «Геометрия 7-9». Автор — Атанасян Л.С.

В равностороннем треугольнике АВС проведена биссектриса АD. Расстояние от точки D до прямой АС равно 6 см. Найти расстояние от точки А до прямой ВС

Рис. 4. Чертёж к примеру 1

Решение:

Равносторонним треугольником называется треугольник с тремя равными сторонами (а значит, и с тремя равными углами, то есть – по 600). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD ⊥BC

Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую АС, то DH – данное расстояние. Рассмотрим треугольник АНD. В нём угол Н = 900, так как DH – перпендикуляр к АС (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла , поэтому AD = (см) (По свойству)

Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD ⊥BC, значит, .

Ответ: 12 см.

Построение треугольника по трём данным его сторонам. Третий признак равенства треугольников

Пусть требуется построить треугольник по трём его сторонам, например, сторона а = 30 мм, сторона с = 40 мм и сторона b = 42 мм. (Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)

Сначала на произвольной прямой построим отрезок АС, равный данному отрезку b, т. е. 42 мм; мы сразу получим две вершины искомого треугольника — А и С.

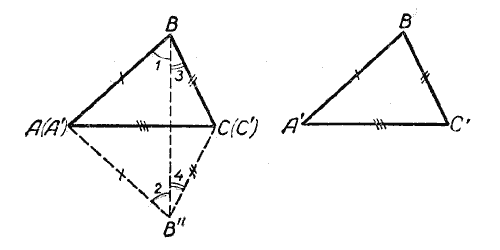
Так как длина второй и третьей сторон соответственно равна отрезкам с и а (в данном случае 40 мм и 30 мм), то третья вершина треугольника должна находиться как на дуге, описанной из центра А радиусом, равным 40 мм, так и на дуге, описанной из центра С радиусом, равным 30 мм. Следовательно, третьей вершиной треугольника будет точка пересечения этих дуг. Обозначив эту точку буквой В и соединив её отрезками с точками А и С, получим искомый треугольник ABC.

По тем же данным построим второй треугольник — Δ А’В’С’ и докажем, что Δ АВС = Δ А’В’С’. Для этого приложим треугольник А’В’С’ к треугольнику ABC так, чтобы их равные стороны А’С’ и AС совместились, причём точка А’ совпала бы с точкой А, точка С — с точкой С. Тогда треугольник А’В’С’ примет положение АВ»С. Сторона АВ будет равна стороне АВ» и сторона ВС — стороне В»С.

Соединив отрезком прямой точки В и В», получим два равнобедренных треугольника ВАВ» и ВСВ», у которых ∠1 = ∠2, а ∠3 = ∠4, откуда ∠B = ∠B». Следовательно, Δ АВС = Δ АВ»С, но тогда и Δ АВС = Δ А’В’С’.

По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.

Мы доказали, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой.

Назовём это третьим признаком равенства треугольников.

Замечания. 1. Во всех трёх признаках равенства треугольников в число трёх данных элементов входит хотя бы одна сторона треугольника.

2. В равных треугольниках против равных сторон лежат равные углы и, обратно, против равных углов лежат равные стороны.

Итак, три признака равенства треугольников:

Виды треугольников

Треугольник остроугольный, если все три угла в треугольнике острые.

Треугольник прямоугольный, если у него один из углов прямой
(=90°).

Треугольник тупоугольный, если у него один из углов тупой.

Примеры:

Основные свойства треугольника:

Против большей стороны лежит больший угол.
Против равных сторон лежат равные углы.
Сумма углов в треугольнике равна
180°.
Если продолжить одну из сторон треугольника, например,
AC,
и взять на продолжении стороны точку
D,
образуется внешний угол
∠BCD
к исходному углу
∠ACB.

Внешний угол равен сумме двух внутренних углов, не смежных с ним.
∠BCD=180°−∠ACB∠BCD=∠A+∠B
Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.

Катет, гипотенуза, угол — обратное свойство

Доказательство

Пусть в прямоугольном треугольнике $\bigtriangleup{ABC}$ катет $AB$ равен половине гипотенузы $BC$:

$$AB=\frac{BC}{2}$$

Докажем, что в таком случае угол $\angle{C}=30^\circ$. То есть докажем, что в случае со свойством $C_2$ также истинным будет и обратное положение. Для этого построим треугольник $\bigtriangleup{ACK}$, равный $\bigtriangleup{ABC}$.

Рассмотрим полученный в результате треугольник $\bigtriangleup{KBC}$. По построению $KC=BC$, $KA=AB$. Заметим, что:

$$BC=2AB=AB+KA=KB$$

Раз $$BC=KB\\BC=KC,$$

то $\bigtriangleup{KBC}$ равносторонний. Отрезок $CA$ в $\bigtriangleup{KBC}$ является высотой и медианой ($KA=AB$). Следовательно $CA$ — биссектриса треугольника в том числе. Тогда $\angle{BCA}=\angle{ACK}$. Поскольку $\angle{BCK}=60^\circ$ (по определению равностороннего треугольника), $\angle{BCA}=\angle{ACK}=30^\circ$.

Угол $\angle{C}$ в прямоугольном треугольнике $\bigtriangleup{ABC}$ равен $30^\circ$. Что и требовалось доказать.

Иными словамиСвойство прямоугольных треугольников, связывающее катет, гипотенузу и угол в $30^\circ$, истинно в «обе стороны». Если про прямоугольный треугольник известно, что в нем есть угол $30^\circ$, катет, лежащий против такого угла, равен половине гипотенузы. С другой стороны, если в прямоугольном треугольнике есть катет, равный половине гипотенузы, то лежащий напротив него угол составляет $30^\circ$. Свойства $C_2$ и $C_3$ являются обратными друг другу.

Общие сведения

Треугольник — замкнутая геометрическая фигура, которая состоит из трёх отрезков, образующих 3 внутренних угла. Другими словами — это многоугольник, состоящий из трёх соединённых точек, не лежащих на одной прямой. При этом их последовательно объединяет 3 линии.

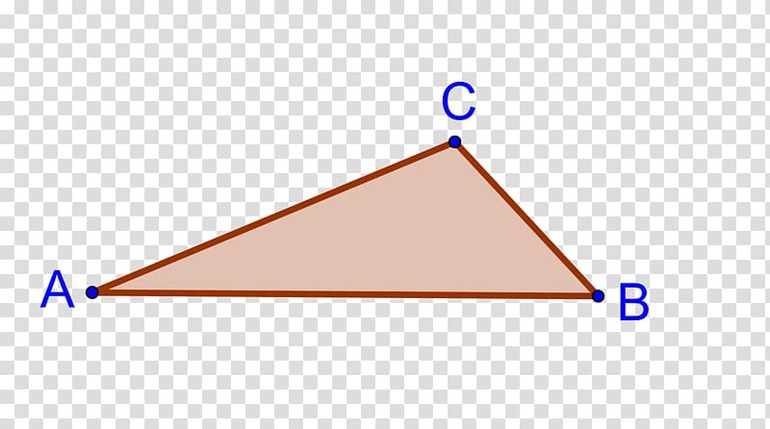
Обозначать фигуру принято тремя латинскими буквами — ABC. Причём по отдельности этими символами подписывают и точки соединения отрезков. Их ещё часто называют вершинами. Углы, которые образуются при них, обозначают одной буквой или используется специальный знак с указанием исходящих из точки линий. Например, в вершине A подписать угол можно как α или ∠ ABC. Стороны, которые лежат против углов, принято указывать маленькими буквами: a, b, c.

Все треугольные многоугольники разделяют на несколько групп по виду их углов. Причём их сумма, вне зависимости от типа фигуры, всегда равна 180 градусов. Треугольники бывают:

остроугольными — все вершины состоят из лучей, градусная мера которых менее 90;
тупоугольными — фигура, у которой хотя бы один из внутренних углов превышает 90;
прямоугольными — один из углов в треугольнике образуется перпендикулярными сторонами.

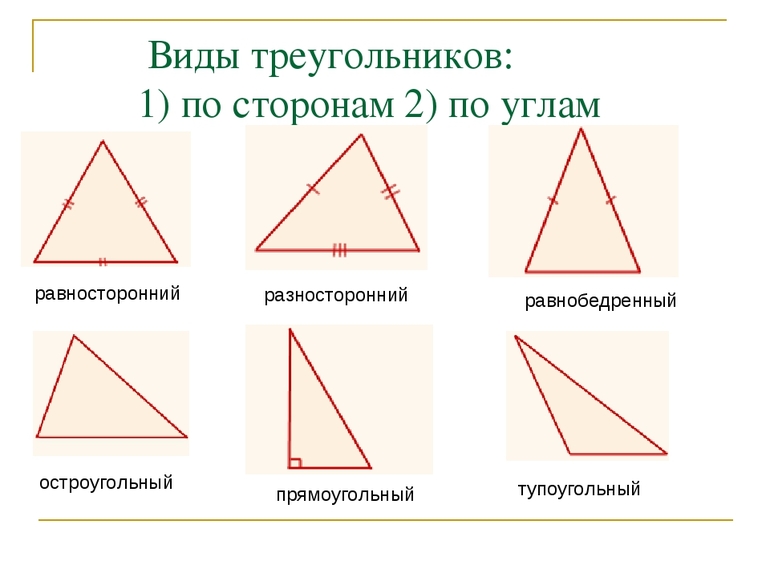
Если у фигуры 2 стороны одинаковы по величине, её называют равнобедренной. Отличный от них отрезок является основанием треугольника. Если же боковые грани в многоугольнике одинаковые, его называют равносторонним или правильным. Есть и третий вид — разносторонний. Все боковые стороны в таком случае не равны друг другу.

Под первой понимают линию, проведённую из угла к противоположной стороне, разделяющей её на 2 одинаковых отрезка. Биссектрисой является прямая, построенная из вершины к противолежащей грани и делящая её пополам. Высота — перпендикуляр, опущенный из вершины на противоположную сторону.

Прямоугольный треугольник с углом в 30°

Особый интерес представляет прямоугольный треуг-к, у которого один из углов равен 30°:

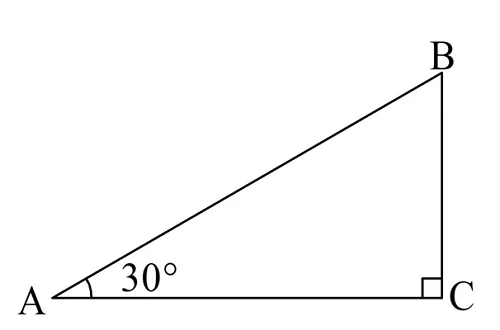
Несложно вычислить его второй угол. Он будет равен 60°:

Оказывается, у данного треуг-ка катет, лежащий против угла в 30° (ВС), вдвое меньше гипотенузы. Докажем это утверждение. Для это приложим к ∆АВС другой, равный ему ∆АСD, получив, по сути, его зеркальное отображение:

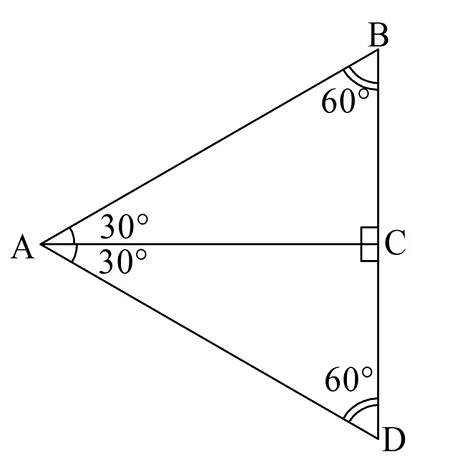
Так как ∠В = 60°, то и ∠D = 60°. Величина угла ∠ВАD равна сумме углов ∠ВАС и ∠САD:

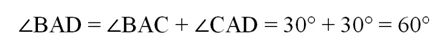
В итоге получается, что в ∆АВD каждый из углов 60°. Это означает, что он является равносторонним, то есть его стороны равны. В частности

Именно это и необходимо было доказать. Аналогично с помощью такого же построения можно доказать обратное утверждение – у прямоугольного треуг-ка, в котором гипотенуза вдвое длиннее одного из катетов, острый угол (тот самый, который лежит против этого катета) равен 30°.

Задание. В треуг-ке СMH угол С – прямой. Внешний угол при вершине M составляет 120°. Известно, что сумма МН и МС составляет 18 см. Чему равны МН и МC?

Решение. Выполним построение треугольника согласно указанным условиям:

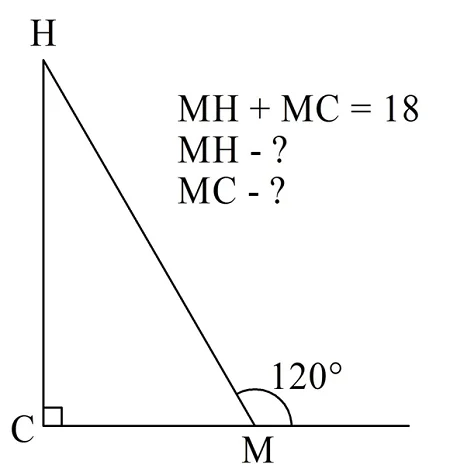
Внешний угол треугольника равен сумме тех 2 углов, которые не смежны с ним. То есть

Итак, рассматриваемый нами треуг-к имеет острый угол, равный 30°. Из этого следует, что катет МС вдвое короче гипотенузы МН:

Задание: У равнобедренного треуг-ка ECB основанием является EC. Известно, что ∠В = 120°. Высота, опущенная из точки Сна боковую сторону ЕВ, равна 9 см. Чему равна длина основания?

Решение.

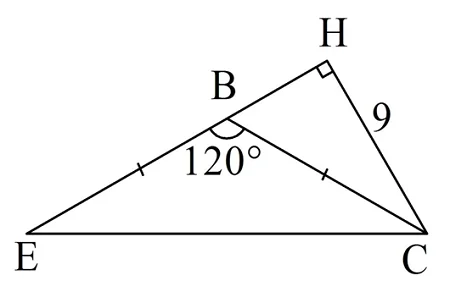
Обозначим высоту как СН

Обратите внимание, что в данном случае высота падает не на сам отрезок ЕВ, а на его продолжение. Эта особенность характерна для всех тупоугольных треуг-ков

Изучим ∆ЕВС. С одной стороны, он равнобедренный. Значит, углы при его основании равны:

Но в сумме все углы треугольника дают 180°. Это позволяет найти углы при его основании:

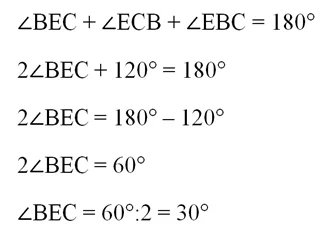
Итак, углы при основании треуг-ка равны 30°. Теперь внимательно посмотрим на другой треуг-к – ЕНС. С одной стороны, он является прямоугольным, ведь ∠ЕНС = 90°. С другой стороны, мы только что вычислили, что один из его острых углов, ∠НЕС, равен 30°. Это значит, что катет НС вдвое должен быть вдвое короче гипотенузы ЕС: