Трапеция. определение, виды, свойства

8. Разные задачи на четырехугольники

При­мер 4. Через дан­ную точку внут­ри угла про­ве­ди­те пря­мую, от­ре­зок ко­то­рой, за­клю­чен­ный внут­ри этого угла, де­лил­ся бы дан­ной точ­кой по­по­лам.

Ре­ше­ние. Внут­ри угла с вер­ши­ной  дана точка . Изоб­ра­зим это на Рис. 20 со всеми эле­мен­та­ми, ко­то­рые по­на­до­бят­ся нам для ре­ше­ния за­да­чи.

Рис. 20

От­ло­жим от­ре­зок  из точки  через точку  так, чтобы , затем про­ве­дем от­рез­ки , по­лу­чим точки пе­ре­се­че­ния со сто­ро­на­ми угла  и  со­от­вет­ствен­но. Со­еди­ним эти точки пря­мой, она и будет ис­ко­мой. До­ка­жем это.

По­стро­ен­ная фи­гу­ра  яв­ля­ет­ся па­рал­ле­ло­грам­мом, т.к. по по­стро­е­нию имеет па­рал­лель­ные про­ти­во­по­лож­ные сто­ро­ны, от­рез­ки  яв­ля­ют­ся диа­го­на­ля­ми па­рал­ле­ло­грам­ма, сле­до­ва­тель­но, по его свой­ству точ­кой пе­ре­се­че­ния () де­лят­ся по­по­лам и , что и тре­бо­ва­лось по усло­вию за­да­чи.

Ответ. Ис­ко­мая пря­мая – .

При­мер 5. В пря­мо­уголь­ни­ке точка пе­ре­се­че­ния диа­го­на­лей от­сто­ит от мень­шей сто­ро­ны на 4 см даль­ше, чем от боль­шей сто­ро­ны. Пе­ри­метр пря­мо­уголь­ни­ка равен 56 см. Най­ди­те сто­ро­ны пря­мо­уголь­ни­ка.

Ре­ше­ние. Изоб­ра­зим Рис. 21.

Рис. 21

Опу­стим из точки пе­ре­се­че­ния диа­го­на­лей пер­пен­ди­ку­ля­ры на сто­ро­ны, длины ко­то­рых и будут рас­сто­я­ни­я­ми от точки пе­ре­се­че­ния диа­го­на­лей до сто­рон пря­мо­уголь­ни­ка. Обо­зна­чим от­ре­зок , тогда по усло­вию . По­сколь­ку  по­лу­ча­ем, что . Под­ста­вим это в фор­му­лу пе­ри­мет­ра пря­мо­уголь­ни­ка:

.

Ответ: .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/povtorenie-teorii-i-reshenie-zadach

https://www.youtube.com/watch?v=axMe7L_01j0

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/83-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/84-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-2.html

http://festival.1september.ru/articles/416997/

Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно). Рассмотрим более подробно некоторые виды выпуклых четырехугольников

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Шаги

1
По известным боковым сторонам и основаниям

1. 1 Запишите формулу для вычисления периметра трапеции. Формула: P = T + B + L + R
2. 2 В формулу подставьте известные длины сторон. Не используйте этот метод, если не даны значения всех четырех сторон.
   • Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид: P = 2 + 3 + 1 + 1
     3 Сложите длины сторон. Так вы найдете периметр трапеции.
     • В нашем примере: P = 2 + 3 + 1 + 1
       

       2
       По известным высоте, боковым сторонам и верхнему основанию

       1. 2 Обозначьте каждую высоту.
       2. 3
          Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны. Не используйте этот метод, если не дано значение верхнего основания.
       3. 4
          Формула: a 2 + b 2 = c 2
       4. 5
          Боковую сторону трапеции подставьте вместо c
          6 Возведите в квадрат известные значения. Затем при помощи вычитания обособьте переменную b
          7 Извлеките квадратный корень, чтобы найти b .) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.
       5. В нашем примере: b 2 = 45
          8 Найдите неизвестную сторону второго прямоугольного треугольника. Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны, то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого.
       6. Например, если вторая боковая сторона трапеции равна 7 см, то формула запишется так: a 2 + b 2 = c 2
          9
          Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R

          3
          По известным высоте, основаниям и нижним углам

       7. 1 Разбейте трапецию на прямоугольник и два прямоугольных треугольника.

          Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.

Для этого из каждой вершины трапеции проведите высоту.

2 Обозначьте каждую высоту.

Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).

Так как высоты являются противоположными сторонами прямоугольника, они равны.

3 Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника).

Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.

Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.

4 Напишите функцию (формулу) синуса угла первого прямоугольного треугольника. Функция: sin ⁡ θ = B H
5 В формулу синуса подставьте известные величины. Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.

• Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так: sin ⁡ (35) = 6 H
  6 Найдите синус угла. Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.
  • При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид: 0 , 5738 = 6 H
    7 Найдите переменную H. Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.
    • В нашем примере: 0 , 5738 = 6 H
      8 Найдите гипотенузу второго прямоугольного треугольника. Напишите функцию (формулу) синуса угла второго прямоугольного треугольника: sin ⁡ θ = B H
      9 Запишите теорему Пифагора для первого прямоугольного треугольника. Формула: a 2 + b 2 = c 2
      10 В формулу подставьте известные величины первого треугольника. Боковую сторону трапеции подставьте вместо c
      11 Найдите b
      12 Найдите основание второго прямоугольного треугольника. Для этого воспользуйтесь теоремой Пифагора (a 2 + b 2 = c 2
      13 Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R или треугольник 90-45-45) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора.
    • Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.
    • Калькулятор
    • Карандаш
    • Бумага

Формулы равнобедренной трапеции

Площадь равняется одной второй произведения высоты геометрической фигуры на полусумму длин оснований.

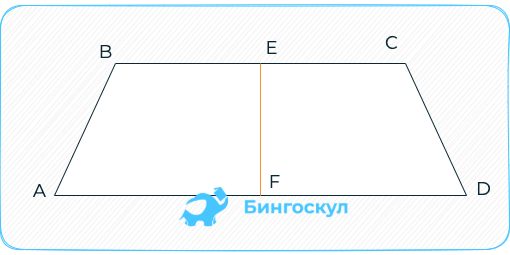
Если высота неизвестна, но есть боковые стороны – c, прибегают к формуле Брахмагупты:

, здесь:

s – половина периметра 4-угольника:

Выражение напоминает упрощённую, благодаря равности боковых сторон, формулу Герона.

Третья формула:

Радиус описанной окружности лежит на оси симметрии, вычисляется по формуле:

 Диагонали вычисляются по указанной ниже формуле.

где:

• h – высота четырёхугольника;
• m – длина средней линии.

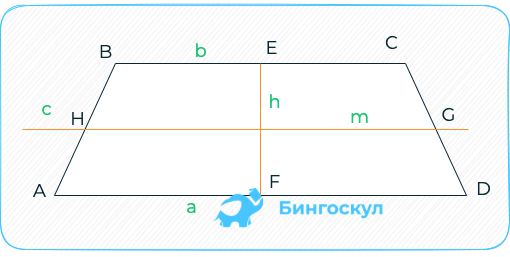
Перпендикуляр OF, проведённый из точки, где пересекаются диагонали, к нижнему основанию, вычисляется по формуле:.

Прямоугольная и равнобедренная трапеция

Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.

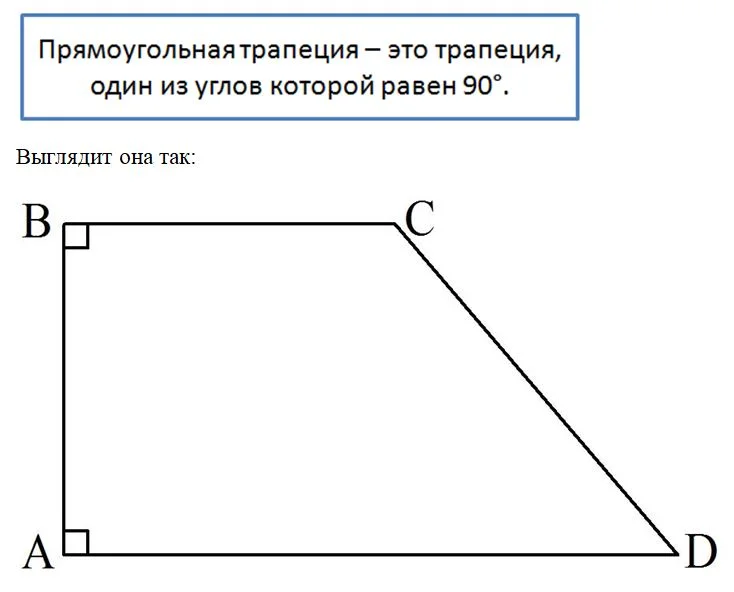
Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия

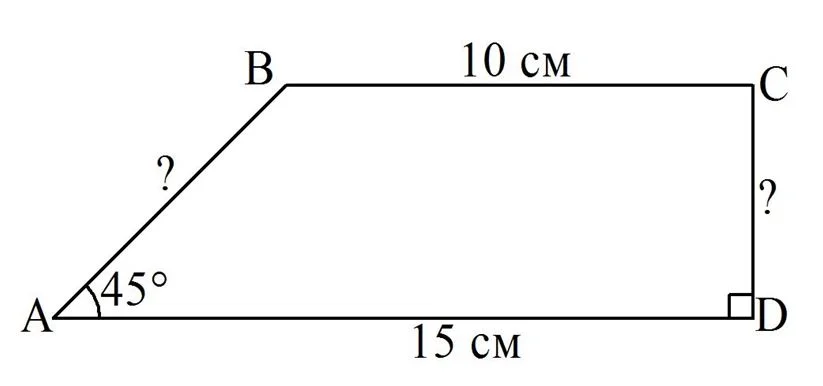
Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?

Решение:

Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:

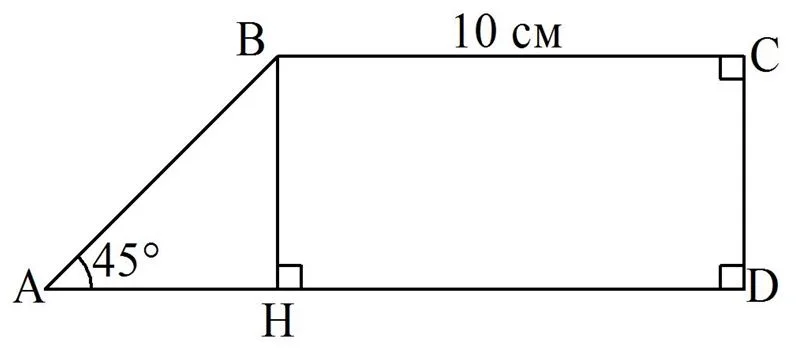
Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:

Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.

Ответ: 5 см.

Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.

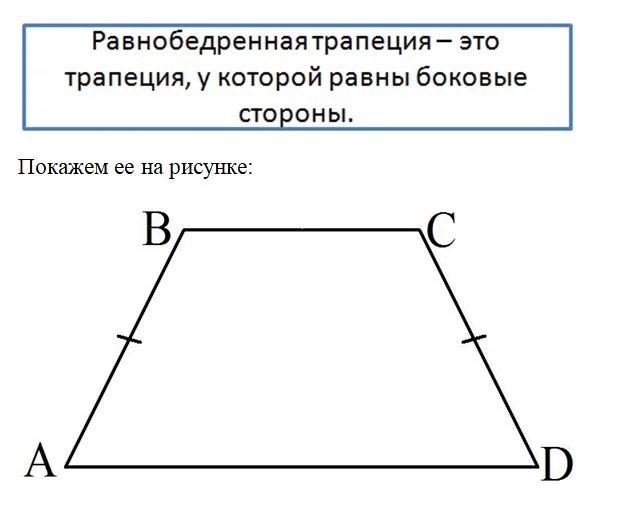
Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.

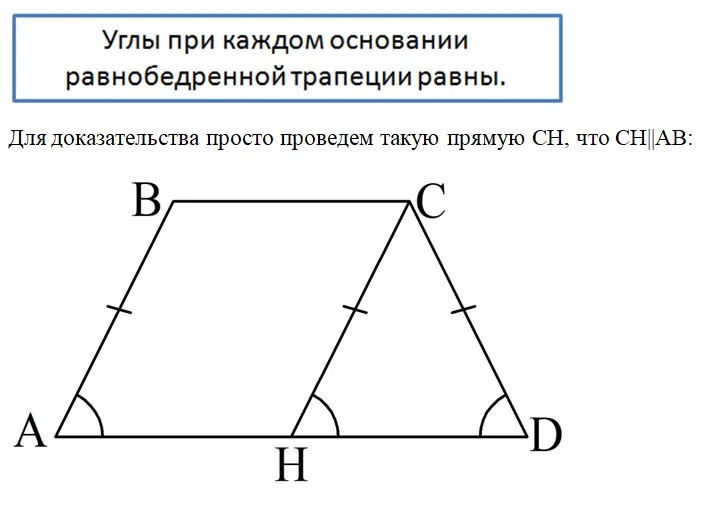
В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда

Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.

Доказывается этот факт с помощью :

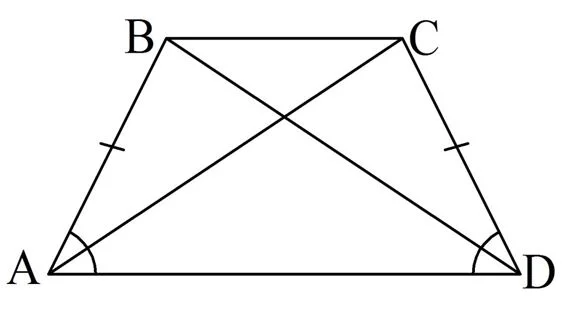
Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь

Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:

Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:

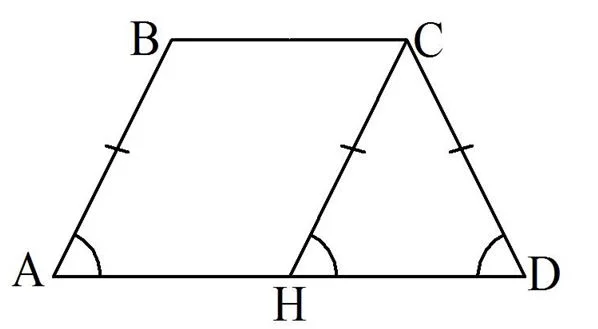
Тогда

Несколько сложнее доказать другую теорему:

Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:

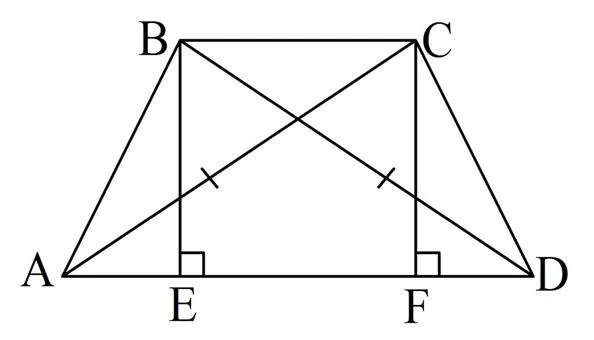
Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что

BE = CF

Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,

Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.

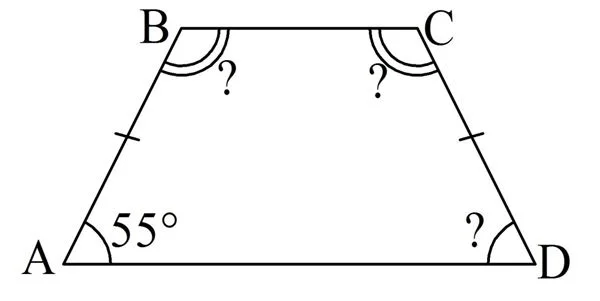
Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:

Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:

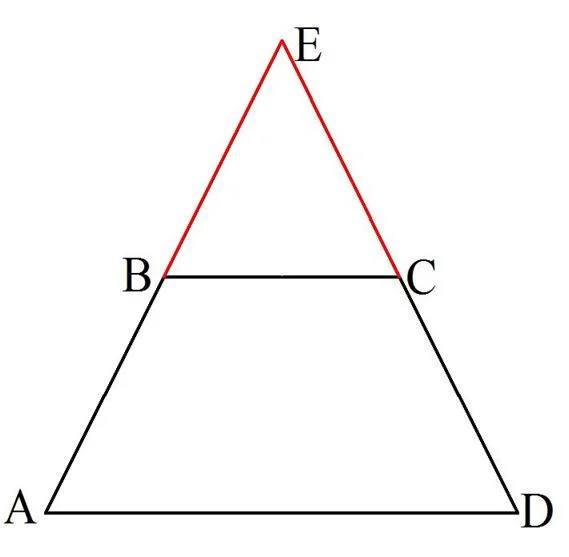
Действительно, если АВСD – равнобедренная трапеция, то

∠А = ∠D

Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.

Свойства равнобокой трапеции

Рассмотрим некоторые важные свойства равнобокой трапеции.

1. В равнобокой трапеции углы при основании равны.

Доказательство:

1) Пусть в трапеции Проведем высоты трапеции и из вершин ее тупых углов и (рис. 70). Получили прямоугольник Поэтому

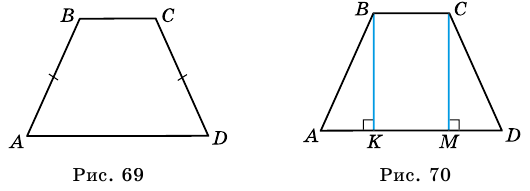
2)  (по катету и гипотенузе). Поэтому

3) Также Но поэтому и Следовательно,

2. Диагонали равнобокой трапеции равны.

Доказательство:

Рассмотрим рисунок 71. (как углы при основании равнобокой трапеции), — общая сторона треугольников и Поэтому (по двум сторонам и углу между ними). Следовательно,

Пример:

 — точка пересечения диагоналей равнобокой трапеции с основаниями и  (рис. 71). Докажите, что

Доказательство:

(доказано выше). Поэтому По признаку равнобедренного треугольника — равнобедренный. Поэтому Поскольку  и то  (так как ). 

Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.

Доказательство:

1) Пусть в  углы при большем основании равны (рис. 70), то есть Проведем высоты и они равны.

2) Тогда (по катету и противолежащему углу). Следовательно, Таким образом, трапеция равнобокая, что и требовалось доказать. 

А еще раньше…

Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).

В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.

Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.

классификация трапеций

Чтобы классифицировать трапецию, мы должны проанализировать ее стороны и углы. Они существуют три возможных случая трапеции, это разносторонняя трапеция, равнобедренная трапеция и прямоугольная трапеция.

прямоугольная трапеция

Трапеция классифицируется как прямоугольник, если у нее есть два углы прямой, то есть два угла, равные 90º.

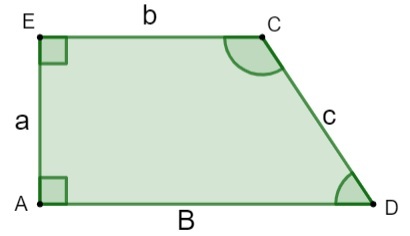
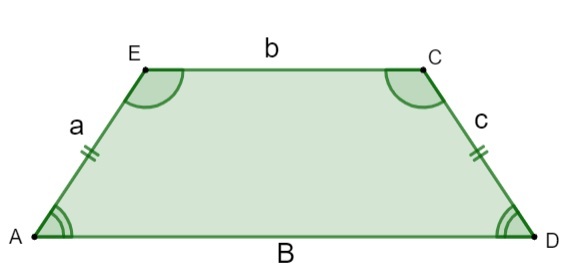
равнобедренная трапеция

Трапеция классифицируется как равнобедренная. когда наклонные стороны совпадают, то есть у них одинаковый размер. Когда это происходит, углы одного и того же основания также совпадают.

Скален Трапеция

Трапеция классифицируется как разносторонняя при не имеет ни одной из конгруэнтных сторон, то есть все стороны имеют разные размеры и, следовательно, все внутренние углы имеют разные размеры.

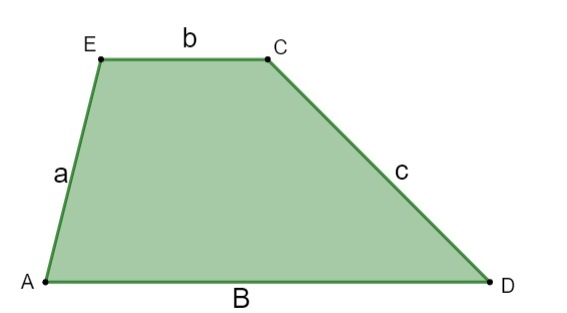
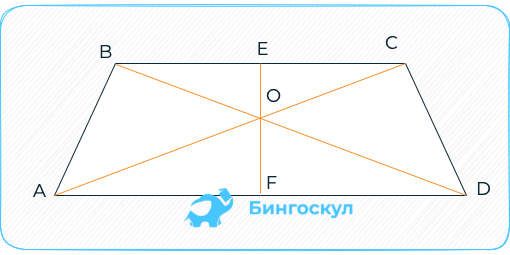
Доказательство теоремы

Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.

Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.

Трапеция

Рассмотрим четырехуг-к, у которого параллельны только две стороны, а две оставшиеся  не параллельны. Такая фигура именуется трапецией.

На рисунке трапеция выглядит следующим образом:

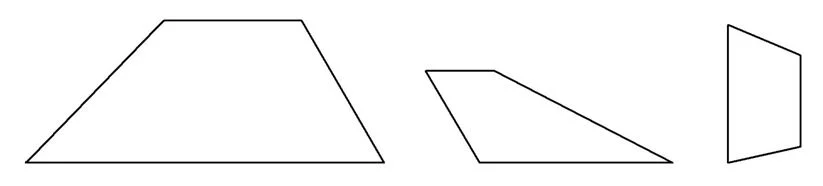
Параллельные стороны именуются основаниями трапеции, а другие две – это боковые стороны.

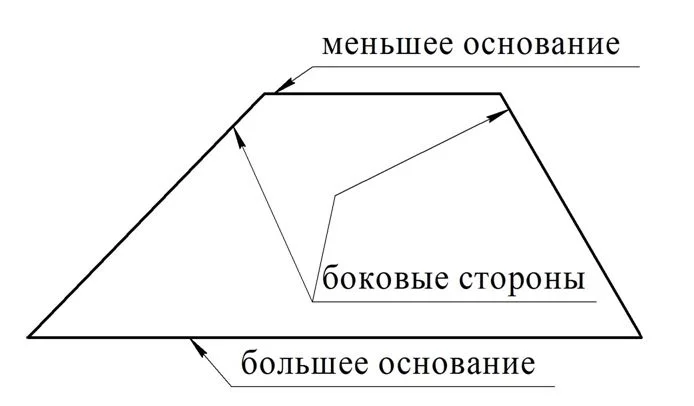
Обратите особое внимание на то, что одно из оснований всегда больше второго основания. Действительно, если бы основания имели одинаковую длину, то получился бы четырехуг-к, у которого две противоположные стороны и равны, и параллельны

Однако это уже один из признаков параллелограмма, а параллелограмм никак не может быть трапецией.

Иногда полезно представлять трапецию как усеченный треуг-к. Действительно, если в треугольнике провести линию, параллельную одной из сторон и пересекающую две остальные стороны, то она как бы «отсечет» верхушку этого треуг-ка, и получится трапеция. И наоборот, любую заданную трапецию можно достроить до треугольника:

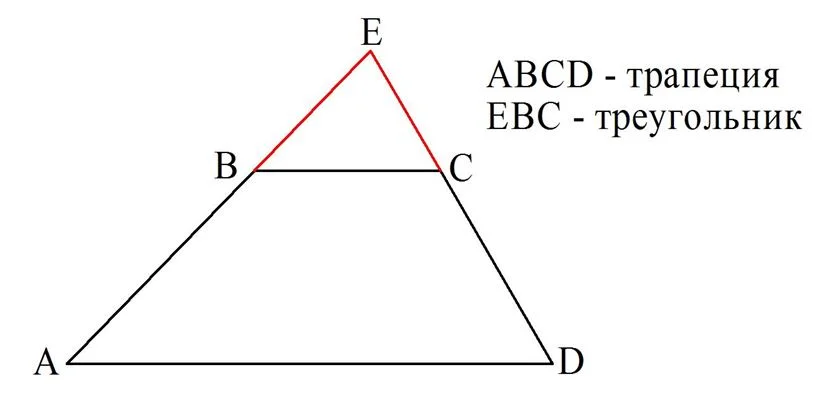
Сумма всех 4 углов трапеции составляет, как и у любого четырехугольника, 360°.

Задание. Известно, что у трапеции АВСD АD||ВС, ∠А = 36°, ∠С = 117°. Найдите∠В и ∠D.

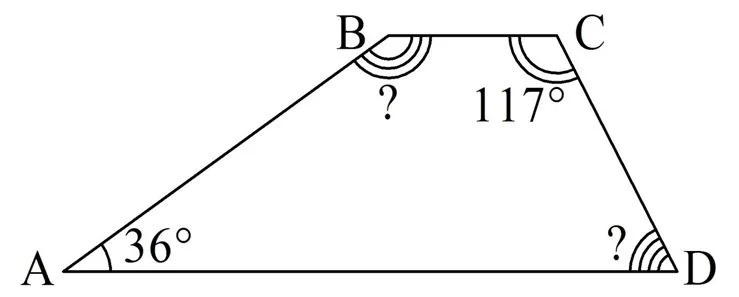
Решение: АВ можно рассматривать как секущую параллельных прямых ВС и АD. Но тогда∠А и ∠В будут являться , а их сумма будет равна 180°. Отсюда можно найти ∠В:

Аналогично, рассматривая в качестве секущей СD, можно найти и ∠D, который вместе с∠С является односторонним:

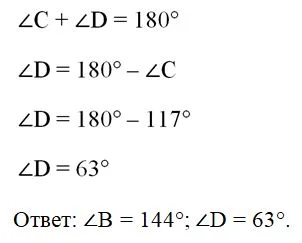
Как найти площадь

Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:

Рисунок 2. Решение задачи на поиск площади

Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что

Пускай DF – будет высотой. Из ΔADE (который будет равнобоким), получим следующее:

Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.

Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.

Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований

Симметрия

В заключение рассмотрим также такое важное геометрическое понятие, как симметрия

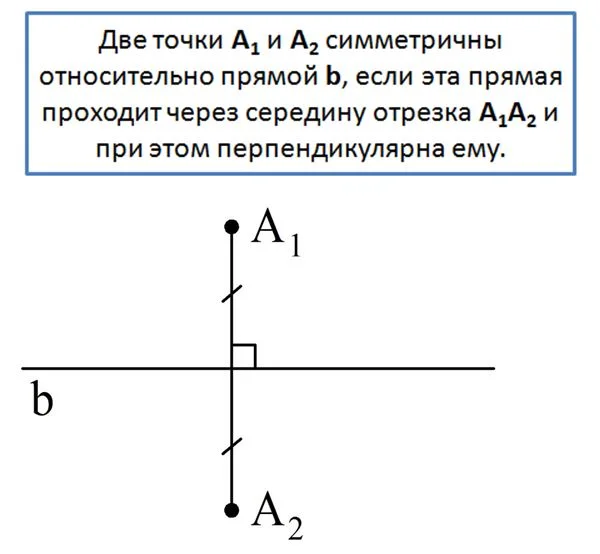
В случае, показанном на рисунке,А₁ и А₂ не лежат на b. Если же рассматривается точка, лежащая на b, то она считается симметричной самой себе. На рисунке пары точек А и B, C и D, M и N симметричны относительно b.Для точки же Р нельзя найти парную ей симметричную точку. Поэтому условно считается, что она симметрична сама себе.

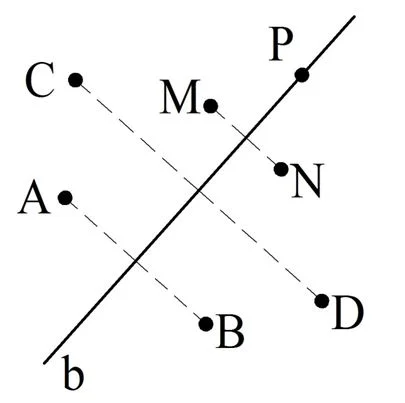
Теперь перейдем к такому понятию, как симметричная фигура.

В качестве иллюстрации приведем равнобедренный треуг-к. У него роль оси симметрии играет медиана, проведенная к основанию. Выберем на треугольнике произвольные точки А₁, В₁, С₁ и D₁. Далее отметим симметричные им относительно b точки, которые обозначим как А₂, В₂, С₂ и D₂. Видно, что они также принадлежат треугольнику:

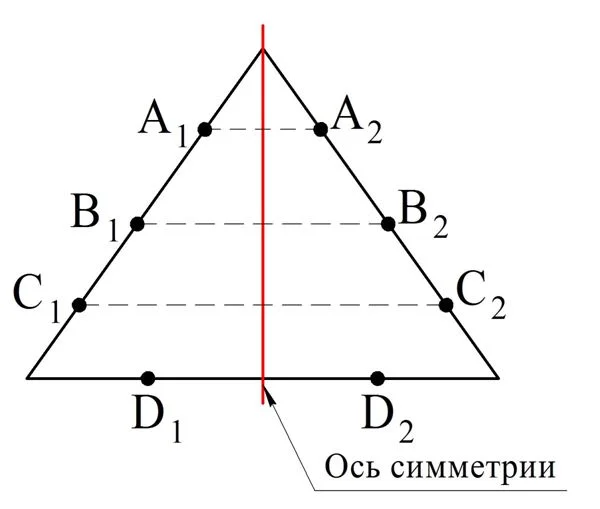
Рассмотрим для иллюстрации и какую-нибудь несимметричную фигуру, например, треугольник с 3 разными сторонами:

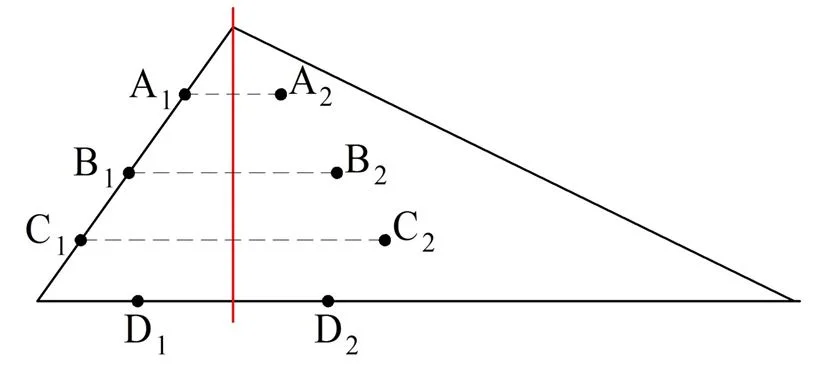
Видно, что например, для точка А₁ симметричная ей А₂ НЕ принадлежит треугольнику, поэтому красная линия НЕ является осью симметрии.

Осевая симметрия присуща и многим другим фигурам:

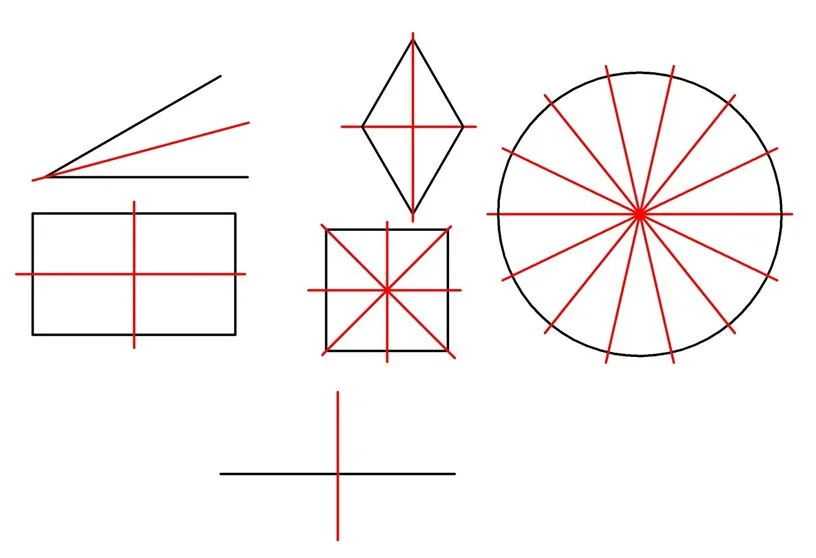
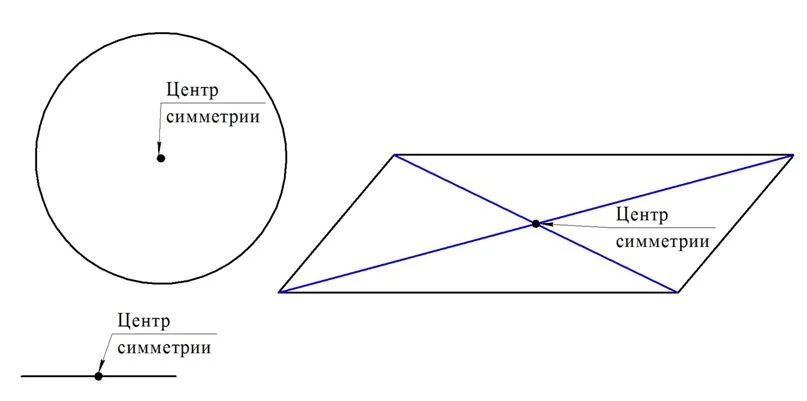
Обратите внимание, что осей симметрии фигуры может быть несколько. У ромба их две (это его диагонали), у квадрата уже четыре (помимо диагоналей добавляются ещё и линии, соединяющие середины его противоположных сторон), а у окружности их и вовсе бесконечно много, так как любой ее диаметр может играть эту роль. Возможен ещё один случай симметрии:

Возможен ещё один случай симметрии:

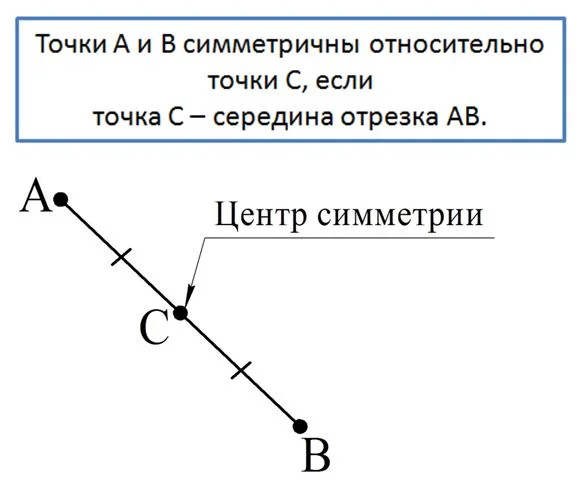
На приведенном рисунке С – это середина АВ, поэтому А и В симметричны, а точка С для них является центром симметрии.

Снова перейдем от отдельных точек к фигурам.

В частности, центральная симметрия присуща параллелограмму (его центром симметрии будет точка, в которой пересекаются его диагонали), а также окружность. Есть центральная симметрия и у любой прямой, причем в качестве центра симметрии фигуры можно выбрать любую точку, принадлежащую этой прямой:

Симметрия – это не просто умозрительная геометрическая конструкция, она встречается и в реальной жизни. Например, листья многих деревьев обладают осевой симметрией, а зубчатое колесо – центральной симметрией. Интересно, что из 32 выделяемых в царстве животных типов у представителей 28 (это более 99% известных видов) можно выделить правую и левую половину, которые симметричны друг другу. Архитекторы и конструктора при проектировании зданий и машин стремятся придать им симметричную форму, так как в большинстве случаев именно такая форма оказывается оптимальной и экономичной.

Свойства

• Сумма углов, прилежащих к боковой стороне трапеции, равна (как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
• Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен среднему гармоническому длин оснований трапеции.
• В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
• Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
• Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
• Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими .
• Если отношение оснований равно , то отношение площадей треугольников, прилежащих к основаниям, равно .
• Высота трапеции определяется формулой:

где  — большее основание,  — меньшее основание, и  — боковые стороны.

Их можно выразить в явном виде:

Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:

а при известных основаниях и диагоналях боковые стороны следующие:

Если же известна высота , то

Прямая Ньютона для трапеции совпадает с её средней линией.

Теорема о четырёх точках трапеции

Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.

Равнобедренная трапеция

Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:

• прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции);
• высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
• углы при любом основании равны;
• сумма противоположных углов равна 180°;
• длины диагоналей равны;
• диагонали трапеции образовывали с одним и тем же основание равные углы;
• из каждой вершины одного основания другое основание было видно под одним и тем же углом;
• вокруг этой трапеции можно описать окружность;
• вершинами этой трапеции также являются вершины некоторого антипараллелограмма.

Кроме того

если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Если — равнобочная трапеция (, ), причём — диагональ трапеции, то .

Вписанная и описанная окружность

• Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
• В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
• Если трапецию можно вписать в окружность — то она равнобедренная.
• Радиус описанной окружности равнобедренной трапеции:[источник не указан 2872 дня]

где  — боковая сторона,  — бо́льшее основание,  — меньшее основание,  — диагонали равнобедренной трапеции.

Если , то в равнобедренную трапецию можно вписать окружность радиуса

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

или

Средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как

Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Формулы площади равнобедренной трапеции

Площадь равнобедренной трапеции:

где  — боковая сторона,  — бо́льшее основание,  — меньшее основание,  — угол между бо́льшим основанием и боковой стороной.

Площадь равнобедренной трапеции через её стороны

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:

В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. .

Этимология и трапеция против трапеции

Ошибка Хаттона в 1795 г.

Древнегреческий математик Евклид определил пять типов четырехугольников, четыре из которых имели два набора параллельных сторон (известные на английском языке как квадрат, прямоугольник, ромб и ромбоид), а последний не имел двух наборов параллельных сторон — τραπέζια ( буквально « трапеция»). стол», сам от τετράς ( tetrás ), «четыре» + πέζα ( péza ), «нога; конец, край, край»).

Два типа трапеций были введены Проклом (412–485 гг. Н.э.) в его комментарии к первой книге « Начал» Евклида :

• одна пара параллельных сторон – трапеция (τραπέζιον), разделенная на равнобедренные (равнобедренные) и разносторонние (неравнобедренные) трапеции
• нет параллельных сторон — трапеция ( τραπεζοειδή , trapezoeidé , буквально трапециевидный ( εἶδος означает «похожий»), точно так же, как кубовидный означает кубический , а ромбовидный означает ромбовидный )

Все европейские языки следуют структуре Прокла, как и английский до конца 18 века, пока влиятельный математический словарь, опубликованный Чарльзом Хаттоном в 1795 году, не поддержал без объяснения перестановку терминов. Эта ошибка была исправлена ​​в британском английском примерно в 1875 году, но сохранилась в американском английском до наших дней.

Тип	Изображение	Оригинальная терминология	Современная терминология
		Евклид (определение 22)	Прокл (Определения 30-34, цитируя Посидония)	Определение Евклида / Прокла	Британский английский (и европейские языки)	Американский английский
Параллелограмм		ῥόμβος (ромбы)	равносторонний, но не прямоугольный	Ромб	Трапецоид ( включительно)
	ῥομβοειδὲς (ромбоиды)	противоположные стороны и углы равны между собой, но не равносторонние и не прямые	Ромбовидный (в просторечии параллелограмм)
Непараллелограмм		τραπέζια (трапеция)	τραπέζιον ἰσοσκελὲς ( трапециевидные изоскелеты )	Две параллельные стороны и линия симметрии	Трапеция _	Трапеция ( эксклюзив )
	τραπέζιον σκαληνὸν ( трапеция ион скалинон)	Две параллельные стороны и отсутствие линии симметрии
	τραπέζοειδὲς ( трапециевидные )	Нет параллельных сторон	Трапецоид _	Трапеция _

В этой статье термин « трапеция » используется в том смысле, который распространен в США и Канаде. Форму часто называют неправильным четырехугольником.

Ромб

Следующая особенная фигура – это ромб. Дадим определение ромба:

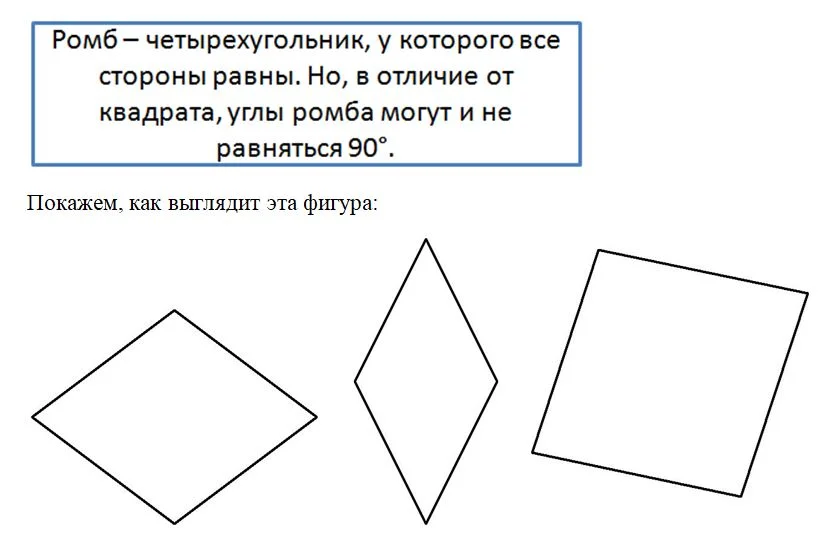
На рисунке видно, что ромб похож на параллелограмм, и это не случайно. Докажем, что любой ромб является частным случаем параллелограмма. Но прежде заметим, что обратное утверждение неверно – отнюдь не каждый параллелограмм является ромбом.

Для доказательства этого факта проведем диагональ ромба:

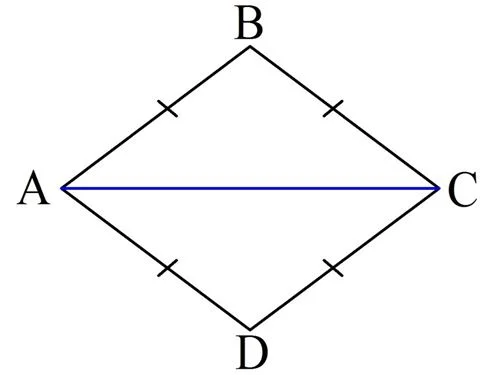
В результате получилось два треуг-ка: ∆АВС и ∆АСD. Можно заметить два факта. Во-первых, каждый из этих треуг-ков – равнобедренный, ведь стороны ромба равны. Тогда можно записать равенство углов:

Из равенства треуг-ков вытекает и равенство углов:

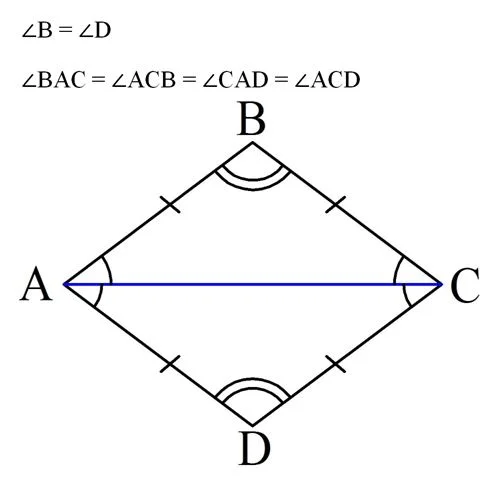
Тогда очевидно, что ∠А и ∠С также равны, ведь они состоят из двух равных углов:

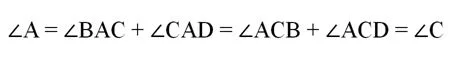
В итоге получается, что в ромбе противоположные углы одинаковы. Зная, что все 4 угла в сумме дают 360°, легко найдем сумму каких-нибудь двух смежных углов:

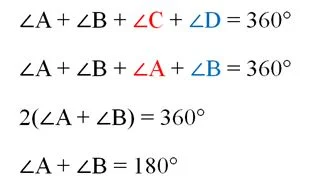
Итак, сумма смежных углов в ромбе равна 180°. Но эти углы можно рассматривать как односторонние. Если их сумма равна 180°, то и соответствующие прямые (в частности, ВС и АD) параллельны. Аналогично доказывается и то, что АВ||CD. Это и значит, что АВСD– параллелограмм.

Продолжим рассматривать построенный нами рисунок, но добавим в него ещё одну диагональ:

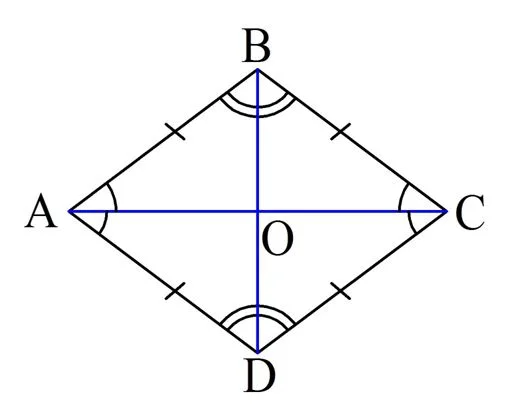
Во-первых, мы уже доказали следующее равенство

Из него вытекает, что диагональ АС является биссектрисой для∠А и ∠С. Аналогично и для диагонали ВD можно показать, что и она разбивает ∠В и ∠D пополам. Можно сформулировать следующее свойство ромба:

Далее рассмотрим ∆АВD. Он равнобедренный, а АО является биссектрисой, падающей на основание ВD. Но в равнобедренном треуг-ке такая биссектриса одновременно является высотой, то есть

Получается, что диагонали всякого ромба обязательно пересекаются под прямым углом.

Задание. Длина стороны ромба совпадает с длиной одной из его диагоналей. Определите углы этого ромба.

Решение. Построим рисунок по условию задачи:

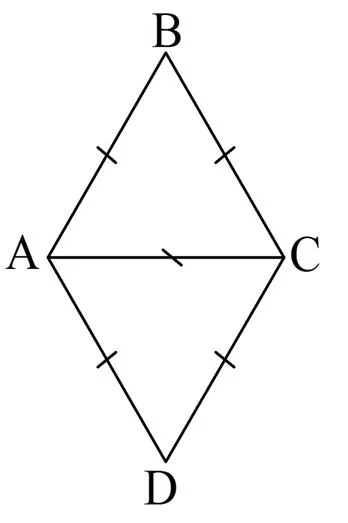
Легко заметить, что∆АВС и ∆АСD будут равносторонними. Однако все углы равностороннего треуг-ка равны 60°:

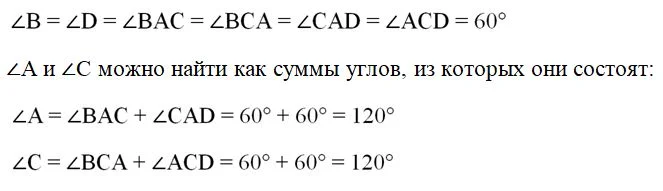
Итак, два угла ромба будут равны 60°, а другие два 120°.

Ответ: 60°; 120°.

Свойства равнобедренной трапеции

• Соединяющий середины параллельных сторон геометрической фигуры отрезок будет центром симметрии трапеции – разделяет четырёхугольник на два одинаковых, отраженных зеркально.
• Опущенный из короткого основания перпендикуляр – высота рассматриваемого многоугольника. Она разделяет нижнее основание на части. Большая равна половине суммы длин оснований, меньшая – их полуразности.
• Вокруг геометрической фигуры описывается круг.

К свойствам диагоналей равнобедренной трапеции относятся:

• Когда диагонали пересекаются под углом 90°, высота геометрической фигуры равняется полусумме параллельных сторон.
• Диагонали одинаковы, пересекаются в точке, принадлежащей оси симметрии.
• Если в рассматриваемый четырёхугольник вписывается окружность, значит, его боковые стороны равны средней линии.
• Площадь 4-угольника с перпендикулярными диагоналями равняется высоте, поднесённой к квадрату.
• Когда в геометрическую фигуру вписывается окружность, её высота равняется корню квадратному произведения оснований.
• Сумма квадратов диагоналей равняется удвоенному произведению протяженностей оснований трапеции плюс сумма квадратов (удвоенному квадрату) боковых сторон.
• Ось симметрии – проведённая между серединами непересекающихся сторон высота.
• Высота, проведённая из верхнего основания, разделяет нижнее на части так: длина большей равняется полусумме оснований, меньшей – половине разности их длин.

Диагонали относятся как:

.

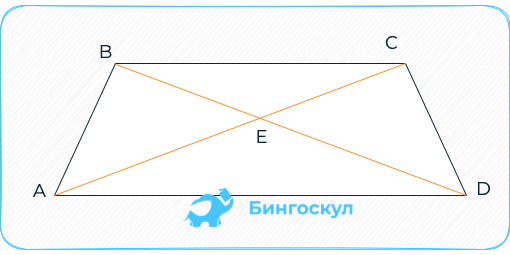
Получается: равнобокая трапеция – это равнодиагональный четырёхугольник.

Известно, что углы при основаниях любой равнобедренной трапеции обладают интересными свойствами:

• перекрёстные углы попарно равны;
• сумма величин лежащих один напротив одного углов составляет 180°;
• углы при нижнем (длинном) основании острые, при верхнем (коротком) – тупые.

Исходя из описанных свойств, существует множество способов расчёта рассматриваемого четырёхугольника.

Определение

Под описание подпадает и параллелограмм с одинаковыми диагоналями. В отличие от него у рассматриваемого 4-угольника боковые стороны не являются параллельными. 

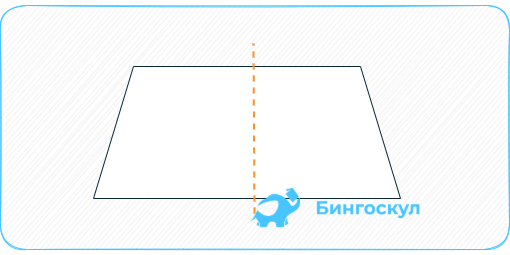
Иногда прямоугольник с квадратом причисляют к частным случаям равнобедренных трапеций, хотя под определение попадают частично.

Встречаются четырёхугольники, называемые трёхсторонними или триравнобедренными – верхняя сторона равная по длине боковым. Их получают посредством сечения четырёх последовательных вершин многоугольника минимум с пятью сторонами. 

Основаниями четырёхугольника называют параллельные стороны, непараллельные – боковыми. Перпендикуляр, проводимый между параллельными сторонами, зовётся высотой геометрической фигуры; отрезок, что соединяет центры боковых сторон, именуют средней линией. Последняя разделяет геометрическую фигуру на две подобные. 

Где еще присутствует трапеция

Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.

Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.

Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции — это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.

На рисунке изображена воздушная трапеция, которую изобрел для цирковых акробатов артист Джулиус Леотард еще в девятнадцатом веке во Франции. Вначале создатель этого номера устанавливал свой снаряд на небольшой высоте, но в итоге он был перенесен под самый купол цирка.

Воздушные гимнасты в цирке выполняют трюки перелетов из трапеции на трапецию, исполняют перекрёстные полёты, проделывают в воздухе сальто-мортале.

В конном виде спорта, трапецией называют упражнение для растяжки или потягивание тела лошади, которое очень полезно и приятно для животного. Во время стойки лошади в положении трапеции работает растяжка ног животного или мышц его спины. Это красивое упражнение мы можем наблюдать во время поклона или так называемого «переднего кранча», когда лошадь глубоко прогибается.

Задание: Наведите свои примеры о том, где еще в повседневной жизни можно услышать слова «трапеция»?

Решение

Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.

Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем тупой угол аналогично первому способу.