Планиметрия. треугольники

их разности ( a b + c , a > b – c ; b a + c , b > a – c ; c a + b , c > a – b ).

Признаки равенства
треугольников.

Треугольники равны, если у них
соответственно равны:

a

) 
две стороны и угол между ними;

b

) 
два угла и прилегающая к ним сторона;

c

) 
три стороны.

Признаки равенства прямоугольных треугольников.

Д

ва

прямоугольных

треугольника равны, если
выполняется одно из следующих условий:

1)  равны их катеты;

2)  катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3)  гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу
другого;

4)  катет и прилежащий острый угол одного треугольника равны катету и
прилежащему острому углу другого;

5)  катет и противолежащий острый угол одного треугольника равны катету и

противолежащему
острому углу другого.

Замечательные линии и точки в
треугольнике.

Высота

треугольника — это

перпендикуляр,

опущенный из любой вершины
на противоположную сторону

(

или её продолжение

).

Эта сторона называется

основанием треугольника

.

Три высоты

треугольника

всегда

пересекаются

в одной точке

,
называемой

ортоцентром

треугольника.

Ортоцентр остроугольного
треугольника ( точка

O

,
рис.26 ) расположен внутри треугольника, а

ортоцентр тупоугольного
треугольника ( точка

O

,
рис.27 )

–

снаружи; ортоцентр прямоугольного треугольника совпадает с
вершиной прямого угла.

Медиана

– это

отрезок

,
соединяющий любую вершину треугольника с серединой противоположной стороны.

Три медианы треугольника

(

AD

,

BE

,

CF

,
рис.28 )

пересекаются в
одной точке

O

,
всегда лежащей внутри треугольника

и

являющейся

его

центром тяжести.

Эта точка делит каждую
медиану в отношении 2:1, считая от вершины.

Биссектриса

– это

отрезок биссектрисы

угла

от вершины до

точки

пересечения с противоположной
стороной.

Три биссектрисы треугольника

(

AD

,

BE

,

CF

,
рис.29 )

пересекаются в
одной точке

О, всегда
лежащей внутри треугольника

и

являющейся

центром
вписанного круга

(см. раздел «Вписанные

и описанные многоугольники»).

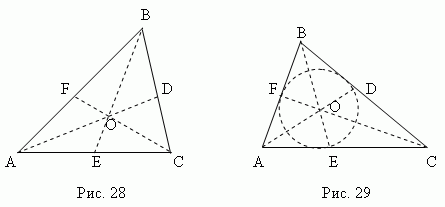
Биссектриса делит противоположную
сторону на части, пропорциональные прилегающим сторонам

;
например, на  рис.29

AE

CE

=

AB

BC

.

Срединный перпендикуляр

– это перпендикуляр,
проведенный из средней

точки

отрезка

(стороны).

Три срединных перпендикуляра
треугольника АВС

(

KO

,

MO

,

NO

,
рис.30

) пересекаются в одной точке О,
являющейся

центром

описанного круга

( точки

K

,

M

,

N

– середины сторон треугольника

ABC

).

В остроугольном треугольнике эта точка
лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном

—

в середине гипотенузы.

Ортоцентр, центр тяжести, центр описанного и
центр вписанного круга

совпадают только в равностороннем
треугольнике.

Теорема Пифагора.

В
прямоугольном треугольнике квадрат длины

гипотенузы равен сумме
квадратов длин катетов.

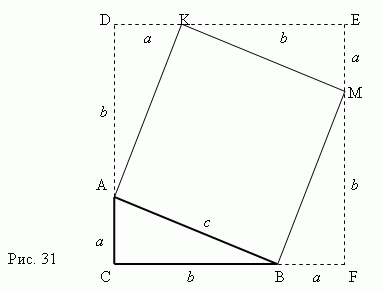
Доказательство теоремы Пифагора с
очевидностью следует из рис.31.

Рассмотрим прямоугольный треугольник

ABC

с катетами

a

,

b

и гипотенузой

c

.

[править] Определения, связанные с треугольником

Окружности

• Вписанная окружность — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.
• Описанная окружность — окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
• Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.

Лучи, отрезки и точки

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.

Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).

Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.

В равнобедренном треугольнике биссектриса, медиана и высота, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Серединные перпендикуляры(медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.

В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера.

Ортоцентр, инцентр, центроид (центр тяжести), а также некоторые другие точки называются замечательными точками треугольника.

Теорема котангенсов

Прочие соотношения

Метрические соотношения в треугольнике приведены для :

•  — формула Эйлера

Где:

• ,  и  — стороны треугольника,
•  — отрезки, на которые биссектриса  делит сторону ,
•  — медианы, проведённые соответственно к сторонам ,  и ,
•  — высоты, опущенные соответственно на стороны ,  и ,
•  — радиус вписанной окружности,
•  — радиус описанной окружности,
•  — полупериметр,
•  — площадь,
•  — расстояние между центрами вписанной и описанной окружностей.
• Для любого треугольника, у которого стороны связаны неравенствами , а площадь равна , длины срединных перпендикуляров или медиатрис, заключенных внутри треугольника, опущенных на соответствующую сторону (отмеченную нижним индексом), равны:

  and 

Радиусы вписанной и описанной окружностей

Следующие формулы включают радиусы описанной R и вписанной r окружностей:

где h_a и т. д. высоты, проведенные к соответствующим сторонам;

и

.

Произведение двух сторон треугольника равно произведению высоте к третьей стороне, умноженной на диаметр описаной окружности.

Площадь треугольника

1. , так как , то:
2.  — формула Герона
3.  ориентированная площадь треугольника.
4.  — 

Частные случаи

1.  — для прямоугольного треугольника
2.  — для равностороннего треугольника

Обозначения

•  — высота, проведённая на сторону ,
•  — полупериметр,
•  — радиус вписанной окружности,
•  — радиус вневписанной окружности, касающейся стороны ,
•  — радиус описанной окружности.

Существуют другие формулы, такие, как например,

для угла α ≠ 90°.

Обозначим через  — радиус вписанной окружности, а через ,  и  — радиусы вневписанных окружностей, касающихся соответственно сторон  и . Тогда имеем

В 1885, Бейкер (Baker) предложил список более ста формул площади треугольника. Он, в частности, включает:

.

Стили нанесения

Современное тату искусство предлагает любителям тату нанести самый простой рисунок в самых разных стилистиках и оттенках, чтобы сделать татуировку максимально индивидуальной и стильной. Треугольник можно набивать в самых распространенных или необычных техниках.

Минимализм

Татуировка в стиле минимализма с треугольником может выглядеть очень стильно и элегантно. Минималистический подход подразумевает использование простых форм и лаконичных линий, что идеально подходит для треугольника. Вот несколько идей для татуировки треугольника в стиле минимализма:

• простой треугольник. Татуировка состоит только из очень простого и четкого треугольника. Она может быть выполнена в черном цвете, чтобы создать более минималистический эффект;
• негативный пространственный треугольник. Татуировка может использовать идею негативного пространства, когда форма треугольника создается пустотой внутри другой фигуры или контура;
• цветной треугольник. Добавьте немного цвета в вашу татуировку треугольника, чтобы она выделялась. Выберите одну яркую цветовую палитру или ограничьтесь монохромными оттенками для более минималистического вида;
• стеклянный (пирамида) или геодезический треугольник. Используйте идею стеклянного или геодезического треугольника, чтобы сделать вашу татуировку более сложной и интересной. Этот дизайн будет обладать уникальным геометрическим видом треугольника.

Важно помнить, что выбор татуировки зависит от вас. Рассмотрите эти идеи и посетите опытного татуировщика, чтобы обсудить вашу конкретную идею и получить рекомендации, учитывающие вашу индивидуальность и ваши предпочтения

Дотворк

Татуировка в стиле дотворк представляет собой композицию, выполненную из множества точек различного размера и плотности. Тату с изображением треугольника в стиле дотворк может выглядеть очень элегантно и стильно. Треугольник может быть выполнен в одной цветовой гамме или сочетать несколько оттенков. Точки разного размера и плотности создают градации и текстуру, делая татуировку уникальной и тонкой визуально. Этот стиль татуировки обычно имеет геометрический наклон, элегантность и абстракцию, а также может быть украшен дополнительными элементами, такими как цветы, линии или геометрический узор. В целом, татуировка треугольника в стиле дотворк подчеркнет индивидуальность и стиль своего обладателя.

Блэкворк

Татуировка треугольника в стиле блэкворк обычно представляет собой треугольник, выполненный в черном или очень темном цвете. Блэкворк — это техника татуировки, которая использует только черные или темные цвета, часто создавая геометрические и абстрактные узоры.

Татуировка треугольника в стиле блэкворк может иметь различные значения в зависимости от контекста и личных предпочтений человека, который её носит. Однако треугольник, как символ, может быть интерпретирован как сила, устойчивость, отсутствие совершенства или просто как декоративный элемент.

Гравюра

Татуировка треугольника в стиле гравюры — это дизайн, в котором треугольник изображается с помощью детализированных и тонких черно-белых линий, напоминающих гравюру. В таком стиле обычно используются резкие углы и точные геометрические формы. Гравюрный стиль подчеркивает контрастность и тонкость изображения, создавая эффект глубины и структуры. Татуировка треугольника в этом стиле может быть символической и иметь личное значение для того, кто ее носит. Она может представлять геометрическую гармонию, баланс или другие абстрактные концепции, а также может быть украшена дополнительными элементами, такими как линии, точки или другие геометрические фигуры.

3Д

Татуировка треугольника в стиле 3D — это дизайн, который придает трехмерный эффект треугольнику на коже. Используя линейные перспективные техники и теневые эффекты, такая татуировка создает иллюзию глубины и объемности. Обычно для этого стиля используются геометрические формы и смешение цветов, чтобы подчеркнуть трехмерный эффект треугольника. Тату с трехмерным треугольником может быть совершенно абстрактной или иметь строгие геометрические линии, в зависимости от предпочтений клиента и творческого подхода татуировщика. Это стильная и современная опция для людей, которые ищут необычный дизайн татуировки.

Точки и линии, связанные с треугольником[править]

Есть сотни различных построений для определения особых точек внутри треугольника, которые удовлетворяют некоторым уникальным условиям. Часто необходимо построить три прямые, связанные аналогично с тремя сторонами (вершинами, углами) треугольника и тогда убедиться, что они пересекаются в одной точке. Важным инструментом для проверки этого является теорема Чевы, которая дает критерии для определения конкурентности прямых. Подобно этому, линии, связанные с треугольником часто строятся после проверки, три аналогичным образом полученные точки является коллинеарными — теорема Менелая дает для этого случая общий критерий. В этом разделе приведены только такие построения, которые наиболее часто встречаются.

Центр описанной окружности.

Срединный перпендикуляр треугольника — это перпендикуляр, который проходит посередине стороны треугольника. Три срединных перпендикуляра пересекаются в одной точке, которая является центром описанной окружности. Диаметр описанной окружности можно определить из теоремы синусов.

Исходя из теоремы Фалеса, можно утверждать, что если центр описанной окружности расположен на одной из сторон треугольника, тогда противоположный угол прямой. Более того, если центр описанной окружности находится внутри треугольника, то треугольник остроугольный, а если наружу, то треугольник тупоугольный.

Три высоты треугольника пересекаются в ортоцентре.

Высота треугольника — прямая, проведенная из вершины и перпендикулярная к противоположной стороне или к продолжению противоположной стороны. Эта сторона называется основанием треугольника. Точка пересечения стороны и перпендикуляра называется основой перпендикуляра. Длина высоты — это расстояние от вершины к основанию треугольника. Три высоты пересекаются в одной точке, которая называется ортоцентром треугольника. Ортоцентр лежит внутри треугольника (и соответственно все основания перпендикуляров лежат в треугольнике) тогда и только тогда, когда треугольник не тупоугольный.

На пересечении двух биссектрис треугольника находится центр вписанной окружности.

Биссектриса треугольника — это прямая, проведенная через вершину, которая делит соответствующий угол на две равные части. Три биссектрисы пересекаются в одной точке, инцентре, центре вписанной в треугольник окружности. Вписанная окружность — это круг, который лежит внутри треугольника и примыкает к трем его сторонам. Кроме того, есть еще три важных круга, внешние вписанные; они лежат за пределами треугольника и соприкасаются с одной его стороной, а также к продолжению других двух. Центры внутреннего и внешних вписанных кругов образуют ортоцентрическую систему.

Барицентр — центр масс треугольника.

Медиана треугольника — это прямая, проведенная через вершину и середину противоположной стороны и делящая треугольник на две одинаковых площади. Три медианы пересекаются в одной точке, которая называется центроидом треугольника. Эта точка также центр масс треугольника: если бы треугольник был сделан из дерева, то можно было бы держать равновесие держась за центроид. Центроид делит каждую медиану в соотношении 2:1, например расстояние между вершиной и центроидом вдвое больше, чем между центроидом и противоположной стороной.

Окружность девяти точек.

Средние точки трех сторон и основы трех высот лежат на одном круге, который называется кругом девяти точек треугольника. Остальные три точки, из-за которых круг получил свое название, это середины той части высоты, лежащей между ортоцентром и вершиной. Радиус окружности девяти точек равен половине описанной окружности. Она соприкасается со вписанной окружностью (в точке Фейербаха) и с тремя внешними вписанными кругами.

[править] Свойства и особенности треугольников

Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.

Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Треугольник, когда не вырожден — всегда выпуклый многоугольник.

Для треугольника всегда существует одна вписанная и одна описанная окружность.

Равенство треугольников

Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?

Нам дано: ∆ABC = ∆A₁B₁C₁. Равны ли соответствующие стороны и углы данных фигур?

По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.

Получается:

Если ∆ABC = ∆A₁B₁C_1, то равны соответствующие стороны:

АС =А₁С₁;

АВ = А₁В₁;

СВ = С₁В₁;

и соответствующие углы равны:

∠С =∠С₁;

∠А = ∠А₁;

∠В = ∠В_1.

Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.

Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.

Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.

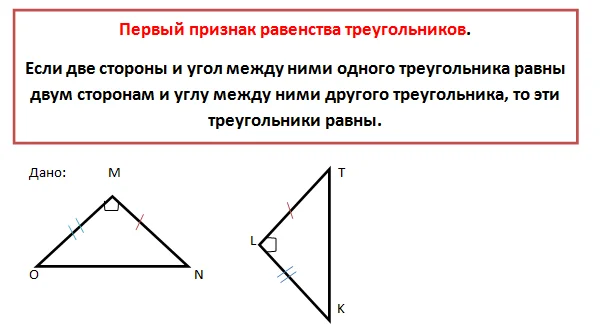
Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.

Значит:

OM=KL, 

MN=LT;

∠M =∠L.

Докажем, что ∆OMN=∆KLT.

Доказательство первого признака равенства треугольников:

Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.

Тогда, сторона OM наложится на сторону  KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.

Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.

Мы доказали, что ∆OMN=∆KLT.

Еще, нам предстоит познакомиться с несколькими понятиями, без которых продолжать изучение  геометрии невозможно.

Начертим прямую АВ. Выберем точку не лежащую на данной прямой. Проведем отрезок СК, соединяющий точку С и прямую АВ, таким образом, чтобы при пересечении СК и АВ образовывался прямой угол (90˚) . Изображенный отрезок СК называют перпендикуляром к прямой.

Доказательство будем проводить в два этапа.

1 этап

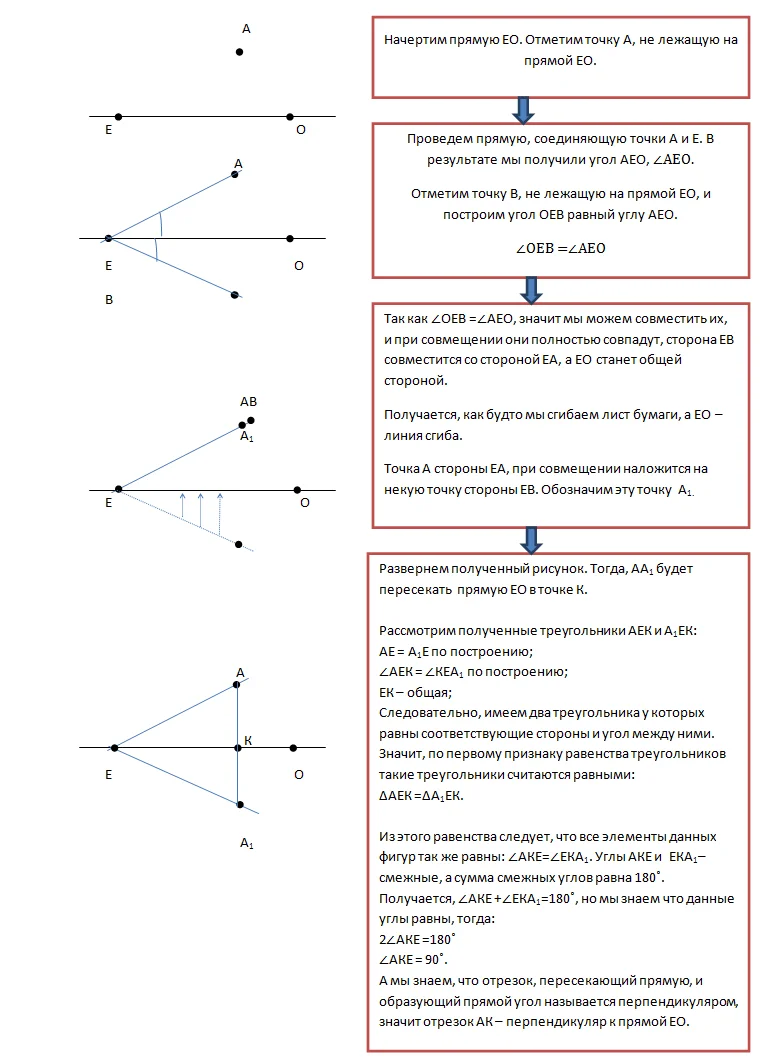2 этап

Теорема доказана.

[править] Типы треугольников

Типы треугольников
Остроугольный	Тупоугольный	Прямоугольный
Разносторонний	Равнобедренный	Равносторонний

По величине углов

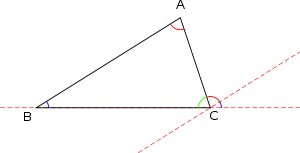
сумма углов треугольника равна 180°.

Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

По числу равных сторон

• Разносторонним называется треугольник, у которого длины трёх сторон различны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Основные линии треугольника

Медиана

Медиана треугольника — это отрезок, соединяющий верщину треугольника
с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую
   из них в отношении 2:1, считая от вершины. Эта точка называется центром
   тяжести треугольника.
3. Весь треугольник разделяется своими медианами на шесть равновеликих
   треугольников.

Биссектриса

Биссектриса
угла — это луч, который исходит из его вершины, проходит между его
сторонами и делит данный угол пополам. Биссектрисой треугольника называется
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на
противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

1. Биссектриса угла — это геометрическое место точек, равноудаленных от
   сторон этого угла.
2. Биссектриса внутреннего угла треугольника делит противолежащую сторону
   на отрезки, пропорциональные прилегажащим сторонам: .
3. Точка пересечения биссектрис треугольника является

Высота

Высотой
треугольника называется перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

1. В высота, проведенная
   из вершины прямого угла, разбивает его на два треугольника,
   исходному.
2. В две его
   высоты отсекают от него треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют
серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов
   этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная
   от концов отрезка, лежит на серединном перпендикуляре к нему.
2. Точка пересечения серединных перпендикуляров, проведенных к сторонам
   треугольника, является центром .

Средняя линия

Средней
линией треугольника называется отрезок, соединяющий середины двух его
сторон.

Окружность, вписанная в треугольник

Окружность, касающаяся всех трех сторон треугольника, называется вписанной окружностью. Только одна окружность может быть вписана в любой треугольник.

Центром пересечения биссектрис, как мы знаем, является инцентром. Инцентром еще называют центром вписанной окружности. Если от инцентрома до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.

Для того, чтобы вписать окружность в треугольник тебе, понадобится циркуль. Выставь циркуль в инцентром и установи радиус равный расстоянию до любого основанию по перпендикуляру. Круговым движением нарисуй окружность.

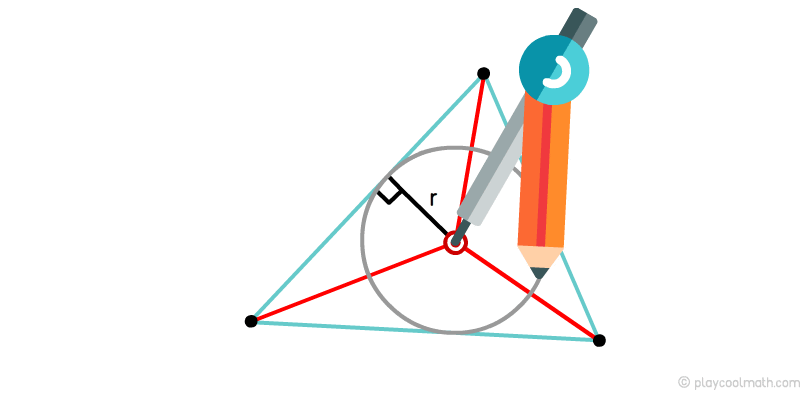
Классификация треугольников по сторонам

Равносторонний треугольник

Равносторонний треугольник или правильный треугольник — это треугольник, у которого все стороны равны. У равностороннего треугольника все углы равны 60°.

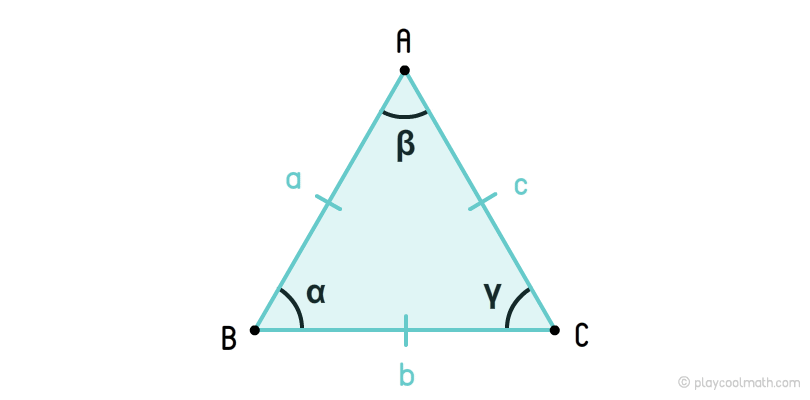
На рисунке мы обозначили стороны как a, b, c, где a = b = c. Углы обозначили как α, β, γ, где α = β = γ = 60°. Одинаковые стороны помечаются одинаковым количеством черточек. Мы пометили стороны a, b, c одной чертой. Одинаковые углы помечаются одинаковым количеством дуг. На рисунке мы все углы пометили одной дугой.

Неравносторонний треугольник

Неравносторонний треугольник — это треугольник, у которого все стороны не равны. У неравностороннего треугольника углы тоже не равны.

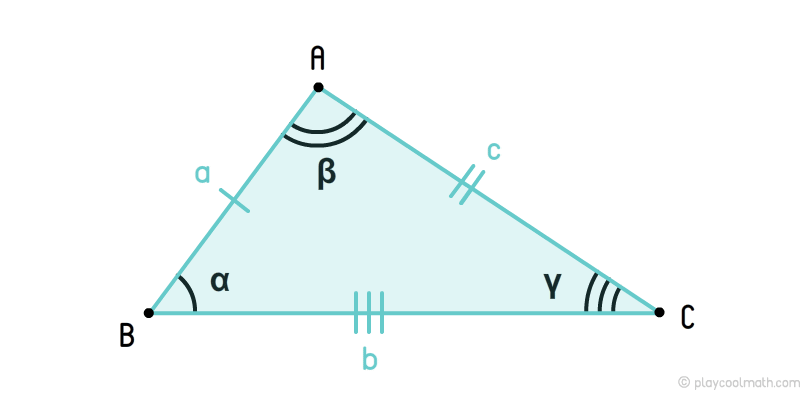
На рисунке мы обозначили стороны a, b, c, где a ≠ b ≠ c. Углы обозначили как α, β, γ, где α ≠ β ≠ γ. Мы пометили стороны a, b, c разным количеством черточек, указав что все стороны имеют разную длину. Все углы пометили разным количеством дуг, указав, что все углы имеют разные угловые меры.

Равнобедренный треугольник

Равнобедренный треугольник — это треугольник, у которого две стороны равны. Эти стороны называются боковыми или бедрами, а третья сторона называется основанием.

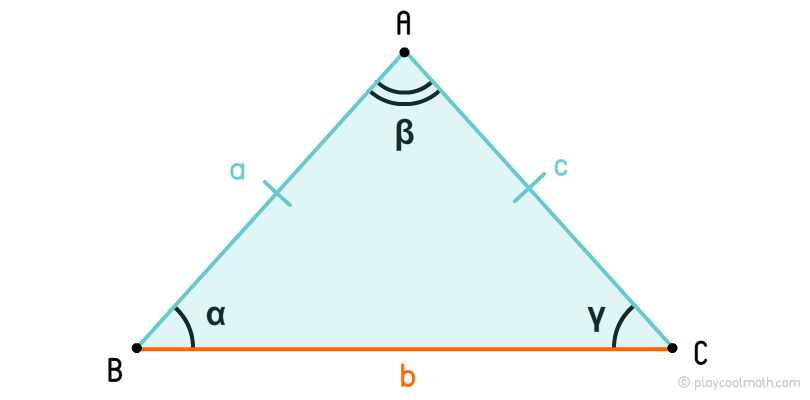
На рисунке мы обозначили боковые стороны как a, c, где a = c, а основание b, где b ≠ a и b ≠ c. У равнобедренного треугольника углы у основания равны α = γ.

Главные типы и виды треугольников

Треугольник — это фигура, образованная тремя отрезками, которые называются сторонами. Существуют различные типы и виды треугольников, включая:

1. Равносторонний треугольник: В этом треугольнике все три стороны и все три угла равны между собой. Углы равностороннего треугольника равны 60 градусам.

2. Равнобедренный треугольник: В этом треугольнике две стороны и два угла равны между собой. Третья сторона и третий угол могут быть различными. Равнобедренный треугольник всегда имеет одну ось симметрии.

3. Прямоугольный треугольник: В этом треугольнике один из углов является прямым (равным 90 градусам). Сторона, противолежащая прямому углу, называется гипотенузой, а остальные две стороны — катетами.

4. Остроугольный треугольник: В этом треугольнике все три угла острые (меньше 90 градусов). Все стороны остроугольного треугольника меньше гипотенузы прямоугольного треугольника, поэтому он более компактный.

5. Тупоугольный треугольник: В этом треугольнике один из углов тупой (больше 90 градусов). Два острых угла меньше 90 градусов.

6. Разносторонний треугольник: В этом треугольнике все три стороны различны по длине. Все три угла также будут различными.

Это лишь некоторые из главных типов и видов треугольников, которые могут встретиться в геометрии.

Тупоугольный треугольник

Следствие 2. В тупоугольном треугольнике один угол тупой, а два остальные угла острые.

Доказательство. В тупоугольном треугольнике NBC (черт. 47) угол NCB тупой. Продолжая сторону NC, мы находим внешний острый угол BCD. Так как BCD > N и BCD > B, то оба угла N и B тупоугольного треугольника острые. Отсюда делаем заключениев треугольнике не может быть более одного прямого и более одного тупого угла.

Теорема 23. Если две стороны одного треугольника равны двум сторонам другого, а углы, заключающиеся между этими сторонам не равны, то против большего угла лежит большая сторона.

Дано. В двух треугольниках ABC и DEF (черт. 48)

AC = DF, AB = DE, угол BAC > угла EDF.

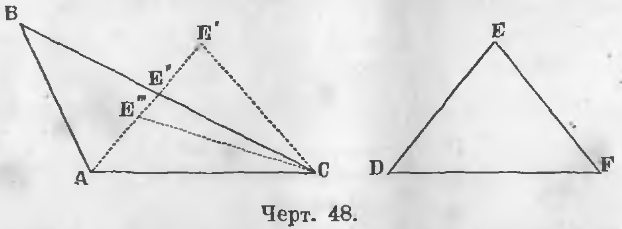
Требуется доказать, что BC > EF.

Доказательство. Наложим треугольник DEF на ABC, стороной DF на AC, точкой D на A. Точка F по равенству сторон DF и AC совпадет с C.

Так как D меньше угла A, то сторона DE пойдет по направлению AE’.

Здесь могут быть три случая: точка E может упасть вне, на сторону и внутри треугольника ABC, т. е. в точках E’, E» и E»’.

1) 1-й случай. Когда точка E упадет в E’, треугольник DEF займет положение треугольника AE’C, следовательно,

AE’ = DE = AB
E’C = EF

Не трудно заметить, что

AE» + E»B > AB
CE» + E»E’ > CE’

Сложив эти неравенства, получим:

AE» + E»B + CE» + E»E’ > AB + CE’

Так как

AE» + E»E = AE’
CE» + E»B = BC

то

AE’ + BC > AB + CE’

Здесь AE’ = AB, следовательно,

BC > CE’ или
BC > EF (ЧТД).

2) 2-й случай. Точка E упадет в E», тогда E»C = EF и

BC > E»C, а следовательно, BC > EF.

3) 3-й случай. Точка E упадет в E»’. В этом случае

AE»’ = DE, E»’C = EF.

По свойству ломаных (теорема 1)

AB + BC > AE»’ + E»’C или
AB + BC > DE + EF.

Так как AB = DE, то последнее неравенство дает

BC > EF

Итак во всех трех случаях BC > EF (ЧТД).

Теорема 24. (Обратная 23). Если две стороны одного треугольника равны двум сторонам другого, а третьи стороны не равны, то против большей стороны лежит больший угол.

Дано. В треугольниках ABC и DEF (черт. 48) AB = DE, AC = DF и BC > EF.

Требуется доказать, что угол BAC > угла EDF.

Доказательство. Здесь могут быть только три предположения: угол BAC может быть равен, меньше или больше угла EDF.

1) Если бы угол BAC равнялся углу EDF, то два треугольника ABC и EDF были бы равны (теорема 20). В этом случае сторона BC равнялась бы стороне EF, что противоречит условию.

2) Если бы угол BAC был меньше угла EDF, то по предыдущей теореме и сторона BC была бы меньше EF, что также противоречит условию; следовательно, угол BAC больше угла EDF (ЧТД).

Свойства треугольников

Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.

Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.

Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.

Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.

Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.

Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.

Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.

Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.

Следующие две теоремы рассматривают свойства для равнобедренных треугольников.

Углы при основании равнобедренного треугольника будут равными.

Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.

Замечание 1

Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.