Сокровище геометрии

Примеры на применение теоремы, обратной теореме Пифагора

Рассмотрим примеры на применение доказанной нами теоремы.

Пример 1. Найдите наименьшую высоту треугольника со сторонами 5, 12, 13.

Решение.

Если обратить внимание на длины сторон треугольника, то можно заметить, что они являются пифагоровой тройкой, т.е. выполнено следующее:

Тогда по теореме, обратной теореме Пифагора, мы можем сделать вывод, что этот треугольник является прямоугольным. Изобразим его на Рис. 3.

Рис. 3

Чтобы искать в этом треугольнике какую-нибудь высоту, нам пригодится его площадь, найдем ее как половину произведения катетов: .

По условию задачи необходимо найти наименьшую высоту треугольника, поскольку наименьшая высота опущена на наибольшую сторону, а наибольшей стороной в прямоугольном треугольнике является гипотенуза, то нам необходимо найти высоту, проведенную к гипотенузе. Выразим ее из формулы площади для произвольного треугольника: .

Ответ. .

Пример 2. Найдите площадь четырехугольника , если .

Решение. Изобразим на Рис. 4 указанный четырехугольник.

Рис. 4

Обратим внимание на то, что длины сторон треугольников образуют пифагоровы тройки: , а из этого следует, что прямоугольные по теореме, обратной теореме Пифагора. По третьему свойству площади можем указать, что

По третьему свойству площади можем указать, что .

Вычислим площади этих треугольников с учетом того, что они прямоугольные: . Таким образом, .

Ответ: 114.

ИСТОЧНИК

http://x-uni.com/geometriya/8-klass/video/teorema-obratnaya-teoreme-pifagora

https://www.youtube.com/watch?v=JQQsr4ErE-I

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/98-teoreticheskij-test-po-geometrii-8-klass-tema-ploshchad.html

http://samopodgotovka.com/index.php/matematika/55-testy-po-geometrii/612-test-po-geometrii-8-klass-tema-teorema-pifagora-obratnaya-teorema-pifagora.html

Решение задач с использованием теоремы Пифагора

Для закрепления материала решим следующие задачи на применение теоремы Пифагора.

Задача 1. Используя приведённые ниже данные о длинах сторон прямоугольных треугольников, вычислите длины других сторон.

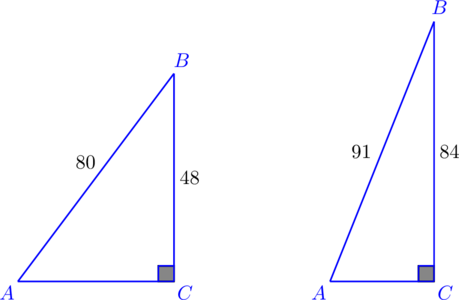
Итак, дано:

Длина одного из катетов равняется 48, гипотенузы – 80.
Длина катета равняется 84, гипотенузы – 91.

Приступим к решению:

a) Подстановка данных в приведённое выше уравнение даёт следующие результаты:

482+ b2 = 802

2304 + b2 = 6400

b2 = 4096

b = 64 или b = -64

Поскольку длина стороны треугольника не может быть выражена отрицательным числом, второй вариант автоматически отбрасывается.

Ответ к первому рисунку: b = 64.

b) Длина катета второго треугольника находится тем же способом:

842+ b2 = 912

7056 + b2 = 8281

b2 = 1225

b = 35 или b = -35

Как и в предыдущем случае, отрицательное решение отбрасывается.

Ответ ко второму рисунку: b = 35

Задача 2. Используя приведённые ниже данные о длинах сторон треугольников, определите, являются ли они прямоугольными.

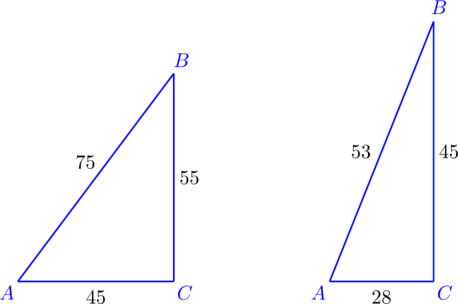
Нам дано:

Длины меньших сторон треугольника равны 45 и 55 соответственно, большей – 75.
Длины меньших сторон треугольника равны 28 и 45 соответственно, большей – 53.

Решаем задачу:

a) Необходимо проверить, равна ли сумма квадратов длин меньших сторон данного треугольника квадрату длины большей:

752= 5625

452+ 552 = 2025 + 3025 = 5050

5625 ≠ 5050

Следовательно, первый треугольник не является прямоугольным.

b) Выполняется та же самая операция:

532= 2809

282+ 452 = 784 + 2025 = 2809

2809 = 2809

Следовательно, второй треугольник является прямоугольным.

Задача 3. Даны точки (-2, -3), (2, 1), (5, -2) в прямоугольной системе координат на плоскости. Выясните, являются ли они вершинами прямоугольного треугольника.

Сперва найдем длину наибольшего отрезка, образованного точками с координатами (-2, -3) и (5, -2). Для этого используем известную формулу для нахождения расстояния между точками в прямоугольной системе координат:

Аналогично находим длину отрезка, заключенного между точками с координатами (-2, -3) и (2, 1):

Наконец, определяем длину отрезка между точками с координатами (2, 1) и (5, -2):

Поскольку имеет место равенство:

то соответствующий треугольник является прямоугольным.

Таким образом, можно сформулировать ответ к задаче: поскольку сумма квадратов сторон с наименьшей длиной равняется квадрату стороны с наибольшей длиной, точки являются вершинами прямоугольного треугольника.

Задача 4. Мальчик Ваня строит ворота. В высоту они должны достигать двух метров, в ширину – трёх. Если допустить, что углы, образованные косяками, окажутся прямыми, то какова будет длина троса, протянутой по диагонали от одного угла к другому?

Основание (расположенное строго горизонтально), косяк (расположенный строго вертикально) и трос (протянутый по диагонали) формируют прямоугольный треугольник, соответственно, для нахождения длины троса может использоваться теорема Пифагора:

Таким образом, длина троса будет составлять приблизительно 3,6 метра.

Задача 5. Мальчику Вите требуется измерить ширину пруда. Он нашёл расстояния от пункта R до пунктов P и Q, расположенных по разным сторонам пруда, как показано на рисунке ниже, и уверился в том, что угол P – прямой. Если допустить, что расчёты верны, какова протяжённость пруда с запада на восток?

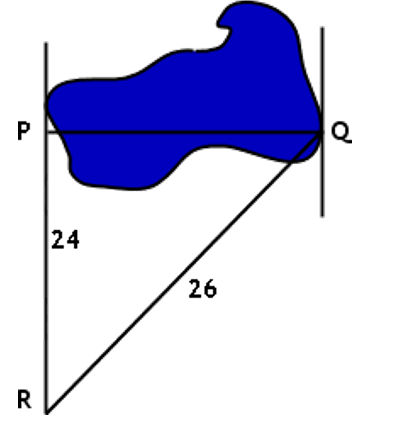
Дано: расстояние от точки R до точки P (катет треугольника) равняется 24, от точки R до точки Q (гипотенуза) – 26.

Итак, помогаем Вите решить задачу. Поскольку стороны треугольника, изображённого на рисунке, предположительно образуют прямоугольный треугольник, для нахождения длины третьей стороны можно использовать теорему Пифагора:

Итак, ширина пруда составляет 10 метров.

Теорема, обратная теореме Пифагора

Для всякой тройки положительных чисел , такой, что , существует прямоугольный треугольник с катетами и гипотенузой .

Доказательство. Рассмотрим треугольник (см. Рис. 1), у которого выполнено такое соотношение сторон: . Докажем, что его угол

Рис. 1

Для того чтобы доказать требуемое утверждение, рассмотрим еще один треугольник , выберем его прямоугольным, т.е. с углом , причем, чтобы было выполнено следующее соотношение с элементами первого треугольника: (см. Рис. 2).

Рис. 2

По теореме Пифагора можем заметить, что для введенного нами второго треугольника выполнено , но из-за указанного равенства сторон между треугольниками: . С другой стороны, по условию , следовательно, .

Таким образом, по трем сторонам, из чего можно сделать вывод, что т.е. треугольник прямоугольный, что и требовалось доказать.

Доказано.

Архив записей

Архив записейВыберите месяц Ноябрь 2022 (1) Сентябрь 2022 (1) Январь 2022 (2) Сентябрь 2021 (1) Июль 2021 (1) Июнь 2021 (2) Май 2021 (1) Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)

Подробное описание действий при доказательстве теоремы

Постараемся доказать, следующее уравнение: a2+b2=c2.

Изобразим прямоугольный треугольник со сторонами a, b, c.

Необходимо прямоугольный треугольник изобразить в виде квадрата.
От катета “а” продолжаем линию вверх на расстояние катета “b”.
Затем проведем линию другого катета “а” вправо.

Получается такой же треугольник, только в перевернутом виде.

Таким же образом изображаем и с другой стороны. Проводим от катета (а) линию катета (b) и опускаем вниз отрезки (а) и (b).

Внизу от катета (b) проводим линию катета (а). В центре фигуры от каждого катета проводим гипотенузы (с).

Таким образом, при помощи построенных гипотенуз получился квадрат в центре фигуры.

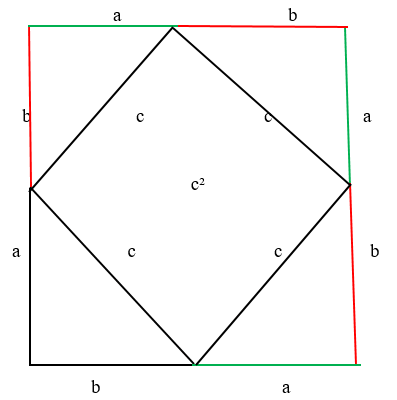
Полученный квадрат состоит из четырех прямоугольных треугольников. Площадь каждого треугольника равняется произведению его катетов.

A именно, \.

Следовательно площадь квадрата в центре равняется квадрату гипотенузе c2, так как все четыре гипотенузы имеют сторону с длиной (с).

Из рисунка видно, что стороны квадрата (четырехугольника) имеют равные значения, следовательно, и прямые углы. Но, нужно доказать, что углы прямые.

Для этого построим квадрат:

Видно, что два обозначенных угла имеет измерение по 90 градусов. Следовательно, если треугольники равны между собой, то и следующие углы так же буду прямыми. То есть равны предыдущим углам.

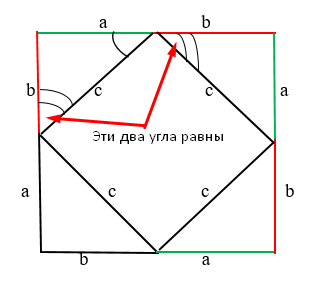
Суммарное значение углов равняется 90 градусов. Следовательно, предыдущий также равен 90 градусов. Таким правилом мы руководствуемся и с другой стороны.

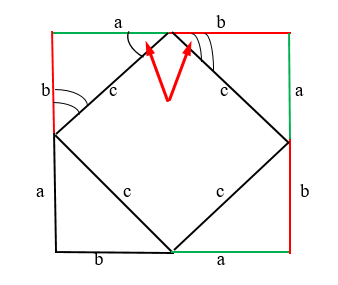
Сумма острых углов в треугольнике, который является прямоугольным равняется 90 градусам. Отсюда следует, что угол квадрата будет равен 90 градусов. Потому что три угла в сумме равняется 180 градусов.

Так как площадь квадрата состоит из: суммы равных площадей, прямоугольных треугольников и площади квадрата. Таким образом, получили фигуру со сторонами a и b.Нам известно, что площадь квадрата со стороной a и b – это будет квадрат его стороны. То есть (a+b)2.

Записываем формулу: (a+b)2;
Далее видим, что площадь прямоугольного треугольника равняется половине произведения его сторон катетов. Составляем выражение: \.
Затем к полученной формуле плюсуем площадь квадрата, который построен в центре фигуры треугольник со стороной. Выполнив перечисленные действия получаем следующее выражение: \
Необходимо опустить скобки: a2+b2+2ab=2ab+c2
Сокращаем уравнение и получаем выражение: c2=a2+b2

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Доказательства теоремы Пифагора.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема

Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие

можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:

доказательства методом площадей
, аксиоматические
и экзотические доказательства
(например,

с помощью дифференциальных уравнений
).

1. Доказательство теоремы Пифагора через подобные треугольники.

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся

напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC
есть прямоугольный треугольник с прямым углом C
. Проведём высоту из C
и обозначим

её основание через H
.

Треугольник ACH
подобен треугольнику AB
C по двум углам. Аналогично, треугольник CBH
подобен ABC
.

Введя обозначения:

получаем:

что соответствует —

Сложив a
2 и b
2 , получаем:

или , что и требовалось доказать.

2. Доказательство теоремы Пифагора методом площадей.

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они

используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость.

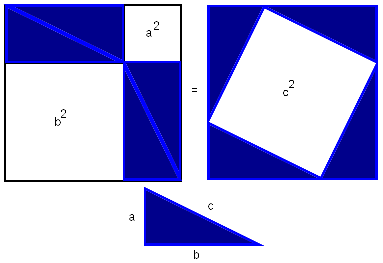Расположим четыре равных прямоугольных

треугольника так, как показано на рисунке

справа.

Четырёхугольник со сторонами c
— квадратом,

так как сумма двух острых углов 90°, а

развёрнутый угол — 180°.

Площадь всей фигуры равна, с одной стороны,

площади квадрата со стороной (a+b
), а с другой стороны, сумме площадей четырёх треугольников и

Что и требовалось доказать.

3. Доказательство теоремы Пифагора методом бесконечно малых.

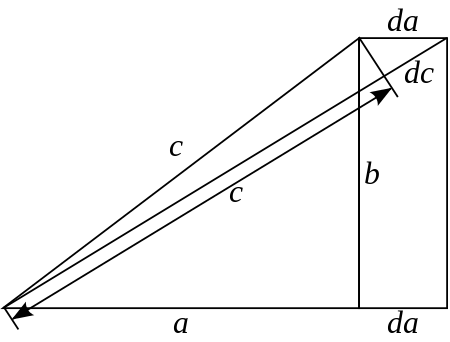
Рассматривая чертёж, показанный на рисунке, и

наблюдая изменение стороны
a
, мы можем

записать следующее соотношение для бесконечно

малых
приращений сторон
с
и
a
(используя подобие

треугольников):

Используя метод разделения переменных, находим:

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:

Интегрируя данное уравнение и используя начальные условия, получаем:

Таким образом, мы приходим к желаемому ответу:

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной

пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми

вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения

(в данном случае катет b
). Тогда для константы интегрирования получим:

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к

в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Примеры решения задач

Пример 1

Задача

Дано: прямоугольный треугольник с катетами 4 и 5.

Найдите гипотенузу. Пока её обозначим “с”

Решение

Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае – .

Воспользуемся теоремой Пифагора:

Итак, , а . Катеты в сумме получают 41.

Тогда . То есть квадрат гипотенузы равен 41.

Квадрат числа 41 = 6,4.

Мы нашли гипотенузу.

Ответ

Гипотенуза = 6,4

Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам.
В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.

Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата, а не в виде кривой, которая обозначает непрямые углы.

Обозначьте стороны треугольника.
Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла).

Определите, какую сторону треугольника требуется найти.
Теорема Пифагора позволяет найти любую сторону прямоугольного треугольника (если известны две другие стороны). Определите, какую сторону (a, b, c) необходимо найти.

Например, дана гипотенуза, равная 5, и дан катет, равный 3. В этом случае необходимо найти второй катет. Мы вернемся к этому примеру позднее.
Если две другие стороны неизвестны, необходимо найти длину одной из неизвестных сторон, чтобы иметь возможность применить теорему Пифагора. Для этого используйте основные тригонометрические функции (если вам дано значение одного из непрямых углов).

Подставьте в формулу a 2 + b 2 = c 2 данные вам значения (или найденные вами значения).
Помните, что a и b — это катеты, а с — гипотенуза.

В нашем примере напишите: 3² + b² = 5²
.

Возведите в квадрат каждую известную сторону.
Или же оставьте степени — вы можете возвести числа в квадрат позже.

В нашем примере напишите: 9 + b² = 25.

Обособьте неизвестную сторону на одной стороне уравнения.
Для этого перенесите известные значения на другую сторону уравнения. Если вы находите гипотенузу, то в теореме Пифагора она уже обособлена на одной стороне уравнения (поэтому делать ничего не нужно).

В нашем примере перенесите 9 на правую сторону уравнения, чтобы обособить неизвестное b². Вы получите b² = 16.

Извлеките квадратный корень из обеих частей уравнения.
На данном этапе на одной стороне уравнения присутствует неизвестное (в квадрате), а на другой стороне — свободный член (число).

В нашем примере b² = 16. Извлеките квадратный корень из обеих частей уравнения и получите b = 4. Таким образом, второй катет равен 4
.

Используйте теорему Пифагора в повседневной жизни, так как ее можно применять в большом числе практических ситуаций.
Для этого научитесь распознавать прямоугольные треугольники в повседневной жизни — в любой ситуации, в которой два предмета (или линии) пересекаются под прямым углом, а третий предмет (или линия) соединяет (по диагонали) верхушки двух первых предметов (или линий), вы можете использовать теорему Пифагора, чтобы найти неизвестную сторону (если две другие стороны известны).

Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
  - a² + b² = c²
  - (5)² + (20)² = c²
  - 25 + 400 = c²
  - 425 = c²
  - с = √425
  - с = 20,6. Таким образом, приблизительная длина лестницы равна 20,6 метров
    .

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются , то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а2, b2 и с2 – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а2 + b2 четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.