Как научиться решать задачи по аналитической геометрии? типовая задача с треугольником на плоскости

7 Формулы приведения

Формулы
приведения позволяют упростить аргумент тригонометрической функции с
целью получения тригонометрической функции угла, при котором
тригонометрическая функция вычисляется, или значительно упрощается.

Если
угол α прибавляется или отнимается от угла, содержащего целое
число значений π, то тригонометрическая функция сохраняется, а
угол упрощается до α. Если угол α прибавляется или
отнимается от угла, содержащего целое число значений π/2, то
тригонометрическая функция меняется на кофункцию (sin-cos,
tg-ctg), а угол
упрощается до α. Принимается знак, который имела бы
первоначальная функция при остром угле α.

Тригонометрическая
функция угла α или выражения с углом α, отложенного на
единичной окружности, соответствует какому-то значению на оси Ox
для функции cos или на оси Oy
для функции sin. Если угол α выбрать
близким к нулю, то отрезок на оси Ox,
равный cosα будет значительно больше
отрезка на оси Oy, равного sinα.
Это позволяет по длине равных отрезков на координатной оси установить
однозначное соответствие между значениями тригонометрических функций
углов 180 — α, 180 + α, 90
— α, 90 + α и тригонометрическими функциями
угла α с учетом знаков на координатных осях.

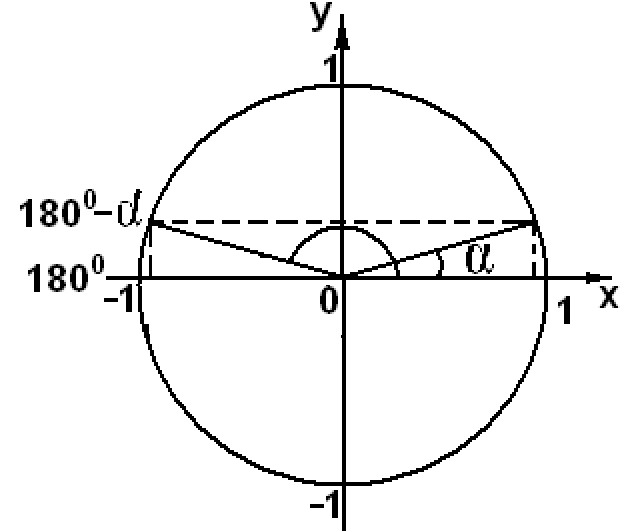
sin(180
— α) = sinα

sin(π
— α) = sinα

cos(180
— α) = — cosα

cos(π
— α) = — cosα

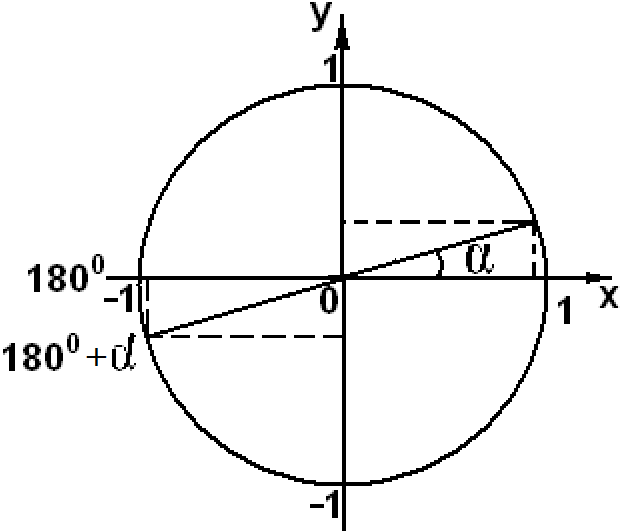
sin(180
+ α) = — sinα

sin(π
+ α) = — sinα

cos(180
+ α) = — cosα

cos(π
+ α) = — cosα

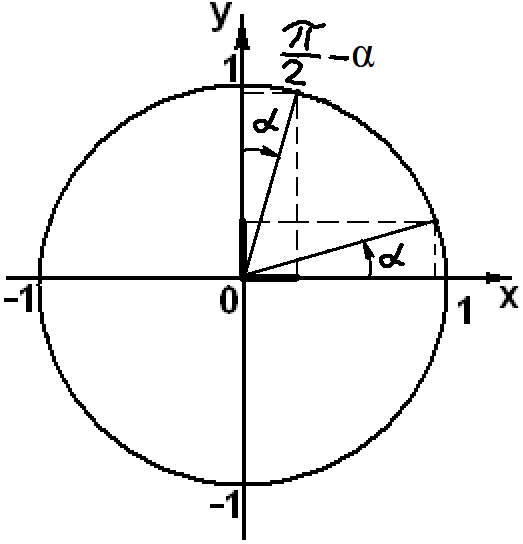
sin(π/2
— α) = cosα

sin(90
— α) = cosα

cos(π/2
— α) = sinα

cos(90
— α) = sinα

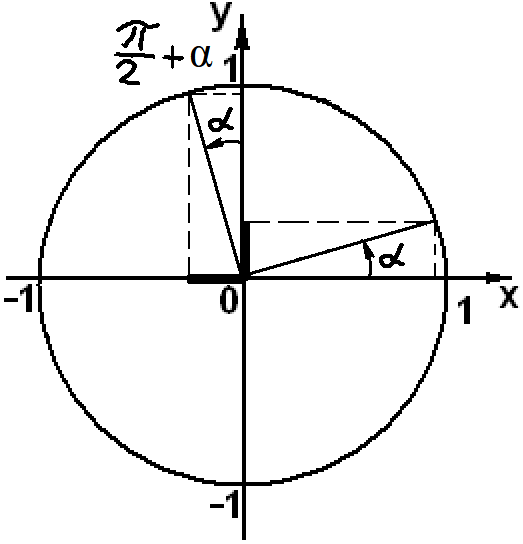
sin(π/2
+ α) = cosα

sin(90
+ α) = cosα

cos(π/2
+ α) = — sinα

cos(90+ α) = — sinα

Определение тригонометрических функций через окружность[]

Пусть на плоскости задана прямоугольная система координат с началом в точке O{\displaystyle O} и с осями OX{\displaystyle {OX}} и OY{\displaystyle {OY}} . Возьмём в этой системе координат окружность с центром в точке O{\displaystyle O} и радиусом, равным единице. Пусть отрезок OA{\displaystyle {OA}} поворачивается на произвольный угол ϑ{\displaystyle \vartheta} вокруг центра O.{\displaystyle O.}

Синусом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают sin⁡ϑ=ACOA.{\displaystyle \sin\vartheta=\frac{AC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то sin⁡ϑ=AC.{\displaystyle \sin\vartheta={AC}.}

Косинусом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают cos⁡ϑ=OCOA.{\displaystyle \cos\vartheta=\frac{OC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то cos⁡ϑ=OC.{\displaystyle \cos\vartheta={OC}.}

Тангенсом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к абсциссе точки A{\displaystyle A}. Обозначают tgϑ=ACOC{\displaystyle \operatorname{tg}\,\vartheta=\frac{AC}{OC}} (в англоязычной литературе tan⁡ϑ).{\displaystyle \tan\vartheta ).} Так как AC=sin⁡ϑ{\displaystyle {AC}=\sin \vartheta} и OC=cos⁡ϑ,{\displaystyle {OC}=\cos\vartheta,} то tgϑ=sin⁡ϑcos⁡ϑ.{\displaystyle \operatorname{tg}\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}.}

Котангенсом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к ординате точки A{\displaystyle A}. Обозначают ctgϑ=OCAC{\displaystyle \operatorname{ctg}\,\vartheta=\frac{OC}{AC}} (в англоязычной литературе cot⁡ϑ).{\displaystyle \cot\vartheta ).} Так как AC=sin⁡ϑ{\displaystyle {AC}=\sin \vartheta} и OC=cos⁡ϑ,{\displaystyle {OC}=\cos\vartheta,} то ctgϑ=cos⁡ϑsin⁡ϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}.} Котангенс равен обратному значению тангенса: ctgϑ=1tgϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{1}{\operatorname{tg}\,\vartheta}.}

Секансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к абсциссе точки A{\displaystyle A}. Обозначают sec⁡ϑ=OAOC.{\displaystyle \sec\vartheta=\frac{OA}{OC}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то sec⁡ϑ=1OC.{\displaystyle \sec\vartheta=\frac{1}{OC}.} Секанс равен обратному значению косинуса: sec⁡ϑ=1cos⁡ϑ.{\displaystyle \sec\vartheta=\frac{1}{\cos\vartheta}.}

Косекансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к ординате точки A{\displaystyle A}. Обозначают cosecϑ=OAAC{\displaystyle \operatorname{cosec}\,\vartheta=\frac{OA}{AC}} (в англоязычной литературе csc⁡ϑ).{\displaystyle \csc \vartheta ).} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то cosecϑ=1AC.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{AC}.} Косеканс равен обратному значению синуса: cosecϑ=1sin⁡ϑ.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{\sin\vartheta}.}

Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.

Урок геометрии и алгебры

Начнём с геометрии. То, что в треугольнике не только три угла, но и три стороны, знает каждый, кто учился в школе. То же самое актуально и для прямоугольного треугольника, только один из его углов равен 90°, огибающие его стороны — катеты, а противоположная и по совместительству самая длинная сторона — гипотенуза.

Два других угла прямоугольного треугольника и являются «точкой отсчёта» для синуса и косинуса. Так, синусом угла является числовое отношение противоположного катета к гипотенузе, а косинусом — смежного катета к гипотенузе. Тангенс же — это отношение противолежащего катета к прилежащему, а котангенс — наоборот.

Для расчёта тригонометрических функций всё это переносится на ось координат. Так косинус (cos) отсчитывается по оси абсцисс (х), а синус (sin) — по оси ординат (y). Для удобства и понимания иногда чертится тригонометрический круг с центром в начале координат и с радиусом, равным единице. На этой окружность откладываются углы.

Тригонометрические тождества

1. $tgα={sinα}/{cosα}$
2. $ctgα={cosα}/{sinα}$
3. $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

$sinα=±√{1-cos^2α}$

$cosα=±√{1-sin^2α}$

4. $tgα·ctgα=1$
5. $1+tg^2α={1}/{cos^2α}$
6. $1+ctg^2α={1}/{sin^2α}$

Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$

Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус

$sin⁡t=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$

Формулы суммы и разности

$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$

$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$

$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$

$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$

Формулы произведения

$cosα·cosβ={cos(α-β)+cos(α+β)}/{2}$

$sinα·sinβ={cos(α-β)-cos(α+β)}/{2}$

$sinα·cosβ={sin(α+β)+sin(α-β)}/{2}$

Формулы сложения

$cos(α+β)=cosα·cosβ-sinα·sinβ$

$cos(α-β)=cosα·cosβ+sinα·sinβ$

$sin(α+β)=sinα·cosβ+cosα·sinβ$

$sin(α-β)=sinα·cosβ-cosα·sinβ$

Вычислить $sin12cos18+cos12sin18$

Данное выражение является синусом суммы

$sin12cos18+cos12sin18= sin⁡(12+18)=sin30=0.5$

Задача (Вписать в ответ число)

Вычислить $sin{5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}$

Решение:

Данное выражение является синусом суммы

$sin {5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}=sin⁡({π}/{12}+{5π}/{12})=sin {6π}/{12}=sin {π}/{2}=1$

Ответ: $1$

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

Решение.

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60   

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два. 
S = 15 √3 / 2

Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Тангенс и котангенс: определение и свойства

Тангенс угла определяется как отношение противолежащей стороны к прилежащей стороне треугольника. Обозначается как tg или tan. Формула для вычисления тангенса: tg(A) = a/b, где A — угол, а a и b — стороны треугольника.

Котангенс угла — это обратное значение тангенса. Он определяется как отношение прилежащей стороны к противолежащей стороне треугольника. Котангенс обозначается как ctg или cot. Формула для вычисления котангенса: ctg(A) = b/a.

Свойства тангенса и котангенса:

• Значение тангенса лежит в диапазоне от минус бесконечности до плюс бесконечности.
• Значение котангенса лежит в диапазоне от минус бесконечности до плюс бесконечности.
• Значение тангенса и котангенса зависит от угла и может быть положительным или отрицательным.
• Значение тангенса и котангенса повторяется с периодом в 180 градусов или π радиан.
• Тангенс и котангенс являются взаимно обратными функциями друг друга.

Тангенс и котангенс широко используются в геометрии, физике, инженерии и других научных дисциплинах для решения задач связанных с треугольниками, углами и прямыми.

Тангенс: определение и свойства

Основные свойства тангенса:

1. Тангенс определяется только для углов в прямоугольном треугольнике.
2. Значение тангенса нельзя выразить через значения синуса и косинуса.
3. Значения тангенса могут быть положительными или отрицательными, в зависимости от квадранта, в котором находится угол.
4. Тангенс угла с нулевым тангенсом равен нулю.
5. Тангенс угла с бесконечным тангенсом не определен.

Тангенс обладает следующими свойствами:

• Тангенс угла равен отношению синуса угла к косинусу угла: .
• Тангенс угла меняет своё значение при переходе через угол, равный 180 градусов или π радиан.
• Периодический характер тангенса: тангенс угла повторяет свои значения с периодом 180 градусов или π радиан.
• Тангенс угла увеличивается от нуля до бесконечности при движении угла от 0 до 90 градусов или от 0 до π/2 радиан.
• Тангенс отрицательного угла равен отрицательному значению тангенса положительного угла такой же меры: .

Котангенс: определение и свойства

Обозначение котангенса угла θ:

Котангенс также может быть определен как отношение косинуса угла к синусу угла:

Свойства котангенса:

1. Значение котангенса всегда отрицательно, кроме точек, где тангенс равен нулю, и известно, что котангенс θ = -cot(θ).
2. Периодичность: котангенс периодичен с периодом π, то есть , где n — целое число.
3. Котангенс угла в прямоугольном треугольнике может быть выражен как отношение длины прилежащего катета к длине противолежащего катета.
4. Котангенс угла отвечает за отношение по горизонтали и вертикали, отрицательное значение обозначает, что две стороны противоположны друг другу.
5. Котангенс функции периодичен с периодом π, что отражается на графике функции.

Тригонометрические функции тупых углов

Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.

Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:

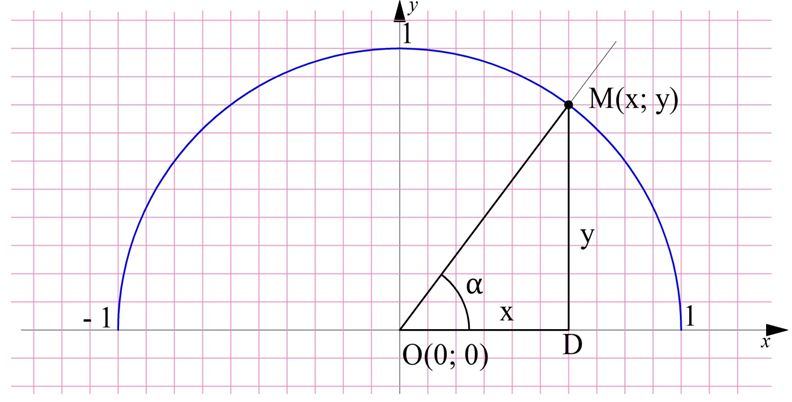
Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:

Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.

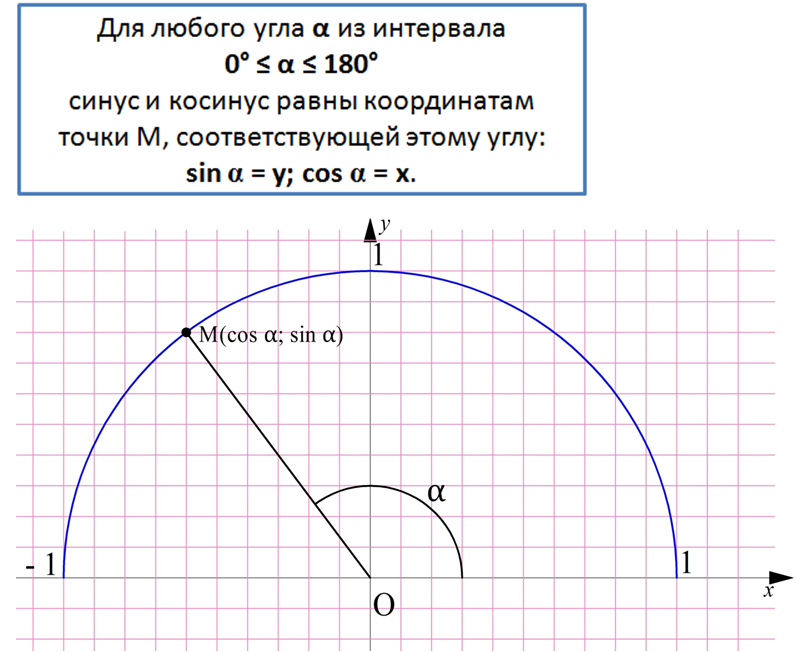
Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.

С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:

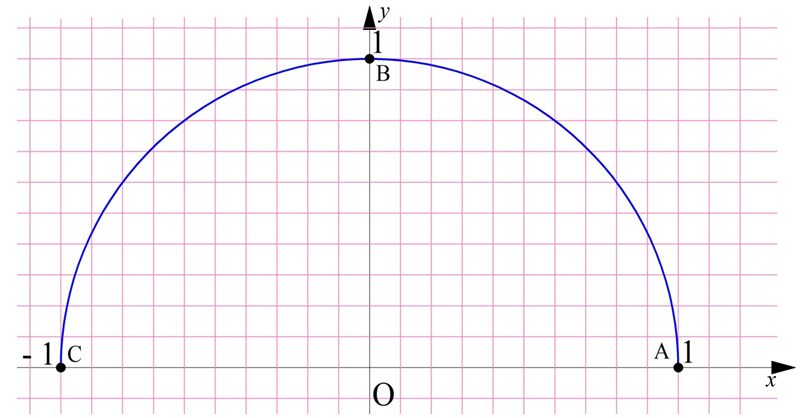
Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:

Используя это определение, найдем тангенс для углов 0° и 180°:

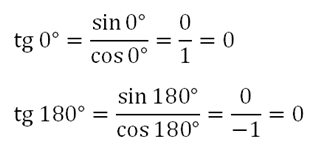
Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.

Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением

Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.

Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:

Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:

Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:

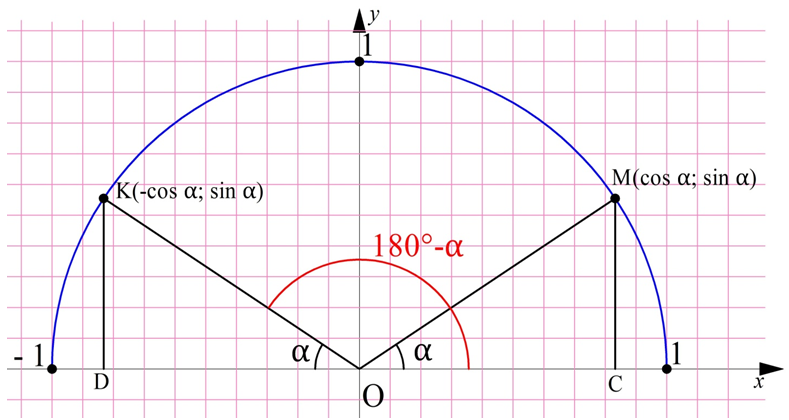
Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как

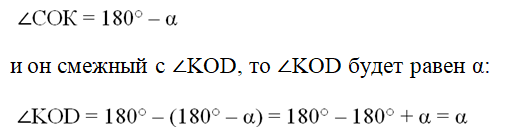
Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому

Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.

Задание. Вычислите sin 150°.

Решение. Представим угол 150° в виде разности:

И всё-таки зачем?

Даже если сейчас вы достаточно взрослый человек, предыдущий пункт может восприниматься не так уж легко, и воспоминания о полученных в школе знаниях не торопятся возвращаться. И вы вполне резонно спросите:  «Вы действительно считаете, что это может пригодиться где-то, кроме уроков геометрии и алгебры?» И мы ответим: «Да, может. Смотрите сами!»

Ближе к звёздамНаших предков тянуло к звёздам не меньше, чем современных людей. И хотя они не летали в космос, они изучали его на уровне, доступном им: они пытались вычислить расстояние до небесных тел. Как они это делали?

Древнейшим астрономическим инструментом считается гномон, представлявший собой вертикальный шест или колонну. В полдень по длине его тени можно было рассчитать угловую высоту солнца. В получении новых знаний использовался котангенс — длина отбрасываемой тени от высоты гномоностолба. Тангенс — непосредственно длина тени.

Этот же способ использовался не только для постижения тайн далёких звезд, но и для определения времени.

Математическое искусствоМатематика кажется нам наукой, не терпящей лирики. И в то же время, искусство невозможно без математики, как и без творческого компонента. Прежде всего, речь идёт о скульптуре и архитектуре. 

Так во время Золотого века искусства людям открылся один парадокс: статуя, выполненная по всем законам композиции, при подъёме на пьедестал стала выглядеть несимметричной, кривой. Оказалось, что скульптор не учёл тот факт, что по правилам перспективы, чем ближе к горизонту, тем меньше смотрится деталь.

Но приблизить фигуру к идеалу помогло знание соотношения тех или иных пропорций. Так, зная расстояние от макушки произведения искусства до человеческого глаза и высоту самой скульптуры, мы можем узнать синус угла падения взгляда. Конечно же, при подъёме статуи на постамент, менялись все величины. Но расчёт коэффициента пропорциональности (из сравнения обычной высоты изваяния с высотой на пьедестале) помог решить эту проблему.

Впрочем, даже если вы не скульптор и не архитектор, это вовсе не значит, что о синусах и косинусах стоит забыть: это важно для построения композиции в живописи и графике, фотографии и даже теории музыки. 

Дела сердечныеНе так давно студентом Иранского факультета были открыты алгебраически-тригонометрические принципы, помогающие всем медикам мира систематизировать знания об электрокардиограмме — главном исследования сердца. Это комплексное математическое равенство, и состоит оно, ни много, ни мало, из 8 выражений, 32 коэффициентов и объединяет 33 основных параметра. Оно настолько продуманное, что включает в себя особые расчёты на случай аритмии. Вот как!

Несколько фактов— Мы не замечаем этого, но наш мозг определяет расстояние до разных окружающих объектов с помощью «встроенной функции» понимания тригонометрических законов;— Движение рыб в воде происходит по законам синуса и косинуса. Для подтверждения можно наметить точку на хвосте и проследить за перемещением. При плавании тельце рыбы принимает форму, сходную с графиком уравнения y=tg x;— В папирусе Ринда (II тысячелетие до н.э.) есть задача. Её условием является нахождение наклона пирамиды с высотой 250 локтей и длиной 360 локтей.

Тригонометрия — это удивительная наука, которая может быть тем или иным образом задействована почти во всех областях человеческой деятельности.Конечно, далеко не каждый из нас становится инженером, астрономом, архитектором или медицинским специалистом. Но, например, создавая уникальный дизайн у себя дома и решив сделать треугольную стойку для цветочного горшка, вы можете вспомнить заветные формулы, и ваш вопрос решится. Впрочем, даже если вы просто любите время от времени поиграть в компьютерные игры, вам стоит знать, что даже их создание не обходится без пресловутых синусов и косинусов. 

Формулы суммы и разности тригонометрических функций

1. Синус суммы и разности:
   $$\mathbf{\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);}$$
   $$\mathbf{\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);}$$
2. Косинус суммы и разности:
   $$\mathbf{\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha);}$$
   $$\mathbf{\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);}$$
3. Тангенс суммы и разности:
   $$\mathbf{tg(\alpha+\beta)=\frac{tg(\alpha)+tg(\beta)}{1-tg(\alpha)*tg(\beta)};}$$
   $$\mathbf{tg(\alpha-\beta)=\frac{tg(\alpha)-tg(\beta)}{1+tg(\alpha)*tg(\beta)};}$$
4. Котангенс суммы и разности:
   $$\mathbf{сtg(\alpha+\beta)=\frac{-1+сtg(\alpha)*ctg(\beta)}{ctg(\alpha)+ctg(\beta)};}$$
   $$\mathbf{сtg(\alpha-\beta)=\frac{-1-сtg(\alpha)*ctg(\beta)}{ctg(\alpha)-ctg(\beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение \(sin(\frac{\pi}{2}+\alpha)\).

Воспользуемся формулой синуса суммы:
$$\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);$$
$$\sin(\frac{\pi}{2}+\alpha)=\sin(\frac{\pi}{2})*\cos(\alpha)+\sin(\alpha)*\cos(\frac{\pi}{2})=$$
$$=1*\cos(\alpha)+\sin(\alpha)*0=\cos(\alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение \(\sin(15^o)=?\)

\(15^o\) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим \(15^o\) в виде разности стандартных углов \(15^o=45^o-30^o\). И воспользуемся формулой синуса разности:
$$\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
$$\sin(15^o)=\sin(45^o-30^o)=\sin(45^o)*\cos(30^o)-\sin(30^o)*\cos(45^o)=$$
$$=\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
Вот мы наши синус \(15^o\). Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: \(\sin(15^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Пример 5
Найдите значение \(\cos(75^o)=?\)

\(75^o\) можно представить в виде суммы стандартных углов \(75^o=30^o+45^o\). Здесь воспользуемся формулой косинуса суммы:
$$\cos(\alpha+\beta)=\cos(30^o)*\cos(45^o)-\sin(30^0)*\sin(45^0)=$$
$$=\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что \(\cos(75^o)=\sin(15^o)\). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: \(\cos(75^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.

11.4 Решение уравнения ctg α = y

Если
необходимо найти угол α при известном y,
то решением уравнения

ctg
α = y

будет

α
= arcctg y + πn,
n ϵ Z.

Задача.
Для заданного

.

Найтиcosα.

Решение

sin2α
+ cos2α
= 1;

cos2α
= 1 — sin2α;

.

Так
как угол принадлежит первой координатной четверти, то косинус этого
угла положительный

Ответ:
cosα
= 0,75.

Пример.
Решите уравнение

и
укажите корни уравнения наотрезке.

Решение

Найдем
корни уравнения на отрезке .

Разделим
на π все части неравенства

-12
≤ ±1+12n ≤ 24

Для
оценки значений n уберем ±1

-12
≤ 12n ≤ 24;

-1
≤ n ≤ 2;

Выражение

при
n = -2 значения
меньше заданного отрезка [-π;
2π

При
n = -1

При
n =

При
n = 1

При
n = 2

Ответ:

.

6
корней уравнения на промежутке :

.

Пример.
Решите уравнение

3sin2x
+
ctg2x
sin2x
— 2
=
0

и
укажите корни уравнения на отрезке

.

Решение

3sin2x
+ cos2x
= 2;

3sin2x+
1 — sin2x=
2;

2sin2x
= 1;

Функция
нечетная: arcsin (-x)
= -arcsin x, поэтому
вынесем ±
за arcsin

Выберем
корни уравнения на промежутке

.

.

Ответ:

.
3 корня уравнения на промежутке

.

Пример.
Решите уравнение

Решение

ОДЗ:

.

Исходное
уравнение равно нулю тогда, когда числитель равен нулю

Подстановка
для упрощения уравнения t = cosx

Обратная
замена переменной t

,

но
корень

не
удовлетворяет области определения, поэтому остается корень

.

Ответ:

.

Пример.
Решите уравнение

Решение

ОДЗ:

Исходное
уравнение равно нулю тогда, когда числитель равен нулю

Ответ:

Пример.
Решить уравнение

Решение

sin2α
+ cos2α
= 1

sin2α
= 2sinαcosα

Помножим
на 2

Теорема косинусов

Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.

Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:

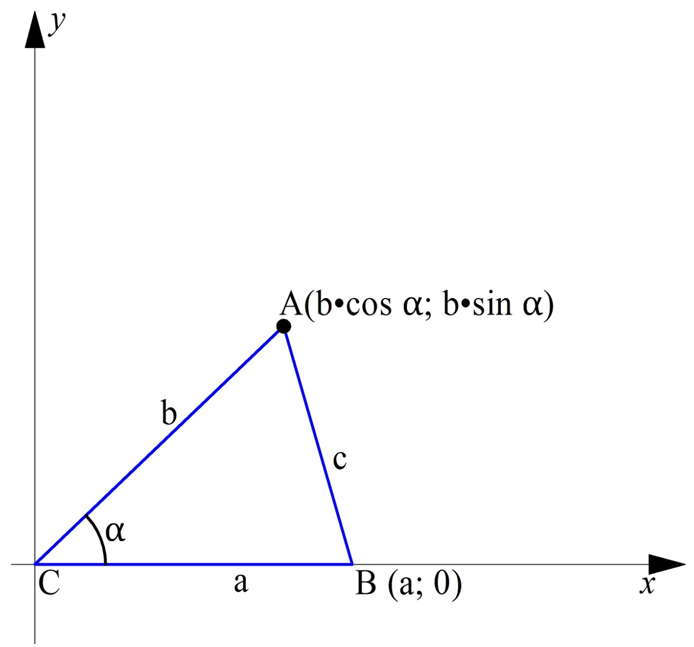
Обозначим угол между а и b как α. Тогда координаты А будут определяться так:

Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с2:

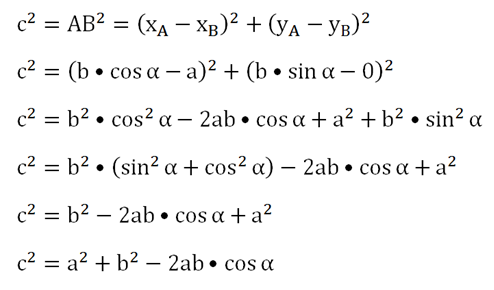
Полученное соотношение как раз и является теоремой косинусов.

Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:

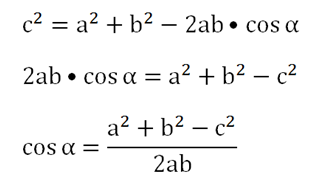
Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.

Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.

Задание. Решите ∆MNE, если

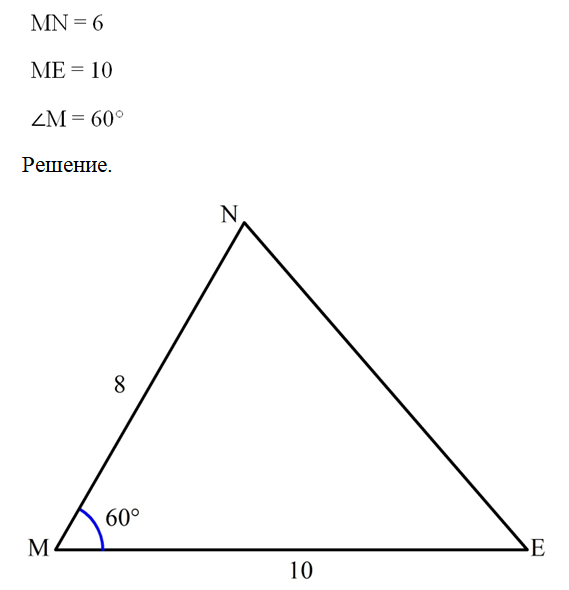
Решение. По теореме косинусов находим сторону NE:

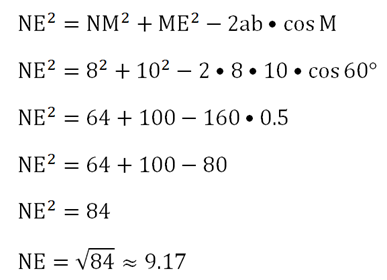
Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:

Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что

Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде

При желании перевести сотые доли в минуты следует дробную часть умножить на 60:

Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что

Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.

Решение.

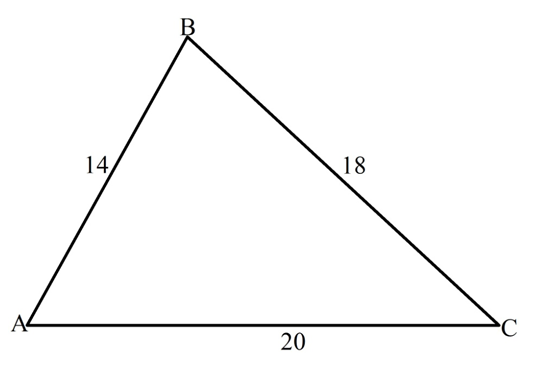
Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:

∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:

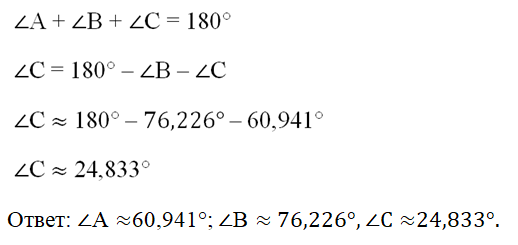
Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.

Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?

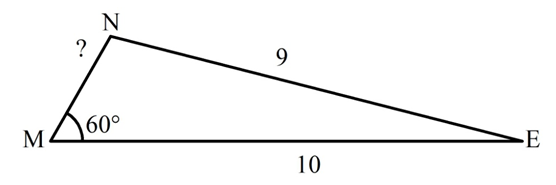
Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:

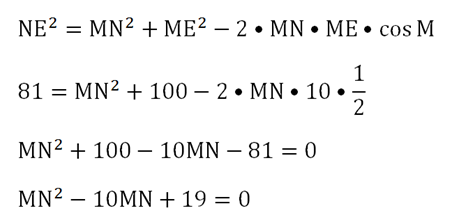
Получили квадратное уравнение, решить его можно через дискриминант:

В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.

Пример задачи на использование формул тригонометрии

sin5x·cos3x − sin8x·cos6x = 0.

Имеем две разные функции sin() и cos() и четыре! разных аргумента 5x, 3x, 8x и 6x. Без предварительных преобразований свести к простейшим типам тригонометрических уравнений не получится. Поэтому сначала пробуем заменить произведения на суммы или разности функций. Делаем это так же, как в примере выше (см. раздел ).

sin(5x + 3x) + sin(5x − 3x) = 2·sin5x·cos3x
sin8x + sin2x = 2·sin5x·cos3x

sin(8x + 6x) + sin(8x − 6x) = 2·sin8x·cos6x
sin14x + sin2x = 2·sin8x·cos6x

(sin8x + sin2x)/2 − (sin14x + sin2x )/2 = 0.

xxxxxx

Уравнение значительно упростилось, но решать его так sin8x = sin14x, следовательно 8x = 14x + T, где Т — период, неверно, так как мы не знаем значения этого периода. Поэтому воспользуемся тем, что в правой части равенства стоит 0, с которым легко сравнивать множители в любом выражении.
Чтобы разложить sin8x − sin14x на множители, нужно перейти от разности к произведению. Для этого можно воспользоваться формулой разности синусов, или снова формулой суммы синусов и нечётностью функции синус (см. пример в разделе ).

sin8x − sin14x = sin8x + sin(−14x) = 2·sin 8x + (−14x)__________   2·cos 8x − (−14x)__________   2  = sin(−3x)·cos11x = −sin3x·cos11x.

Итак, уравнение sin8x − sin14x = 0 равносильно уравнению sin3x·cos11x = 0, которое, в свою очередь, равносильно совокупности двух простейших уравнений sin3x = 0 и cos11x = 0. Решая последние, получаем две серии ответовx₁ = πn/3, nϵZx₂ = π/22 + πk/11, kϵZ

Если Вы обнаружили ошибку или опечатку в тексте, сообщите о ней, пожалуйста, на электронный адрес mathematichka@yandex.ru. Буду весьма признательна.

 Перейти  на главную страницу сайта.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы?   пожелания?  замечания? Обращайтесь —
  mathematichka@yandex.ru

Внимание, mathematichka. Прямое копирование материалов на других сайтах запрещено

Ставьте ссылки.