Разрядные слагаемые. представление числа в виде суммы разрядных слагаемых

Определение разрядных слагаемых чисел

Разрядные слагаемые числа – это способ представления числа в виде суммы, где каждое слагаемое соответствует определенному разряду. Разряд – это позиция цифры в числе, начиная справа и увеличивая разрядность в сторону слева. Например, в числе 2345 первая цифра (5) находится в разряде единиц, вторая (4) – в разряде десятков, третья (3) – в разряде сотен, а четвертая (2) – в разряде тысяч.

Каждое разрядное слагаемое получается, умножая цифру на соответствующий ей порядок в числе (например, единицы, десятки, сотни, тысячи и т.д.). Сложение разрядных слагаемых позволяет получить исходное число.

Применение разрядных слагаемых используется, например, при умножении чисел методом вертикальной множительной, при поиске суммы квадратов чисел от 1 до n и в других математических задачах.

Таким образом, понимание понятия разрядных слагаемых чисел позволяет более глубоко понимать процессы математических операций и ориентироваться в сложных вычислениях.

Примеры разрядных слагаемых

Разрядные слагаемые — это числа, которые складываются по разрядам. Разряды чисел разделяются на единицы, десятки, сотни и тысячи. Посмотрим на несколько примеров разрядных слагаемых:

• Пример 1:

  Сложим числа 123 и 456:

  1	2	3
  + 4	+ 5	+ 6
  —	—	—
  5	7	9

  В данном примере разряды чисел выровнены по позиции (единицы со слагаемыми, десятки со слагаемыми и т.д.). Затем, слагаемые по разрядам складываются и получается результат: 579.

• Пример 2:

  Сложим числа 987 и 123:

  9	8	7
  + 1	+ 2	+ 3
  —	—	—
  10	10	10

  В данном примере также производится сложение по разрядам. Однако, в столбике сложения возникает перенос в разряд десятков, поэтому полученные результаты в разряде единиц сокращаются до 0, а в разряде десятков переносится единица. Этот процесс продолжается далее и в данном примере результат равен 1110.

• Пример 3:

  Сложим числа 2345 и 6789:

  2	3	4	5
  + 6	+ 7	+ 8	+ 9
  —	—	—	—
  8	1	3	4

  В данном примере происходит сложение чисел по разрядам, но в столбике сложения возникают переносы в разрядах десятков, сотен и тысяч. Поэтому в результате получается число 8134.

Сводка происшествий

В результате падения трех подбитых системой ПВО ракет в Новом Осколе в Белгородской области пострадал мужчина. Об этом в своем телеграм-канале сообщил губернатор региона Вячеслав Гладков. Российская система противовоздушной обороны (ПВО) сработала в Новом Осколе, сбив три ракеты. Об этом сообщил губернатор Белгородской области Вячеслав Гладков. На данный момент известном об одном пострадавшем. Огнеборцы региона устранили последствия ДТП в Новом Осколе. Об этом сообщили в пресс-службе ГУ МЧС России по Белгородской области. 31 мая в 18:52 поступило сообщение о дорожно-транспортном происшествии в Новом Осколе.

Классы.

Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам.
Первый класс справа называется классом единиц
, второй называется классом тысяч
, третий – классом миллионов
, четвёртый – классом миллиардов,
пятый – классом триллионов
, шестой – классом
квадриллионов
, седьмой – классом
квинтиллионов
, восьмой – классом
секстиллионов
.

Класс единиц
– первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.Класс тысяч
– второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.Класс миллионов
– третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.

Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.

13 миллиардов 562 миллионов 6 тысяч 891.

Разрядные слагаемые: основное определение

Разрядные слагаемые — это числа, которые складывают для получения суммы. В числе каждая цифра занимает определенный разряд — единицы, десятки, сотни, тысячи и т.д. Разрядные слагаемые состоят из цифр, стоящих в одном разряде, и используются при выполнении операций сложения или вычитания.

Для понимания разрядных слагаемых необходимо знать порядок разрядов и их значения. В десятичной системе числения разряды увеличиваются в 10 раз от меньшего разряда к большему. Например, число 1234567 имеет разряды: единицы, десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы.

В операции сложения двух чисел каждое число разбивается на разрядные слагаемые по разрядам. Затем слагаемые в одинаковых разрядах складываются. Если получается число больше 9, то в разряде записывается последняя цифра полученной суммы, а следующая дописывается в следующий разряд. Это называется переносом.

Пример:

1. Сложить числа 235 и 167:

	2	3	5
+	1	6	7
—	—	—	—
	3	9	2

Результатом сложения чисел 235 и 167 является число 392.

В операции вычитания разрядные слагаемые также используются для вычитания в разряде. Если в разряде уменьшаемое число меньше вычитаемого, то необходимо занимать разряд у предыдущего числа и продолжать операцию.

Пример:

1. Вычесть из числа 325 число 137:

	3	2	5
—	1	3	7
	2	—	—

Результатом вычитания числа 137 из числа 325 является число 248.

Разрядные слагаемые являются важным понятием в математике и позволяют выполнять операции сложения и вычитания чисел различной разрядности с помощью правил переноса и займа разрядов.

Разряды и классы чисел

Разряды

единиц

1…9,

десятков

10…90,

сотен

100…900.

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

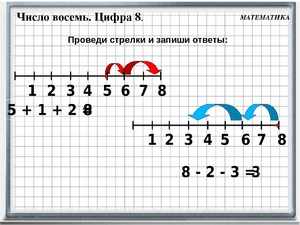Первый — единиц, содержит до 3 знаков:

200 + 10 +3 = 213.

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

40 + 5 = 45,

Сорок пять состоит из четырёх десятков и пяти простых единиц.Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:

1. шестьсот тысяч,
2. семьдесят тысяч,
3. девять тысяч,
4. восемьсот,
5. десять,
6. два,

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

887 213 644,

Это число содержит девять разрядных слагаемых:

1. 800 миллионов,
2. 80 миллионов,
3. 7 миллионов,
4. 200 тысяч,
5. 10 тысяч,
6. 3 тысячи,
7. 6 сотен,
8. 4 десятка,
9. 4 единицы,

7 891 234.

В этом числе нет слагаемых выше 7 разряда. Четвёртый — миллиардов, от 10 до 12 цифр:

567 892 234 976,

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

1. единицы сотен миллиардов,
2. единицы десятков миллиардов,
3. единицы миллиардов,
4. сотен миллионов,
5. десятков миллионов,
6. миллионов,
7. сотен тысяч,
8. десятков тысяч,
9. тысяч,
10. простые сотни,
11. простые десятки,
12. простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего. При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

400 000 000 004,

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса, девятого, восьмого и седьмого третьего и самого́ третьего класса, также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

487 789 654 427 241.

Читается слева:

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

321 546 818 492 395 953,

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31, чем приписывать тридцать один ноль к единице.

Упражнения для тренировки

Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:

• 75 = 70 + 5;
• 324 = 300 + 20 + 4;
• 8434 = 8000 + 400 + 30 + 4;
• 68 486 = 60 000 + 8000 + 400 + 80 + 6;
• 575 783 = 500 000 + 70 000 + 5000 + 700 + 80 + 3;
• 8 633 087 = 8 000 000 + 600 000 + 30 000 + 3000 + 80 + 7.

Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:

• 500 + 60 + 5 = 565;
• 8000 + 300 + 4 = 8304;
• 900 000 + 50 000 + 7000 + 80 + 2 = 957 082.

Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.

Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений

Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.

Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.

Основные правила вычисления разрядных слагаемых

При вычислении разрядных слагаемых важно соблюдать следующие правила:

1. Разрядные слагаемые складываются по разрядам — сначала слагаемые единиц, потом десятков, сотен и т.д.
2. Если в разряде складывается больше десяти единиц, то здесь выполняется перенос единиц в следующий разряд, а оставшаяся часть остается в текущем разряде.
3. Перенос единиц осуществляется путем деления суммы разрядных слагаемых на 10, при этом отбрасывается дробная часть. Оставшаяся целая часть и будет переносимой единицей.
4. Переносимая единица прибавляется к слагаемым в следующем разряде.

Пример:

Разряд	Слагаемое	Переносимая единица	Результат
Единицы	7	—	7
Десятки	5	5
Сотни	9	9
Тысячи	4	4

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

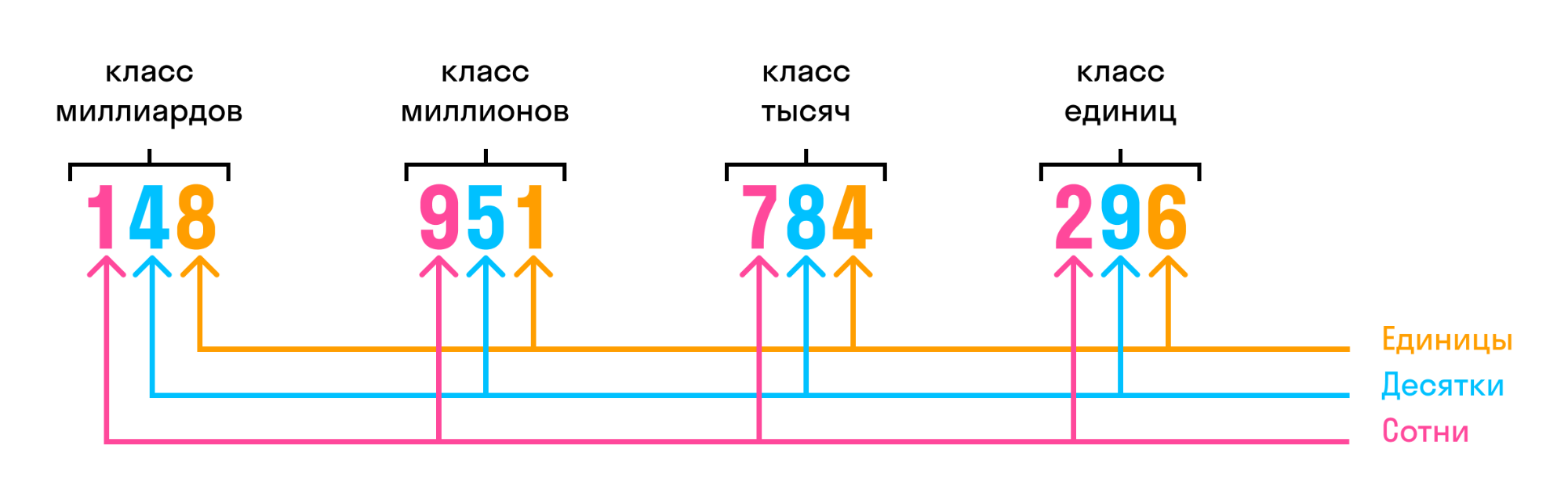
Названия классов многозначных чисел:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

• 10 единиц = 1 десяток;
• 10 десятков = 1 сотня;
• 10 сотен = 1 тысяча;
• 10 тысяч = 1 десяток тысяч;
• 10 десятков тысяч = 1 сотня тысяч;
• 10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

• шести единиц миллионов (6 * 1 000 000);
• пяти десятков тысяч (5 * 10 000);
• семи единиц тысяч (7 * 1000);
• трех сотен (3 * 100);
• восьми десятков (8 * 10);
• шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков. Записываем число без первого разряда (единицы).

3. Определяем количество сотен. Записываем число без первого и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч. Записываем число без первого, второго, третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч. Записываем число без первого, второго, третьего, четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч. Записываем число без десятков тысяч, единиц тысяч, сотен и единиц.

7. Определяем количество единиц миллионов. Записываем число без сотен тысяч, десятков тысяч, единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Разряды и классы чисел

Разряды

Таким образом, мы видим, что числовая мощность числа — это его позиция в файле чисел, и любое значение может быть выражено как nnn = n00 + n0 + n где n — число от 0 до 9.

Дюжина — это вторая единица, а 100 — третья цифра. Первая разрядная единица называется простой, а все остальные — составными.

Для облегчения записи и передачи цифры сгруппированы по трем категориям. Для удобства чтения между классами допускается взаимодействие.

Классы

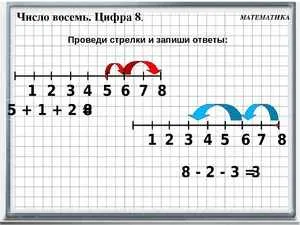
Первая — максимальная трехзначная единица.

213 содержит следующие номера: 200, 110 и первые три единицы.

45 состоит из четырех десятков и первых пяти единиц. Второй — тысячи, от четырех до шести цифр.

Этот итог состоит из суммы следующего разряда.

1. шестьсот тысяч,
2. семьдесят тысяч,
3. девять тысяч,
4. восемьсот,
5. десять,
6. два,

3 456 = 3000 + 400 +50 +6.

За четвертой цифрой нет итога.

Третья — миллионы, 7-9 цифр.

Этот номер содержит девятизначный итог.

1. 800 миллионов,
2. 80 миллионов,
3. 7 миллионов,
4. 200 тысяч,
5. 10 тысяч,
6. 3 тысячи,
7. 6 сотен,
8. 4 десятка,
9. 4 единицы,

7 891 234.

Это число не содержит итогов, превышающих седьмую цифру. Четвертый, миллиарды, от 10 до 12 цифр:.

567 млрд 892 млн 234 тыс. 976.

Цифры в категории 4 читаются слева направо.

1. единицы сотен миллиардов,
2. единицы десятков миллиардов,
3. единицы миллиардов,
4. сотен миллионов,
5. десятков миллионов,
6. миллионов,
7. сотен тысяч,
8. десятков тысяч,
9. тысяч,
10. простые сотни,
11. простые десятки,
12. простые единицы.

Цифры нумеруются, начиная с наименьшей и заканчивая наибольшей. Если в общем числе нет промежуточного значения, запись вводится с нулями, а название отсутствующей цифры и разряда единицы не произносится:.

4 000 миллиарда 4. Здесь не произносятся названия следующих посадок, потому что они отсутствуют: десятая и одиннадцатая четвертого класса, девятая, восьмая и седьмая третьего, десятая третьего, названия второго класса и их посадки не произносятся, а их сотни — десятки единиц.

Пятая — триллионы, тринадцать-пятнадцать цифр.

487 триллионов 799 миллиардов 665 миллионов 427 миллионов 441.

Разрядные слагаемые в математике

Число — это математическое понятие, которое также используется для количественного описания части или частей ряда, сравнения целого с его частями и расположения их по порядку. Значение числа представлено различными комбинациями символов или цифр. Сегодня цифры от 1 до 9 и 0 используются практически везде. Числа в виде семи латинских букв используются редко и здесь не рассматриваются.

В списке: «1, 2, 3 … 44» или непрерывная схема: «1-й, 2-й, 3-й … 44» используются натуральные числа, называемые натуральными числами. Все множество называется «рядом натуральных чисел», обозначаемым латинской буквой n. Всегда существует большее число и нет конца, так как нет больших чисел.

Сумма разрядных слагаемых

Умение решать простые примеры в уме — полезный навык. Конечно, у вас всегда будет с собой смартфон, но гораздо лучше и эффективнее сделать это самостоятельно и гордиться собой. Существует множество приемов, позволяющих упростить умственные вычисления. Сложение чисел — один из них.

Эта статья поддерживается методистами SkySmart. Если вы обнаружили ошибку, обратитесь к интерактивной беседе (справа внизу на экране).

Сумма разрядных слагаемых

Каждое натуральное многозначное число может быть выражено как сумма цифровых компонентов. Сумма цифровых компонентов может быть записана как.

35 = 3 ТЭНС + 5 единиц = 3*10 = 30 + 5 = 35.

30 — сумма цифр — 5 — сумма цифр.

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 цифр Pumper — 5 цифр резюме.

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300 + 50 + 6 = 356.

300, 50 и 6 — это сумма цифр.

Онлайн-курсы математики для детей помогают улучшить оценки и подготовиться к контрольным работам, IEP и экзаменам.

Разряды и классы чисел

Чтобы легко записывать числа в виде суммы цифр, учащиеся должны уметь правильно определять порядок и деление многих чисел.

В многозначных числах цифры справа налево делятся на группы из трех цифр. Эти группы называются классами.

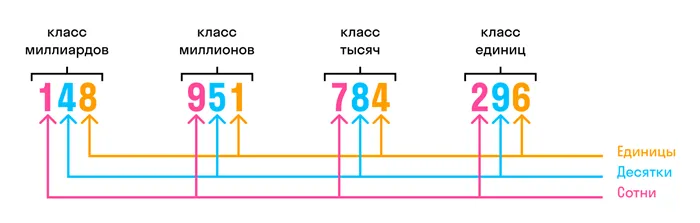
Название многозначного номера:.

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы избежать преобразования многозначного числа при чтении в загадку, рекомендуется при записи определять число в классе. Следующее:.

Такие числа читаются слева направо.

Числа — это многозначные числа, в которых цифра занимает разряд.

Числа измеряются справа налево. Первая цифра справа от числа — это первая цифра.

Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Числа — это единицы, десятки, сотни, миллионы и миллионы.

Все цифровые единицы, кроме простых, являются сложными единицами. На каждые 10 единиц одного числа приходится одна единица следующего числа.

• 10 единиц = 1 десяток;
• 10 десятков = 1 сотня;
• 10 сотен = 1 тысяча;
• 10 тысяч = 1 десяток тысяч;
• 10 десятков тысяч = 1 сотня тысяч;
• 10 сотен тысяч = 1 миллион.

Если одна сложная единица больше другой, она называется высшей дивизионной единицей. Если он меньше, его называют подразделением низшего дивизиона. Так, например, 100 единиц — это более высокая единица измерения расстояния по сравнению с 10 единицами, но более низкая по сравнению с 1000 единицами.

Особенности разложения

Чтобы лучше понять цифровые компоненты и их использование в математике, стоит подробно рассмотреть процесс разложения натуральных величин на эти компоненты. В основе большинства проблем с суммами цифр лежит деление натуральных чисел, т.е. представление их в виде суммы цифр путем сложения количеств всех разрядных единиц.

Сложные натуральные числа, т.е. многозначные (например, двузначные, трехзначные и т.д.), могут быть преобразованы в суммы цифровых компонентов. Чтобы правильно разделить число на цифры, необходимо соблюдать основные правила. Во-первых, нули не учитываются при построении цифр числа. Во-вторых, добавки перечислены в порядке приоритета. То есть, сверху вниз, сначала тысячи, потом сотни, потом десятки. Последний вариант прост.

Состав чисел может быть описан тремя способами

• базовый — простое сложение: 852768 = 800 000 + 50 000 + 2000 + 700 + 60 + 8;
• подробный — сложение с умножением единиц разряда на их количество: 852768 = 8*100 000 + 5*10 000 + 2*1000 + 7*100 + 6*10 + 8*1.
• словесный — текстовая расшифровка: 852768 = восемь сотен тысяч, пять десятков тысяч, две тысячи, семь сотен, шесть десятков, восемь простых единиц.

Десятичная система счисления

Для записи чисел в математике используется десятичная позиционная система счисления. В этой системе применяются $10$ цифр:

Рисунок $1$ Современные цифры и их «предки»

числа и цифры

Важно не путать числа с цифрами. Чисел бесконечно много, цифр — $10$

интересный факт

Сначала люди записывали цифры черточками и точками. Позднее изобрели римские цифры ($1 — I, 2 — II, 3 — III$ и т. д.). На Востоке была изобретена десятичная система счисления, пришедшая в Европу в Средние века.

{«questions»:,»explanations»:,»answer»:}}}]}. позиционная система счисления

позиционная система счисления

Разберем число $\textcolor{blue}{9}\textcolor{coral}{9}\textcolor{orange}{9}$. Оно состоит из трех одинаковых цифр, но позиция этих цифр отличается, по этому принципу меняется и разряд. Первая справа цифра — $\textcolor{orange}{девять \space единиц}$,цифра посередине — $\textcolor{coral}{девять \space десятков}$,цифра слева — $\textcolor{blue}{девять \space сотен}$.

Значение цифры зависит от ее позиции, десятичную систему счисления традиционно называют позиционной.

пример

В числе $555$ первая справа цифра означает $5$ единиц, вторая $5$ означает $5$ десятков, а третья — $5$ сотен.

Число $10$

$10$ единиц образует десяток, $10$ десятков образует сотню, $10$ сотен — тысячу:

• $1$ — единица;
• $10$ — десять;
• $100$ — сто;
• $1000$ — тысяча;
• $10\space000$ — десять тысяч;
• $100\space 000$ — сто тысяч;
• $1 \space000\space 000$ — миллион;
• $10 \space000\space 000$ — десять миллионов;
• $100 \space000\space 000$ — сто миллионов;
• $1 \space000\space 000\space 000$ — миллиард;
• $10\space 000\space 000\space 000$ — десять миллиардов и т. д.

Интерактив

Изменяйте цифру разряда, чтобы получить новое число.

digits

{"questions":,"answer":0}},"explanation":"В десятичной системе значение цифры зависит от ее позиции в числе. Если переставить цифры, получится другое число. Например, $54$ не равно $45$."}]}

Последние новости России и мира

Можно представить, какими могли быть разрушения в мирном городе, в 80 километрах от границы. Сбитыми обломками все же задело несколько частных домов, мужчина получил ранение руки. И еще уже из сводки Минобороны. Там рассказали об успешном продвижении наших войск и уничтожении большого количества боевиков.

При этом каких-либо официальных комментариев от властей по этому не поступало. Также неизвестно о каких-либо последствиях громких звуков.

Отправить опечатку.

Средство массовой информации сетевое издание «Городской информационный канал m24. Учредитель и редакция — АО «Москва Медиа». Главный редактор И. Адрес редакции: 125124, РФ, г.

Как выяснилось позже, беспилотник зацепил провода ЛЭП в районе поселка Северный. На данный момент электроснабжение восстановлено. Ваша реакция на сюжет?

Примеры записи суммы разрядных слагаемых чисел

Существует несколько способов записи суммы разрядных слагаемых чисел:

1. Запись чисел в столбик: Числа располагаются друг под другом, при этом суммируются цифры одного разряда. Результат заносится в запас по правому краю.
2. Запись чисел в строку: Цифры одного разряда располагаются друг под другом и суммируются сразу. При этом результат суммирования каждого столбца выводится в строку слева направо.
3. Запись в виде таблицы: Числа располагаются в таблице, где каждая строчка отвечает за один разряд. В первом столбце указываются числа, второй столбец отведен для разрядных слагаемых, а в третьем столбце записывается результат суммирования.

Например, для суммы чисел 1234 и 5678 мы можем записать:

	1	2	3	4
+	5	6	7	8
	6	8	10	12

Как видно из таблицы, результат суммы равен 6912.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

1. 84 610 84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10 84 610 = 80 000 + 4 000 + 600 + 10.
2. 45 317 45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17 45 317 = 40 000 + 5 000 + 300 + 17.
3. 56 789 56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9 56 789 = 50 000 + 6 000 + 700 + 80 + 9.
4. 345 677 345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7 345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
5. 687 543 687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3 687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
6. 877 589 877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9 877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

1. 4 895 634 4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4 4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
2. 8 675 349 8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9 8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
3. 77 897 125 77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5 77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
4. 656 734 212 656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2 656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число

Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете

Источник

Разряды чисел.

Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.

Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.

Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда
.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда.
Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.

Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.

Такой разбор числа называется разрядным составом числа
.

Преимущества и применение разрядных слагаемых

Разрядные слагаемые — это числа, записанные в столбик вертикально, при сложении которых получается сумма. Имея знания о разрядных слагаемых, ученик может производить сложение чисел большой разрядности, а также решать задачи, требующие сложения чисел. Применение разрядных слагаемых позволяет более удобно выполнять сложение, особенно при работе с большими числами.

Преимущества применения разрядных слагаемых:

• Удобство и наглядность: Разрядные слагаемые позволяют выполнять сложение чисел поэтапно, в столбик, что облегчает восприятие процесса и помогает избегать ошибок.
• Расширение возможностей: Знание и использование разрядных слагаемых позволяет решать задачи, требующие сложения чисел большой разрядности, что дает ученику больше возможностей в решении арифметических задач.

Применение разрядных слагаемых включает следующие шаги:

1. Запись чисел в столбик, выровненных по разрядам.
2. Сложение цифр справа налево, начиная с младших разрядов.
3. Перенос единицы в следующий разряд, если сумма цифр в текущем разряде больше 9.
4. Продолжение сложения в следующих разрядах до самого старшего разряда.

Применение разрядных слагаемых позволяет ученику лучше понять структуру и правила сложения чисел, что является важным этапом в развитии математического мышления и навыков решения задач.