Решение систем линейных уравнений методом подстановки и методом сложения

Содержание

• Слайд 1

  Линейное уравнение
  с двумя переменными.
  График линейного уравнения
  с двумя переменными

• Слайд 2

  проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала;
  развивать познавательные способности учеников; расширение кругозора учащихся; развитие внимания, логического мышления.
  воспитывать активность, самостоятельность; воспитание основ здорового образа жизни, формирование бережного отношения учащихся к своему здоровью;

• Слайд 3

• Слайд 4

  Повторение:

  1) Дать определение линейного уравнения
  с двумя переменными.
  2) Что называется решением уравнения с двумя переменными?
  3) Какое уравнение называется равносильным данному?
  4) Что называется графиком уравнения с двумя переменными?

  Дальше

• Слайд 5

  Линейным уравнением с двумя переменными называется уравнение вида ах+by=c,
  где хи у – переменные,
  а, bи с­ некоторые числа.

• Слайд 6

  Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

• Слайд 7

  Уравнения с двумя переменными, имеющие одни и те же корни, называются равносильными.

• Слайд 8

  Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

• Слайд 9

  Историческая справка.

  Рене Декарт (1596-1650)− французский философ, математик и физик. Создал основы аналитической геометрии, ввел понятие переменной величины, разработал метод координат. Осуществил связь алгебры с геометрией.

  Пьер Ферма (1601-1665) − французский математик, один из создателей аналитической геометрии и теории чисел. Занимался теорией решения алгебраических уравнений с несколькими переменными.

• Слайд 10

  Ответ: а)3х – у = 14
  г) 5х + 2у = 16

• Слайд 11

  2х + 5у = 12

  а)А(-1; -2), б)В(2; 1), в)С(4; -4), г)D(11; -2).

  Ответ: г)D(11; -2).

• Слайд 12

  x

  8

  6

  4

  2

  -2

  е ж з и к л м
  а б в г д
  у ф х ц ч ш щ
  й э ю я п р с
  н о т й

  (6;4) (-2;-2) (4;4) (-2;-2) (4;6) (-6;4) (0;2)
  М О Л О Д Е Ц

  y
  №2. «Угадай слово»

  -8 -6 -4 -2 0 2 4 6 8

• Слайд 13

  № 1045 (д),
  № 1048 (г, д),
  № 1050 (г).

• Слайд 14

  №1045. д) Принадлежит ли графику уравнения 3х+4у=12 точка D(0,3)?
  3х+4у=12
  3*0+4*3=12,
  12=12 (да).

• Слайд 15

  г) 0,5у-х=1,
  0,5у=1+х,
  у=2+2х

  д) 1,2х=-4,8,
  х=-4

  х
  у
  0

  2
  1
  3
  4
  1
  2
  -1
  -2
  -3
  -4

  0,5у-х=1

  1,2х=-4,8

• Слайд 16

  №1050. Постороить график уравнения
  г) (х+у)-(х-у)=4,
  х+у-х+у=4,
  2у=4,
  у=2. (х+у)-(х-у)=4

  х
  у

  0
  2

  1

• Слайд 17

  №4. Самостоятельная работа

  Вариант 1
  Трудность 1
  1.Выразите переменную у через х: у+4х=6.
  2. Принадлежит ли графику
  уравнения 4х+2у=6 точка А(-2;3)?
  Трудность 2
  3. Выразите переменную
  х через у: 10у-6х=30.
  4. Построить график уравнения 2х+у=4.
  Трудность 3
  Сахар расфасован в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получить 20 кгсахара?

  Вариант 2
  Трудность 1
  1.Выразите переменную у через х: у-3х=6 .
  2. Принадлежит ли графику
  уравнения 4х+2у=6 точка В(-1;5)?
  Трудность 2
  3. Выразите переменную
  х через у: 12у-4х=20.
  4. Построить график уравнения
  5х + у – 4 = 0 .
  Трудность 3
  Ваня купил ручки по 5 руб.
  И тетради по 7 руб. Сколько
  ручек и тетрадей купил Ваня,
  если за всю покупку он заплатил 44 руб.?

• Слайд 18

  На прямой, являющейся графиком уравнения 3х+1=у, взята точка, абсцисса которой равна 0. Найдите ординату этой точки.

• Слайд 19

  Вариант 1
  1. у=6-4х
  2. нет
  3. х=-5+5/3у
  4.
  Вариант 2
  1. у=6+3х
  2. да
  3. х=-5+3у
  4.

  у
  х
  0
  2
  4

  х
  у
  0
  1
  -1
  4

  2 (3кг) и 7 (2кг);
  4 (3кг) и 4 (2кг);
  6 (3кг) и 1 (2кг);
  5. 6 ручек и 2 тетради

• Слайд 20

  у=3х+1

  х
  у
  0

  1
  -1
  -2
  Ответ: (0;1)

• Слайд 21

• Слайд 22

  п.41,42
  (1) № 1049 (а, б), 1052;
  (2) №1054(6), 1055 (а);
  (3 ) № 1141.
  Домашняя работа:

• Слайд 23

  Спасибо за урок!

Посмотреть все слайды

Способ сложения

Если даны два верных равенства в системе уравнений, то можно складывать их правые и левые части, и равенство получится тоже верным.

В системе линейных уравнений складывать нужно левые и правые части каждого из них. Для того, чтобы избавиться, если это возможно, от одной из переменных. Цель — прийти к простому уравнению с одной переменной, которое не требует сложного решения.

Пошаговое решение 

\(\left\{\begin{array}{l}2n-5m=8\\n+5m=19\end{array}\right.\)

1. Надо сложить отдельно правую часть первого уравнения с правой частью второго, а левую — с левой.

2n−5m+n+5m=8+19

2. Произвести необходимые вычисления (привести подобные в левой части и произвести сложение в правой) и найти значение одной из переменных. Получится:

3n=27

n=27÷3

n=9

3. Подставить полученное значение n в одно из уравнений системы (в любое), чтобы найти значение второй переменной. Выберем, например, уравнение номер 1:

2×9−5m=8

18−5m=8

−5m=8−18

−5m=−10

m=2

Ответ: n=9, m=2.

Замечание при решении уравнения

В примере выше изначально были даны уравнения с одинаковыми по модулю коэффициентами слагаемых (−5m и 5m). Такое явление нельзя назвать частым. Поэтому необходим навык приведения любых уравнений системы к такому виду. Для этого нужно научить способу домножения обеих частей уравнения на одно и тоже число, не равное нулю. 

Пример

\(\left\{\begin{array}{l}4v+9t=1\\5v-18t=-28\end{array}\right.\)

В уравнении номер 2 видим переменную с числовым коэффициентом −18. А в первом ту же переменную с коэффициентом 9. Нам нужно сделать так, чтобы эта переменная убралась. Для этого нужно из 9 сделать 18. Возьмем уравнение номер 1. Произведем умножение обеих его частей на 2. Получим:

8v+18t=2

Теперь в обоих уравнениях есть одинаковые слагаемые, которые можно сократить. Для этого выполним метод сложения соответствующих частей обоих уравнений друг с другом.

Получим:

8v+18t+5v−18t=2+(−28)

13v=−26

v=−26÷13

v=−2

Теперь можно поставить полученное значение v в первое (или в любое) уравнение, чтобы найти t:

4×(−2)+9t=1

−8+9t=1

9t=1+8

9t=9

t=1

Ответ: v=−2, t=1

Примеры решения систем уравнений других видов

Пример 8
. Решить систему уравнений (МФТИ)

Решение
. Введем новые неизвестные u
и v
, которые выражаются через x
и y
по формулам:

Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x
и y
через u
и v
. Из системы (13) следует, что

Решим линейную систему (14), исключив из второго уравнения этой системы переменную x .
С этой целью совершим над системой (14) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (14) преобразуется в равносильную ей систему

из которой находим

Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде

У системы (16) первое уравнение — линейное , поэтому мы можем выразить из него неизвестное u
через неизвестное v
и подставить это выражение во второе уравнение системы.

просмотров

Способ введения новых переменных

Это свойство систем уравнений имеет целью упрощение этих систем для более быстрого решения.

Существует два варианта подобного пути:

• введение одной новой переменной и только в одном уравнении системы;
• введение двух новых переменных в обоих уравнениях в одно и то же время.

Как вводить новую переменную

Новая переменная\ые вводятся вместо повторяющихся в уравнении сочетаний, заменяют их и тем самым упрощают всю систему. В результате замены получается два простых линейных уравнения, которые легко решаются.

Пример 1

\(\left\{\begin{array}{l}mn\times\begin{pmatrix}m&+n\end{pmatrix}=6\\mn+\begin{pmatrix}m&+n\end{pmatrix}=5\end{array}\right.\)

Вводим 2 новые переменные: вместо mn будет t, а вместо m+n поставим z. Это поможет упростить систему, получится:

\(\left\{\begin{array}{l}t\times z=6\\t+z=5\end{array}\right.\)

Далее легко найти значения переменных в получившихся уравнениях: 

\(\left\{\begin{array}{l}t_1=2\\z_1=3\end{array}\right.\)

и

\(\left\{\begin{array}{l}t_2=3\\z_2=2\end{array}\right.\)

Далее нужно просто подставить эти значения вместо тех, которые заменяли введенные переменные, и дорешать получившиеся уравнения.

Пример 2

\(x\left\{\begin{array}{lc}\frac2{2m-n}&+\frac3{m-2n}=\frac12\\\frac2{2m-n}&-\frac1{m-2n}=\frac1{18}\end{array}\right.\)

Вводим новые переменные: 

\(\frac2{2m-n} \)

заменим на t, а вместо

\(\frac1{m-2n}\)

поставим z. Теперь система примет такой вид: 

\(\left\{\begin{array}{l}t+3z=\frac12\\t-z=\frac1{18}\end{array}\right.\)

Далее по методу сложения вычтем второе уравнение из первого. Получим:

\(\left\{\begin{array}{l}4z=\frac49\\t=\frac1{18}+z\end{array}\right.\)

Вычисляем корни, имеем:

\(\left\{\begin{array}{l}z=\frac19\\t=\frac16\end{array}\right.\)

Теперь вернем старые переменные:

\(\left\{\begin{array}{l}\frac2{2m-n}=\frac16\\\frac1{m-2n}=\frac19\end{array}\right.\)

Преобразуем:

\(\left\{\begin{array}{l}2m-n=12\neq0\\m-2n=9\neq0\end{array}\right.\)

Дальше используем подстановку:

\(\left\{\begin{array}{l}2\begin{pmatrix}9&+2n\end{pmatrix}-n=12\\m=9+2n\end{array}\right.\)

Решаем оба уравнения. В первом получается:

18+4n-n=12

3n=−6

n=−2

Во втором имеем:

m=9+2n

Подставляем значение n=−2: 

m=9+(2×(−2)

m=9+(−4)

m=5

График уравнения

Любое действительное число можно отметить на координатной прямой, а пару чисел – на координатной плоскости. Если же нанести на плоскость все возможные решения, то получим какую-то линию, которую принято считать графиком уравнения.

Для построения графика можно с помощью тождественных преобразований свести уравнение к функции, а потом построить график этой функции.

Рассмотрим это на примере следующего уравнения:

y — x2 = 0

Попытаемся выразить у через х.

Для этого перенесем в уравнении слагаемое (– x2) вправо:

y = x2

Получили степенную функцию, чей график нам известен. Он представляет собой параболу (см. урок Функции) График исходного уравнения выглядит также:

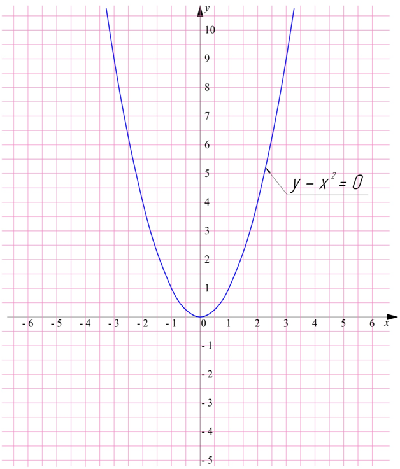
Однако график функции и график уравнения – это разные понятия. Дело в том, что ряд уравнений невозможно свести к функции. Например, для равенства

x2 + y2 = 25

Однако график функции и график уравнения – это разные понятия. Дело в том, что ряд уравнений невозможно свести к функции. Например, для равенства

0 + y2 = 25

Решая его, получаем два корня

y2 = 25

y = -5 и y = 5

В результате мы нашли две точки для графика, (0; 5) и (0; – 5).

Теперь подставим другое значение х, например, х = 3:

32 + y2 = 25

y2 = 16

y = -4 и y = 4

Нашли ещё 2 точки: (3; 4) и (3; – 4)

Далее примем х = 4, получим уравнение:

42 + y2 = 25

y2 = 9

y = -3 и y = 3

таким образом нашли точки (4; – 3) и (4; 3).

Аналогичным образом, подставляя вместо х числа 5, – 5, – 4, – 3, можно найти точки (5; 0), (– 5; 0), (– 4; 3), (– 4; – 3), (– 3; 4) и (– 3; – 4). Отметим их все и соединим плавной линией:

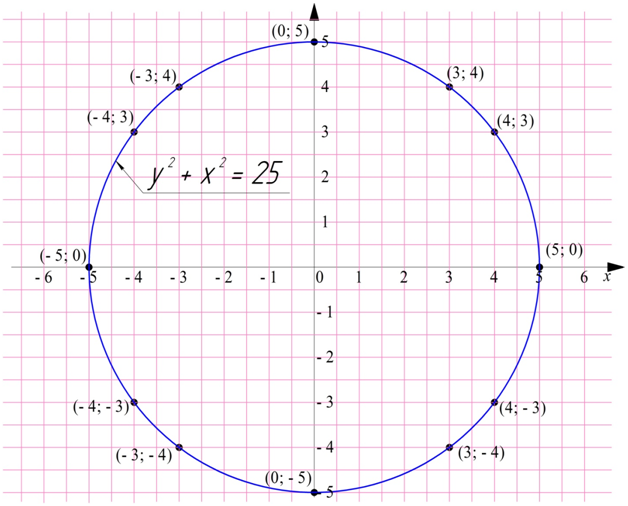
График выглядит как окружность (Позднее, в 10 классе, будет строго доказано, что это именно окружность).

Окружность не может являться графиком функции, так как одному значению x должно соответствовать единственное значение у. Однако на рисунке видно, что для х = 0 подходит два значения у: 5 и – 5.

Удобные онлайн-калькуляторы

В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.

Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.

https://youtube.com/watch?v=YTeq45NJJ78

Решение системы методом почленного сложения (вычитания) уравнений системы

В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, впрочем, сейчас станет всё понятнее.

Пример 4

Решить систему линейных уравнений:

Я взял ту же систему, что и первом примере.
Анализируя систему уравнений, замечаем, что коэффициенты при переменной  одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:

Действия, обведенные красным цветом, выполняются МЫСЛЕННО.
Как видите, в результате почленного сложения у нас пропала переменная . В этом, собственно, и состоит суть метода – избавиться от одной из переменных.

Теперь всё просто:  – подставляем в первое уравнение системы (можно и во второе, но это не так выгодно – там числа больше):

В чистовом оформлении решение должно выглядеть примерно так:

Ответ:

У некоторых явно возник вопрос: «Зачем все эти изыски, если можно просто выразить одну переменную через другую и подставить во второе уравнение?».

Пример 5

Решить систему линейных уравнений:
В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.

Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:

Как видим числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Таким образом, хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.

Будем рассматривать коэффициенты при переменной :

Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, то можно просто перемножить коэффициенты:

Далее:
Первое уравнение умножаем на
Второе уравнение умножаем на

В результате:

Вот теперь из первого уравнения почленно вычитаем второе. На всякий случай привожу еще раз действия, которые проводятся мысленно:
Следует отметить, что можно было бы наоборот – из второго уравнения вычесть первое, в результате получится равносильное уравнение с противоположными знаками.

Теперь подставляем найденное значение  в какое-нибудь из уравнений системы, например, в первое:

Ответ:

Решим систему другим способом. Рассмотрим коэффициенты при переменной

Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.
Для этого первое уравнение умножаем на 3, второе уравнение  умножаем на 4:

Почленно складываем уравнения и находим значения переменных: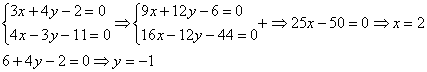

Ответ:

Второй способ несколько рациональнее, чем первый, так как складывать проще и приятнее чем вычитать.

В высшей математике всегда стремимся складывать и умножать, а не вычитать и делить.

Пример 6

Решить систему линейных уравнений:

Это пример для самостоятельного решения (ответ в конце урока).

Продолжение урока на странице Правило Крамера. Метод обратной матрицы >>>

(Переход на главную страницу)

Нелинейные уравнения с двумя неизвестными

Определение 1
. Пусть A
— некоторое

множество пар чисел

(

x

;

y

) .
Говорят, что на множестве A
задана

числовая функция

z

от двух переменных

x
и y ,
если указано правило, с помощью которого каждой паре чисел из множества A
ставится в соответствие некоторое число.

Задание числовой функции z
от двух переменных x
и y
часто

обозначают

так:

где

f

(

x

,

y

)

– любая функция, отличная от функции

f

(

x

,

y

) =

ax +by + c

,

где a , b , c
–

заданные числа

.

Определение 3
.

Решением уравнения (2)

называют пару чисел (

x

;

y

) ,
для которых формула (2) является верным равенством.

Пример 1
. Решить уравнение

Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x
и y
удовлетворяют системе уравнений

решением которой служит пара чисел (6 ; 3) .

Ответ
: (6 ; 3)

Пример 2
. Решить уравнение

Следовательно, решением уравнения (6) является

бесконечное множество пар чисел

вида

(1 +

y

;

y

) ,

где y
– любое число.

Пример.

Рассмотрим уравнение плоскости как систему \tag{12}Ax+By+Cz+D=0 из одного уравнения. Пусть A \neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0. Мы получим x=-D/A. Так как n=3, r=1, фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1, z=0 и y=0, z=1. Соответствующие значения базисной неизвестной x, найденные из приведенной системы, будут -B/A и -C/A. Итак, общее решение системы \tag{13} \begin{Vmatrix} x\\ y\\ z \end{Vmatrix}=\begin{Vmatrix} -D/A\\ 0\\ 0 \end{Vmatrix}+c_{1} \begin{Vmatrix} -B/A\\ 1\\ 0 \end{Vmatrix}+c_{2} \begin{Vmatrix} -C/A\\ 0\\ 1 \end{Vmatrix}.

Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение \begin{Vmatrix} -D/A& 0& 0 \end{Vmatrix}^{T} состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже , что компоненты лежащих в плоскости векторов удовлетворяют уравнению A\alpha_{1}+B\alpha_{2}+C\alpha_{3}=0, то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула — не что иное, как параметрические уравнения плоскости.

Основные виды систем уравнений

В математике насчитывается достаточно много видов систем уравнений. Для более удобного их изучения и нахождения решений их разделяют на несколько групп с определёнными характеристиками.

Классификация помогает рассматривать системы уравнений разных видов. Первый вариант – это классифицирование по количеству уравнений в системе. Если оно всего одно, то его называют обычным уравнением. Если уравнений несколько, тогда речь идет о системе.

Отличительным критерием для другого вида классификации является количество переменных. Если переменная одна, значит это уравнение с одной неизвестной, если их две – то с двумя неизвестными и т.д.

Метод подстановки

Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

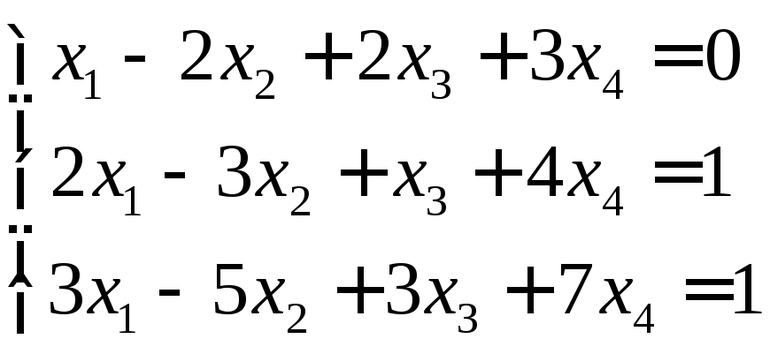
• через n в одном из уравнений выражают m;
• подставляют полученное равенство вместо n в другое тождество;
• решают уравнение и находя m;
• поочерёдно подставляют найденные корни и получают ответ.

8 * n – 5 * m = -16.

10 * n + 3 * m = 17.

Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.

Системы из трех линейных уравнений с тремя неизвестными

      Определение 7. Системой из трех линейных уравнений с тремя неизвестными   x ,   y     и   z   называют систему уравнений, имеющую вид

(10)

где   a₁ ,  b₁ ,  c₁ ,  d₁ ,  a₂ ,  b₂ ,  c₂ ,  d₂ ,  a₃ ,  b₃ ,  c₃ ,  d₃   – заданные числа.

      Определение 8. В системе уравнений (10) числа   a₁ ,  b₁ ,  c₁ ,  a₂ ,  b₂ ,  c₂ ,  a₃ ,  b₃ ,  c₃   называют коэффициентами при неизвестных, а числа   d₁ ,  d₂ ,  d₃   – свободными членами.

      Определение 9. Решением системы уравнений (10) называют тройку чисел   (x ; y ; z) ,   при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

      Пример 4 . Решить систему уравнений

(11)

      Решение. Будем решать систему (11) при помощи метода последовательного исключения неизвестных.

      Для этого сначала исключим из второго и третьего уравнений системы неизвестное   y ,  совершив над системой (11) следующие преобразования:

• первое уравнение системы оставим без изменений;
• ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
• из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

      В результате система (11) преобразуется в ей систему

(12)

      Теперь исключим из третьего уравнения системы неизвестное   x ,  совершив над системой (12) следующие преобразования:

• первое и второе уравнения системы оставим без изменений;
• из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

      В результате система (12) преобразуется в ей систему

(13)

      Из системы (13) последовательно находим

z = – 2 ;   x = 1 ;   y = 2 .

      Ответ.   (1 ; 2 ; –2) .

      Пример 5. Решить систему уравнений

(14)

(15)

      Если числа   (x ; y ; z)   являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа   (x ; y ; z)   должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

      Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) , то полученный результат нужно проверить. Подставив тройку чисел   (3 ; 0 ; –1)   в исходную систему (14), убеждаемся, что числа   (3 ; 0 ; –1)   действительно являются ее решением.

      Ответ:   (3 ; 0 ; –1) .

Системы с тремя переменными

До сих пор мы рассматривали способы решения систем линейных уравнений, в которых фигурировало только 2 неизвестные величины. Однако на практике встречаются и системы уравнений с тремя переменными.

Для их решения можно использовать и способ подстановки, и способ сложения. А вот графический метод здесь уже не поможет. Дело в том, что каждая точка на координатной плоскости представляет собой пару чисел, например, (5; 0), (4; 7) или (– 3; 2). Также и решение систем с двумя неизвестными является парой чисел, что позволяет использовать точки на плоскости для обозначения этих решений. Но решением системы с 3 неизвестными является не пара, а уже тройка чисел, а ее отметить как точку на плоскости не получится.

Рассмотрим задачу. Периметр треугольника равен 30 см. Первая сторона больше второй на 4 см, а удвоенная длина третьей стороны равна сумме первых двух сторон. Необходимо найти каждую из сторон треугольника.

Обозначим стороны треугольника как a, b и c. Задача представляет собой набор трех условий, для каждого из которых можно сформулировать отдельное уравнение:

a + b + c = 30 (периметр оставляет 30 см)

a = b + 4 (1-ая сторона больше 2-ой на 4 см)

2c = a + b (сумма двух сторон равна удвоенной 3-ей стороне)

В результате получаем систему

Рядом с каждым равенством мы поставили числа (1), (2) и (3). Это делается для удобства записи решения, чтобы можно было ссылаться на выражения. Подобные обозначения часто используются в научной литературе.

Будем решать уравнения способом подстановки. Видно, что в (2) уже выражена переменная a. Подставим (2) в (3):

Нам удалось выразить и переменную c. Теперь подставим (2) и (4) в (1):

В результате нам удалось найти одну из сторон, которую мы принимали за переменную b. Она равна 8 см.

Теперь подставим (5) в (2) то есть выполним обратную подстановку:

Нашли, что вторая сторона треугольника составляет 12 см.

Далее подставим (5) в (4)

Третья сторона оказалась равной 10 см.

В результате получили, что стороны треугольника равны 12, 10 и 8 см. Аналогично решаются системы линейных уравнений с любым количеством переменных. Заметим лишь, что для того, чтобы система имела единственное решение, количество уравнений в ней не должно быть меньше количества переменных. Существуют универсальные алгоритмы (самым известным из них является метод Жордана-Гаусса), позволяющие с помощью компьютера решать системы с тысячами и даже миллионами переменных. Такие задачи могут возникать при расчете прочностей различных строений и деталей машин, моделировании процессов переноса тепла, течения жидкости, протекания электрического тока. Так, на рисунках показаны результаты моделирования столкновения двух автомобилей, а также расчет аэродинамики гоночной машины:

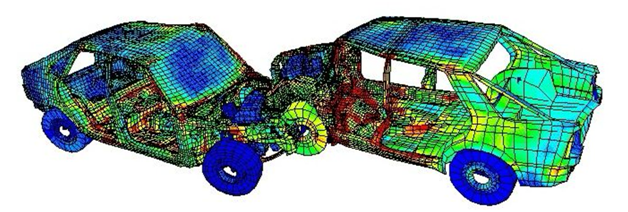Расчет прочности автомобилей при столкновении 

Моделирование воздушных потоков, обтекающих автомобиль 

Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.

Чтобы показать большую практическую значимость решения систем линейных алгебраических уравнений, разберем несколько задач из различных разделов математики, которые сводятся к решению СЛАУ.

Пример.

Представьте дробно рациональное выражение в виде суммы простейших дробей.

Решение.

Очень подробно решение подобных примеров разобрано в разделе разложение дроби на простейшие.

Разложим многочлен, находящийся в знаменателе, на множители (при необходимости смотрите статью разложение многочлена на множители). Очевидно, что x = 0 и x = 1 являются корнями этого многочлена. Частным от деления на является . Таким образом, имеем разложение и исходное выражение примет вид .

Воспользуемся методом неопределенных коэффициентов.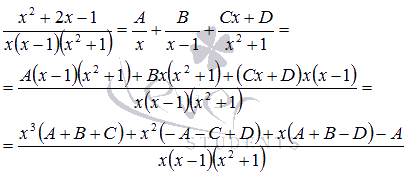

Приравняв соответствующие коэффициенты числителей, приходим к системе линейных алгебраических уравнений . Ее решение даст нам искомые неопределенные коэффициенты А, В, С и D.

Решим систему методом Гаусса:

При обратном ходе метода Гаусса находим D = 0, C = -2, B = 1, A = 1.

Получаем,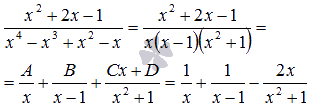

Ответ:

.

Некогда разбираться?