Геометрия

Понимаем геометрию: что это за наука?

Геометрия — это наука, изучающая формы, размеры, расположение и отношения объектов в пространстве. Она включает в себя изучение геометрических фигур, таких как линии, точки, плоскости и тела, а также свойства их отношений.

Геометрия широко используется в нашей жизни, включая области, такие как архитектура, инженерное дело, наука о материалах и промышленность

Она также является важной частью математического образования, включающего в себя изучение геометрических теорем и формул

Геометрия имеет множество практических применений, таких как проектирование зданий и дорог, изучение распределения токов в электрических цепях и оптимизация производственных процессов. Она также помогает в повышении понимания и описания физического мира и помогает разрабатывать лучшие модели понимания мира.

Геометрия дает возможность играть с пространством, экспериментировать, создавать, складывать и формировать новые объекты.
Ее изучение способствует развитию логического мышления, умения решать задачи и приобретения навыков анализа.
Геометрия одна из первых математических наук, изучаемых детьми и является важной частью образования в школе и вузе.

В целом, геометрия является фундаментальной наукой, которая помогает нам понимать окружающий мир и применять эти знания в различных областях нашей жизни. Ее изучение не только полезно, но и увлекательно, и может стать основой для креативных экспериментов и исследований различных явлений.

Что такое геометрия

Когда мы говорим о том, что такое геометрия, мы говорим о той области математики, которая отвечает за изучение размеров, форм и пространственных пропорций фигур, которые определяются ограниченным количеством точек, линий и плоскостей. Эти формы известны как геометрические тела. Понятие геометрии очень полезно для архитектуры, инженерии, астрономии, физики, картографии, механики, баллистики и других дисциплин.

Геометрическое тело — это реальное тело, рассматриваемое только с точки зрения его пространственной протяженности. Идея фигуры является даже более общей, поскольку она также абстрагируется от ее пространственного протяжения, и фигура может иметь много фигур, представляя их «разрезы».

Этимология термина происходит от греческого үɛωμɛτρία, что означает «измерение земли», в свою очередь составленного из ge, что означает «земля»; métron, что означает «меры» или «мера»; и суффикс ía, что означает «качество».

Основные понятия геометрии

Понятие точки

Фигура, которую невозможно измерить, а для вычислений используется только место её расположения, называется точкой. Такие фигуры обозначают цифрами и буквами латиницы. Если точек много, то обозначения должны быть разными.

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

Читается: точка A, точка B, точка C

Понятие линии

Линия представляет собой массу точек. Линии принято обозначать строчными буквами латиницы.

Например:

Линии бывают:

1. Прямые

2. Ломаные

3. Кривые

Часто в геометрии используются прямые линии. Давайте подробнее с ними познакомимся.

По определению, бесконечная линия, не имеющая ограничений, называется прямой. Обозначается маленькими и большими (выбирая 2 любые точки) буквами латиницы.

Например:

Читается: прямая а, прямая AD

Любые две точки на прямой ограничивают геометрическую фигуру – отрезок. Эти точки называются началом и концом отрезка. Фигура обозначается большими буквами латиницы.

Например:                                                                                                               

Читается: отрезок КВ, отрезок АС

Наличие точек дает возможность измерить длину. Длиной отрезка принято считать расстояние между точками, обозначающими начало и конец.

Например:

Расстояние между точками А, В равняется 7 сантиметрам. Считается, что отрезок АВ по длине соответствует 7 сантиметрам.

Записывается следующим образом: АВ=7см

Понятие луча

Рассматривая понятие луч, делаем вывод, что любая точка, лежащая на прямой, делит её на лучи. Сама точка называется началом лучей. Обозначаются большими буквами латиницы.

Например:

Читается: точка В разделяет прямую а на два луча

Чтобы определить нужный луч, на прямую необходимо нанести дополнительные точки.

Например:

Читается: точка А делит прямую с на два луча: луч А, луч АВ

Понятие угла

Геометрическая фигура, состоящая из точки и выходящих из неё двух лучей, называется углом. Лучи называют сторонами угла, а точку – вершиной угла.

Обозначается угол специальным знаком∠, также заглавными буквами латиницы, прописными греческими, цифрами.

Например

Записывается и читается: ∠ВАС (название вершины угла, обязательно записывается в середине) – угол ВАС, ∠β – угол бета

Типы геометрии и их отличительные особенности

Евклидова геометрия является основой классической геометрии и основана на аксиомах греческого математика Евклида. Она изучает пространственные фигуры в двумерном и трехмерном пространстве. Евклидова геометрия применяется в школьной программе и широко используется для анализа и конструирования геометрических объектов.

Нелевитская геометрия, также известная как неевклидова геометрия, нарушает одну или несколько аксиом Евклида. Она изучает геометрические системы, в которых выполняются другие наборы аксиом. Примерами неевклидовой геометрии являются сферическая геометрия и гиперболическая геометрия.

Сферическая геометрия основана на понятиях и свойствах геометрии на сфере. Она имеет особенности, связанные с кривизной поверхности и изменением угловых отношений. Сферическая геометрия находит применение в навигации, астрономии и геодезии.

Гиперболическая геометрия изучает свойства и отношения фигур на поверхности с постоянной отрицательной кривизной. Она имеет отличительные особенности, такие как увеличение углов, параллельные прямые, которые не пересекаются и многие другие непривычные проявления. Гиперболическая геометрия играет важную роль в математике и физике.

Таким образом, разные типы геометрии позволяют нам исследовать и понимать различные аспекты мира и его геометрические свойства. Каждая из геометрий имеет свои применения и может быть использована для решения различных задач с использованием геометрических методов.

Когда изучаются

Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию

В каждом из них немалое внимание уделяется углам:

• В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
• В стереометрии изучаются пространственные углы – двугранные и трехгранные.

Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии

Где обучают в России

В России существует ряд престижных учебных заведений, где можно получить высшее образование в области геометрии и математики.

Вот несколько известных университетов и институтов, предлагающих программы обучения в этой области:

• Московский государственный университет имени М.В. Ломоносова (МГУ): МГУ является одним из ведущих университетов в России и предлагает программы обучения в области математики, включая геометрию. Факультет вычислительной математики и кибернетики предлагает широкий спектр курсов и исследовательских программ.
• Санкт-Петербургский государственный университет (СПбГУ): СПбГУ является одним из старейших и престижных университетов России. Факультет математики и механики предлагает программы по математике и геометрии, включая возможность проводить исследования под руководством опытных преподавателей.
• Новосибирский государственный университет (НГУ): НГУ является ведущим университетом в Сибири и предлагает программы обучения в области математики и фундаментальных наук. Факультет математики и механики имеет различные специализации, включая геометрию.
• Уральский федеральный университет (УрФУ): УрФУ находится в Екатеринбурге и предлагает образовательные программы в области математики и геометрии. Факультет математики и компьютерных наук предоставляет возможность изучения различных аспектов геометрии и применения математических методов в различных областях.
• Казанский (Приволжский) федеральный университет (КФУ): КФУ расположен в Казани и предлагает программы обучения в области математики и естественных наук. Факультет математики и механики предоставляет возможность изучать геометрию и ее приложения.

Это только некоторые из множества учебных заведений в России, где можно получить образование в области геометрии. Выбор университета зависит от ваших предпочтений, академических интересов и географического местоположения.

Углы

Углом называется фигура, образованная двумя полупрямыми, исходящими из одной точки. Эта точка называется вершиной угла, а полупрямые – сторонами угла. Если стороны угла перпендикулярны друг другу, то образуемый ими угол называется прямым (рис. 2,а). Углы меньше прямого называются острыми (рис. 2,б), а углы больше прямого – тупыми (рис. 2,в). Развернутым называется угол, обе стороны которого лежат на одной прямой (рис. 2,г); такой угол равен двум прямым углам. Биссектрисой угла называется прямая, проходящая через его вершину и делящая угол пополам. Углы можно измерять количественно, если определить единицу измерения угла (угол в один градус) как 1/180 развернутого угла. Таким образом, прямой угол содержит 90°, а угол на рис. 2,д содержит больше 180°, но меньше 360°.

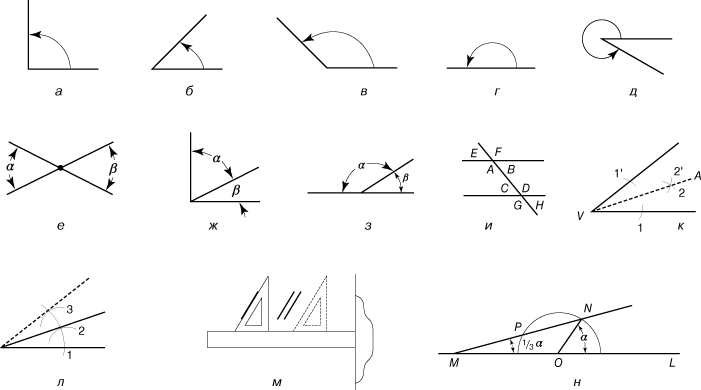
На рис. 2,е, 2,ж, 2,з и 2,и показано, как соотносятся между собой углы некоторых фигур. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого (рис. 2,е). Вертикальные углы равны. Дополнительные углы в сумме составляют 90° (рис. 2,ж), а смежные углы в сумме дают 180° (рис. 2,з). Если прямая пересекает две параллельные прямые, как на рис. 2,и, то углы E, B, C и H равны, и углы F, A, D и G также равны между собой. Углы между параллельными (углы А, В, С, D на рисунке) называются внутренними, а углы, лежащие вне параллельных – внешними. Тот факт, что параллельные образуют с пересекающей их прямой равные углы, используется при вычерчивании параллельных прямых (рис. 2,м).

На рис. 2,к показано, как с помощью циркуля и линейки разделить пополам данный угол: прямая VA – биссектриса угла. На рис. 2,л показано, как удвоить данный угол.

Традиционно в элементарной геометрии выполнялись лишь геометрические построения, которые можно осуществить, используя только циркуль и линейку без делений. Общего подхода к таким построениям не существует, и успех почти целиком зависит от настойчивости и изобретательности. Так, например, может показаться, что задача о разделении угла на три равные части, т.н. трисекция угла, достаточно легка, поскольку сходная с ней задача деления угла пополам решается довольно просто. Однако на протяжении веков все усилия как любителей, так и профессионалов осуществить трисекцию угла неизменно оканчивались неудачей. Правда, эту задачу удалось решить, используя некоторые плоские кривые высших порядков, например, конхоиду и квадратриссу, а Архимед показал, как можно было бы решить задачу о трисекции угла с помощью линейки с двумя отметинами (рис. 2,н). В предложенном им решении задачи на ребре линейки откладывается расстояние МР, равное радиусу ON. Линейка кладется так, чтобы ее край проходил через точку N, тогда точка М попадает на продолжение прямой OL, а точка P – на окружность. Задача о трисекции угла эквивалентна поиску геометрического построения, позволяющего находить корни уравнения x3 – 2 = 0. В 1837 вопрос о трисекции был окончательно решен французским математиком П.Ванцелем, давшим строгое доказательство невозможности точной трисекции угла в общем случае с помощью циркуля и линейки.

Геометрия смежные и похожие науки

Геометрия, как наука о формах и пространственных отношениях, имеет множество смежных и похожих наук, которые исследуют различные аспекты геометрических объектов и их применения.

Вот некоторые из них:

• Алгебра: Алгебра и геометрия тесно связаны и взаимодополняют друг друга. Алгебраические методы используются для решения геометрических задач, а геометрические концепции могут быть выражены в алгебраической форме. Знание алгебры поможет в понимании и анализе геометрических проблем.
• Топология: Топология изучает свойства геометрических объектов, которые не изменяются при непрерывных преобразованиях. Она занимается изучением формы, связности и компактности объектов и позволяет абстрактно анализировать их свойства.
• Математический анализ: Математический анализ включает в себя изучение функций и их свойств, а также предельных значений и непрерывности. Он находит применение в геометрии при изучении кривых, поверхностей и других геометрических объектов.
• Геометрическая оптика: Геометрическая оптика изучает распространение света и его взаимодействие с оптическими системами, такими как линзы и зеркала. Знание геометрии позволяет анализировать и предсказывать свойства и характеристики световых лучей.
• Геодезия: Геодезия занимается измерением и определением геометрических параметров Земли, таких как размеры, форма и положение точек на поверхности Земли. Она находит применение в строительстве, картографии и навигации.
• Дифференциальная геометрия: Дифференциальная геометрия изучает свойства и структуры гладких многообразий. Она находит применение в физике и гравитационной теории, а также в компьютерной графике и робототехнике.
• Компьютерная геометрия: Компьютерная геометрия объединяет геометрию с компьютерными науками и информационными технологиями. Она изучает алгоритмы и методы для анализа и моделирования геометрических объектов на компьютере.

Знание этих смежных и похожих наук поможет более глубоко понять и применять геометрию в различных областях науки, технологий и инженерии.

Треугольники, их виды и признаки их равенства

Сумма углов любого треугольника равна 1800 

Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон

Элементы треугольника:

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)

Биссектриса – это отрезок, делящий угол на два равных угла. Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)

Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)

Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.

Виды треугольников:

У равностороннего треугольника все стороны равны и углы по 600.

У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой. 

У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы

Геометрия в быту и повседневной жизни

Геометрия встречается нам повсюду, начиная от наших домов и мебели. Точные измерения и пропорции влияют на наше зрение и удобство. Для дизайна мебели и интерьерного декора, геометрия играет ключевую роль. Правильные пропорции столов, стульев, кухонных шкафов и диванов не только создают уютный дом, но и увеличивают наше комфортное состояние, уменьшая напряжение и стресс.

Геометрия также является неотъемлемой частью нашей культуры. Круг, квадрат, треугольник, прямоугольник — формы, которые мы видим в живописи, скульптуре, архитектуре, музыке и танцах. Художники и дизайнеры используют геометрические фигуры, чтобы создать формы и структуры, которые вызывают чувство гармонии и красоты.

В нашем повседневном опыте, мы часто используем геометрию, не задумываясь об этом. Например, когда мы нарезаем продукты для приготовления еды, мы используем формы, чтобы обеспечить одинаковый размер. Также мы используем геометрию при навигации по городу — формы знаков и указателей на дорогах и в метро, чтобы нам было проще ориентироваться.

Наконец, геометрия играет важную роль в нашей образовательной системе. Она помогает нам понимать физику и математику, а также развивает наши когнитивные способности и логическое мышление. При изучении геометрии мы учимся анализировать и решать задачи, а также видеть взаимосвязь между различными объектами и формами.

Базовые геометрические объекты

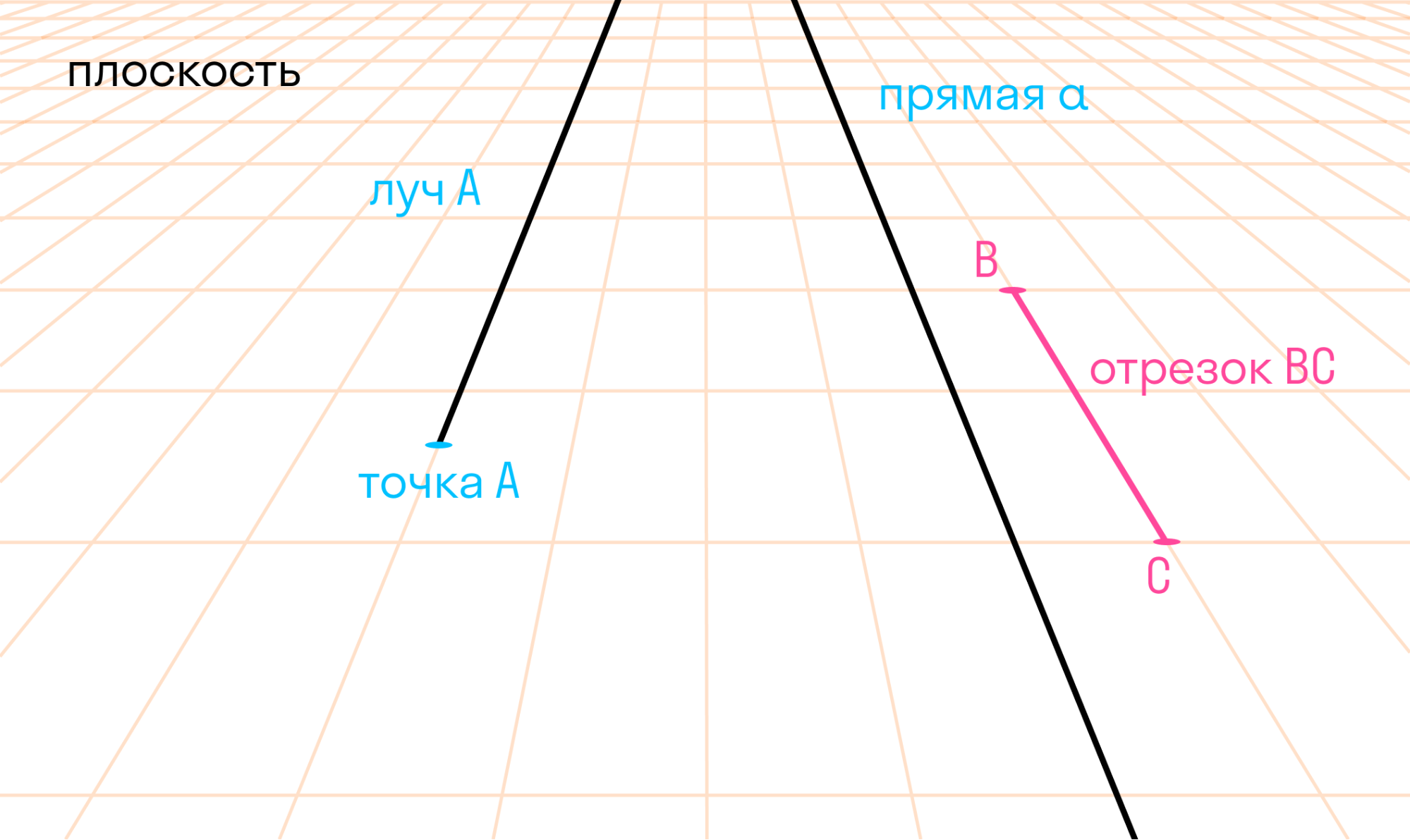
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

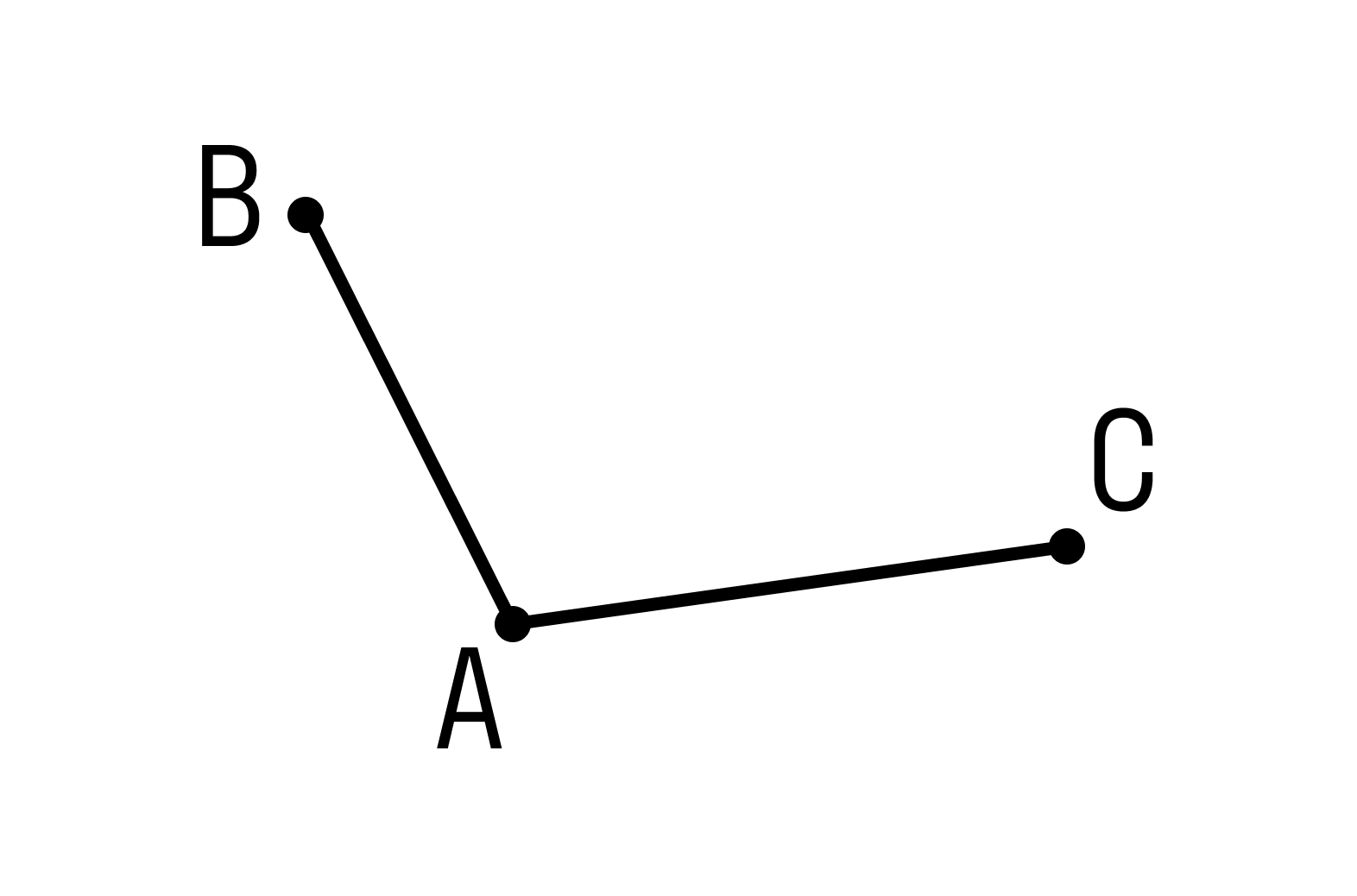
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

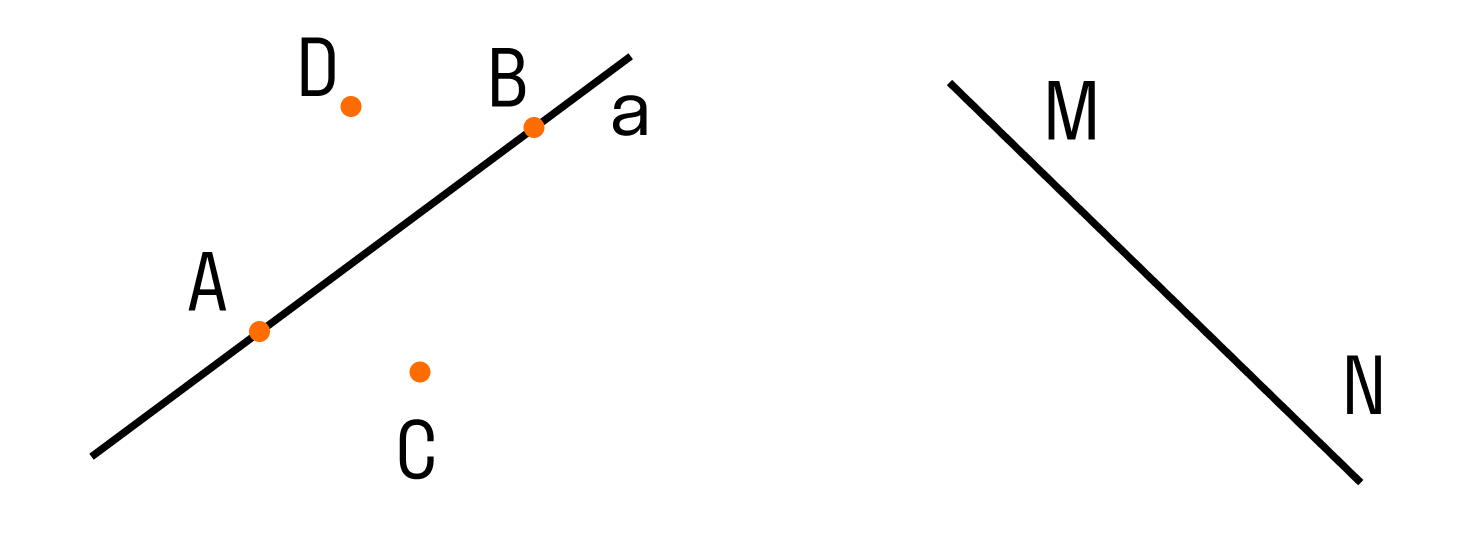
Два варианта расположения точек относительно прямой:

1. Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).

2. Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Важно знать

Через любые две точки можно провести прямую и притом только одну.

Если рассмотреть две прямые, то возможны два варианта их расположения:

1. Прямые пересекаются, то есть имеют одну общую точку.

   Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a пересекается с прямой b в точке O).

   

   

   

   

   

   

   

   

   

   

2. Прямые не пересекаются, то есть не имеют общих точек.

   Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

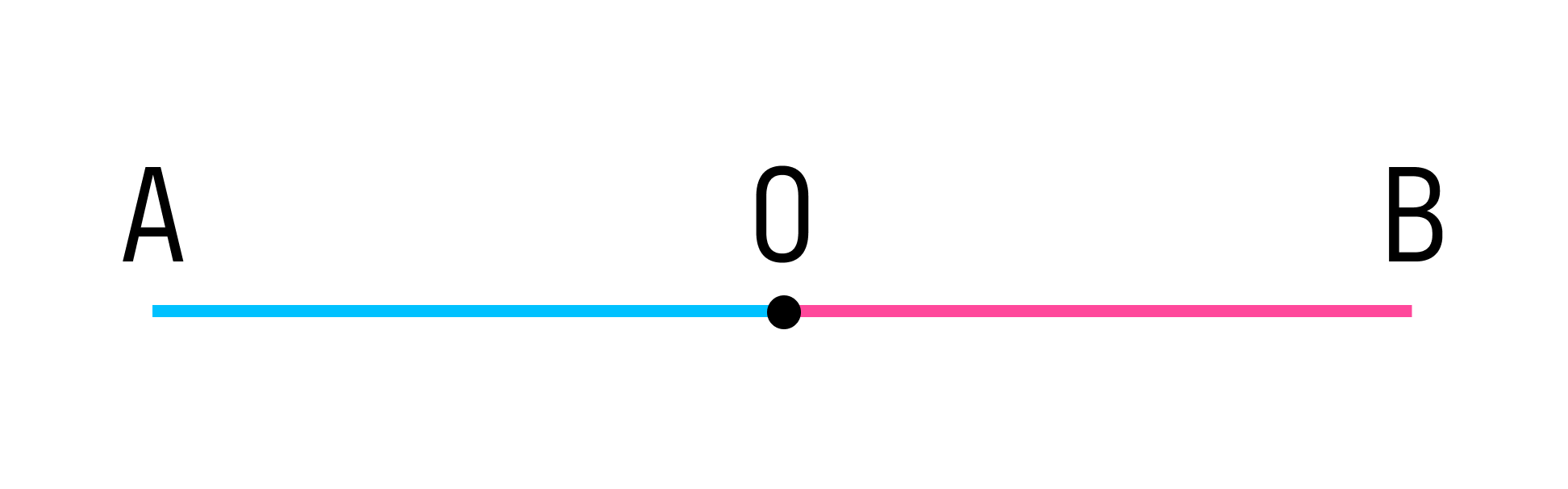
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

• Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.

• Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Основные понятия геометрии

Геометрия – раздел математики, который изучает пространственные фигуры, их свойства и взаимное расположение.

Основными понятиями геометрии являются:

• точка – элементарное понятие, не имеющее размеров;
• линия – бесконечно тонкая и прямая фигура, которая состоит из бесконечного числа точек, лежащих на одной прямой;
• отрезок – часть линии, которая ограничена двумя точками и имеет конечную длину;
• угол – область пространства заключенная между двумя лучами, имеющими общий начальный пункт;
• прямоугольник – четырехугольник, у которого все углы прямые;
• квадрат – прямоугольник, у которого все стороны равны;
• круг – фигура, которая состоит из всех точек, находящихся на одинаковом расстоянии от данной точки, называемой центром круга.

Понимание основных понятий геометрии поможет расширить математические знания и использовать их в таких областях как архитектура, наука, инженерное дело и другие.

Сравнение углов

Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:

\ и \ полностью совмещаются при наложении следовательно: \

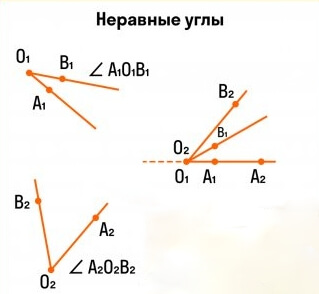
\ и \ не совмещаются при наложении: \

Причем: \

При этом развернутые углы всегда являются равными.

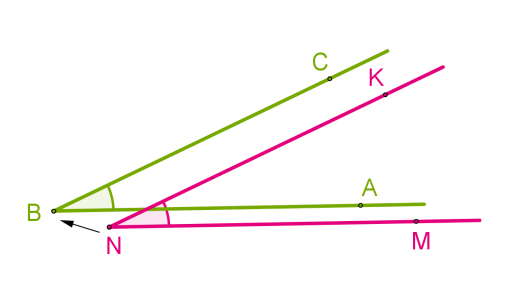
Совмещение углов \ и \ происходит следующим образом:

1. Вершину B одного угла совмещаем с вершиной N другого угла.
2. Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.

Если нет, то один угол — меньше другого: ∠ABC<∠MNK.

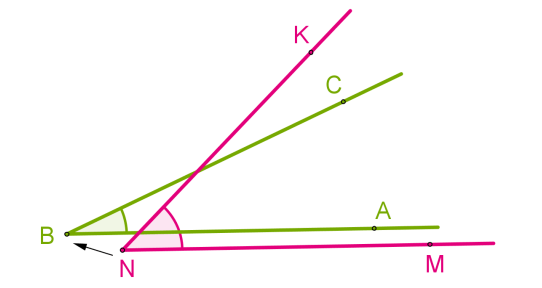
Некоторые важные теоремы, основанные на прямых и углах:

1. Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
2. Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
3. Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
4. Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
5. Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.

В добрый путь!

Далее вы приступаете к изучению планиметрии, ее постулатов и законов. Не гарантируем, что вас ждет простой путь. Однако обещаем, что путь этот будет интересен, полон необычных вещей и восхитительных открытый. Желаем всяческих успехов, друзья.   

{"questions":,"explanations":,"answer":},"speech-33":{"type":"speech","text":"Повторим. Что изучает геометрия? Выберите ниже все подходящие объекты ее изучения."}}},{"content":"<script src=\"https://unpkg.com/@lottiefiles/lottie-player@latest/dist/lottie-player.js\"></script><br /><lottie-player src=\"https://assets9.lottiefiles.com/packages/lf20_ppiv3j5p.json\" background=\"transparent\" speed=\"1\" style=\"max-width: 45%;height: auto;\" loop=\"\" autoplay=\"\"></lottie-player> Чем занимаются планиметрия и стереометрия? Распределите данные разделы геометрии согласно тому, что они в основном изучают. `matcher-26`","widgets":{"matcher-26":{"type":"matcher","labels":,"items":}}}],"mix":1}

Как измерить угол?

Для измерения углов используется транспортир:

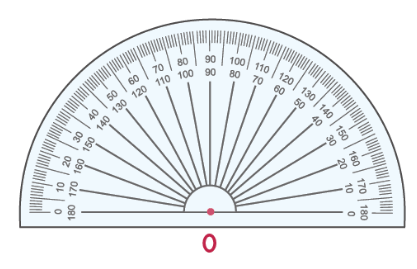Транспортир

Попробуем измерить угол \

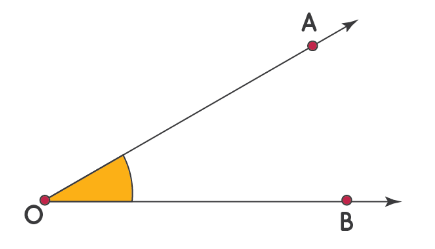
Шаги для измерения угла \.

Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.

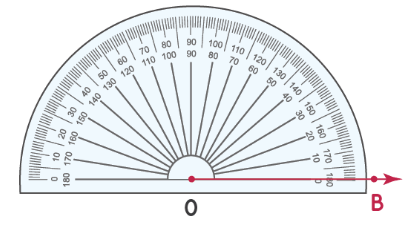
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°

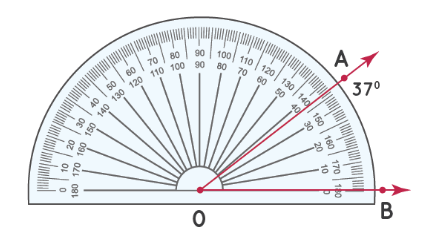
Далее попробуем измерить этот ∠AOC:

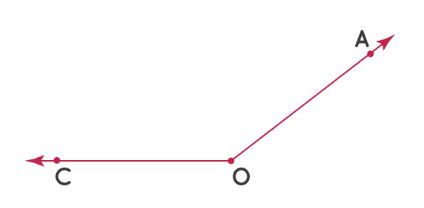
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.

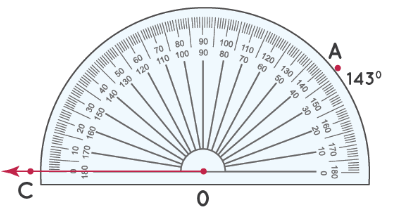
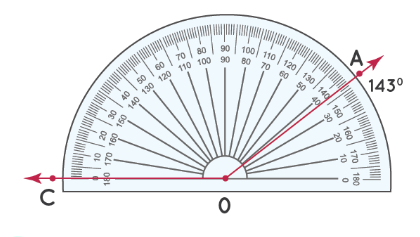
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°

Значение геометрии в образовании

Изучение геометрии позволяет учащимся научиться аргументировать свои рассуждения, строить логические цепочки мысли и решать различные задачи, используя геометрические методы. Такие навыки являются необходимыми во многих сферах жизни, включая инженерию, архитектуру, физику и компьютерные науки.

Геометрия также помогает учащимся развить творческое мышление. В процессе решения геометрических задач, ученики могут использовать различные стратегии и методы, которые помогают им найти нестандартные решения. Это способствует развитию интуиции и креативности учащихся.

Важной особенностью геометрии как предмета в образовании является ее успешная интеграция с другими науками. Геометрические концепции и методы применяются в физике, химии, биологии и многих других дисциплинах

Это позволяет студентам увидеть связь между различными областями знаний и продемонстрировать их практическое применение.

Геометрия также играет важную роль в развитии пространственной интуиции и восприятия. Изучение геометрии позволяет учащимся лучше понимать и интерпретировать информацию, связанную с формами, размерами и относительным расположением объектов. Это важные навыки при работе с графиками, картами, схемами и другими графическими представлениями данных.

Таким образом, геометрия играет значимую роль в образовании, развивая у учащихся аналитическое мышление, логику, творческое мышление и пространственную интуицию. Ее изучение способствует развитию общекультурных навыков и помогает студентам увидеть применимость геометрических концепций в различных науках и практических сферах жизни.

Приложения геометрии в различных областях науки и технологии

Геометрия – это наука о пространственных формах и отношениях между ними. Ее применение находит широкое применение в различных областях науки и технологии.

Архитектура – одна из областей, куда входит геометрия. Архитектурные сооружения разрабатываются с учетом геометрических принципов и пропорций, в основе которых лежат геометрические фигуры – треугольники, круги, прямоугольники и т.д.

Графика – это область, в которой геометрия играет ключевую роль. Все изображения представлены в виде геометрических фигур, что позволяет иметь точный контроль над формой и размером объектов.

Математика и физика – две науки, где геометрия является неотъемлемой частью их изучения. Формулы и уравнения, определяющие пространственные отношения, базируются на геометрии.

Компьютерная графика и анимация – одна из наиболее динамичных областей применения геометрии. Цифровые платформы позволяют создавать более сложные геометрические модели, что открывает новые возможности в визуализации и создании игр, видео и других представлений.

Космология – область, которая изучает пространство и формы, которые оно принимает. Геометрия является важнейшей составляющей физических теорий об изучении космических явлений.

Результаты геометрических наук не могут быть переоценены. Их влияние очень велико и охватывает широкий спектр отраслей жизни, науки и технологии.

Окружность

Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)

Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности

В окружности можно провести радиус, диаметр и хорду

Радиус – расстояние от центра до окружности

Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности

Хорда – прямая, соединяющая две любых точки окружности

Также в окружности есть два вида углов

Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается

Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается

Окружность, вписанная в четырёхугольник

Чтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны

              a + c = b + d

У вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r

Окружность, описанная около четырёхугольника

Чтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:

1. Сумма противоположных углов треугольника равна 180 градусов
2. Вписанные углы, опирающиеся на одну хорду, равны

Окружность, описанная около прямоугольного треугольника

1. Диаметр окружности равен гипотенузе вписанного треугольника
2. Радиус описанной окружности равен половине гипотенузы

R=c/2, где c-диаметр

Детям о науки геометрия

Геометрия — это наука, которая изучает формы, размеры, линии и фигуры. Она помогает нам понять, как все вокруг нас устроено. В геометрии мы изучаем разные геометрические фигуры, такие как треугольники, квадраты, прямоугольники и круги.

Один из первых вопросов, которые возникают в геометрии, — это «Что такое точка?» Точка — это самая маленькая частица, она не имеет размеров, но ее мы можем обозначить небольшой точкой на бумаге.

Затем мы учимся строить линии, которые соединяют точки. Линии могут быть прямыми, изогнутыми или закругленными. Мы также изучаем разные виды углов, такие как прямой угол (90 градусов) и острый угол (меньше 90 градусов).

Фигуры — это особые типы линий, которые образуют закрытые пространства. Например, треугольник имеет три стороны и три угла. Квадрат имеет четыре равные стороны и четыре прямых угла.

В геометрии мы также изучаем свойства фигур. Например, у круга есть радиус — это расстояние от центра круга до любой его точки. Мы также изучаем периметр — это сумма длин всех сторон фигуры, и площадь — это количество пространства, занимаемое фигурой.

Геометрия применяется во многих областях нашей жизни. Например, архитекторы используют геометрию, чтобы строить здания с правильными формами и пропорциями. Математики и инженеры используют геометрию для решения сложных задач и создания новых технологий.

Изучение геометрии помогает нам развивать логическое мышление, улучшать навыки решения задач и применять знания в повседневной жизни. Открывай новые фигуры, исследуй их свойства и познавай удивительный мир геометрии!