Проценты, процент от числа

Формула для расчёта сложного процента

Для того чтобы рассчитать сумму которая будет накоплена на вашем счете за несколько лет с капитализацией процентов раз в год, следует воспользоваться этой формулой:

А вот формула для вклада с ежемесячной капитализацией процентов:

Давайте сравним два вклада на одинаковые суммы, сроки и процентные ставки, но один из них будет с ежегодной, а второй – с ежемесячной капитализацией процентов.

Пускай сумма вклада будет составлять 50000 рублей, процент годовых – 15%, а срок инвестирования – 20 лет. Тогда в первом случае мы получим:

50000х(1+0,15)20=818326,86 рублей

А во втором случае:

50000х(1+0,15/12)240=985774,67 рублей

Теперь предположим, что срок инвестирования будет составлять уже 50 лет, тогда при ежегодной капитализации итоговая сумма составит:

50000х(1+0,15)50=54182872,07 рублей

А при ежемесячной капитализации:

50000х(1+0,15/12)600=86295696,10 рублей

Очевидно, что во втором случае сложный процент работает куда более эффективно, ведь по факту начисление процента на процент происходит в 12 раз чаще. И хотя годовой процент одинаков для обоих случаев, во втором из них мы получаем несколько большую прибыль.

Обратите внимание на то, что при увеличении срока инвестирования в два с половиной раза (50/20=2.5), итоговая прибыль возросла аж в 66 раз. К слову, если бы вы забирали полученные проценты по вкладу, а не реинвестировали их как в примерах выше (то есть не использовали бы то преимущество, которое даёт сложный процент), то за пятьдесят лет сумма вашего вклада составила бы всего 425000 рублей (ежегодный процент в размере 50000х1.15=7500 рублей, умноженный на 50 лет, плюс первоначальная сумма вклада)

К слову, если бы вы забирали полученные проценты по вкладу, а не реинвестировали их как в примерах выше (то есть не использовали бы то преимущество, которое даёт сложный процент), то за пятьдесят лет сумма вашего вклада составила бы всего 425000 рублей (ежегодный процент в размере 50000х1.15=7500 рублей, умноженный на 50 лет, плюс первоначальная сумма вклада).

Пятьдесят четыре миллиона (при ежегодной капитализации) или восемьдесят шесть миллионов (при ежемесячной капитализации), против четырехсот тысяч (без реинвестирования), вот вам и наглядная иллюстрация сложного процента в действии.

Вы можете поделиться этой статьёй на своей странице в соцсетях:

Словарь трейдера

olegas ›

Торгую га финансовых рынках с 2008 года. Сначала это был FOREX, затем фондовая биржа. Сначала занимался преимущественно трейдингом (краткосрочными спекуляциями на валютных рынках), но сейчас все больше склоняюсь к долгосрочным инвестициям на фондовом рынке. Хотя иногда, дабы не терять форму и держать себя в тонусе, балуюсь спекуляциями на срочном рынке (фьючерсы, опционы). Пишу статьи на сайт ради удовольствия.

Что такое процент?

В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% = = 0,01

Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% = = 0,02

Простой расчет сложных процентов

Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль – 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.

Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Чем сложный процент отличается от простого

Простой процент означает, что вы получаете доход на начальную сумму вклада в конце срока размещения. Если вы вложили 100 000 рублей на один год под 10%, то в конце этого срока вам начислят 10 000 рублей в виде процентов. Эти 10 000 не плюсуют к сумме вклада в течение года, а перечисляют единоразово в конце срока. Если вы продлеваете вклад (допустим, банк все еще предлагает такую ставку), то изначальная сумма остается той же — 100 000 рублей — и проценты в конце следующего года составят те же 10 000. Таким образом, за два года вы получите 20 000 рублей в виде дохода.

При сложном проценте вы получаете доход на весь остаток, который есть на счету на определенную дату: например, конец месяца, квартала или года. Период, за который банк начисляет проценты на весь остаток, называется сроком капитализации. При этом считают общую сумму вклада со всеми пополнениями, а при следующем начислении — еще и начисленные проценты. То есть, если вы сделали вклад на сумму 100 000 рублей под 10%, а в течение года положили еще 100 000, то в конце года получите 20 000 рублей в виде процентов. А в следующий раз, если сумма и ставка не менялись — уже 22 000 рублей.

Часто задаваемые вопросы

Как рассчитать сложный процент?

Если не использовать формулу, то посчитайте сколько вы получите по вкладу за один год, а затем возьмите полученную сумму и посчитайте процент по вкладу с ней, а не с начальной суммой. То есть используйте одну и ту же процентную ставку, но разные суммы (сначала за первый год, потом за второй и так далее).

Общая формула, если процент начисляется ежегодно: , где – ваша начальная сумма, – годовая ставка, – количество лет.

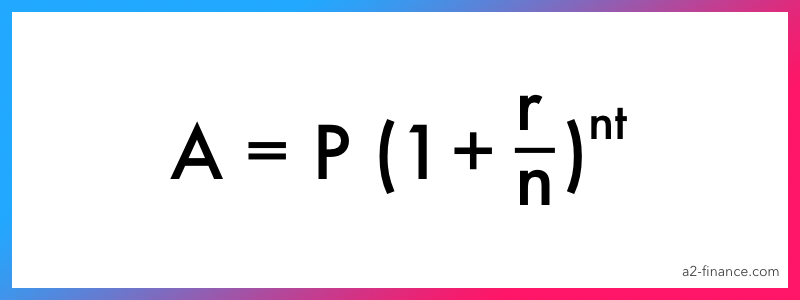
Когда нужно использовать сложные проценты?

Если вы вкладываете деньги, например, открывая депозит в банке, то сложные проценты помогут узнать, какую сумму вы получите в конце вклада.

Если оформляете заём, то сложный процент поможет узнать величину долга в конце всего периода займа.

Какая формула сложного процента?

Обычная формула выглядит так: , где – начальная сумма, – годовая ставка, – количество периодов начисления ставки, – общий срок вклада в годах.

Почему сложные проценты предпочтительнее простых процентов?

Основная причина в том, что при использовании сложных процентов – в конце срока вложения, вы получите больше денег, чем при использовании простого процента. Это главное преимущество.

Какие факторы влияют на расчёт сложных процентов?

Их четыре:

начальная сумма, т.е. та, которую вы вкладываете, или с которой открываете депозит;
пополнения, т.е. сумма, которую вносите и периодичность, с которой пополняете;
ставка – это процент, начисляемый ежегодно на весь период открытия вклада или инвестирования;
срок инвестирования, т.е. период, в течение которого будет открыт вклад, чаще всего используется в годах, но иногда применяются месяцы или даже дни.

8. Формула сложных процентов если процентная ставка дана не в годовом исчислении

Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула расчета сложных процентов выглядит так:

S = K * ( 1 + P/100 )N

Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — процентная ставка,
N — количество периодов начисления процентов.

Формула расчета процентов на вклад:

Sp = S — K

или

Sp = K * ( 1 + P/100 )N — K

Иногда удобнее использовать формулу расчета в таком виде:

Sp = K * (( 1 + P/100 )N — 1)

Пример 8.1 Принят депозит 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5% в месяц.

S = 100000 * (1 + 1.5/100)3 = 104 567.84
Sp = 100000 * ((1 + 1.5/100)3 — 1) = 4 567.84

Онлайн калькулятор
Расчет вклада с процентами

По теме страницы

Список таблиц финансовых расчетовФормулы расчета процентов по вкладуФормулы расчета сложных процентов и выбор вкладаФормулы расчета НДС, сумма с НДС, сумма без НДС, выделение НДСФормула расчета кредита. Аннуитет, аннуитетные платежи, коэфициент аннуитета, формула аннуитетных платежейФормула финансового рычага (финансового левериджа)ДисконтированиеКарта сайта — Подробное оглавление сайта

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

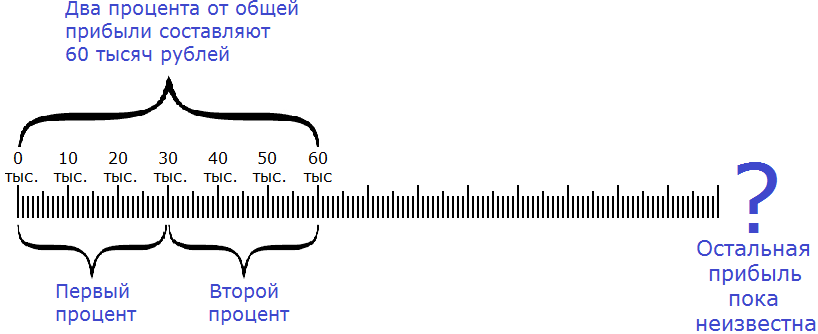
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Сложные проценты в инвестиционной деятельности и спекулятивной торговле

Рассмотрим, как работает схема сложных процентов на дивидендах по акциям. Допустим, были приобретены акции на 100 000 рублей. Их постоянная дивидендная доходность составляет 5% в год. Все полученные средства сразу реинвестируется в те же акции (это значит, что производится дозакупка акций на полученную сумму). Спустя 10 лет доход, полученный за счет этих дополнительных вложений, составит 63000 рублей, а спустя 20 лет – уже 165 000 рублей. Если продолжать действовать в таком же режиме на протяжении 30 лет, то дивидендная прибыль составит уже 332 000 рублей (или 332% от первоначального вложения). Если трейдер будет тратить дивиденды на другие нужды, то будет иметь место схема простого процента, и заработок за 30 лет составит всего 150% — это в 2,2 раза меньше, чем в схеме сложных процентов.

Возникновение этой разницы обусловлено тем, что на основе реинвестированных доходов в будущем формируются новые поступления дивидендов. При этом происходит срабатывание эффекта «снежного кома». На каждый год дивиденды, которые выплачиваются на реинвестированные доходы, возрастают быстрее и быстрее. Нужно понимать, что чем больше частота дивидендных выплат, тем ярче проявляется описанный эффект.

Аналогичный эффект наблюдается и по облигациям. Если средства инвестируются в купонные облигации, предусматривающие выплату купона (определенного процента) через установленные временные промежутки, то возможностью для трейдера увеличить заработок выступает реинвестирование купонного дохода. Схема получения процентных доходов аналогична случаю с начислением дивидендов. Если выплата купона производится ежемесячно, эффект прогрессирующего дохода будет более ярко выражен, чем в случае с годовыми выплатами.

Еще один вариант применения сложных процентов – работа с фьючерсами. Рассмотрим пример:

в текущий момент рыночная цена фьючерса составляет 160 000 рублей,
сумма гарантийного обеспечения по фьючерсу составляет 20 000 рублей,
у трейдера есть 45 000 рублей, на которые он приобретает 2 фьючерса под гарантийное обеспечение, составляющее 40 000 рублей,
проходит две недели. Рост цены составил 5%. Зачисляется доход – вариационная маржа в сумме 16000 рублей,
трейдер может докупить еще один фьючерс (за счет остатка собственных средств в 5000 рублей и полученной вариационной маржи),
проходит еще три недели. Цена возрастает еще на 5%. Вариационная маржа составит 25200 рублей, из которых 8400 рублей приходится на последний докупленный фьючерс.

Однако для спекулятивной торговли достижение эффекта сложных процентов возможно только в том случае, если динамика по базовому активу непрерывно растущая (или непрерывно падающая для продаваемых фьючерсов). Удержание позиций на все деньги отличается высокими рисками, если цена меняется в неблагоприятном направлении.

Посчитать самостоятельно

Все же изучение уже посчитанных таблиц или использование шаблонов с готовыми формулами не настолько наглядно. Предлагаю пощупать «сложный процент» руками: взять калькулятор в руки, вбить доступную для инвестиций сумму и умножить ее на 1,1 (рост на 10%) для первого года; умножить полученную сумму на тот же коэффициент для второго года и так далее до желаемого срока.

Подсчет сложного процента на калькуляторе на 5 лет

Формула сложного процента выглядит так:

SUM = X × (1 + %)n, где:

SUM — конечная сумма;

X — начальная сумма;

% — процентная ставка, процентов годовых ÷ 100;

n — количество периодов, лет (месяцев, кварталов).

Пример 1

Вы положили один миллион рублей на 5 лет и ожидаете 10% годовых. Какая сумма будет у вас в конце срока? Рассчитаем по формуле сложного процента:

SUM = 1 000 000 × (1 + 10 ÷ 100)5 = 1 610 510 рублей.

Что такое процент?

Процентом является одна сотая часть

Например,

Еще пример,

Проценты встречались настолько часто, что люди заменили дробь

Эта запись читается как «один процент». Она заменяет собой дробь

1% =

Три типа задач на проценты

Для всех видов практических задач на проценты используется универсальная формула:

p=(A/B)x100%;

где р — процент, который число А составляет от числа В. (1).

Величину р следует трактовать здесь как количество сотых долей, которые число, А составляет от числа В. Пользуясь этой формулой, можно решать три типа задач, по числу неизвестных в ней.

Задачи первого типа

Здесь необходимо найти неизвестное число процентов. Для этого используется формула (1). Вот простейший пример: сколько % от 25 составляет число 12,5?

Решение: p=(12,5/25)x100%=50%.

Задачи второго типа

Нужно найти, сколько будет р % от числа В. Из (1) можно легко получить следующую формулу:

А=(р/100)xВ. (2).

Задача. Сколько будет 13% от 6700 рублей?

Решение: А=(13/100)x6700=871 рубль.

Задачи третьего типа

Если известно, что р % от числа В равно А. Чему равно В? Из (1) следует, что

В=(100xА)/р. (3).

Задача. 7% от некоторого числа равно 777. Чему равно само число?

Решение: В=(100×777)/7=11100.

Нахождения числа по его проценту

60 000 : 2 = 30 000

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

35 : 7 = 5

5 × 100 = 500

Что такое процент?

Что такое процент? Как его определить? Как считать проценты? Получить ответы на эти и многие другие вопросы, можно рассмотрев данный урок.

Рассмотрим ситуацию.

В зоопарк привезли сто килограммов овощей. Порция каждого питомца составила один килограмм. Какая часть овощей досталась одному жителю зоопарка?

Чтобы ответить на поставленный вопрос, давайте вспомним тему «Дроби», а именно, определение числителя и знаменателя:

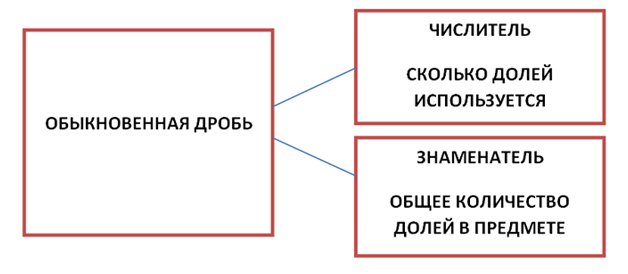
Мы знаем, что всего привезли 100 килограммов овощей, а одно животное получило 1 килограмм. Исходя из рассмотренного определения, делаем вывод, что общее количество долей –100 записываем в знаменатель, а число используемых долей для одного животного –1 ставим в числитель. Запишем полученную дробь:

1 100 или 0,01 часть овощей досталась каждому питомцу зоопарка.

Использовать дроби, такого вида, в повседневной жизни не всегда удобно, для краткой записи и удобства вычислений существует специальное понятие:

Процент — одна сотая часть чего-либо. Для обозначения процента существует специальный символ — %

Для письменного обозначения процента сначала записываем цифру, обозначающую необходимое количество, а рядом ставим символ %.

Произносится:

15% – пятнадцать процентов

83% – восемьдесят три процента

49% – сорок девять процентов

Опираясь на определение процента, можно сказать, что каждый житель зоопарка получил 1% овощей, от привезенного количества.

Важно! Одна сотая часть всегда равна одному проценту!

Главное запомнить, что одна сотая часть это 1%!

Нахождение процента от числа

Рассмотрим пример.

В летний оздоровительный лагерь заехало 4500 детей. 20% от общего количества приехали сразу на 2 лагерные смены. Сколько детей приехали на две смены?

Чтобы найти количество детей, заехавших в лагерь сразу на 2 смены, нужно определить численность человек, соответствующую 20% от общего количества.

Это можно сделать несколькими способами, которые мы сейчас и рассмотрим.

1 способ

Нам известно общее количество детей –4500, от этого количества нужно найти число соответствующее 20%. Всех заехавших детей принимаем за 100%:

4500=100%.

Теперь можно узнать, чему равен 1%. Для этого

4500:100=45.

Получается, что число 45 соответствует 1%:

1%=45.

1% соответствует число 45, а какое же число соответствует 20%? Для ответа на этот вопрос, необходимо числовое значение соответствующее 1%, повторить 20 раз, то есть:

45×20=900.

Запишем решение данной задачи с использованием 1 способа:

Решение.

1) 4500:100=45(д) – число детей, соответствующее 1%;
2) 45×20=900(д) – заехали на 2 смены.

Получается, что на две смены приехали 900 человек, что соответствует 20% от общего количества заехавших детей.

Запомни!

Чтобы найти процент от числа:1. Делим число на 100;2. Полученное число умножаем на количество искомых процентов

2 способ

Если же вычисления с использованием 1 способа вызвали у вас трудности, то можно воспользоваться 2 способом, который заключается в применении правила:

Чтобы найти процент от числа:1. Умножаем данное число на количество искомых процентов;2. Полученное произведение делим на 100

Зная, число заехавших детей и количество искомых процентов, можем воспользоваться рассмотренным правилом. Вначале, находим произведение числа (4500) и искомых процентов(20%):

4500×20=90000.

Следуя правилу, нам нужно разделить полученное произведение на 100.

90000:100=900.

Запишем решение задачи с использованием 2 способа:

Решение

1)4500×20=90000

2)90000:100=900(д) – приехали на 2 смены.

Получается, что 900 человек приехали на две смены.

Разберем еще один пример, где описано, как посчитать процент от числа?

Например: надо найди 25% от числа 50.

Для выполнения задания, необходимо выбрать способ, которым вычислять будет удобнее. При использовании первого способа нужно будет делить число 50 на 100, что не совсем удобно. В этом случае проще применить второй способ. Используя рассмотренное правило, сначала умножаем известное число (50) на количество процентов(25):

Получаем,

50×25=1250.

Теперь, полученное произведение нужно разделить на 100. Для этого вспомним правило деления натурального числа на 100:

Чтобы разделить число на 100, достаточно отбросить (отделить запятой) справа 2 цифры500:100=5, 345:100=3.45, 15:100=0.15

Используя правило, делим 1250 на 100:

1250:100=12,5.

Мы выяснили, что 25% от числа 50 равно 12,5.

Мы рассмотрели 2 способа нахождения процента от числа. И только вы сами сможете выбрать подходящий именно вам способ для решения той или иной арифметической задачи!

Простые и сложные %

Рассмотрим ещё тип задач, относящихся к финансовым и связанных с процентами. Это такие задачи, в которых нужно вычислять доход от вклада или инвестиций. Вот такой пример. Вы вложили деньги в банк под р % годовых некую сумму S0. Чему будет равен ваш капитал через n лет? И ответ на этот вопрос зависит от того, какой у вас вклад: с простым начислением процентов или с их капитализацией.

Простое начисление процентов — это ежегодное (ежеквартальное, ежемесячное) получение р % от суммы вашего вклада, когда начальная сумма вклада S0 фиксирована, а вы регулярно с этой суммы получаете фиксированный доход, то есть каждый год (квартал, месяц) вы получаете прибыль 0,01p•S0. Через n лет ваша прибыль станет равна 0,01nр•S0. Полученная прибыль суммируется с вашим начальным вкладом S0, в результате чего вся сумма прибыли вместе с процентами составит:

S=S0•(1+0,01np). (4).

Задача. Вы положили 100000 рублей в банк под 10% годовых на 5 лет. Чему станет равен ваш вклад?

Решение: S=100000•(1+0,01•5•10)=100000•1,5=150000 рублей.

Допустим теперь, что ваш вклад с капитализацией процентов. Это означает, что после каждого начисления проценты прибавляются к уже имеющейся сумме на вашем счету. Таким образом, после следующего начисления сумма процентов становится больше. Например, в первый год проценты по вкладу с капитализацией составят 0,01р•S0, а за второй год эта сумма будет уже больше и составит 0,01p•(S0+0,01p•S0)=0,01p•S0•(1+0,01р), а за третий год — 0,01p•(S0+0,01p•S0•(1+0,01р))=0,01р•S0•(1+0,01p+(0,01p)²).

Выражение в скобках представляет собой сумму геометрической прогрессии, которая равна (0,01р)². Поэтому за третий год сумма на вашем счету станет равной S0+S0•(0,01р)³. Продолжая так дальше, через n лет или периодов начисления, сумма на счету вместе с начисленными процентами составит:

S=S0•(1+0,01р)ⁿ. (5).

Мы получили так называемую формулу сложных процентов, которая позволяет высчитывать сумму на вашем счету по вкладу с капитализацией процентов.

Задача. Вы положили всё те же 100 000 рублей на 5 лет под 10 % годовых, но открыли вклад с капитализацией. Сколько к концу указанного срока будет на вашем счету?

Решение. Пользуясь формулой сложных процентов, получим: S=100000•(1+0,01•10)^5=100000•1,1^5=100000•1,61051=161051 рубль.

Сравнивая результаты, полученные по формулам (4) и (5), видим, что по вкладу с капитализацией сумма на счету стала больше на 11051 рубль по сравнению с обычным вкладом, где происходит простое начисление процентов. Таким образом, второй способ вложения денег выгоднее.

Как найти 2 3 от 100

Вычисление доли числа может быть сложной задачей, особенно если мы имеем дело с дробными числами. В данной статье мы поговорим о нахождении 2/3 от числа и предоставим вам несколько простых и эффективных способов решения этой задачи.

Что такое дробь

Для начала, давайте разберемся, что такое дробь. Дробь — это число, состоящее из одной или более частей единицы. У дроби есть две основные части: числитель и знаменатель. Числитель указывает, сколько частей взяли, а знаменатель показывает, на сколько частей разделена единица.

Как найти 2/3 от числа

Для того чтобы найти 2/3 от числа, мы можем использовать следующую формулу:

Например, чтобы найти 2/3 от числа 18, мы должны разделить 18 на 3, а затем умножить результат на 2:

Таким образом, 2/3 от числа 18 равно 12.

Примеры вычисления

Давайте рассмотрим еще несколько примеров вычисления 2/3 от чисел:

Найти 2/3 от числа 120:

2/3 * 120 = (2 * 120) / 3 = 240 / 3 = 80

Таким образом, 2/3 от числа 120 равно 80.

Найти 2/3 от числа 30:

Для начала, мы можем составить пропорцию:

Здесь мы ищем значение x, которое является 2/3 от числа 30.

Решим эту пропорцию:

Таким образом, 2/3 от числа 30 равно 20.

Выводы и полезные советы

Чтобы найти 2/3 отчисла, умножьте число на 2/3.
Вы также можете использовать пропорцию для решения этой задачи.
Если вы хотите преобразовать 2/3 в десятичную дробь, разделите числитель на знаменатель. В этом случае, 2/3 = 2 : 3 = 0.6666666666667.

Надеемся, что эта статья была полезной для вас и помогла разобраться в том, как найти 2/3 от числа. Применяйте эти простые методы, и математика станет намного проще!

Как найти одного числа от другого

Для того чтобы найти процентное отношение одного числа к другому, нужно число, которое нам дано, разделить на другое число и умножить его на 100%. Например, для вычисления процентного отношения числа 12 к числу 30, мы должны разделить 12 на 30 и умножить результат на 100%. Получается, что 12 составляет 40% от числа 30. Это означает, что если мы возьмем 30 и разделим его на 100 частей, то 12 из этих частей будут составлять число 30. Таким образом, процентное отношение позволяет нам определить, насколько одно число больше или меньше другого.

Как узнать к какому числу прибавили процент

Чтобы узнать, к какому числу был прибавлен процент, следует выполнить следующие шаги. Во-первых, нужно прибавить этот процент к изначальному числу. Затем необходимо разделить полученную сумму на 100% плюс процент, который был прибавлен. Получившееся значение будет искомым числом. Например, если у нас есть число 100, и нам известно, что к нему был прибавлен 10%, то мы прибавляем 10 к 100, получаем 110. Затем делим 110 на 110% (100% + 10%), что равно 100, и умножаем на 10%. Получаем 10. Таким образом, к числу 100 был прибавлен процент в размере 10.

Как найти 3 7 от числа 28

Чтобы найти 3/7 от числа 28, нужно умножить это число на 3/7. Для этого можно сначала вычислить десятичную дробь 3/7, которая равна примерно 0,4286. Теперь умножаем 28 на 0,4286 и получаем примерно 12. Таким образом, 3/7 от числа 28 равно 12. Точно также можно найти 9/14 от числа 28. Десятичная дробь 9/14 равна примерно 0,6429. Умножаем 28 на 0,6429 и получаем примерно 18. Итак, 9/14 от числа 28 равно 18. Третий пример — 19/28 от числа 28. Здесь десятичная дробь равна примерно 0,6786. Умножаем 28 на 0,6786 и получаем примерно 19. Таким образом, 19/28 от числа 28 равно 19.

Как найти какую часть составляет число от числа

Например, если нам нужно найти, какую часть 20 составляет от числа 100, мы делим 20 на 100. Получаем результат: 0,2. Это означает, что число 20 составляет 0,2 или 20% от числа 100.

Если нам нужно найти, какую часть составляет число 3 от числа 9, мы делим 3 на 9. Результат равен 0,33333. (бесконечная десятичная дробь). Это означает, что число 3 составляет примерно 0,33333. или 33,33. % от числа 9.

Таким образом, чтобы найти часть, которую одно число составляет от другого, мы делим первое число на второе и умножаем на 100, чтобы получить результат в процентах.

Для нахождения 2/3 от 100 необходимо разделить числитель (2) на знаменатель (3) и затем умножить полученное значение на 100. В данном случае, результатом такого преобразования будет 0,666(6). Получившееся число является десятичной дробью, которую можно представить в виде бесконечной периодической десятичной дроби. В данном случае, цифра 6 будет повторяться бесконечно после запятой. Если нужно представить результат в виде процентов, мы можем умножить значение на 100. Таким образом, 2/3 от 100 равно примерно 66,67%

Важно отметить, что при округлении такого значения, возможны некоторые погрешности, так как периодическая дробь не может быть точно представлена с помощью конечного числа знаков

Проверь себя

Задание 1.Найдите 26% от числа 380.

100
98,8
281,2
26

Задание 2. Известно, что 100 – это 20% от какого-то числа. Найдите это число.

Задание 3. Магазин перед праздниками сделал скидку 11% на всю технику. В результате мультиварка стала стоить 3560 рублей. Сколько стоила мультиварка до скидок?

4000
3168,4
3951,6
4100

Задание 4. Что такое сложный процент?

Это процент, выраженный нецелым числом;
Это процент, который со временем начисляется не только на изначальную сумму, но и на те проценты, которые были начислены до этого.
Это процент, который большее 100;
Ни один из приведенных выше вариантов.

Задание 5. Число 200 уменьшили на 30%, а после этого полученный результат увеличили на 30%. Какое число получилось?

Ответы: 1. – 2 2. – 4 3. – 1 4. – 2 5. – 2

Заключение

Даже спустя сотни лет после открытия, сложные проценты не теряют своей популярности и значимости. Это мощный инструмент в финансовом мире для приумножения капитала. Не имеет значения являетесь вы крупным инвестором или просто держите депозитный счет в банке. Более важным будет ваше мастерство находить самые выгодные предложения.

Согласитесь, ведь куда лучше сделать вклад с меньшей процентной ставкой, но с возможностью капитализации доходов. Чем положить деньги с высокой ставкой, но без такого преимущества.

Алексей

Активно инвестирую в высокодоходные, перспективные направления. Делюсь опытом и рассказываю про актуальные варианты заработка.

Формула для расчёта сложного процента

Что такое процент?

Простой расчет сложных процентов

Задания для самостоятельного решения

Чем сложный процент отличается от простого

Похожие калькуляторы

Часто задаваемые вопросы

Как рассчитать сложный процент?

Когда нужно использовать сложные проценты?

Какая формула сложного процента?

Почему сложные проценты предпочтительнее простых процентов?

Какие факторы влияют на расчёт сложных процентов?

8. Формула сложных процентов если процентная ставка дана не в годовом исчислении

Онлайн калькулятор Расчет вклада с процентами

По теме страницы

Нахождения числа по его проценту

Сложные проценты в инвестиционной деятельности и спекулятивной торговле

Посчитать самостоятельно

Что такое процент?

Три типа задач на проценты

Задачи первого типа

Задачи второго типа

Задачи третьего типа

Нахождения числа по его проценту

Что такое процент?

Нахождение процента от числа

1 способ

2 способ

Простые и сложные %

Как найти 2 3 от 100

Что такое дробь

Как найти 2/3 от числа

Примеры вычисления

Выводы и полезные советы

Как найти одного числа от другого

Как узнать к какому числу прибавили процент

Как найти 3 7 от числа 28

Как найти какую часть составляет число от числа

Проверь себя

Заключение

Алексей

Похожие записи:

Похожие записи:

Онлайн калькулятор
Расчет вклада с процентами