Обращение десятичной дроби в простую и обратно

Дробь с целым числом

Необходимо рассмотреть и другие примеры, с повышенной сложностью. Стоит взять 2,25. Как и до этого, для начала, лучше всего правильно обозначить название дроби. В этот раз имеется две целых, двадцать пять сотых. В связи с тем, что после знака находится две цифры, то они являются сотыми.

Как десятичную дробь перевести в обыкновенную дробь:

• Нецелая часть записывается в виде 25/100.
• Осталось дописать две целых. Они ставятся в начало, и таким образом получается смешанная дробь.
  
• 25/100 можно сократить. Для простоты, реально начинать с деления на 5, но неплохо сразу воспользоваться числом 25. В результате сокращения получается ¼.
• Остается лишь подписать две целые к ¼. Результат – 2 ¼.

Наконец, стоит рассмотреть и процесс работы с тысячными. Для разбора возьмем 4,112. Вновь работу нужно начать с верного прочтения. Получится четыре целых, сто двенадцать тысячных. Без труда удастся выделить первую цифру, 4, а затем подставить к ней сто двенадцать тысячных. Они выглядят так – 112/100.

Остается лишь сократить, чтобы придать лучший вид. В этом конкретном примере общим делителем является шесть. Результат – простая дробь 4 14/125.

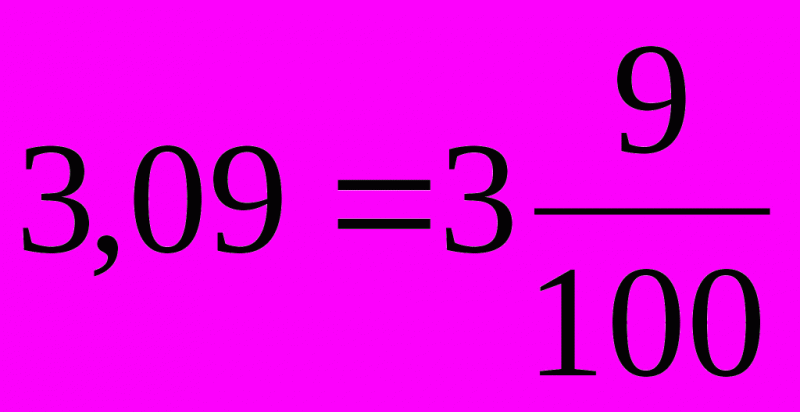
Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Перевод из восьмеричной системы в двоичную

Способ 1:

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Возьмем число 43₈.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 100011₂

Способ 2:

Используем таблицу триад:

Цифра	1	2	3	4	5	6	7
Триада	000	001	010	011	100	101	110	111

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

351₈ = (011) (101) (001) = 011101001₂ = 11101001₂

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

1% = 1/100 = 0,01

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Быстрая напоминалка:

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Ответ: 5,4 = 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

Как решаем:

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Как перевести обычную дробь в десятичную

Прежде чем мы научимся переходить с обычного на десятичное представление, давайте вспомним различия между двумя типами дробей и сформулируем важное правило. Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42

А вот так выглядят те же числа в виде правильных дробей:

Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А вот так выглядят те же числа в виде правильных дробей:

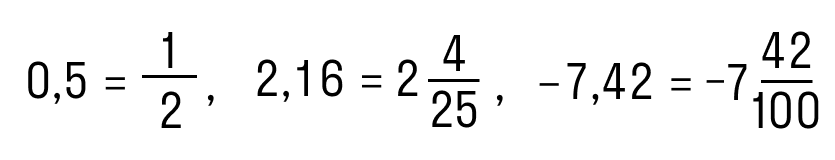
Обыкновенная дробь может быть преобразована в конечную десятичную дробь только в том случае, если знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:

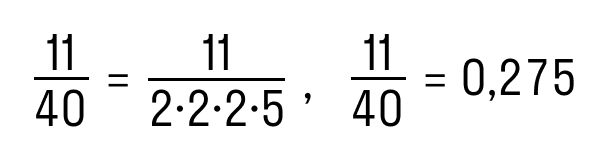
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель делится на 2 и 5.

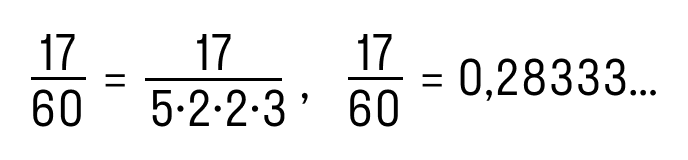
Дробь 17/60 нельзя перевести в конечную десятичную дробь, потому что в знаменателе, кроме множителей 2 и 5, стоит 3.

А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов преобразования обыкновенной дроби в десятичную.

Алгоритм преобразования

Акт преобразования десятичной дроби в простую относится к элементарным операциям. Есть несколько способов перевода. Какой из них выполнить, зависит от личных предпочтений лица, принимающего решение. Например, выражение 3.2 также можно записать как 16/5.

Другими словами, математики договорились, что, когда речь идет о простых числах, нули опускаются, а вместо них ставится запятая, отделяющая целую часть. Это было сделано для облегчения восприятия записи и для удобства подсчета.

Правило для наиболее часто используемого метода перевода заключается в следующем. Если в знаменателе стоит число, кратное десяти, нужно просто переписать числитель, затем подсчитать количество цифр, совпадающих с числом в знаменателе, и поставить после них запятую. Подсчет количества разделенных цифр необходимо начинать с правой стороны. Также, если количество нулей превышает количество цифр в делителе, то пропущенное их количество пишется перед числом.

Выполняемые операции, кроме получения периодической дроби, можно производить и в обратном направлении. Остаток от деления всегда должен быть меньше делителя. Поэтому, если в результате действия получается нуль, деление останавливается, а если в остатке — бесконечное периодическое отношение.

Чаще всего для преобразования простой дроби в десятичную нужно выполнить три шага:

1. Сократите выражение, которое необходимо преобразовать.
2. Разделите числитель на знаменатель практичным способом. В зависимости от размера значений в числителе и знаменателе это можно сделать в столбце или в баках. Если при делении получается ненулевой остаток, поставьте запятую и продолжайте искать частное.
3. Запишите найденный результат через запятую.

Способ 1. Превращаем знаменатель в 10, 100 или 1000

Чтобы преобразовать дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число так, чтобы знаменатель стал равен 10, 100, 1000 и т д. Но прежде чем продолжить расчеты, необходимо проверить, можно ли преобразовать это дробь вообще в десятичную.

Возьмем, к примеру, дробь 3/20. Его можно сократить до последнего десятичного знака, потому что знаменатель делится на 2 и 5.

Мы можем получить 100 внизу: просто умножьте 20 на 5. Не забывайте и о верхней части: мы получаем 15.

Теперь напишем счетчик отдельно. Отсчитываем справа столько знаков, сколько нулей в знаменателе, и ставим запятую. В нашем примере знаменатель равен 100 (в нем два нуля), поэтому после подсчета двух цифр ставим запятую и получаем 0,15. Трансформация готова.

Другой пример:

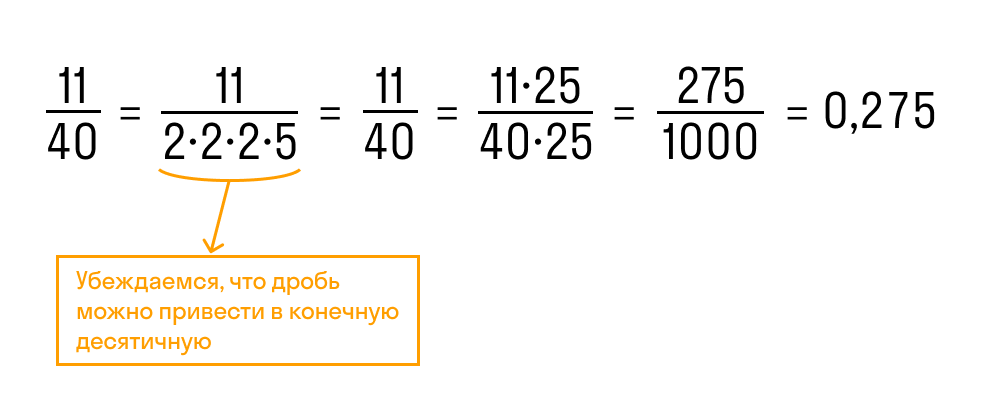
Способ 2. Делим числитель на знаменатель

Чтобы преобразовать обыкновенную дробь в десятичную, достаточно разделить верхнюю часть на меньшую. Проще всего это сделать, конечно, с помощью калькулятора — но его не разрешают использовать в тестах, поэтому мы учимся по-другому.

Возьмем, к примеру, дробь 78/100. Давайте удостоверимся, что дробь можно сократить до последнего десятичного знака.

Делим числитель на знаменатель столбиком — преобразование готово:

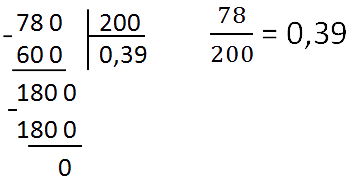
Если при делении на угол выяснилось, что процесс не заканчивается и повторяющиеся числа выстраиваются в ряд после запятой, то эту дробь нельзя преобразовать в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно в скобках записать повторяющееся число, вот так: 1/3 = 0,3333.. = 0, (3).

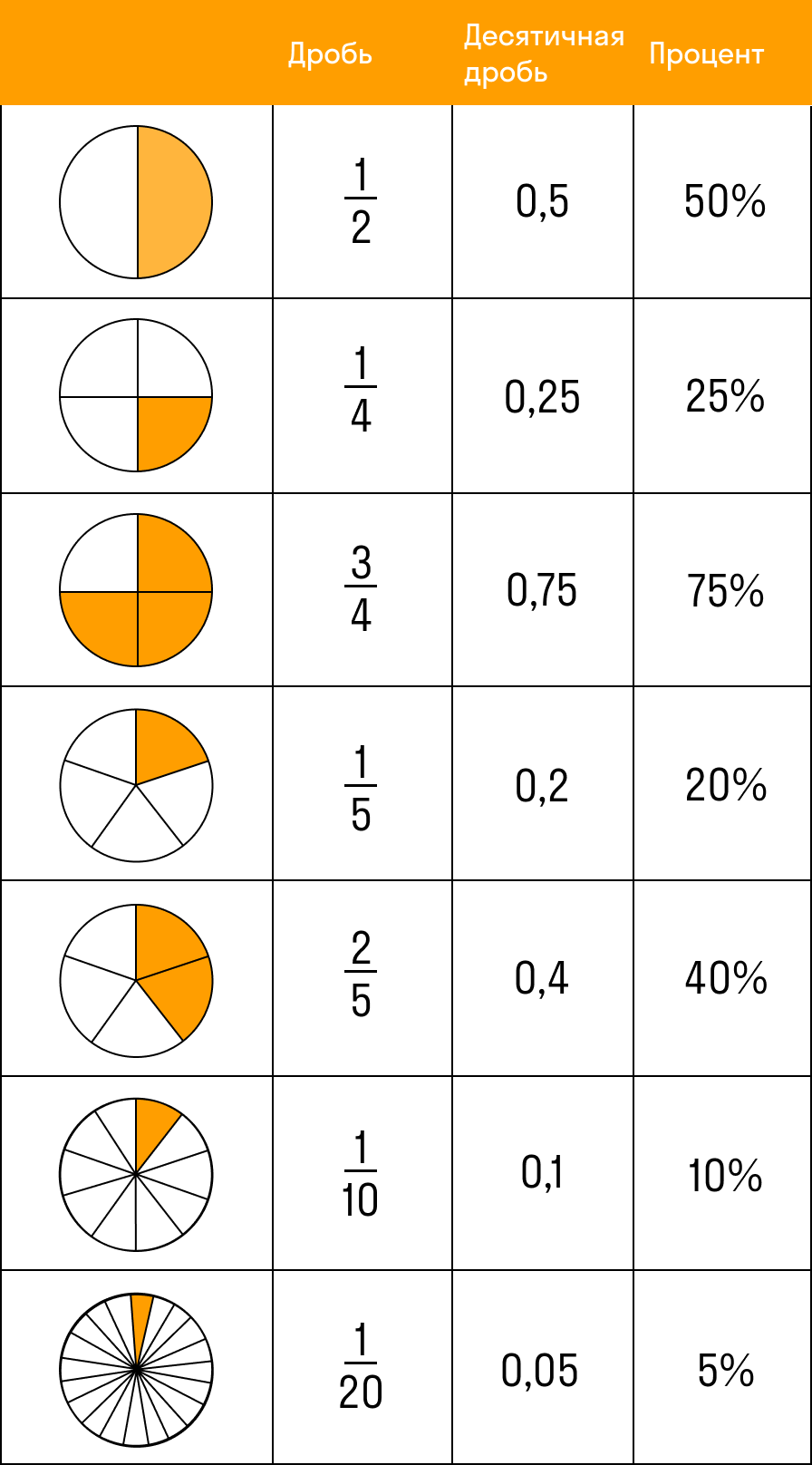
Для простоты мы составили таблицу дробей со знаменателями, которые чаще всего встречаются в математических задачах. Загрузите его на свой гаджет или распечатайте и сохраните в учебнике как закладку:

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.

Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.

Пример 4. Переведем число 159 из десятичной СС в двоичную СС:

159	2
158	79	2
1	78	39	2
	1	38	19	2
		1	18	9	2
			1	8	4	2
				1	4	2	2
					2	1

Рис. 1

Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:

Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.

615	8
608	76	8
7	72	9	8
	4	8	1
		1

Рис. 2

При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:

Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.

19673	16
19664	1229	16
9	1216	76	16
	13	64	4
		12

Рис. 3

Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.

Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.

Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).

Рассмотрим вышеизложенное на примерах.

Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.

		0.214
	x	2
	0.428
	x	2
	0.856
	x	2
1		0.712
	x	2
1		0.424
	x	2
	0.848
	x	2
1		0.696
	x	2
1		0.392

Рис. 4

Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.

Следовательно можно записать:

Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.

		0.125
	x	2
	0.25
	x	2
	0.5
	x	2
1		0.0

Рис. 5

Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:

Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.

		0.214
	x	16
3		0.424
	x	16
6		0.784
	x	16
12		0.544
	x	16
8		0.704
	x	16
11		0.264
	x	16
4		0.224

Рис. 6

Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:

Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.

		0.512
	x	8
4		0.096
	x	8
	0.768
	x	8
6		0.144
	x	8
1		0.152
	x	8
1		0.216
	x	8
1		0.728

Рис. 7

Получили:

Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:

Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:

Вариант 3: Дробь с горизонтальным разделителем

Добавить в текстовый документ Ворд дробь с горизонтальным разделителем между числителем и знаменателем можно одним из двух методов – используя средства вставки уравнений или специальный код с его последующим преобразованием.

Способ 1: Вставка формулы

В Microsoft Word имеется набор инструментов для работы с математическими выражениями, для чего можно как использовать уже готовые формулы и уравнения (например, бином Ньютона или площадь круга), так и «собирать» их самостоятельно из более простых записей. В числе последних есть и интересующая нас в рамках настоящей статьи дробь с горизонтальным разделителем.

1. Откройте вкладку “Вставка” и выберите в группе “Символы” пункт “Уравнение”.

1. Нажав на кнопку “Уравнение”, выберите пункт “Вставить новое уравнение”.

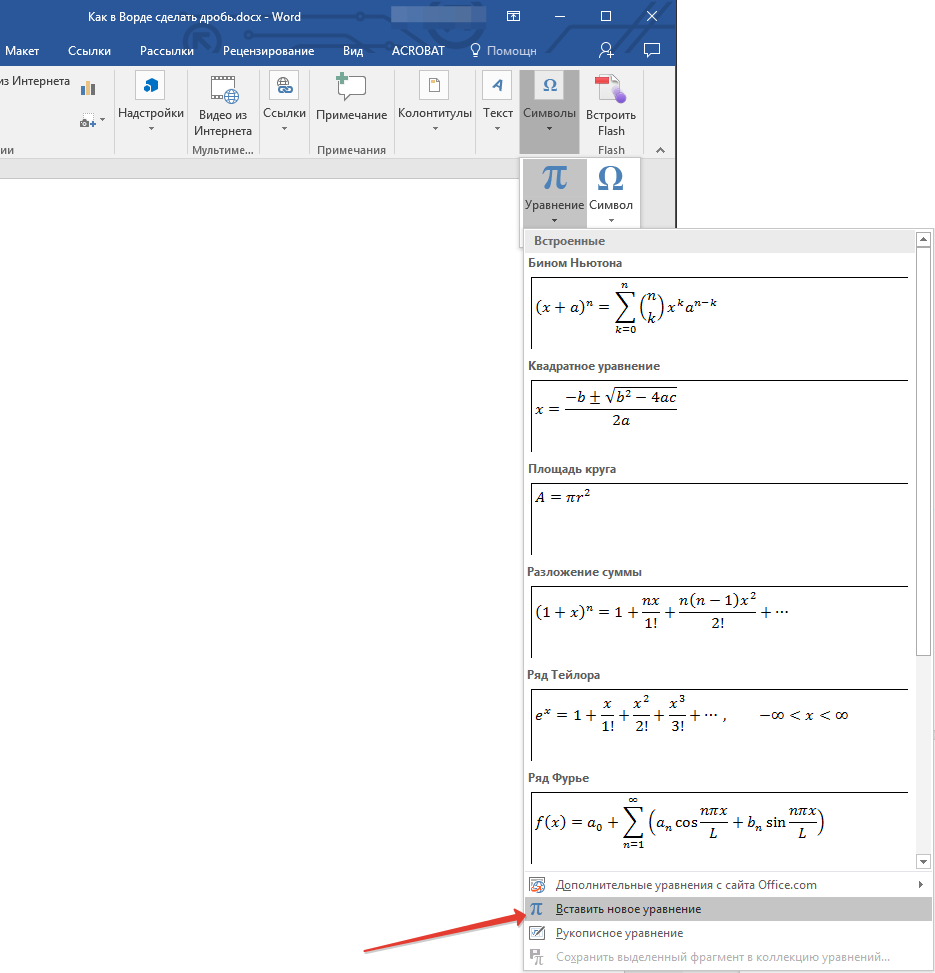
1. Во вкладке “Конструктор”, которая появится на панели управления, нажмите на кнопку “Дробь”.

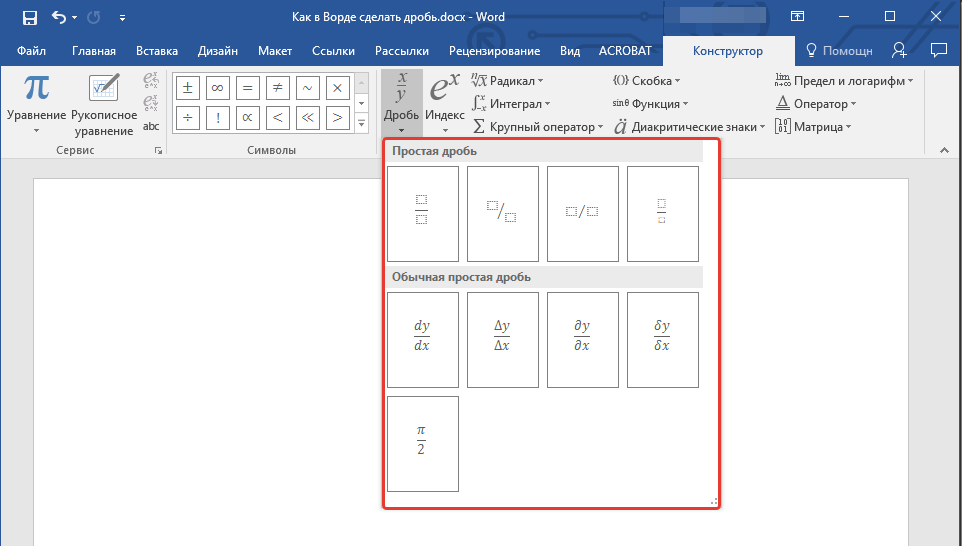
1. В развернувшемся меню выберите в разделе “Простая дробь” тип дроби, которую Вы хотите добавить — через слеш или горизонтальную линию.

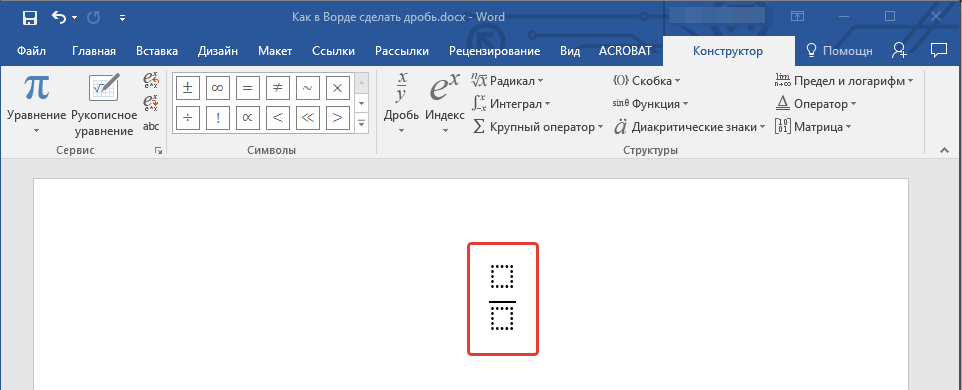
1. Макет уравнения изменит свой внешний вид, впишите в пустые графы необходимые числовые значения.
2. Кликните по пустой области на листе, чтобы выйти из режима работы с уравнением/формулой.

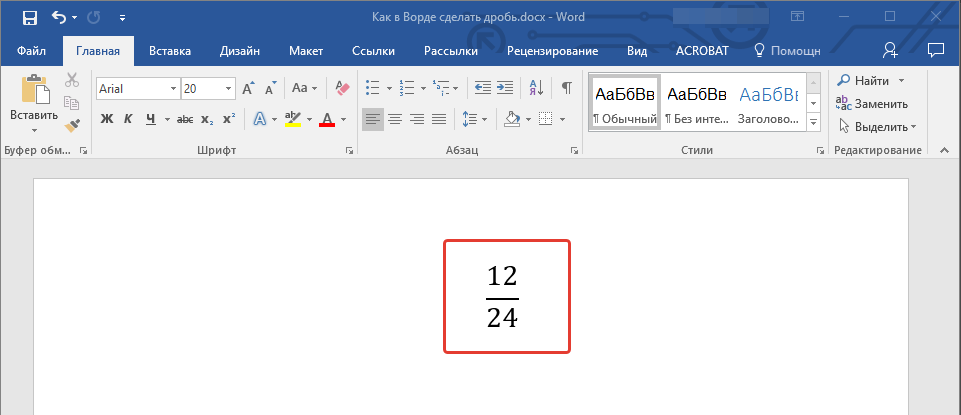
Именно написание дроби через меню вставки нового уравнения является оптимальным решением нашей сегодняшней задачи, тем более, что таким образом можно добавлять выражения обоих типов — и те, что разделены слешем (косой чертой), и те, которые разделяются горизонтальной полосой. Особенно актуально использование этого метода в случае, когда одними дробями работа не ограничивается и требуется писать и другие математические выражения.

Способ 2: Коды полей с ключами

Более простой в своей реализации альтернативой предыдущему решению является написание дробей с горизонтальным разделителем путем ввода и преобразования специального кода поля с ключом. Делается это следующим образом:

1. Установите указатель курсора в том месте текстового документа, где будет записана дробь.

Нажмите на клавиши «Ctrl+F9» (обратите внимание, что на ряде ноутбуков, где F-клавиши по умолчанию выполняют мультимедийные функции, дополнительно может потребоваться нажать клавишу «Fn», то есть сочетание в таком случае будет «Ctrl+Fn+F9»)

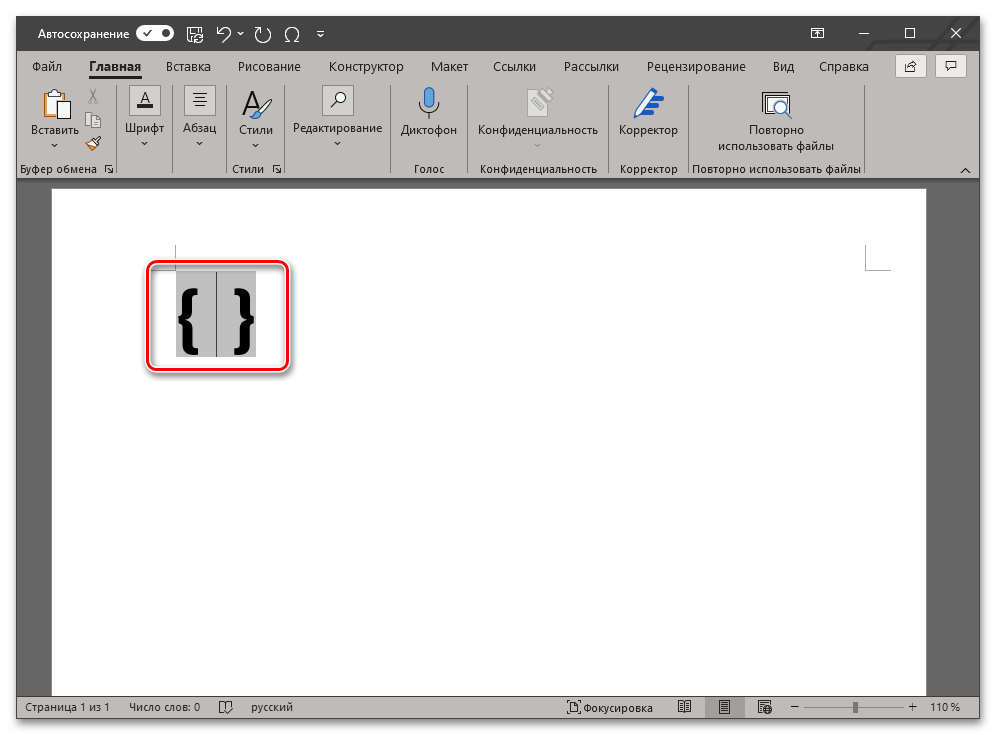
В выбранном месте документа появятся фигурные скобки с мигающей между ними кареткой (указатель курсора). Не перемещаясь из этой области, введите код следующего вида:

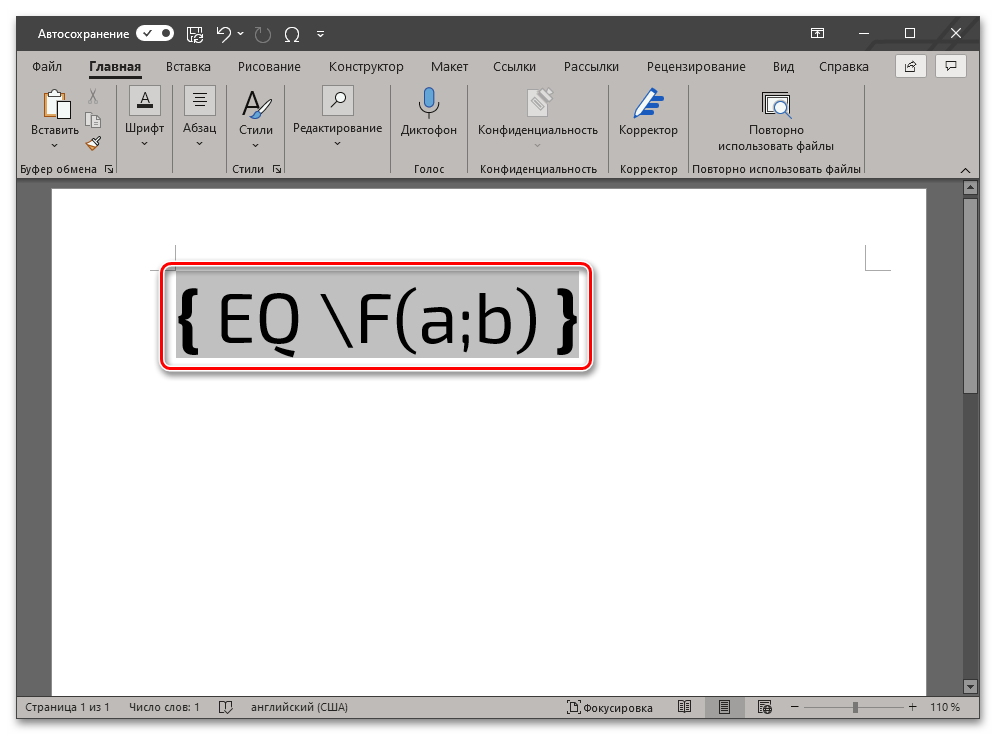
• EQ создает поле для ввода формулы;
• F создает дробь с горизонтальным разделителем и выравнивает относительно этой линии числитель и знаменатель;
• a и b – числитель и знаменатель, то есть вместо этих букв нужно вводить соответствующие им значения. Например, чтобы записать таким образом 2/3, следует использовать указанный ниже код:

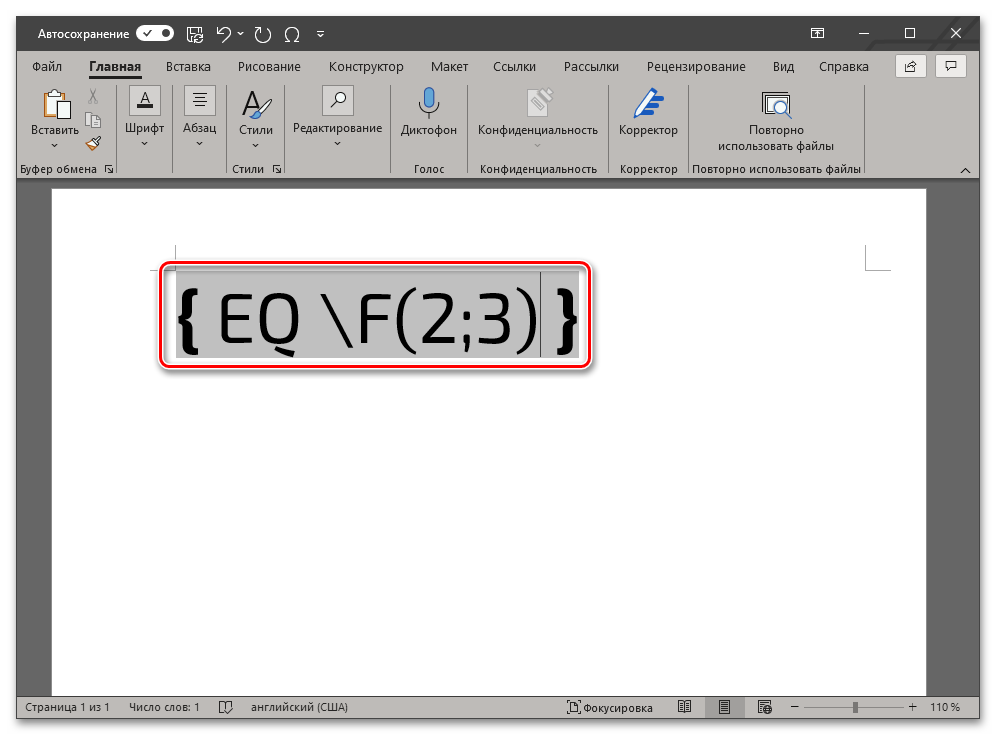
1. Разобравшись со всеми параметрами кода и указав его в том виде, который соответствует желаемой дроби, не перемещая указатель курсора и не покидая обозначенное фигурными скобками поле для ввода, нажмите на клавишу «F9» (опять же, на ноутбуках может потребоваться нажать «Fn+F9»).

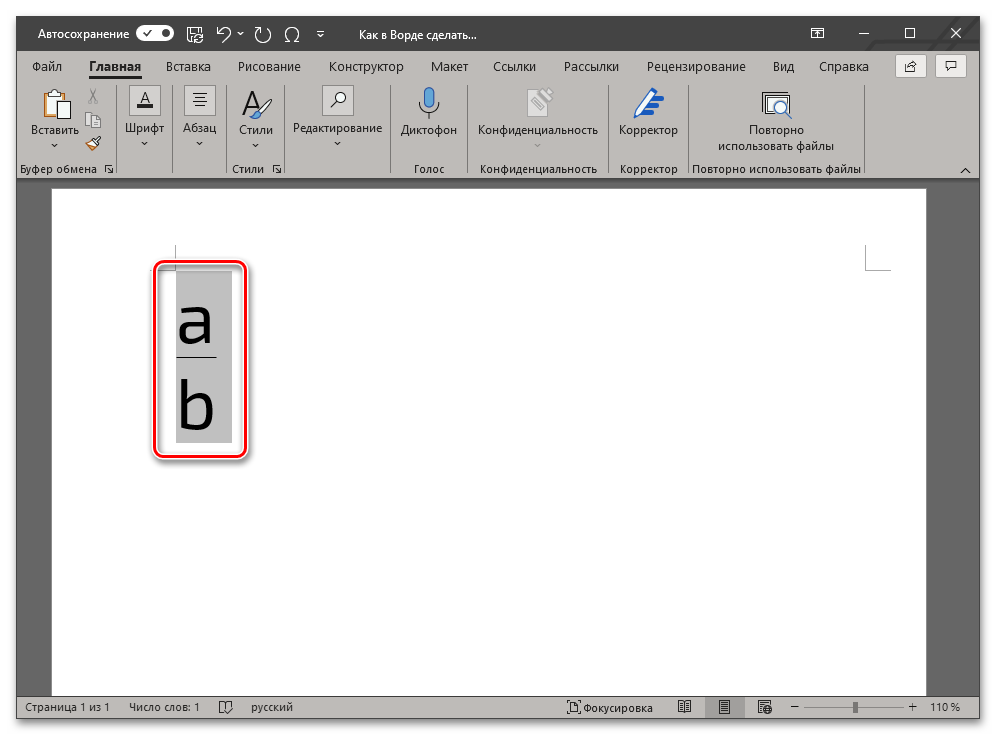
1. В результате выполнения предыдущего шага инструкции код будет преобразован в дробь с горизонтальным разделителем между числителем и знаменателем, что показано на представленных выше и ниже изображениях.

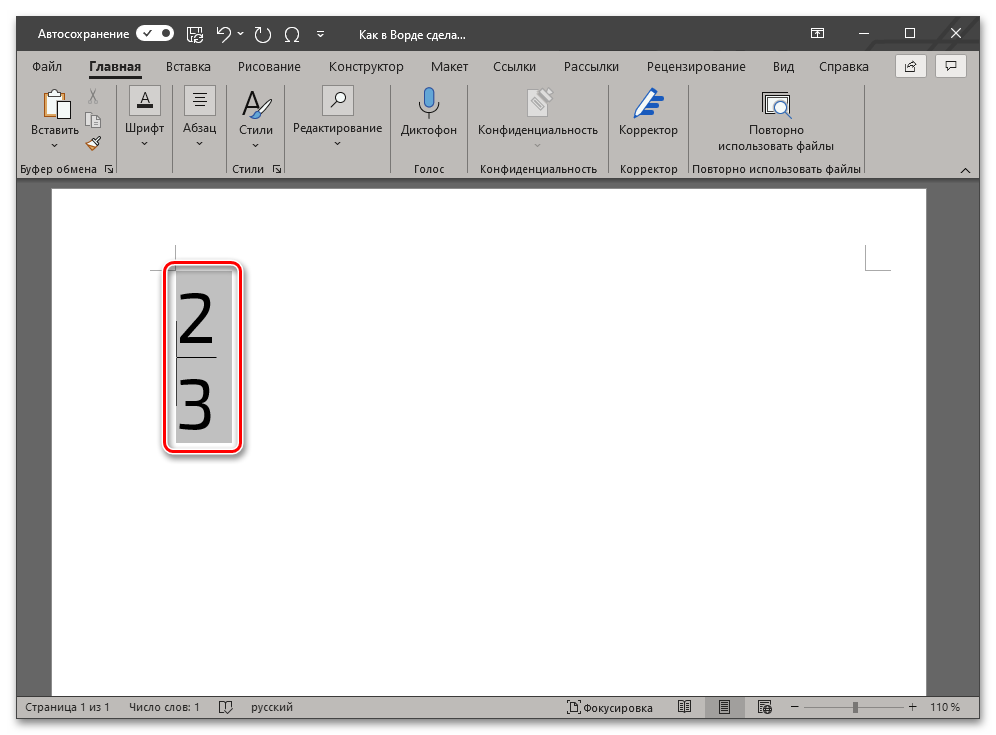
Этот метод является не только более простым и удобным в своем реализации, чем предыдущий, но и лишен характерных для него ограничений. Так, у записанной дроби отсутствует видимое поле (рамка), она выглядит более эстетично и является пригодной для общего форматирования, представляется в виде используемого по умолчанию для ввода текста шрифте, который по необходимости можно изменить на любой другой.

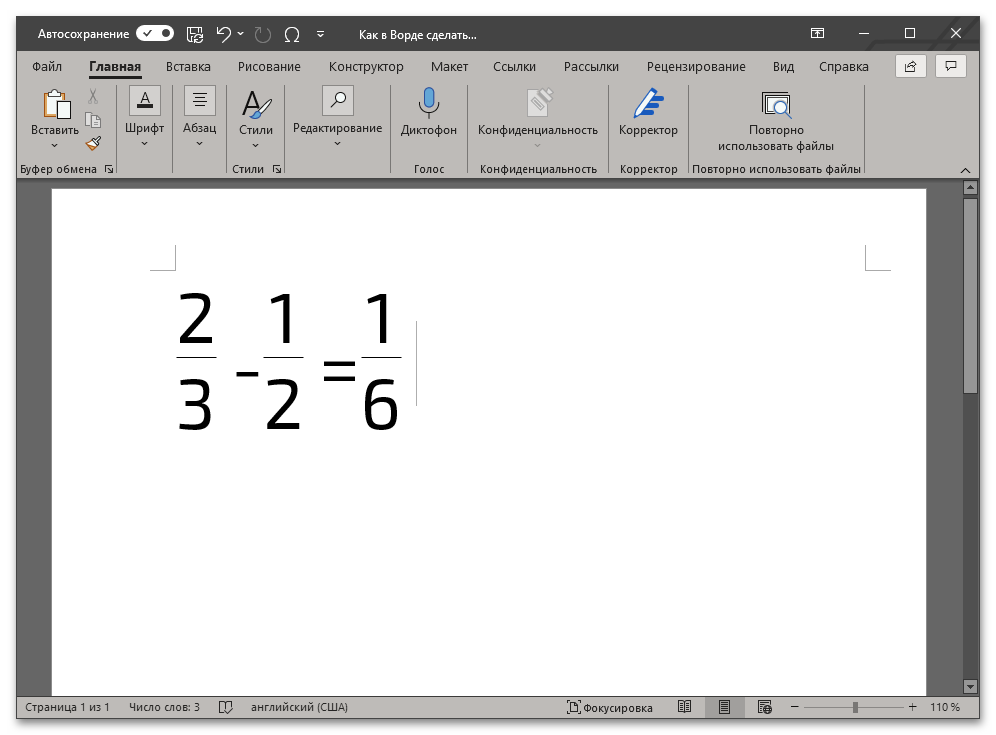
Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?

Правило перевода десятичных дробей в обыкновенные дроби

1. В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
2. В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
3. При необходимости сокращаем полученную обыкновенную дробь. 

Рассмотрим применение данного правила на примерах.

Пример 8. Перевод десятичных дробей в обыкновенные

Представим число 3,025 в виде обыкновенной дроби.

1. В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
2. В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 30251000.
3. Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.

Пример 9. Перевод десятичных дробей в обыкновенные

Переведем дробь ,0017 из десятичных в обыкновенные.

1. В числителе запишем дробь ,0017, отбросив запятую и нули слева. Получится 17.
2. В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?

Сформулируем еще одно правило.

Правило перевода десятичных дробей в смешанные числа.

1. Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
2. В числителе  записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
3. В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Обратимся к примеру

Пример 10. Перевод десятичной дроби в смешанное число

Представим дробь 155,06005 в виде смешанного числа.

1. Записываем число 155, как целую часть.
2. В числителе записываем цифры после запятой, отбросив нуль. 
3. В знаменателе записываем единицу и пять нулей

Поучаем смешанное число: 1556005100000

Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:

155,06005=155120120000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.

Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример 11. Перевод периодической десятичной дроби в обыкновенную

Обратим периодическую дробь 3,75().

Отбросив нули справа, получим конечную десятичную дробь 3,75.

Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:

3,75()=3,75=375100=154.

Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:

,(74)=,74+,0074+,000074+,00000074+..

Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что <q<1, то сумма равна b1-q.

Рассмотрим несколько примеров с применением данной формулы.

Пример 12. Перевод периодической десятичной дроби в обыкновенную

Пусть у нас есть периодическая дробь ,(8) и нам нужно перевести ее в обыкновенную.

Запишем:

,(8)=,8+,08+,008+..

Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом ,8 и знаменателем ,1.

Применим формулу:

,(8)=,8+,08+,008+..=,81-,1=,8,9=89

Это и есть искомая обыкновенная дробь.

Для закрепления материала рассмотрим еще один пример.

Пример 13. Перевод периодической десятичной дроби в обыкновенную

Обратим дробь ,43(18).

Сначала записываем дробь в виде бесконечной суммы:

,43(18)=,43+(,0018+,000018+,00000018..)

Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:

,0018+,000018+,00000018..=,00181-,01=,0018,99=189900.

Полученное прибавляем к конечной дроби ,43=43100 и получаем результат:

,43(18)=43100+189900

После сложения данных дробей и сокращения получим окончательный ответ:

,43(18)=1944

В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Перевод десятичных дробей в обыкновенные дроби

Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.

Перевод конечных десятичных дробей в обыкновенные дроби

Рассмотрим решения примеров.

Обратите десятичную дробь 3,025 в обыкновенную дробь.

В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.

Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь.

В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4 цифры.

Рассмотрим пример перевода десятичной дроби в смешанное число.

Представьте десятичную дробь 152,06005 в виде смешанного числа

Число 152 до десятичной запятой есть целая часть искомого смешанного числа.

На этом перевод конечной десятичной дроби 152,06005 в смешанное число закончен.

Перевод периодических дробей в обыкновенные дроби

Любую периодическую десятичную дробь можно перевести в обыкновенную дробь. На примерах разберем способ, позволяющий осуществить такой переход.

Начнем с самых простых случаев, когда период дроби есть 0. Периодические дроби с периодом 0 можно заменить равными им конечными десятичными дробями, для этого достаточно отбросить все нули справа. Таким образом, перевод в обыкновенные дроби периодических дробей с периодом 0 сводится к обращению конечных десятичных дробей.

Запишите периодическую дробь 3,75(0) в виде обыкновенной дроби.

Напомним, что сумма членов бесконечно убывающей геометрической прогрессии с первым членом b и знаменателем q ( 0 ) равна .

Теперь можно рассмотреть решения нескольких примеров.

Переведите периодическую дробь 0,(8) в обыкновенную дробь.

Для закрепления материала разберем решение еще одного примера.

Представьте бесконечную десятичную периодическую дробь 0,43(18) в обыкновенную дробь.

Бесконечные непериодические десятичные дроби не переводятся в обыкновенные дроби

Выше мы выяснили, что любая обыкновенная дробь переводится либо в конечную десятичную дробь, либо в периодическую десятичную дробь. Отсюда следует, что никакая бесконечная непериодическая десятичная дробь не может быть переведена в обыкновенную дробь, так как полученную обыкновенную дробь нельзя будет перевести обратно в эту бесконечную непериодическую дробь.

Арифметические действия с обыкновенными дробями

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.

При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем  сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

 Умножение дробей

1. Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
2. При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

 Деление дробей

Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.