Калькулятор процентов (простых)

Как посчитать, на сколько процентов одно число меньше другого

Самый быстрый и удобный способ узнать разницу между числами в процентах — использовать калькулятор расчета процентов в онлайн режиме. Однако все вычисления можно легко выполнить вручную.

Для нахождения данного значения используется аналогичная формула, что и при расчёте, насколько одно число больше другого:

1. Разделить одно число на другое. Так находится отношение первого значения ко второму.

2. Полученное отношение умножить на 100.

3. Результат первых двух вычислений вычесть из 100. Полученное значение покажет, насколько одно число меньше другого.

Пример: узнать, насколько процентов 10 меньше 20.

• 100-(10:20×100)=50%;

• 10:20=0,5;

• 0,5×100=50;

• 100-50=50%. Итогом последнего действия станет вычисляемый процент.

Ответ: 10 меньше 20 на 50%.

Полезные советы

Вот несколько советов, которые могут помочь при расчете процентов:

1. Освойте основные формулы для расчета процентов, такие как формулы для нахождения процентного соотношения, процентного приращения или процентного уменьшения.
2. Помните, что проценты могут быть выражены как десятичные дроби, например, 50% может быть записано как 0.5.
3. Не забывайте учитывать порядок операций, например, в выражении «25% от 80» сначала нужно умножить 80 на 0,25, а затем округлить результат.
4. Используйте дроби для более точных расчетов, особенно если нужно произвести несколько операций. Например, вы можете записать «25% от 80» как 1/4 от 80.
5. Учитывайте различные типы процентов, например, простые и сложные проценты. Для расчета сложных процентов вам может потребоваться использовать формулу с учетом периода начисления процентов.
6. Используйте калькулятор при необходимости, особенно при более сложных расчетах. Это может помочь избежать ошибок при пересчете значений.
7. Не забывайте проверять свои расчеты на ошибки и перепроверять полученные результаты, чтобы убедиться в их правильности.

Вопросы и ответы

Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.

Как вычислить процент от числа?

Для вычисления процента от числа нужно умножить число на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти 25% от числа 200, нужно выполнить следующее вычисление: 200 x 0,25 = 50.

Как вычислить число, которому соответствует определенный процент?

Чтобы найти число, соответствующее определенному проценту, нужно разделить процентное значение на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти число, которому соответствует 20%, нужно выполнить следующее вычисление: 20 ÷ 100 x N = N x 0,2.

Как вычислить процент изменения?

Чтобы вычислить процент изменения, нужно найти разницу между начальным и конечным значениями, разделить ее на начальное значение и умножить на 100%. Например, если начальное значение равно 100, а конечное значение равно 120, то процент изменения будет: ((120-100) ÷ 100) x 100% = 20%.

Как вычислить начальное значение при известном конечном значении и процентном изменении?

Чтобы найти начальное значение при известном конечном значении и процентном изменении, нужно разделить конечное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если конечное значение равно 120, а процент изменения равен 20%, то начальное значение будет: 120 ÷ (1 + 0,2) = 100.

Как вычислить конечное значение при известном начальном значении и процентном изменении?

Чтобы найти конечное значение при известном начальном значении и процентном изменении, нужно умножить начальное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если начальное значение равно 100, а процент изменения равен 20%, то конечное значение будет: 100 x (1 + 0,2) = 120.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Сколько часов в месяце. Введите количество месяцев, чтобы узнать, сколько в них часов.
• Сколько часов в неделе. Введите количество недель, чтобы узнать, сколько в них часов.
• Калькулятор дней между датами. Определите точное количество дней между любыми двумя датами для планирования или информационных целей.
• Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
• Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
• Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
• На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
• На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
• Инженерный калькулятор. Посчитайте сложные примеры на продвинутом калькуляторе.
• Калькулятор сложного процента. Рассчитайте на инвесткалькуляторе сумму, полученную в результате применения сложного процента с реинвестированием, регулярным пополнением, капитализацией и с примерами.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Как высчитать процентное соотношение

Процентное соотношение определяет, какой процент от первого числа составляет второе значение, или наоборот. Для проведения расчета необходимо взять оба показателя и применить формулу:

R%= N1:N2×100%

Расшифровка:

1. R% — процентое соотношение чисел. Именно его необходимо найти в данном случае.

2. N1 и N2 — числа, для которых находится соотношение. Для удобства и правильности рассчетов N1 должно быть меньше N2.

3. Знак : означает, что числа нужно разделить. N1 делится на N2.

4. ×100% — последнее действие. После нахождения частного от N1 и N2 следует умножить его на 100%. Получившееся значение будет равно процентному соотношению чисел.

Пример: найти процентое соотношение 20 к 40.

• R%=20:40×100%;

• 20:40=0,5;

• 100%×0,5=50%.

Ответ: соотношение 20 к 40 составляет 50%.

Примеры школьных заданий

Из запланированной дистанции в 32 км Том пробежал только 76%. Сколько километров пробежал мальчик?
Решение: для вычислений подходит первый калькулятор. В первую ячейку вставляем 76, во вторую — 32.
Получаем: Том пробежал 24.32 км.

Фермер Купер собрал с поля 500 кг кукурузы. 160 кг из этой массы оказалось неспелой. Сколько процентов от общего числа составила неспелая кукуруза?
Решение: для расчёта подходит второй калькулятор. В первое окошко записываем число 160, во второе — 500.
Получаем: 32% кукурузы оказалось неспелой.

Майкл прочитал своей подруге на ночь 112 страниц, что составляет 32% всей книги. Сколько страниц в книге?
Решение: используем для расчёта третий калькулятор. Вставляем в первую ячейку значение 112, а во вторую — 32.
Получаем: в книге 350 страниц.

Длина маршрута, по которому ходил автобус №42, составляла 48 километров. После добавления трёх дополнительных остановок расстояние от начальной до конечной станции изменилось до 78 километров. На сколько процентов изменилась длина маршрута?
Решение: используем для вычисления четвёртый калькулятор. В первую ячейку вбиваем число 78, во вторую — 48.
Получаем: длина маршрута выросла на 62.5%.

Братство металла и макулатуры в мае сдало на лом 320 кг цветного металла, а в июне на 30% больше. Сколько металла сдали ребята из братства в июне?
Решение: для расчёта будем использовать пятый калькулятор. В первую ячейку вставляем число 30, а во второе число 320.
Получаем: в июне братство сдало 416 кг металла.

Энди прорыл во вторник 3 метра туннеля, а в среду в связи с отъездом друга в Ирландию — на 22% меньше. Сколько метров туннеля прорыл Энди в среду?
Решение: в данном случае подходит шестой калькулятор. В первую ячейку вставляем 22, во вторую — 3.
Получаем: в среду мальчик прорыл 2.34 метра туннеля.

Как вычислить процент от процента

Первым действием превращаем проценты в части. Чтобы получить части, каждое число со знаком процента делим на 100, в результате получаем десятичные дроби. После чего десятичные дроби умножаем на друг друга. Полученную десятичную дробь умножаем на число без знака процента.

Первый пример

Найдем 45 % от 76.

Вычислим 25 % от 45 %.

Первым действием 45 и 25 делим на 100, получаем 0,45; 0,25. Умножаем полученные десятичные дроби друг на друга в ответе получаем 0,1125. Далее 0,1125 умножаем на 76 и в конечном ответе получаем 8,55.

Записывались следующие выражения для решения задачи:

1. 45:100 = 0,45;
2. 25:100 = 0,25;
3. 0,45 * 0,25 = 0,1125;
4. 76 * 0,1125 = 8,55.

Второй пример

Найдем 67 % от 87

Найдем 58 % от 67 %.

Решение задачи будет выглядеть в виде следующих выражений:

1. 67:100 = 0,67;
2. 58:100 = ,58;
3. 0,58 * ,67 = 0,3886;
4. 87 * 0,3886 = 33,8082.

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь    означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

6. Формула расчета простых процентов. Расчет процентов на банковский вклад

Если проценты на депозит начисляются один раз в конце срока вклада, то расчет процентов выполняется по формуле простых процентов:

Sp = K * P/100 * d/D

Формула расчета вклада с процентами:

S = K + K * P/100 * d/D

Иногда удобнее использовать формулу расчета в таком виде:

S = K * (1 + P/100 * d/D)

Где:
S — сумма банковского вклада с процентами,
Sp — сумма процентов (доход),
K — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — количество дней начисления процентов по привлеченному вкладу,
D — количество дней в календарном году (365 или 366).

Пример 6.1 Банком принят вклад 100 тыс. рублей сроком на 1 год по ставке 20%.

S = 100000 + 100000 * 20/100 * 365/365 = 120000
Sp = 100000 * 20/100 * 365/365 = 20000

Пример 6.2 Банком принят вклад 100 тыс. рублей сроком на 30 дней по ставке 20% годовых.

S = 100000 + 100000 * 20/100 * 30/365 = 101643.84
Sp = 100000 * 20/100 * 30/365 = 1643.84

Онлайн калькулятор
Расчет вклада с процентами

8. Формула сложных процентов если процентная ставка дана не в годовом исчислении

Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула расчета сложных процентов выглядит так:

S = K * ( 1 + P/100 )N

Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — процентная ставка,
N — количество периодов начисления процентов.

Формула расчета процентов на вклад:

Sp = S — K

или

Sp = K * ( 1 + P/100 )N — K

Иногда удобнее использовать формулу расчета в таком виде:

Sp = K * (( 1 + P/100 )N — 1)

Пример 8.1 Принят депозит 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5% в месяц.

S = 100000 * (1 + 1.5/100)3 = 104 567.84
Sp = 100000 * ((1 + 1.5/100)3 — 1) = 4 567.84

Онлайн калькулятор
Расчет вклада с процентами

По теме страницы

Список таблиц финансовых расчетовФормулы расчета процентов по вкладуФормулы расчета сложных процентов и выбор вкладаФормулы расчета НДС, сумма с НДС, сумма без НДС, выделение НДСФормула расчета кредита. Аннуитет, аннуитетные платежи, коэфициент аннуитета, формула аннуитетных платежейФормула финансового рычага (финансового левериджа)ДисконтированиеКарта сайта — Подробное оглавление сайта

7. Формула расчета сложных процентов. Расчет процентов на банковский вклад при начислении процента на процент

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то расчет вклада с процентами выполняется по формуле сложных процентов.

S = K * ( 1 + P/100 * d/D )N

Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — продолжительность периода в конце которого начисляются проценты,
N — количество периодов начисления процентов.

При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход), вычтя сумму начального вклада (капитал).

Формула расчета процентов:

Sp = S — K

или

Sp = K * ( 1 + P/100 * d/D )N — K

Иногда удобнее использовать формулу расчета в таком виде:

Sp = K * (( 1 + P/100 * d/D )N — 1)

Пример 7.1 Принят вклад 100 тыс. рублей сроком на 90 дней по ставке 20% годовых с начислением процентов каждые 30 дней.

S = 100000 * (1 + 20/100 * 30/365)3 = 105 013.02
Sp = 100000 * ((1 + 20/100 * 30/365)3 — 1) = 5 013.02

Онлайн калькулятор
Расчет вклада с процентами

Расчет процентов

Sp =

Пример 7.2 Проверим формулу расчета сложных процентов для случая из предыдущего примера.

Разобьем срок вклада на 3 периода и сделаем расчет процентов для каждого периода, использую формулу простых процентов.

S₁ = 100000 + 100000*20/100 * 30/365 = 101643.84
Sp₁ = 100000 * 20/100 * 30/365 = 1643.84
S₂ = 101643.84 + 101643.84*20/100 * 30/365 = 103314.70
Sp₂ = 101643.84 * 20/100 * 30/365 = 1670.86
S₃ = 103314.70 + 103314.70*20/100 * 30/365 = 105013.02
Sp₃ = 103314.70 * 20/100 * 30/365 = 1698.32

Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)

Sp = Sp₁ + Sp₂ + Sp₃ = 5013.02

Таким образом, формула расчета сложных процентов верна.

Где можно применить калькулятор процентов

Если требуется проводить вычисления, связанные с процентами, то полезным инструментом будет калькулятор операций с процентами. Его применение возможно в множестве областей, таких как:

• Финансы, для расчета процентов по кредитам, вкладам, ипотеке, инвестициям, налогам, облигациям и другим операциям;
• Бизнес, для налоговых расчетов, расчета общей суммы платежей за товары и услуги, налоговых вычетов, маржинальности и других операций;
• Образование, для расчета оценок, процентов скидок на учебники, успешных сдач экзаменов и других задач;
• Личные финансы, для расчета бюджета, расходов на различные категории, процентов от заработной платы, калькуляторов кредитных карт и прочего;
• Медицина, для расчета процентов смертности, выживаемости, процентов телесной жировой массы и прочих данных;
• Также калькулятор процентов может быть полезен для обучения математике и использования в повседневной жизни для быстрых расчетов.

Как найти сколько процентов составляет одно число от другого числа

Мы поговорим о нахождении процентного отношения двух чисел. Тема достаточно распространенная в математике, потому что нам очень часто придется вычислять проценты. И самое главное, что процентное отношение двух чисел очень часто применяется во всех сферах деятельности. В жизненных задачах, но ничего здесь сложного нет, нечего бояться.

Процентное отношение указывает, какой процент число составляет от второго числа. Чтобы найти процентное отношение – стоит найти отношение чисел, узнать отношение можно просто разделив их на друг друга, сложности в этом нет. А чтобы найти процентное соотношение – нужно ответ, получившийся в результате нахождения отношения чисел, умножить на сотню.

Решим несколько примеров нахождения процента одного числа от другого.

Первый пример

Найдем процентное отношение 18:6. Чему равно это отношение? Записываем числа 18 и 6 в дробь и получаем запись 18/6. 18 делим на 6, в ответе будет 3. Переходим к процентному отношению. Для нахождения процентного отношения требуется 3 умножить на 100 и это будет 300 %. Все довольно просто.

По ходу решения задачи получились следующие записи:

1. 18:6 = 18/6 = 3;
2. 3 * 100% = 300 %.

Второй пример

В качестве 2 примера найдем процентное соотношение 48 и 24. Как и в первом примере записываем числа дробью, получаем 48/24. 48/24 = 2. Мы нашли отношение чисел 48 и 24. Теперь находим процентное отношение – 2 умножаем на 100.

Ответ: 200 %

По ходу решения задачи, мы получили следующие выражения:

1. 48:24 = 48/24 = 2;
2. 2 * 100 = 200.

Формулы расчёта процентов

1. Какое число соответствует 24% от числа 286?
   Определяем 1% от числа 286: 286 / 100 = 2.86.
   Рассчитываем 24%: 24 · 2.86 = 68.64.
   Ответ: 68.64%.
   Формула вычисления x% от числа y: x · y / 100.
2. Сколько процентов составляет число 36 от 450?
   Определяем коэффициент зависимости: 36 / 450 = 0.08.
   Переводим результат в проценты: 0.08 · 100 = 8%.
   Ответ: 8%.
   Формула для определения, какой процент составляет число x от y: x · 100 / y.
3. От какой величины число 8 составляет 32%?
   Определяем 1% значения: 8 / 32 = 0.25.
   Вычисляем 100% величины: 0.25 · 100 = 25.
   Ответ: 25.
   Формула для определения числа, если x составляет его y %: x · 100 / y.
4. На сколько процентов число 128 больше 104?
   Определяем разницу значений: 128 — 104 = 24.
   Находим процент от числа: 24 / 104 = 0.23.
   Переводим результат в проценты: 0.23 · 100 = 23%.
   Ответ: 23%.
   Формула для определения насколько число x больше числа y: (x — y) · 100 / x.
5. Сколько будет, если прибавить 12% к числу 20?
   Определяем 1% от числа 20: 20 / 100 = 0.2.
   Рассчитываем 12%: 0.2 · 12 = 2,4.
   Добавляем полученное значение: 20 + 2.4 = 22.4.
   Ответ: 22.4.
   Формула для прибавления x% к числу y: x · y / 100 + y.
6. Сколько будет, если вычесть 44% из числа 78?
   Определяем 1% от числа 78: 78 / 100 = 0.78.
   Рассчитываем 44%: 0.78 · 44 = 34.32.
   Вычитаем полученное значение: 78 — 34.32 = 43.68.
   Ответ: 43.68.
   Формула для вычитания x% из числа y: y — x · y / 100.

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

Найти    от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби 

Получили 0,1. Теперь 0,1 умножаем на числитель дроби 

0,1 × 2 = 0,2

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

0,2 см = 2 мм

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

300 : 100 = 3

Теперь полученный результат умножаем на 50

3 × 50 = 150 руб.

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись  . Тогда задание будет выглядеть так: Найти  от 300 рублей, а решать такие задачи для нас пока проще

300 : 100 = 3

3 × 50 = 150

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

1200 : 100 = 12

12 × 32 = 384

Ответ: 384 костюмов нового фасона выпустила фабрика.

Как рассчитать разницу процентов двух чисел

В данной микротеме рассмотрим, как вычислять на сколько процентов число больше другого. При решении таких задачи 2 число разделится на первое, потом результат умножается на 100, а затем, чтобы получить конечный результат, из получившегося числа вычитаем сотню.

Первый пример

Вычислим на сколько процентов число 30 больше числа 7. Число 30 больше числа 7. Разделим 30 на 7, получим выражение 30/7. Данное отношение умножим на сотню, эта сотня идет как 100 процентов. Сто можно записаться как 100/1. Теперь мы видим, что на что нужно умножать, нужно 100 умножить на 30. В числителе после вычислений мы получим 3000, знаменатель 7. Теперь 3000/7 нам нужно вычесть из ста. Записывает 3000/7 с целой частью, получаем 428,4/7. И вычисляя из данного числа 100, получим 328,4/7

По ходу решения задачи получились следующие выражения:

1. 30/7 * 100/1 = 3000/7 = 428,4/7;
2. 428,4/7 – 100 = 328,4-7 %.

Второй пример

Разберем похожий пример, только в более короткой форме. Вычислим насколько процентов 70 больше 15. 70 делим на 15, получаем запись 70/15. Умножаем данную запись на 100/1, получаем 7000/15. Переводим 7000/15 в целые части, получаем 466,10/15. Вычитаем из 466,10/15 сотню, получаем конечный ответ 366,10/15. На столько процентов число 70 больше 15.

Получились следующие выражения:

1. 70/15 * 100/1 = 7000/15 = 466,10/15;
2. 466,10/15 – 100 = 366,10/15 %.

Как найти базовую сумму исходя из ее процента

В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?

Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:

67 / B * 100 = A

Подставляем значения:

67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)

Проверяем полученный результат с помощью формулы из первого способа:

293, 31 / 100 * 23 = 67

Всё сошлось.

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Как найти 100 %

Для нахождения 100 процентов, следует известную величину без знака процента умножить на 100 и разделить на количество известных процентов.

Первый пример

В классе 18 мальчиков – это 60 % всех учеников. Сколько учеников в классе.

В данной задаче стоит прибегнуть к пропорции. Запишем, что 18 учеников = 60 %. 100 % учащихся возьмем за Х, получается запись: Х учеников = 100%. Находим общее количество учеников. Запишем выражение:

Х уч. = 18 * 100/60 = 30.

Ответ: 30

Второй пример

В кл. 10 девочек – это 45 % от всех учеников. Сколько учеников в классе.

Для решения данной задачи, стоит записать данное выражение:

Х уч = 10 * 100/45 = 22.

Ответ: 22.

Значения других единиц, равные введённым выше

 открыть 

 свернуть 

Единицы количества

процент → единица (1)
процент → пара
процент → тройка
процент → полдюжины
процент → декада
процент → дюжина
процент → чертова дюжина
процент → скор (англ.)
процент → флок (англ.)
процент → шок (англ.)
процент → сотня
процент → большая сотня (англ.)
процент → гросс
процент → тысяча
процент → большой гросс

Единицы:

единица
(1)

 /
пара

 /
тройка

 /
полдюжины

 /
декада

 /
дюжина

 /
чертова дюжина

 /
скор (англ.)

 /
флок (англ.)

 /
шок (англ.)

 /
сотня

 /
большая сотня (англ.)

 /
гросс

 /
тысяча

 /
большой гросс

 открыть 

 свернуть 

Проценты и доли

процент → процент (%)
процент → промилле (‰)
процент → частей на миллион (ppm)
процент → частей на миллиард (ppb)

Единицы:

процент
(%)

 /
промилле
(‰)

 /
частей на миллион
(ppm)

 /
частей на миллиард
(ppb)

 открыть 

 свернуть 

Дроби

Внимание! Эта секция помогает ответить на вопросы такого типа: «Сколько 1/7-ых в одной половинке?» Чтобы получить ответ, введите 1 напротив 1/2 и посмотрите результат напротив 1/7. А теперь проверьте себя! Сможете при помощи нашего калькулятора быстро решить задачку: «Несколько одинаковых тортов разделили на 9 равных частей каждый, потом некоторые куски съели

Осталось 15 кусков. Если бы торты делили на 6 равных частей, и съели бы ровно такой же объём, сколько осталось бы кусков?». Наш калькулятор позволяет получить ответ в одно действие.

процент → половина (1/2)
процент → треть (1/3)
процент → четверть (1/4)
процент → одна пятая (1/5)
процент → одна шестая (1/6)
процент → одна седьмая (1/7)
процент → одна восьмая (1/8)
процент → одна девятая (1/9)
процент → одна десятая (1/10)
процент → одна шестнадцатая (1/16)
процент → одна тридцать вторая (1/32)

Единицы:

половина
(1/2)

 /
треть
(1/3)

 /
четверть
(1/4)

 /
одна пятая
(1/5)

 /
одна шестая
(1/6)

 /
одна седьмая
(1/7)

 /
одна восьмая
(1/8)

 /
одна девятая
(1/9)

 /
одна десятая
(1/10)

 /
одна шестнадцатая
(1/16)

 /
одна тридцать вторая
(1/32)

 открыть 

 свернуть 

Метрические префиксы

Эти префиксы широко используются в системе SI, могут применяться к любой единице. Например, килояблоко — это 1000 яблок.

процент → кекто (q)
процент → ронто (r)
процент → йокто (y)
процент → цепто (z)
процент → атто (a)
процент → фемто (f)
процент → пико (p)
процент → нано (n)
процент → микро (µ, mc)
процент → милли (m)
процент → санти (c)
процент → деци (d)
процент → дека (da)
процент → гекто (h)
процент → кило (k)
процент → мега (M)
процент → гига (G)
процент → тера (T)
процент → пета (P)
процент → экза (E)
процент → зетта (Z)
процент → йотта (Y)
процент → ронна (R)
процент → кетта (Q)

Единицы:

кекто
(q)

 /
ронто
(r)

 /
йокто
(y)

 /
цепто
(z)

 /
атто
(a)

 /
фемто
(f)

 /
пико
(p)

 /
нано
(n)

 /
микро
(µ, mc)

 /
милли
(m)

 /
санти
(c)

 /
деци
(d)

 /
дека
(da)

 /
гекто
(h)

 /
кило
(k)

 /
мега
(M)

 /
гига
(G)

 /
тера
(T)

 /
пета
(P)

 /
экза
(E)

 /
зетта
(Z)

 /
йотта
(Y)

 /
ронна
(R)

 /
кетта
(Q)

Частые задачи

Решение
: Пользуемся первым калькулятором. Вводим в первое поле ставку 6, в второе 100000
Получаем 6000 руб. — сумма налога.

Задача 2. У Миши 30 яблок. 6 он отдал Кате. Сколько процентов от общего числа яблок Миша отдал Кате?

Решение:
Пользуемся вторым калькулятором — в первое поле вводим 6, во второе 30. Получаем 20%.

Задача 3. У банка Тинькофф за пополнение вклада из другого банка вкладчик получает 1% сверху от суммы пополнения. Коля пополнил вклад переводом из другого банка на сумму 30 000. На какую итоговую сумму будет пополнен вклад Коли.

Решение
: пользуемся 3м калькулятором. Вводим 1 в первое поле, 10000 во второе. Жмём расчёт получаем сумму 10100 руб.

Самый простой и наглядный метод заключается в составлении пропорции. На ее основе происходят все дальнейшие вычисления. Выглядит это следующим образом:

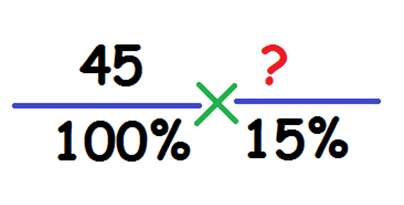
• 45 – известное число, равное 100%.
• ? – число, которое составляет 15% от 45.

Далее, происходит упрощение дроби к уравнению с одной неизвестной. Согласно математическим законам, перекрестные данные в пропорциях равны между собой, то есть: 45*15%=?*100%. Для нахождения «?», пользуемся простым правилом и получаем следующее.

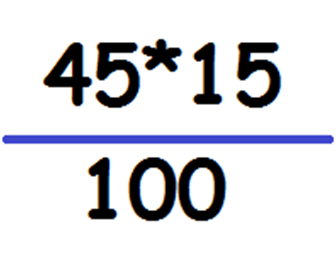
Расчет формулы пропорции всегда происходит по принципу умножения известных данных, стоящих по диагонали и разделением их на третье число.

Можно составить формулу с любым неизвестным в . Что б не путаться, проценты или число получается в результате, вспоминаем правило сокращения в дроби – если знак процента (%) или денежного обозначения (руб) присутствует и сверху и снизу, он сокращается. Пример:

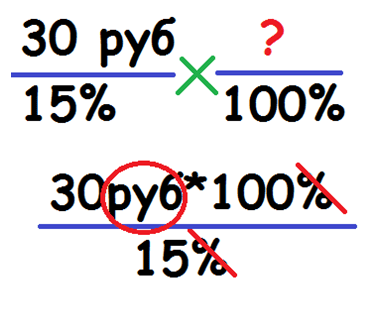
В результате вычисления получается денежная сумма.

Как найти процент от числа. Варианты

Рассмотрим по порядку ситуации по нахождению процентов.

Как найти 100%. Необходимо вычислить число, 15% от которого равно 45. Составляем пропорцию:

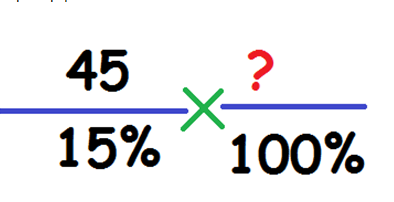
Вычисляем по формуле: (45*100)/15=300

Если не известно, сколько составляет 100%. Иногда расчет проводиться относительно одних и тех же первоначальных данных, но неизвестно их точное значение. К примеру: вчера 15% от общего количества печенья на сумму 450 рублей, а сегодня 25%.

На какую сумму продали сегодня? Так как сумма за 100% является общей величиной и для 15% и для 25%, можно проводить вычисления без поиска полной стоимости.

Вычисляем по формуле: (25*450)/15=750

Можно усложнить задачу, если нет уверенности в расчетах, или возникла потребность проверить результат. Для этого, вначале находиться 100%, на основе полноценных данных (15% стоит 450 рублей), а затем от 100% отсчитывают 25%.