Деление

Смысл деления целых чисел

Мы знаем о существовании связи между умножением и делением натуральных чисел. Из этой связи мы делаем вывод, что деление — это нахождение неизвестного множителя, когда второй множитель и произведение известны. Давайте придадим такое же значение разделению последовательности. Другими словами, деление последовательности — это одно целое число определенного произведения и другой целочисленный множитель.

Исходя из понятия последовательного деления, можно сказать, что если произведение двух целых чисел a и b равно c, то при делении c на a получается b, а при делении c на b — b. Пример. Допустим, мы знаем, что произведение двух целых чисел 5 и -7 равно -35, мы можем сказать, что коэффициент (-35) : 5 равен -7, а коэффициент (-35) : (-7) равен 5.

Обратите внимание, что коэффициент деления целого числа a на целое число b является целым числом (если A делится на B без остатка)

Смысл действия деления

Действие деления рассматривается в начальной школе как действие, обратное умножению.

С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные под-множества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:

а) разбиение множества на равные части (например, 8 кружков разложили в 4 коробки поровну — раскладывают 8 кружков по одному в 4 коробки, а затем считают, сколько кружков получилось в каждой коробке);

б) разбиение множества на части по сколько-то в каждой части (например, 8 кружков разложили в коробки по 4 штуки — раскладывают 8 кружков по 4 штуки в коробки, а затем считают, сколько получилось коробок; деление по этому принципу в методике называют «деление по содержанию»).

Используя подобные предметные действия и рисунки, дети находят результаты деления. Например:

Выражение вида 12 : 6 называют частным.

Число 12 в этой записи называют делимым, а число 6 — делителем.

Запись вида 12 : 6 = 2 называют равенством. Число 2 называют значением выражения. Поскольку число 2 в данном случае получено в результате деления, его также часто называют частным.

Найдите частное чисел 10 и 5. (Частное чисел 10и 5 —это 2.)

Поскольку названия компонентов действия деления вводятся по соглашению (детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания, требующие распознавания компонентов действий и употребления их названий в речи.

1. Среди данных выражений найдите такие, в которых делитель равен 3:

2:2 6:3 6:2 10:5 3:1 3-2 15:3 3-4

2. Составьте частное, в котором делимое равно 15. Найдите его значение.

3. Выберите примеры, в которых частное равно 6. Подчеркните их красным цветом. Выберите примеры, в которых частное равно 2. Подчеркните их синим цветом.

4. Как называют число 4 в выражении 20 : 4? Как называют число 20? Найдите частное. Составьте пример, в котором частное равно тому же числу, а делимое и делитель — другие.

5. Делимое 8, делитель 2 . Найдите частное.

В 3 классе дети знакомятся с правилом взаимосвязи компонентов деления, которое является основой для обучения нахождению неизвестных компонентов деления при решении уравнений:

Если делитель умножить на частное, то получится делимое.

Если делимое разделить на частное, то получится делитель. ₍

Решите уравнение 16 : х= 2. (В уравнении неизвестен делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. х = 16 : 2, х = 8.)

Однако, данные правила в учебнике математики 3 класса не являются обобщением представлений ребенка о способах проверки действия деления. Правило проверки результатов деления рассматривается в учебнике после знакомства с внетабличным умножением и делением (знакомства с умножением и делением двузначных чисел на однозначные, не входящим в таблицу умножения и деления), перед последним самым трудным случаем вида 87 : 29. Это объясняется тем, что получение результатов деления в этом случае представляет собой сложный процесс подбора частного с постоянной его проверкой умножением, поэтому правило проверки действия деления дети рассматривают даже раньше, чем правило проверки действия умножения.

Правило проверки действия деления:

1) Частное умножают на делитель.

2) Сравнивают полученный результат с делимым. Если эти числа равны, деление выполнено верно.

Например: 78 : 3 = 26. Проверка: 1) 26 • 3 — 78; 2) 78 — 78.

Источник

Как делить числа с остатком?

Prostock-studio/Shutterstock.com

Деление с остатком выполняется точно так же, как и любое другое деление; но в результате, помимо частного, мы получаем ещё и остаток, который всегда меньше делителя. Как объяснить это ребёнку? Приведите в пример любую покупку в магазине за наличные.

Допустим, ребёнок отправляется в пекарню за булочками; вы даёте ему 400 рублей, при этом одна булочка стоит 38 рублей. Вычислим, сколько булочек к завтраку и какую сдачу принесёт ваш ребёнок:

Первое неполное делимое — 40 — делится на 38 и даёт нам цифру 1 в частном; к оставшейся цифре 2 (40–38=2) сносим оставшийся от делимого 0. Но получившееся число 20 на 38 не делится нацело, поэтому в частном мы пишем 0, а 20 записываем в остаток:

400 ÷ 38 = 10 (ост. 20)

Таким образом, взяв с собой 400 рублей, ваш школьник принесёт домой 10 булочек по 38 рублей за каждую и 20 рублей сдачи.

Конечно, для двузначных чисел в пределах таблицы умножения применять деление в столбик не нужно: ответ можно найти путём подбора. Разберём пример:

53 ÷ 6 = ?

Здесь нужно вспомнить таблицу умножения на 6. Ближайшее к делимому 53 число, которое мы получаем при умножении 6 на 8 — 48. Далее необходимо вычислить остаток:

53 – 48 = 5

5<6, соответственно, мы правильно вычислили остаток (помним, что он не должен быть равен или больше делителя). Запишем ответ таким образом:

53 ÷ 6 = 8 (ост. 5)

Деление на ноль[править | править код]

По определению числовых множеств N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } деление на число 0 не определено. Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного. Для определения данной ситуации полагают, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов). С геометрической точки зрения выполняется аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел «сжимается» так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины +∞,−∞{\displaystyle +\infty ,-\infty }. С точки зрения общей топологии выполняется двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком). Пишут:

Топологическая картинка проективного расширения числовой прямой и точки 0/0

a=±∞{\displaystyle a:0=\pm \infty }, где a≠{\displaystyle a\neq 0.}

Если произвести проективное расширение множества вещественных чисел введением идеализированной точки ∞ {\displaystyle \infty ~},которая соединяет оба конца вещественной прямой, тогда с точки зрения общей топологии будет выполнена числовой прямой путем добавления бесконечности без знака. Дополним полученное множество чисел новым элементом ⊥={\displaystyle \perp =0/0}, в результате получится R⊥∞=R∪{∞,⊥}{\displaystyle \mathbb {R} _{\perp }^{\infty }=\mathbb {R} \cup \{\infty ,\perp \}}, на данной основе строится алгебраическая структура W=⟨R⊥∞,,1,+,⋅,⟩ {\displaystyle {\mathfrak {W}}=\langle \mathbb {R} _{\perp }^{\infty },0,1,+,\cdot ,/\rangle ~}называемая «Колесом» (Wheel). Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0. Внесенные изменения превращают эту алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента). Это тип алгебры, где деление всегда определено. В частности, деление на ноль имеет смысл.

Существуют и другие алгебраические системы с делением на ноль. Например, «общие луга» (common meadows). Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а также отказом от бинарного деления.

Свойства[править | править код]

Операция деления на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } имеет следующие основные свойства:

Деление не перестановочно (не коммутативно) — от перемены мест аргументов частное изменяется:

ab≠ba;{\displaystyle a:b\neq b:a;}

Деление не ассоциативно — при последовательном выполнении деления трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:

(ab)c≠a(bc);{\displaystyle (a:b):c\neq a:(b:c);}

Деление дистрибутивно справа, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон :

Дистрибутивность: (a+b)x=(ax)+(bx), x≠;{\displaystyle (a+b):x=(a:x)+(b:x),~x\neq 0;}

Относительно деления в множестве A{\displaystyle A} существует единственный нейтральный элемент справа (число 1{\displaystyle 1}), деление на единицу (или нейтральный элемент) даёт число, равное исходному:

Нейтральный элемент справа: x1=x;{\displaystyle x:1=x;}

Относительно деления в множестве A{\displaystyle A} существует единственный обратный элемент, получаемый делением единицы на число, что даёт число, обратное исходному:

Обратный элемент: 1x=1x=x−1, x≠;{\displaystyle 1:x={\frac {1}{x}}=x^{-1},~x\neq 0;}

Относительно деления в множестве A{\displaystyle A} существует единственный нулевой элемент слева — число 0{\displaystyle 0}, делённое на любое число, даёт нуль:

Нулевой элемент слева: x=,∃∈A, x≠;{\displaystyle 0:x=0,\quad \exists 0\in A,~x\neq 0;}

По правилам обычной арифметики деление на ноль 0{\displaystyle 0} (нулевой элемент) не определено;

Деление на ноль: x=∞,∃∈A, x≠;{\displaystyle x:0=\infty ,\quad \exists 0\in A,~x\neq 0;}

Деление на противоположный элемент даёт минус единицу:

x(−x)=−1,∃!−x∈A, x≠{\displaystyle x:(-x)=-1,\quad \exists !-x\in A,~x\neq 0.}

Результат деления не всегда является определённым для множеств натуральных чисел N{\displaystyle \mathbb {N} } и целых чисел Z{\displaystyle \mathbb {Z} }, чтобы получить натуральное или целое число в результате деления, делимое должно быть кратно делителю. Невозможно в рамках этих чисел получить дробный результат. В этом случае говорится о делении с остатком. То есть деление на этих множествах есть частичная бинарная операция.

Операция деления, определённая на множествах (в полях) рациональных Q{\displaystyle \mathbb {Q} }, вещественных R{\displaystyle \mathbb {R} } и комплексных чисел C{\displaystyle \mathbb {C} }, даёт число (частное), принадлежащее этому же множеству, следовательно, множества Q−,R−,C−{\displaystyle \mathbb {Q_{-0}} ,\mathbb {R_{-0}} ,\mathbb {C_{-0}} } замкнуты относительно операции деления (в точке 0 имеется разрыв второго рода — следовательно кольца рациональных, вещественных и комплексных чисел разомкнуты относительно операции деления).

В математических выражениях операция деления имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.

Объясняем ребёнку правила деления

Fabio Principe/Shutterstock.com

Бывает, что беглой презентации новой темы во время школьного урока оказывается недостаточно для её понимания, и ваш третьеклассник идёт за разъяснениями к вам. Начните с объяснения ключевых понятий:

• деление — это действие, которое позволяет разбить какое-либо число на равные части. Иногда это возможно, иногда нет, и в последнем случае в результате деления образуется остаток. Приводите наглядные примеры: разделить шесть яблок на семью из трёх человек можно без труда, а вот четыре банана — уже сложнее: один банан останется;
• делимое — то число, которое нам необходимо разделить. В случае с яблоками — 6, а в примере с бананами — 4;
• делитель — число, на которое мы будем делить. В нашем случае — 3;
• частное — результат деления: каждому члену семьи достанется по два яблока и по одному банану.

Теперь переходим к основным правилам деления.

Правило 1

Деление — операция, противоположная умножению. Для деления на однозначные числа порой достаточно уверенного знания таблицы умножения: нужно просто «перевернуть» пример с делением и вспомнить нужную строчку из таблицы умножения.

Пусть ребёнок представит, что хочет угостить друзей конфетами, но не может разделить их поровну; всего в пакете 25 конфет, а ребят — пятеро:

25 ÷ 5 = ? → ? × 5 = 25 → Ответ: 5 конфет каждому.

Правило 2

Когда в качестве делимого выступает большее число, чем встречается в таблице умножения, для удобства мы разбиваем его на сумму из двух или трёх слагаемых и каждое делим по отдельности; сумма всех частных и будет ответом:

96 ÷ 4 = (40 + 40 + 16) ÷ 4 = (40 ÷ 4) + (40 ÷ 4) + (16 ÷ 4) = 10 + 10 + 4 = 24

Правило 3

При делении круглых чисел (оканчивающихся на 0) на другие круглые числа для удобства мы отбрасываем одинаковое количество нулей у делимого и делителя:

400 ÷ 80 = 40 ÷ 8 = 5

При делении круглого числа на однозначное операция выполняется без учёта нулей в конце делимого, а нули просто приписываются к полученному частному:

4200 ÷ 6 = ? → 42 ÷ 6 = 7 → 4200 ÷ 6 = 700

Существует также несколько базовых правил:

• делить на 0 нельзя;
• при делении на 1 делимое равно частному;
• если делимое и делитель одинаковые, частное равно 1;
• если делимое равно 0, то и частное будет равно 0.

Деление физических величин[править | править код]

Единица измерения физической величины имеет определённое наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции деления. При производстве операции деления над физическими величинами, делятся как сами числовые составляющие, так и их наименования.

Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определённым физическим явлениям (измеряются «штуками», «разами» и тому подобное). При делении чисел представляющих собой физические величины на безразмерную величину, делимое число изменяется по величине и сохраняет единицу измерения. Например если взять 15 гвоздей и разложить в 3 коробки, то в результате деления получим 5 гвоздей в каждой коробке:

15 гв3=5 гв.{\displaystyle 15~{\text{гв}}:3=5~{\text{гв}}.}

Деление разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы делим. Если физически возможно создание такого частного, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее.

Например, если разделить длину L=8 м {\displaystyle L=8~{\text{м}}~}на время T=2 с, {\displaystyle T=2~{\text{с}},~}соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «скорость» и измеряется в «метрах в секунду»: V=4 м/с.{\displaystyle V=4~{\text{м/с}}.}

V=LT=8 м2 с=4  (м : с)=4 м/с.{\displaystyle V=L:T=8~{\text{м}}:2~{\text{с}}=4~~{\text{(м : с)}}=4~{\text{м/с}}.}

При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно и не могут быть непосредственно разделены. Также понятие однородности предполагает, что делимые величины принадлежат одному физическому процессу. Недопустимо делить, например скорость лошади на время собаки.

Деление на 10, 100, 1 000 и т.д.

Сразу дадим формулировку правила деления натуральных чисел на 10, 100, 1 000, … (будем считать, что такое деление возможно) и приведем пример, а потом приведем необходимые разъяснения.

Результатом деления натурального числа на 10, 100, 1 000 и т.д. является натуральное число, запись которого получается из записи делимого, если справа отбросить один, два, три и так далее нулей (то есть, отбрасывается столько цифр , сколько их содержится в записи делимого).

Например, частное от деления числа 30 на 10 равно 3 (от делимого 30 справа отбросили одну цифру ), а частное 120 000:1 000 равно 120 (от 120 000 справа убрали три цифры ).

Озвученное правило достаточно просто обосновать. Для этого достаточно вспомнить Приведем пример. Пусть нам требуется вычислить частное 10 200:100. Так как 102·100=10 200, то в силу связи между сложением и умножением результатом деления натурального числа 10 200 на 100 является натуральное число 102.

Связь деления с умножением

Давайте проследим связь между делением и умножением. Для этого вспомним, что деление связано с представлением множества, которое мы делим, в виде объединения нескольких одинаковых множеств, на которые мы делим исходное множество (об этом мы говорили в разделе ). В свою очередь умножение связано с объединением некоторого количества одинаковых множеств в одно (при необходимости обращайтесь к разделу теории ). Таким образом, деление является действием, обратным к умножению.

Поясним, что же означает последняя фраза.

Для этого рассмотрим следующую ситуацию. Пусть мы имеем b множеств по c предметов в каждом, и мы объединяем их в одно множество, в котором получается a предметов. На основании можно утверждать, что описанному действию отвечает равенство c·b=a. Теперь полученное множество вновь разделим на b одинаковых множеств. Понятно, что при этом в каждом полученном множестве будет c предметов. Тогда, вспомнив , можно записать равенство a:b=c.

Приходим к следующему утверждению: если произведение натуральных чисел c и b равно a, то частное от деления a на b равно c.

Итак, если c·b=a, то a:b=c. Однако в силу мы можем равенство c·b=a переписать в виде b·c=a, откуда следует, что a:c=b. Таким образом, если мы знаем, что произведение двух натуральных чисел с и b равно a, то есть, c·b=a, то мы можем сказать, что частные a:b и a:c равны c и b соответственно.

На основании всей приведенной информации можно дать определение деления натуральных чисел на основе умножения.

Определение.

Деление – это действие, с помощью которого находится один множитель, когда известно произведение и другой множитель.

На базе этого определения мы и будем строить правила деления натуральных чисел.

Основные приемы при делении

Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.

Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.

Чтобы разделить 27 на 3 мы пишем

Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.

Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.

Само вычисление выражают письменно:

Деление совершилось нацело.

Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.

Отыскивая целое частно, мы имеем при этом три случая:

1. Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:

   в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.

2. Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.

3. Взяв для частного 6, мы ход вычисления выражаем письменно:

   словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:

Правило определения частного:

1. Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.

2. Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.

3. Если остаток меньше делителя, цифра частного верна.

Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.

В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и

27 = 4 × 6 + 3 = 24 + 3

Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.

Продвинутое применение

Деление по модулю может быть полезно не только в простых математических вычислениях, но и в более сложных задачах программирования.

Например, при работе с графами и поиском путей, деление по модулю может помочь определить номер вершины, если все вершины представлены числами от 0 до n-1. В таких случаях деление по модулю n может быть использовано для получения номера вершины, который будет меньше или равен n-1.

Другим примером использования деления по модулю является генерация случайных чисел. Используя деление по модулю и некоторую константу, можно получить последовательность псевдослучайных чисел, которая будет иметь некоторые хорошие свойства. Например, такая последовательность может быть равномерной и не содержать корреляции между соседними числами.

Также деление по модулю может быть использовано для работы с циклическими структурами данных, например, кольцевыми буферами. При добавлении нового элемента в кольцевый буфер, можно использовать деление по модулю размера буфера для определения позиции, в которую нужно записать элемент. А при чтении элементов из буфера, также можно использовать деление по модулю для определения следующей позиции для чтения.

Деление по модулю также может быть использовано в алгоритмах шифрования. Например, в одном из алгоритмов шифрования деление по модулю используется для того, чтобы распределить часть ключа на разные позиции в тексте сообщения. Это делает шифрование более надежным и сложным для взлома.

• Выводы
• В контексте программирования, деление по модулю может быть использовано для различных задач, таких как работа с графами, генерация случайных чисел, работа с кольцевыми буферами и алгоритмы шифрования.
• Правильное использование деления по модулю помогает в улучшении производительности и безопасности программ.

Работа с большими числами

Деление по модулю в Python может быть непригодным для работы с большими числами. В случае, если требуется работать с числами, которые выходят за пределы стандартных типов данных, таких как int или float, необходимо использовать специальные библиотеки.

Одна из таких библиотек – это библиотека gmpy2, которая предоставляет функции для работы с числами произвольной длины. С ее помощью можно выполнить как простые математические операции, так и более сложные алгоритмы.

Кроме того, существуют и другие библиотеки, такие как pycrypto или cryptography, которые также позволяют работать с большими числами и выполнять криптографические операции.

При работе с большими числами необходимо учитывать, что они могут занимать большой объем памяти и требовать большой вычислительной мощности. Поэтому, для достижения максимальной производительности, рекомендуется использовать специализированные библиотеки и оптимизировать код с учетом особенностей работы с большими числами.

В заключение, работа с большими числами может быть иногда необходима при решении сложных математических задач или криптографических алгоритмов. Для этого следует использовать специальные библиотеки и учитывать особенности работы с данными типами чисел.

Использование в алгоритмах шифрования

Деление по модулю широко используется в алгоритмах шифрования для обеспечения безопасности передаваемых данных. Одним из таких алгоритмов является RSA-шифрование.

В алгоритме RSA для шифрования используются два простых числа — p и q, из которых вычисляется произведение N = p*q. Затем выбирается число e, которое является взаимно простым с функцией Эйлера от числа N. После этого находится число d, обратное по модулю функции Эйлера от N, к числу e.

Для шифрования сообщения M, преобразуется в число m, меньшее N, и вычисляется c = m^e mod N. Для расшифровки сообщения используется формула m = c^d mod N. В этом случае деление по модулю позволяет сократить результаты возведения в степень, что значительно ускоряет процесс расшифровки.

Также, деление по модулю используется в симметричных алгоритмах шифрования, например, в алгоритме XOR. В этом случае, для шифрования каждого байта сообщения, используется ключ — случайное число, которое применяется по модулю 256.

Применение в математике и программировании

Понятия делимого, частного и остатка широко применяются в математике и программировании.

В математике, деление является одной из основных операций, выполняемых с числами. Отношение делимого к делителю называется частным, а остаток — это любое число, которое остается после выполнения деления без остатка.

Применение концепции деления в программировании неотъемлемо во многих областях, начиная от арифметических вычислений и заканчивая алгоритмами и структурами данных.

Например, в арифметических вычислениях, деление используется для решения задач, связанных с поиском среднего значения, определением процентов, долей и других подобных операций.

В программировании, понимание деления и операций с остатком критически важно при работе с массивами, списками и другими структурами данных. Например, при поиске элементов в массиве, остаток от деления может использоваться для определения четности или нечетности числа или для определения принадлежности к определенному диапазону

Также, понимание деления помогает в оптимизации кода и разработке эффективных алгоритмов. Знание особенностей деления нацело и использование остатка помогает улучшить производительность программ и упростить их реализацию.

В общем, понятия делимого, частного и остатка имеют фундаментальное значение в математике и программировании и широко применяются для решения различных задач и проблем.

Деление в алгебре[править | править код]

В отличие от простейших арифметических случаев, на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым (x−1∗x=e{\displaystyle x^{-1}*x=e}), так и правым (x∗x−1=e{\displaystyle x*x^{-1}=e}). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

B−1⋅A≠A⋅B−1{\displaystyle B^{-1}\cdot A\neq A\cdot B^{-1}}.

Отношение тензоров в общем случае не определено.

Приемы умножения и деления с числом 10

Маша решает примеры. Давайте понаблюдаем, как она рассуждает.

2 ∙ 10 =

10 ∙ 2 =

20 : 10 =

20 : 2=

Ребята, у меня есть 2 коробки цветных карандашей. В каждой коробке по 10 штук. Сколько всего цветных карандашей в этих коробках?

Решение можно записать сложением 10 + 10 = 20. Мы видим, что по 10 взяли два раза. А это значит: 10 ∙ 2 = 20. Зная переместительное свойство умножения, запишем: 2 ∙ 10 =20.

Еще одно важное правило нужно вспомнить:

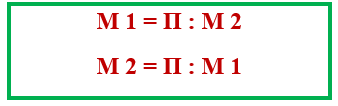
Пользуясь им, составим два примера на деление.

20 : 10 = 2

20 : 2= 10

Вот так Маша! Молодец! С заданием справилась на отлично. Попробуйте и вы, ребята, так же рассуждать. Решите примеры.

3 ∙ 10 =

10 ∙ 3 =

30 : 10 =

30 : 3=

Проверь себя.

3 ∙ 10 = 30

10 ∙ 3 = 30

30 : 10 = 3

30 : 3= 10

Мишка знает еще один способ решения примеров с числом 10.

Посмотрите внимательно на этот пример:

При умножении числа на 10 не забудь справа приписать к числу нуль.

Если же число делишь на 10, не забудь от этого числа отбросить нуль.

Какой способ вам понравился больше: тот, которым решала Маша или Мишин совет?

Выбирайте любой способ, будем соревноваться с Машей и Мишей решать примеры на время! Дается всего одна минута. Примеры записывать не нужно, пишите только ответы через запятую. Попросите друга напомнить, когда минута закончится.

Итак, начинаем!

Маша решила без ошибок, но времени на все примеры не хватило, осталось решить еще 2 примера. Миша решил все примеры без ошибок. Хороший результат! А как вы справились с заданием?

Напоследок Маша подготовила для вас, ребята, задачу на смекалку. Не торопитесь, хорошо подумайте!

Когда Мишка в своем домике находится без головы? Посмотрите на рисунок, думаю, он вам поможет дать правильный ответ

Правильный ответ: Миша будет находиться в своем домике без головы, если выглянет в окно. Голова-то будет на улице, а не в доме!

Нам еще многому предстоит научиться. А сегодняшний урок подошел к концу. Проверьте, как вы запомнили Мишины советы, все ли поняли.

Нахождение элементов деления

В примере$$\textcolor{purple}{30}:\textcolor{coral}{3}=\textcolor{lightblue}{10}$$$30$ — это $\textcolor{purple}{делимое}$, $3$ — $\textcolor{coral}{делитель}$, а $10$ — $\textcolor{lightblue}{частное}$. Давайте разберем на данном примере, как находить каждый элемент деления.

Чтобы найти неизвестное $\textcolor{purple}{делимое}$, надо $\textcolor{lightblue}{частное}$ умножить на $\textcolor{coral}{делитель}$.$$\textcolor{purple}{x}:\textcolor{coral}{3}=\textcolor{lightblue}{10} \newline \textcolor{purple}{x}=\textcolor{lightblue}{10}\cdot \textcolor{coral}{3}\newline \textcolor{purple}{x}=30$$

Чтобы найти неизвестный $\textcolor{coral}{делитель}$, надо $\textcolor{purple}{делимое}$ разделить на $\textcolor{lightblue}{частное}$.$$\textcolor{purple}{30}:\textcolor{coral}{x}=10 \newline \textcolor{coral}{x}=\textcolor{purple}{30}:\textcolor{lightblue}{10} \newline \textcolor{coral}{x}=3$$

А теперь вернемся немного назад к теме «Умножение» и определим, как искать неизвестный множитель на примере: $3\cdot10=30$

Для того чтобы найти $\textcolor{orange}{неизвестный\spaceмножитель}$, нужно $\textcolor{green}{произведение}$ разделить на $\textcolor{blue}{другой\spaceмножитель}$.$$\textcolor{orange}{x}\cdot \textcolor{blue}{10}=\textcolor{green}{30} \newline \textcolor{orange}{x}=\textcolor{green}{30}:\textcolor{blue}{10} \newline \textcolor{orange}{x}=3$$

{"questions":,"answer":}},"step":1,"hints":}]}

Представление делимого в виде разности двух натуральных чисел

Иногда делимое проще представить в виде разности двух натуральных чисел, чем в виде суммы, что значительно ускоряет процесс деления. Разберемся с этим на примере.

Пример.

Разделите 594 на 6.

Решение.

Несомненно, мы можем воспользоваться алгоритмом из предыдущего пункта, по которому делимое 594 представляется в виде суммы 540+54. При этом мы получим 594:6=(540+54):6=540:6+54:6=90+9=99.

Но проще поступить немного иначе. Несложно видеть, что делимое 594 можно представить в виде разности 600−6, причем натуральные числа 600 и 6 легко делятся на 6. Тогда 594:6=(600−6):6. Теперь по полученное частное (600−6):6 равно разности 600:6−6:6, которая очень легко вычисляется: 600:6−6:6=100−1=99.

Ответ:

594:6=99.

Разберем решение еще одного примера.

Пример.

Вычислите частное 483:7.

Решение.

Натуральное число 483 удобно представить в виде разности 490−7, в которой и уменьшаемое и вычитаемое легко делятся на 7. Получаем 483:7=(490−7):7=490:7−7:7=70−1=69.

Ответ:

483:7=69.

Примеры на деление уголком для начальной школы

Проверьте, насколько хорошо ребёнок усвоил деление столбиком, предложив ему решить эти примеры:

Третий класс	Четвёртый класс
Лёгкий уровень 72:3= 48:4= 39:5= 84:6= Средний уровень 105:5= 645:5= Сложный уровень 968:4= 728:8= 87:29= 228:19=	Лёгкий уровень 5 922:9= 8 556:4= 15 395:5= Средний уровень 76 128:8= 10 000:200= 15 000:75= Сложный уровень 18 200:26= 4 057:35= 784:23= 8 591:62=
Ответы
Лёгкий уровень 24, 12, 7 (ост. 4) Средний уровень 14, 21, 129 Сложный уровень 242, 91, 3, 12	Лёгкий уровень 658, 2 139, 3 079 Средний уровень 9 516, 50, 200 Сложный уровень 700, 115 (ост. 32), 34 (ост. 2), 138 (ост. 35)

⠀

Обучение делению в столбик — нелёгкая задача, особенно для тех родителей, которые далеки от точных наук и педагогики. Начинайте с простых примеров и постепенно наращивайте сложность, а главное — убедитесь в том, что ребёнок отлично знает таблицу умножения. Решайте как можно больше примеров, приводите примеры применения новых знаний в повседневной жизни и поддерживайте вашего школьника — тогда всё обязательно получится!

Источник фото обложки: fizkes/Shatterstock.com

Деление натуральных чисел, записи которых оканчиваются цифрами 0

Здесь нам потребуется вспомнить . Поясним, для чего. Чтобы выполнить деление натуральных чисел, записи которых оканчиваются цифрами , делитель представляется в виде произведения двух натуральных чисел, после чего применяется упомянутое свойство деления.

Разберемся с этим на примерах. Возьмем два натуральных числа, записи которых оканчиваются цифрами ноль, и разделим их.

Пример.

Разделим 490 на 70.

Решение.

Так как 70=10·7, то 490:70=490:(10·7). Последнее выражение в силу свойства деления натурального числа на произведение равно (490:10):7. Делить на 10 мы научились в одном из предыдущих пунктов, получаем (490:10):7=49:7. Полученное частное находим по таблице умножения, в итоге получаем 490:70=7.

Ответ:

490:70=7.

Для закрепления материала рассмотрим решение еще одного более сложного примера.

Пример.

Вычислим частное 54 000:5 400.

Решение.

Представляем 5 400 в виде произведения 100·54 и выполняем деление натурального числа на произведение: 54 000:5 400=54 000:(100·54)=(54 000:100):54=540:54. Здесь осталось представить 540 как 54·10 (при необходимости вернитесь к предыдущему пункту) и закончить вычисления: 540:6=(54·10):54=(54:54)·10=1·10=10. Итак, 54 000:5 400=10.

Ответ:

54 000:5 400=10.

Информацию этого пункта можно подытожить следующим утверждением: если в записи и делимого и делителя справа находятся цифры , то в записях нужно избавиться от одинакового количества крайних справа нолей, после чего выполнить деление полученных чисел. Например, деление натуральных чисел 818 070 000 и 201 000 сводится к делению чисел 818 070 и 201 после того, как мы в записях делимого и делителя справа уберем по три цифры .