Задачи на прогрессии

Решение задач на геометрическую прогрессию

Рассмотрим несколько типичных задач, посвященных геометрической прогрессии.

Задача 1:

Дана геометрическая прогрессия 3, 6, 12, … . Найти 8-ой член геометрической прогрессии и сумму первых 10 членов.

Решение:

b1 = 3

q = 6 / 3 = 2

b8 = b1 ⋅ q7 = 3 ⋅ 27 = 3 ⋅ 128 = 384

S10 = b1 ⋅ (1 — q10) / (1 — q) = 3 ⋅ (1 — 210) / (1 — 2) = 3 ⋅ (1 — 1024) / (–1) = 3069

Ответ: 384 и 3069

Задача 2:

Число 486 является членом геометрической прогрессии 2, 6, 18, … . Найдите его номер.

Решение:

b1 = 2

q = 6 / 2 = 3

Применив формулу для вычисления n-ого члена геометрической прогрессии, можно получить n:

486 = 2 ⋅ 3n — 1

243 = 3n — 1

35 = 3n — 1

n — 1 = 5

n = 6

Ответ: 6

Задача 3:

Сумма n первых членов геометрической прогрессии равна –93. b1 = –3, q = 2. Найти n.

Решение:

Чтобы вычислить число членов геометрической прогрессии, можно воспользоваться формулой ее суммы:

Sn = b1 ⋅ (1 — qn) / (1 — q)

–93 = –3 ⋅ (1 — 2n) / (1 — 2)

–93 = –3 ⋅ (1 — 2n) / (–1)

–31 = 1 — 2n

2n = 32

n = 5

Ответ: 5

Определение геометрической прогрессии

Математически геометрическую прогрессию можно записать следующим образом:

a, a * q, a * q2, a * q3, …

Где:

• a — первый элемент прогрессии;
• q — знаменатель прогрессии.

Например, рассмотрим прогрессию:

2, 4, 8, 16, 32, …

Здесь первый элемент прогрессии a = 2, а знаменатель прогрессии q = 2. Последующие элементы прогрессии получаются путем умножения предыдущего элемента на знаменатель: 2 * 2 = 4, 4 * 2 = 8 и т.д.

Геометрическая прогрессия имеет широкое применение в различных областях, таких как финансы, физика, информатика и др. Ее свойства и закономерности помогают в решении различных задач, а также являются основой для изучения других важных понятий в математике.

Примеры решения задач

Задача № 1

Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.

Найти знаменатель и первый член геометрической прогрессии.

Решение:

По условиям задачи:

\(b_1+b_1q^2=35.,\)

\(b_1\left(1+q+q^2+q^3+q^4\right)=49\left(\frac1{b_1}+\frac1{b_1q}+\frac1{b_1q^2}+\frac1{b_1q^3}+\frac1{b_1q^4}\right).\) (2)

Так как \(1+q+q^2+q^3+q^4\neq0\) (иначе задача теряет смысл), то равенство (2) можно записать в виде:

\(b_1^2q^4=49. \) (3)

Из (3) следует, что либо \(b_1q^2=7,\) либо \(b_1q^2=-7.\)

Если равно 7, то из (1) находим \(b_1=28,\) \(q^2={\textstyle\frac14}\), откуда \(q=\pm\frac12\ \)

Если равно -7, \(b_1=42,\) \(\\q^2=-{\textstyle\frac16}\). В этом случае второе условие задачи теряет смысл. 

Конечный результат:

\(b_1=28,\) \(q=\pm\frac12. \)

Задача № 2

\(S_n\) — сумма первых n членов геометрической прогрессии.

Доказать, что: \(S_n\left(S_{3n}-S_{2n}\right)=\left(S_{2n}-S_n\right)^2\). (1)

Доказательство:

Пусть \(b_k — k-й\) член, \(q\)— знаменатель геометрической прогрессии. Тогда:

\(S_{m+k}=S_m+b_1q^m+b_1q^{m+1}+…+b_1q^{m+k-1},\)

откуда:

\(S_{m+k}-S_m=q^m\left(b_1+b_1q+…+b_1q^{k-1}\right)\)

или

\(S_{m+k}-S_m=q^mS_k\) (2).

Полагая в (2) сначала \(m = 2_n,\) \(k = n\), а затем \(m = n\), \(k = n\), получаем

\(S_{3n}-S_{2n}=q^{2n}\cdot S_n\), \(S_{2n}-S_n=q^n\cdot S_n.\) (3)

А из равенств (3) следует равенство (1).

Задача № 3

Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.

Найти первый член и знаменатель этой прогрессии.

Решение:

Обозначим: \(b_1\) — первый член, \(S\) — сумма прогрессии, \(q\) — знаменатель, \(S_1\) — сумма возведенных в третью степень ее членов.

Тогда

\(S=\frac{b_1}{1-q}\),\( S_1=\frac{b_1^3}{1-q^3}.\)

Далее получаем

\(\frac{S^3}{S_1}-\frac{1-q^3}{{(1-q)}^3}=\frac{4^3}{192}=\frac13\ \)

\(3(1+q+q^2)=1-2q+q^2,\;q\neq1..\)
Полученное уравнение, записанное в виде

\(2q^2+5q+2=0\)

имеет корни \(q_1 = −2,\) \(q_2 = − ½.\)

Так как \(|q| < 1\), отбрасываем первый корень.

Следовательно:

\(q=-\frac12,\;b_1=4(1-q)=6.\)

Задача № 4

\(S_n\)первых трех членов геометрической прогрессии равна 351. \(S_n\) следующих трех членов равна 13.

Найти первый член и знаменатель прогрессии.

Решение:

Запишем условия задачи в виде системы уравнений:

\(\left\{\begin{array}{l}b_1+b_2+b_3=351,\\b_4+b_5+b_6=13\end{array}\right.\Leftrightarrow\ \left\{\begin{array}{l}b_1+b_1q+b_1q^2=351,\\b_1q^3+b_1q^4+b_1q^5=13\end{array}\right.\Leftrightarrow\ \left\{\begin{array}{l}b_1(1+\frac13+\frac19)=351,\\q=\frac13\end{array}\right.\Leftrightarrow\left\{\begin{array}{l}\frac{13}9b_1=351,\\q=\frac13\end{array}\Leftrightarrow\left\{\begin{array}{l}b_1=\frac{351\cdot9}{13}=243,\\q=\frac13.\end{array}\right.\right..\)

Ответ: \(b_1=243,\;q=\frac13.\)

Задача № 5

Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.

Найти знаменатель прогрессии?

Решение:

Определим, что в прогрессии 2n членов и \(S_{2n}\) — сумма всех членов, а \(S_n^\ast\) — сумма членов, стоящих на нечетных местах.

Тогда \(S_{2n}=\frac{b_1(1-q^{2n})}{1-q}.\)

И 

\(S_n^\ast=b_1+b_3+…+b_{2n-1}=b_1+b_1q^2+…+b_1q^{2n-2}=\frac{b_1(1-q^{2n)}}{1-q^2}.\)

Где \(b_1\) — первый член прогрессии, а \(q ≠ 1\) — знаменатель прогрессии.

По условию задачи:

\(S_{2n}=3S_n^\ast\Rightarrow\frac{b_1(1-q^{2n)}}{`1-q}=3\frac{b_1(1-q^{2n)}}{1-q^2}\Rightarrow1+q=3\Rightarrow q=2.\)

Формулы

Для удобного использования геометрических прогрессий существует множество формул:

Формула z-го члена. Позволяет рассчитать элемент, стоящий под конкретным номером без расчета предыдущих чисел.

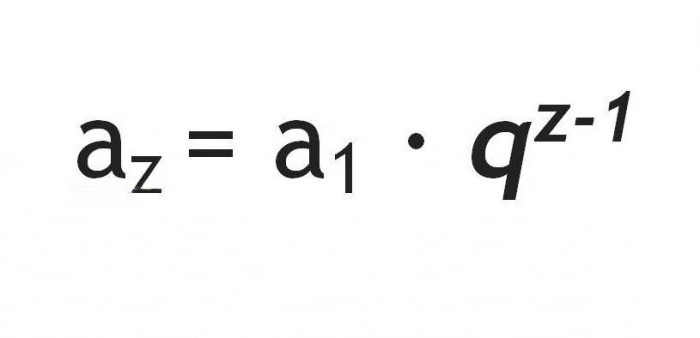
Пример:


q


= 3,


a


1


= 4. Требуется посчитать четвертый элемент прогрессии.

Решение:


a


4


= 4

·

3 4-1 = 4

·

3 3 = 4

·

27 = 108.

Сумма первых элементов, чье количество равно

z

. Позволяет рассчитать сумму всех элементов последовательности до

a z

включительно.

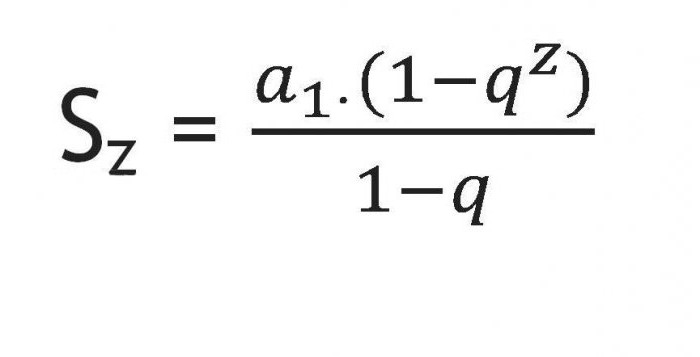
Так как (1-


q


) стоит в знаменателе, то (1 — q)

≠ 0, следовательно, q не равно 1.

Замечание: если бы q=1, то прогрессия представляла бы собой ряд из бесконечно повторяющегося числа.

Сумма геометрической прогрессии, примеры:


a


1


= 2,


q


= -2. Посчитать S 5 .

Решение:


S


5 =


22 — расчет по формуле.

Сумма, если |

q

|

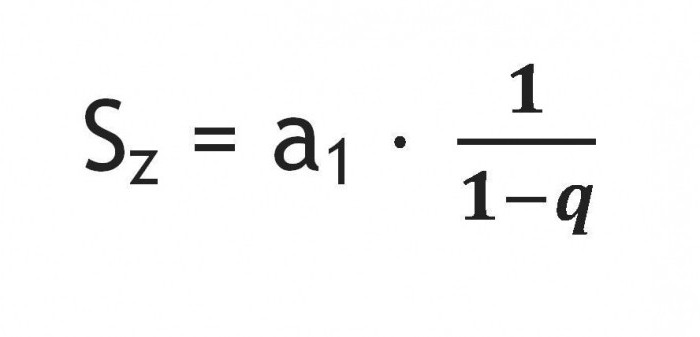
Пример:


a


1


= 2 ,


q


= 0.5. Найти сумму.

Решение:


S z


= 2


·


= 4

S z


= 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375


4

Что такое геометрическая прогрессия?

Возьмите лист бумаги и сложите его столько раз, сколько сможете. Какая получилась толщина бумаги после этого? И как это определить? Ответом будет геометрическая прогрессия. В ней последующее число в серии является двойным по сравнению с предыдущим числом.

Другими словами, когда 1 умножается на 2, получается 2. Когда 2 умножается на 2, получается 4. Точно так же, когда 4 умножается на 2, мы получаем 8 и так далее. Можно ли сказать, что соотношение двух следующих друг за другом членов геометрического ряда постоянно? 

Таким образом, соотношение двух последовательных членов этой конкретной последовательности является фиксированным числом. Такая последовательность чисел называется геометрической прогрессией (ГП).

Кроме того, первый член не равен нулю, а каждый последующий член получается путем умножения предыдущего члена на фиксированную величину. К примеру, рассмотрим последовательность 1, 2, 4, 8, 16, 32… . Здесь общее отношение r=2 – это знаменатель геометрической прогрессии. 

Знание прогрессии и умение проводить необходимые вычисления чрезвычайно полезно в самых различных отраслях деятельности.

Например, в строительстве определение площади поперечного сечения колонн, равномерно удаленных друг от друга, являет собой геометрическую прогрессию.

По законам прогрессии установлена размерность станков и инструментов по резке металла. Вообще вычисления прогрессии становят математическую основу стандартизации промышленной продукции. С ее помощью можно вычислять проценты по банковским вкладам и многое другое. 

Характеристическое свойство геометрический прогрессии с положительными членами

Для любой геометрической прогрессии с положительными членами верна следующая теорема, которая, в частности, объясняет название «геометрическая прогрессия».

Теорема. Любой член геометрической прогрессии с положительными членами

a₁, a₂, …, a_{n — 1}, a_n , a_{n + 1}, …

начиная со второго, равен среднему геометрическому соседних с ним членов.

Другими словами, при n > 2

Действительно, при n > 2

Поэтому

a_n2= a_{n — 1} • a_{n + 1}

откуда и вытекает равенство (1).

На геометрические прогрессии, содержащие отрицательные члены, эта теорема не распространяется: ведь среднее геометрическое определено только для положительных чисел.

Верна и теорема, обратная к только что доказанной.

Если каждый член числовой последовательности с положительными членами, начиная со второго, равен среднему геометрическому соседних с ним членов, то такая последовательность является геометрической прогрессией.

Убывающая прогрессия

Как было сказано выше, знаменатель убывающей бесконечно прогрессии геометрической по модулю должен быть меньше единицы, то есть |r|<1. Это означает, что он может быть как положительным, так и отрицательным.

Практический интерес представляет сумма членов прогрессии геометрической бесконечно убывающей, потому что она представляет собой некоторое конечное число.

Чтобы получить формулу для рассматриваемого случая, воспользуемся выражением для суммы, которое приведено в первом пункте статьи: Sn = a1*(rn-1)/(r-1). Если рассматривать бесконечный ряд, то есть n>∞, тогда rn>0, поскольку |r|<1. Этот факт можно проверить, если взять любое число, удовлетворяющее последнему условию, и возвести его в большую степень. В результате формула для суммы n слагаемых при n>∞ для убывающей прогрессии примет вид: S∞ = a1*/(1-r).

Приведем пример использования полученной формулы. Пусть необходимо найти бесконечную сумму для ряда 100, 50, 25, 12,5 … Как видно, первый член прогрессии геометрической убывающей бесконечно a1 равен 100, а ее знаменатель r = 0,5 (50/100 = 25/50 = 12,5/25). Подставим эти значения в формулу для бесконечной суммы, получим: S∞ = a1*/(1-r) = 100/(1-0,5) = 200.

Арифметическая и геометрическая прогрессии: в чем разница?

Арифметическая прогрессия (АП) – это последовательность, в которой разница между двумя последовательными членами постоянна. В то время как геометрическая последовательность – такая, в которой соотношение между двумя последовательными членами постоянно.

В АП члены могут быть получены путем добавления или вычитания константы к предыдущему члену, при этом в случае ГП каждый член получается путем умножения или деления константы на предыдущий член.

В АП мы добавляем или вычитаем фиксированное ненулевое число бесконечное количество раз. В этом случае последовательность выглядит так: a + d, a + 2d, a + 3d, a + 4d = 5, 8, 11, 14, 17… 

В АП изменение членов последовательности линейно. А в ГП изменение элементов последовательности экспоненциально.

Бесконечные АП расходятся, в то время как бесконечные геометрические прогрессии сходятся или расходятся, в зависимости от обстоятельств. 

Бесконечная убывающая геометрическая прогрессия — что из себя представляет

Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы \(|q| <1.\)

Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:

\(S=\frac{b_1}{1-q}.\)

Доказательством этой формулы является то, что величина \(q^n\) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.

Пример такой прогрессии:

1, \(\frac12,\) \(\frac14,\) \(\frac18\), \\(\frac1{16},…\)

Что такое геометрическая прогрессия?

Общий вид формулы геометрической прогрессии:

Первый член (a1)	Знаменатель (q)	Формула
a1	q	an = a1 * q^(n-1)

При такой формуле каждый элемент геометрической прогрессии (a_n) выражается через первый член (a₁) и знаменатель (q).

Пример прогрессии:

Первый член (a1)	Знаменатель (q)	Последовательность
2	3	2, 6, 18, 54, …

В данном примере первый член равен 2, знаменатель равен 3. Следующие элементы получаются многократным умножением предыдущего элемента на знаменатель: 2 * 3 = 6, 6 * 3 = 18, 18 * 3 = 54 и так далее.

Геометрическая прогрессия играет важную роль в математике и ее применениях. Она используется в финансовых расчетах, при моделировании роста популяции, в физике и других науках.

Разновидности

В зависимости от q и a 1, данная прогрессия разделяется на несколько видов:

Если и a 1 , и q больше единицы, то такая последовательность — возрастающая с каждым следующим элементом геометрическая прогрессия. Пример таковой представлен далее.

Пример: a 1 =3, q=2 — оба параметра больше единицы.

Тогда числовая последовательность может быть записана так:

3 6 12 24 48 …

Если |q| меньше единицы, то есть, умножение на него эквивалентно делению, то прогрессия с подобными условиями — убывающая геометрическая прогрессия. Пример таковой представлен далее.

Пример: a 1 =6, q=1/3 — a 1 больше единицы, q — меньше.

Тогда числовую последовательность можно записать таким образом:

6 2 2/3 … — любой элемент больше элемента, следующего за ним, в 3 раза.

Знакопеременная. Если q

Пример: a 1 = -3 , q = -2 — оба параметра меньше нуля.

Тогда числовую последовательность можно записать так:

3, 6, -12, 24,…

Сумма бесконечно убывающей геометрической прогрессии

До сих пор, говоря о суммах, мы всегда предполагали, что число слагаемых в этих суммах конечно (например, 2, 15, 1000 и т. д.). Но при решении некоторых задач (особенно высшей математики) приходится сталкиваться и с суммами бесконечного числа слагаемых

S = a₁ + a₂ + … + a_n + … . (1)

Что же представляют из себя такие суммы? По определению суммой бесконечного числа слагаемых a₁, a₂, …, a_n, … называется предел суммы S_n первых n чисел, когда n-> ∞:

Предел (2), конечно, может существовать, а может и не существовать. Соответственно этому говорят, что сумма (1) существует или не существует.

Как же выяснить, существует ли сумма (1) в каждом конкретном случае? Общее решение этого вопроса выходит далеко за пределы нашей программы. Однако существует один важный частный случай, который нам предстоит сейчас рассмотреть. Речь будет идти о суммировании членов бесконечно убывающей геометрической прогрессии.

Пусть a₁ , a₁q , a₁q2, …- бесконечно убывающая геометрическая прогрессия. Это означает, что |q| n членов этой прогрессии равна

Из основных теорем о пределах переменных величин получаем:

Но \(\lim_{n \rightarrow\infty}\)1 = 1, a \(\lim_{n \rightarrow\infty}q^n = 0\). Поэтому

Итак, сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрести, деленному на единицу минус знаменатель этой прогрессии.

Примеры.

1) Сумма геометрической прогрессии 1, 1/₃ , 1/₉ , 1/₂₇ , … равна

а сумма геометрической прогрессии 12; -6; 3; — 3/₂, … равна

2) Простую периодическую дробь 0,454545 … обратить в обыкновенную.

Для решения этой задачи представим данную дробь в виде бесконечной суммы:

Правая часть этого равенства представляет собой сумму бесконечно убывающей геометрической прогрессии, первый член которой равен 45/₁₀₀, а знаменатель 1/₁₀₀. Поэтому

Описанным способом может быть получено и общее правило обращения простых периодических дробей в обыкновенные:

Для обращения простой периодической дроби в обыкновенную нужно поступить следующим образом: в числителе поставить период десятичной дроби, а в знаменателе — число, состоящее из девяток, взятых столько раз, сколько знаков в периоде десятичной дроби.

3) Смешанную периодическую дробь 0,58333 …. обратить в обыкновенную.

Представим данную дробь в виде бесконечной суммы:

В правой части этого равенства все слагаемые, начиная с 3/₁₀₀₀, образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен 3/₁₀₀₀, а знаменатель 1/₁₀. Поэтому

Описанным способом может быть получено и общее правило обращения смешанных периодических дробей в обыкновенные, но оно громоздкое. Гораздо полезнее знать, что любую смешанную периодическую дробь можно представить в виде суммы бесконечно убывающей геометрической прогрессии и некоторого числа. А формулу

для суммы бесконечно убывающей геометрической прогрессии нужно запомнить.

Что такое геометрическая прогрессия

Геометрическая прогрессия (ГП) — это последовательность чисел, в которой каждое следующее число получается путем умножения предыдущего числа на постоянное число, называемое знаменателем прогрессии (q). Формула общего члена геометрической прогрессии имеет вид:

aₙ = a₁ * q^(n-1),

где aₙ — n-й член прогрессии, a₁ — первый член прогрессии, q — знаменатель прогрессии, n — номер члена последовательности.

Основные свойства геометрической прогрессии

• 1. Знаменатель геометрической прогрессии (q): Знаменатель прогрессии (q) является постоянным числом, на которое умножается каждый член последовательности, чтобы получить следующий член. Знаменатель может быть как положительным, так и отрицательным числом. Если |q| < 1, то последовательность сходится к нулю при увеличении номера члена, а если |q| > 1, то последовательность расходится. Если q = 1, то все члены последовательности будут равными.
• 2. Общий член геометрической прогрессии (aₙ): Общий член геометрической прогрессии (aₙ) определяется формулой aₙ = a₁ * q^(n-1), где a₁ — первый член прогрессии, q — знаменатель прогрессии, n — номер члена последовательности. Эта формула позволяет нам находить любой член прогрессии, зная значения первого члена и знаменателя.
• 3. Сумма членов геометрической прогрессии (Sₙ): Сумма первых n членов геометрической прогрессии (Sₙ) может быть вычислена по формуле Sₙ = a₁ * (1 — q^n) / (1 — q), где a₁ — первый член прогрессии, q — знаменатель прогрессии, n — количество членов, для которых мы хотим найти сумму. Эта формула позволяет нам вычислять сумму членов прогрессии.

Виды геометрической прогрессии

• 1. Убывающая геометрическая прогрессия: В убывающей геометрической прогрессии (q < 0) каждый следующий член будет меньше предыдущего. Например, последовательность (8, -4, 2, -1, 0.5) является убывающей геометрической прогрессией с знаменателем q = -0.5.
• 2. Возрастающая геометрическая прогрессия: В возрастающей геометрической прогрессии (q > 0) каждый следующий член будет больше предыдущего. Например, последовательность (1, 3, 9, 27, 81) является возрастающей геометрической прогрессией с знаменателем q = 3.
• 3. Константная геометрическая прогрессия: В константной геометрической прогрессии (q = 1) все члены прогрессии будут равными. Например, последовательность (4, 4, 4, 4, 4) является константной геометрической прогрессией.

Примеры решения задач

Пример 1: Задача о сумме первых n членов геометрической прогрессии

Найдите сумму первых 5 членов геометрической прогрессии, если первый член равен 2, а знаменатель равен 3.

Решение:

Дано: a₁ = 2 (первый член), q = 3 (знаменатель), n = 5 (количество членов для которых нужно найти сумму).

Используем формулу для суммы первых n членов геометрической прогрессии:

Sₙ = a₁ * (1 — qⁿ) / (1 — q).

Подставляем значения:

S₅ = 2 * (1 — 3⁵) / (1 — 3).

Расчитываем значение:

S₅ = 2 * (1 — 243) / (-2).S₅ = 2 * (-242) / (-2).S₅ = -484.

Таким образом, сумма первых 5 членов геометрической прогрессии равна -484.

Пример 2: Задача о нахождении n-го члена геометрической прогрессии

Найдите 8-й член геометрической прогрессии, если первый член равен 1, а знаменатель равен 2.

Решение:

Дано: a₁ = 1 (первый член), q = 2 (знаменатель), n = 8 (номер члена, который нужно найти).

Используем формулу для общего члена геометрической прогрессии:

aₙ = a₁ * q^(n-1).

Подставляем значения:

a₈ = 1 * 2^(8-1).

Расчитываем значение:

a₈ = 1 * 2^7.a₈ = 1 * 128.a₈ = 128.

Таким образом, 8-й член геометрической прогрессии равен 128.

Пример 3: Задача о поиске знаменателя геометрической прогрессии
В геометрической прогрессии первый член равен 4, а сумма первых 5 членов равна 124. Найдите знаменатель прогрессии.

Решение:

Дано: a₁ = 4 (первый член), S₅ = 124 (сумма первых 5 членов).

Используем формулу для суммы первых n членов геометрической прогрессии:

S₅ = a₁ * (1 — qⁿ) / (1 — q).

Подставляем значения:

124 = 4 * (1 — q⁵) / (1 — q).

Раскрываем скобки и упрощаем уравнение:

124 = 4 — 4q⁵ / (1 — q).

Умножаем обе части уравнения на (1 — q) и получаем:

124 — 124q = 4 — 4q⁵.

Раскрываем степень:

124 — 124q = 4 — 4q * 4 * 4 * 4 * 4.124 — 124q = 4 — 256q.

Объединяем подобные члены:

-124q + 256q = 4 — 124.132q = -120.q = -120 / 132.q = -10 / 11.

Таким образом, знаменатель геометрической прогрессии равен -10 / 11.

Сумма бесконечно убывающей геометрической прогрессии

Суммой членов бесконечно убывающей геометрической прогрессиисо знаменателем называется число .

Это определение объясняется тем, что с увеличением число все меньше отличается от суммы первых членов этой прогрессии. Действительно,

.

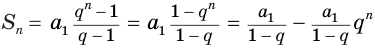Поскольку , то с увеличением приближается к нулю, а значит, приближается к нулю и вычитаемое . Поэтому сумма приближается к .

Пример №1

Найдем значение суммы

.

Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой
и . Поэтому

Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:

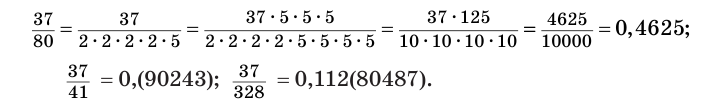
Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.

Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.

В дальнейшем мы будем пользоваться записью вида . Она обозначает десятичную дробь, целая часть которой записана с помощью цифр , а дробная — с помощью цифр .

Теорема 7.

Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.

Доказательство:

Пусть — периодическая десятичная дробь, где — цифры периода. Тогда число
можно представить бесконечной суммой:

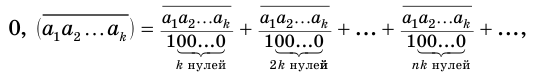
в которой каждое слагаемое получается из предыдущего умножением на . Это означает, что бесконечную периодическую дробь можно рассматривать как сумму
членов бесконечно убывающей геометрической прогрессии с первым

членом
и знаменателем . Поэтому

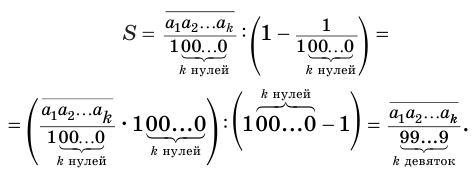
Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.

Пример №2

Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:

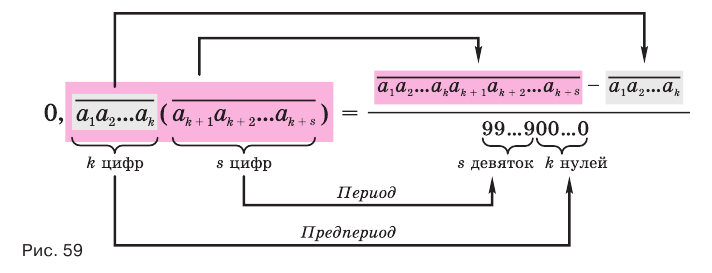
Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.

Доказательство:

Пусть — периодическая десятичная дробь, где — цифры предпериода, — цифры периода. Тогда число можно представить суммой

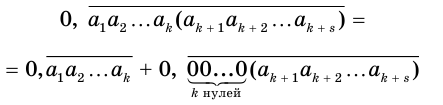
или, с учетом теоремы 7, суммой

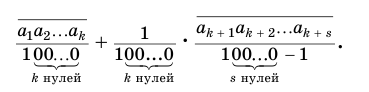
Преобразуем полученное выражение:

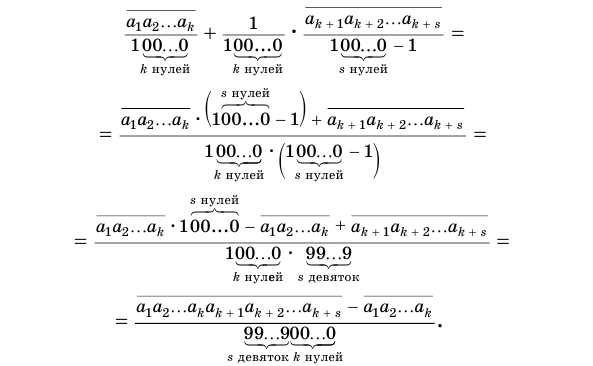
Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом, который отражен на схеме, представленной на рисунке 59.

Сумма первых членов арифметической прогрессии

Интересный случай произошел с Карлом Гауссом, известным математиком, ещё в третьем классе. Учитель предложил ученикам найти сумму первых 100 натуральных чисел. Однако Гаусс почти сразу сказал ответ: 5050. Как он смог так быстро сложить 100 чисел?

Он догадался, что в сумме

1 + 2 + 3 + 4…+ 99 + 100

можно поменять местами слагаемые, чтобы после первого было записано последнее слагаемое, после второго – предпоследнее и т.д. В итоге получится сумма

(1 + 100) + (2 + 99) + (3 + 98) + … (50 + 51)

В каждой скобке сумма слагаемых равна 101:

1 + 100 = 101

2 + 99 = 101

3 + 98 = 101

Всего же есть 50 таких скобок, каждая из которых равна 101, поэтому общая сумма равна 101•50 = 5050.

Так как натуральные числа образуют ариф. прог-сию, в которой b₁ = 1 и d = 1, то Гаусс, по сути, нашел сумму первых 100 членов ариф. прог-сии. Иногда ее просто называют суммой арифметической прогрессии. Обозначают эту сумму буквой S_n, где n – это количество первых членов прог-сии, которые надо сложить. Вычислить S_n можно так:

S₁ = b₁

S₂ = b₁ + b₂ = S₁ + b₂

S₃ = b₁ + b₂ + b₃ = S₂ + b₃

…

S_n = b₁ + b₂ + b₃ + … + b_n = S_n–1 + b_n

Однако такой способ требует, очевидно, большого объема вычислений. Есть и более короткий способ – воспользоваться формулой

Докажем ее справедливость, используя индукцию. Подставим в формулу n=1 и убедимся, что в этом случае она работает:

Получили верную формулу S₁ = b₁

Базис индукции доказан. Далее покажем, что если формула справедлива при n = k, то она истинна и при n = k + 1. То есть надо доказать, что

Действительно, сумма (k + 1) слагаемых равна

Слагаемые справа можно представить так:

S_k = (2b₁ + d(k – 1))•k/2 (потому что мы предполагаем, что формула справедлива для n = k)

b_k+1= b₁ + (k + 1 – 1)•d = b₁ + kd (формула n-ого члена ариф. прог-сии)

Тогда можно записать:

Докажем, что выр-ния (1) и (2) тождественно равны друг другу:

Умножим на двойку обе части равенства:

Раскроем скобки:

И справа, и слева стоят одинаковые выр-ния, поэтому равенство является тождеством. Значит, используемая нами формула справедлива.

Посмотрим, как использовать эту формулу на практике. Начнем с задачи, решенной в третьем классе Гауссом. Послед-ть натуральных чисел – это ариф. прог-сия, в котором 1-ый член b₁ = 1, разность d = 1. Гауссу надо было найти сумму первых 100 чисел, поэтому n = 100. Подставляем в формулу эти данные и получаем:

Получили тот же результат, что и Гаусс.

Пример. Сложите первую тысячу нечетных натуральных чисел.

Решение. Послед-ть нечетных натуральных чисел выглядит так:

1, 3, 5, 7…

Очевидно, что это ариф. прог-сия, ведь каждое следующее число получается добавлением двойки к предыдущему. У этой прог-сии b₁ = 1, d = 2. Тогда сумма 1000 чисел будет равна:

Ответ: 1000000.

Пример. Сложите все трехзначные натуральные числа.

Решение. Нам надо сложить числа от 100 до 999. Здесь можно предложить два алгоритма решения.

Первый способ. Сложим числа от 1 до 99:

Далее сложим числа от 1 до 999:

Для того, чтобы найти сумму от 100 до 999, вычтем из S₉₉₉ сумму S₉₉:

Второй способ. Трехзначные нат. числа образуют ариф. прог-сию:

100, 101, 102, 103…

у которой b₁ = 100, а разность d = 1. Сколько всего есть трехзначных чисел? Всего есть 999 чисел от 1 до 999, для записи которых хватает 3 цифр. Однако для первых 99 из них достаточно двух или даже одной цифры. Поэтому трехзначных чисел всего 999 – 99 = 900.

По этой причине примем n = 900. Далее подставим параметры прогрессии в формулу и получим:

Ответ: 494550

Пример. Задана ариф. прог-сия, у которой b₁ = 125, d = – 19:

125, 106, 87, 68, 49…

Чему равна сумма первых 50-ти ее членов? Какова сумма вторых 50-ти членов послед-ти?

Решение. Для нахождения суммы первых 50-ти членов подставим в формулу условия задачи:

Для ответа на второй вопрос задачи предварительно вычислим сумму 100 первых чисел:

Сумма вторых 50-ти чисел равна разнице S₁₀₀– S₅₀:

Ответ: – 64525

Пример. Решите уравнение, зная, что слева записана арифм. прог-сия:

2 + 8 + 14 + 20 + … + х = 184

Решение. Ясно, что в данной прог-сии b₁ = 2. Разность прог-сии можно определить, просто вычтя из второго члена прог-сии первый:

d = 8 — 2 = 6

Слева записана сумма первых n слагаемых (n нам неизвестно). Заменим это выражение формулой:

По условию эта сумма равна 184. Тогда можно записать равенство:

Имеем уравнение, из которого можно найти n. Сначала умножим обе части на 2:

По таблице квадратов можно узнать, что квадратный корень из 8836 равен 94, ведь 942 = 8836. Тогда корни квадр. ур-ния будут равны:

Первый корень – лишний, ведь n может быть только нат. числом. Поэтому n = 8.

Если слева в исходном ур-нии

стоит сумма n = 8 членов ариф. прог-сии, то х – это восьмой ее член. Найти его можно, используя формулу:

Подставим х в ур-ние и убедимся, что мы не ошиблись:

Проверка подтвердила правильность решения.

Примеры бесконечно убывающих геометрических прогрессий

Приведем примеры бесконечно убывающих геометрических прогрессий.

Пример №1

Последовательность

является бесконечно убывающей геометрической прогрессией спервым членом и знаменателем

Пример №2

Последовательность

является бесконечно убывающей геометрической прогрессией с первым членом и знаменателем
(здесь ). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).

Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением
этот модуль становится меньше любого заданного положительного числа.

Например, если мы зададим число 0,01, то

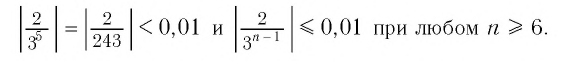
Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).

И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.

Например, если мы зададим число 0,001, то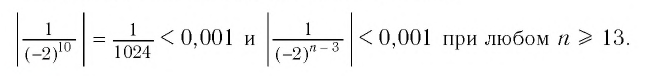
Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии
чем больше номер п члена прогрессии тем меньше и с увеличением этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:стремится к нулю при стремящемся к бесконечности.

Заметим, что если стремится к нулю при стремящемся к бесконечности.

Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членоми знаменателем

Запишем формулу суммы первых членов этой прогрессии и преобразуем это выражение:
Обозначим

Тогда получим

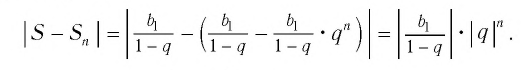
Так как стремится к нулю при стремящемся к бесконечности. Значит,
стремится к нулю при , стремящемся к бесконечности, т. е. чем больше число (чем больше слагаемых в сумме ), темменьше разница между и
Поэтому число называют суммой бесконечно убывающей геометрической прогрессии.

Пример №3

Найти сумму бесконечно убывающей геометрической прогрессии:

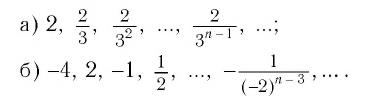
Решение:

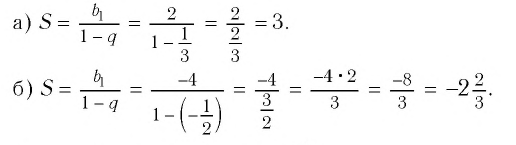
Ответ: