Скалярное произведение векторов

13 Координаты вектора, радиус-вектора и точки

Координаты
вектора — это координаты конца вектора, если начало вектора поместить
в начало координат.

Радиус-вектор
— это вектор, проведенный из начала координат к данной точке,
координаты радиус-вектора и точки равны.

Если
вектор

задан точками M₁(x₁;
y₁; z₁)
и M₂(x₂;
y₂; z₂),
то каждая из его координат равна разности соответствующих координат
конца и начала вектора

=
(x₂
— x₁;
y₂
— y₁;
z₂
— z₁)
= (x_a; y_a; z_a)

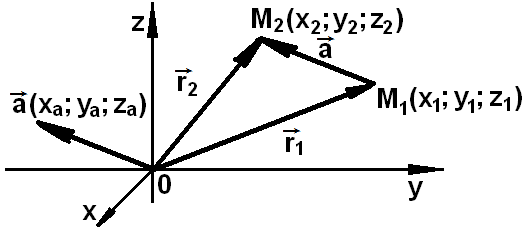
Для
коллинеарных векторов

=
(x₁; y₁;
z₁) и

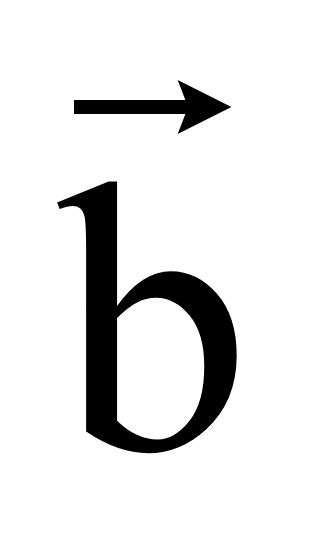
= (x₂; y₂;
z₂), если

≠ 0, то существует единственное число k,
позволяющее выразить вектор

через

:

=
k

Тогда
координаты вектора

выражаются через координаты вектора

=
(kx₁; ky₁;
kz₁) = (x₂;
y₂;
z₂).

Отношение
соответствующих координат коллинеарных векторов

и

равно единственному числу k

Если
отношение соответствующих координат векторов

и

равно единственному числу k, то
эти векторы коллинеарны. В противном случае векторы

и

неколлинеарны.

Кратчайшее расстояние от точки до плоскости

Итак есть плоскость задання с помощью точки (p0) в трехмерном пространстве и вектора нормали (n) плоскости. И есть точка (p1) заданная в виде координаты. 

Кратчайшим расстоянием от точки до плоскости будет перпендикуляр опущенный из этой точки на эту плоскость. Если что — вектор этого перпендикуляра мы уже знаем — это наша нормаль. 

А вот как найти расстояние? 

Проведем вектор из точки задающей плоскость к искомой точке — 

v =  (X = p1.x-p0.x, Y=p1.y-p0.y, Z=p1.z-p0.z) = (X,Y,Z)

Итак есть вектор, есть нормаль. И… а собственно и все — ответом будет скаляр между этим вектором и нормалью. 

dot = n.X*v.X + n.Y*v.Y+n.Z*v.Z 

Потому что нормаль это перпендикуляр. Гипотенуза прямоугольника найденный вектор. А Скаляр этой гипотенузы и этого вектора  даст длинну катета от искомой точки до плоскости. 

Определение смешанного произведения векторов

Определение: Смешанным произведением векторов называется число  – скалярное произведение a  на векторное произведение
Смешанное произведение обозначается так:

Пусть в некоторой пдск
Обозначим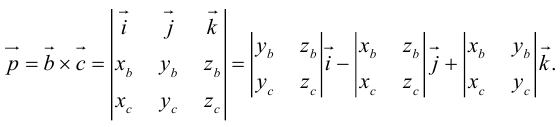      
Тогда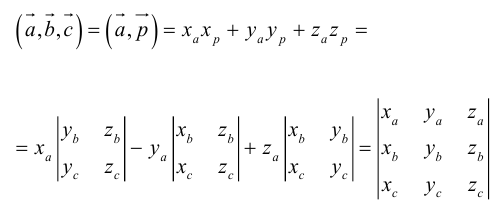   
по 7 свойству определителей. 
Таким образом,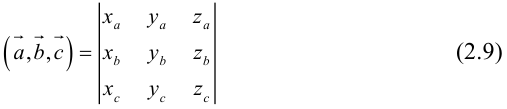                              
По  определению  скалярного  произведения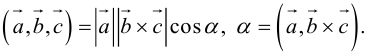 
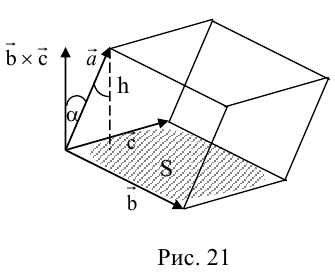
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)   – площадь параллелограмма,    – высота параллелепипеда,   – объем параллелепипеда.  

Геометрический  смысл  смешанного  произведения:  модуль  смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях,  при  этом  –  правая  тройка,  и  – левая тройка. 
 

Свойства смешанного произведения

1. Необходимым и достаточным условием компланарности трех векторов является  равенство  нулю  их  смешанного  произведения:    компланарны  
 

Доказательство:   а) компланарны
Если компланарны, то на них нельзя построить параллелепипед, а потому
б)компланарны.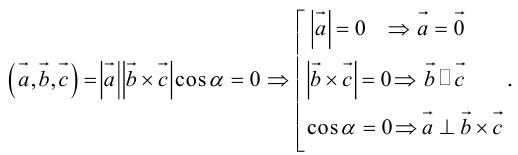   
Во всех трех случаях   компланарны: в частности,  если  параллелен плоскости векторов  , что означает их компланарность. 

2.  Круговая  перестановка  сомножителей  в  смешанном  произведении  не изменяет  его  величины.  Перестановка  соседних  сомножителей  изменяет  его знак, не изменяя абсолютной величины: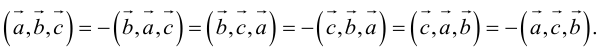  

Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.  

3. В смешанном произведении векторное и скалярное произведения можно менять местами:
 

Доказательство:  из свойства 2 смешанного произведения и свойства 1 скалярного получим:

4.  Смешанное произведение линейно по каждому из трех сомножителей.  – линейность по первому сомножителю. 

Доказательство следует из формулы (2.9) и свойств определителей. 

Пример №14

Найти  объем  тетраэдра,  построенного  на  векторах   , и его высоту, перпендикулярную плоскости векторов . 
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому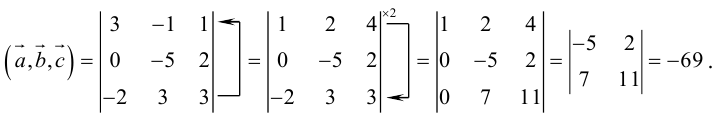
Отсюда (заметим, что – левая тройка, так как смешанное произведение отрицательно). 
Чтобы найти высоту, воспользуемся формулой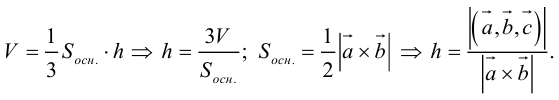    
По формуле (2.7)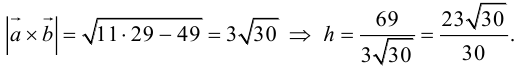

Лекции по предметам:

1. Математика
2. Алгебра
3. Линейная алгебра
4. Геометрия
5. Аналитическая геометрия
6. Высшая математика
7. Дискретная математика
8. Математический анализ
9. Теория вероятностей
10. Математическая статистика
11. Математическая логика

Скалярное произведение двух векторов простыми словами

Пусть теперь вектор V1 = (10, 5) , а вектор V2 = (10,10)

dot = V1.X*V2.X + V1.Y*V2.Y = 10*10 + 5*10 = 100+50=150

Вектора вроде не большие, а их скалярное произведение получилось здоровенным. Как так то? Что нам дает эта цифра? Что она вообще значит? 

Это не похоже на векторное сложение и произведение. Это просто огромная цифра. Но каково её геометрическое значение?

Единичный вектор с единичным — дают косинус ( он же — прилежащий катет единичного вектора). 

Единичный вектор с вектором больше или меньше единичного — дает длинну катета прямоугольного треугольника образованного этими двумя векторами. Иначе говоря — мы косинус угла между векторами умножили на длинну вектора, который не равен единице, и получили длинну катета. Это как на анимации выше — там два единичных вектора, и поэтому косинус умножить на единицу — всё равно косинус , а вот если один вектору у нас был равен пяти единичным векторам а другой единице — то единицу отбрасываем, а косинус умножаем на 5. Но прелесть в том что нам не надо это делать, достаточно посчитать скалярное произведение,  и всё, значение катета у нас в кармане. Можем потом из этого значения найти и сам косинус поделив катет на длинну вектора.  

Зная это теперь мы можем объяснить откуда в примере выше взялось такое несуразно огромное число. Неединичный вектор на неединичный вектор дает нам катет, но длинна его умножена на длинну вектора.  Иначе говоря у нас есть V1 который равен 5 единичным векторам, и V2 который равен десяти единичным векторам. Так вот наше произведение нам даст такую штуку как если мы умножили два единичных вектора и получив косинус угла между ними — умножили его на длинну первого вектора, получив его катет, а потом этом катет умножили на длинну второго вектора. 

Причем, так как это умножение и сложение, можно эти шаги переставлять местами, результат будет одинаков.

А главное — нам не нужно делать эти шаги. Достаточно посчитать скалярное произведение.

Векторное произведение векторов

Так иногда бывает, что для полного счастья математикам нужно что-то еще, и если скалярное произведение еще может быть знакомо со школы, то векторное произведение чаще всего изучают в ВУЗе на курсах вышмата.

Обрадую всех вас — если все, что происходило до этого работало и в двухмерном и в трехмерном пространстве, то векторное произведение векторов подразумевает работу ТОЛЬКО с трехмерным пространством. (Стало проще, да ведь?)

В данном произведении участвуют также 2 вектора. Отличие от скалярного произведения тех же двух векторов будет в том, что в результате векторного произведения получается ВЕКТОР, а не число.

Формальное определение:
 

Векторным произведением  ā x b̅  неколлинеарных векторов  ā и b̅, взятых в определенном порядке, называется ВЕКТОР ā x b̅ , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ā x b̅  ортогонален векторам  ā и b̅, и направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию.

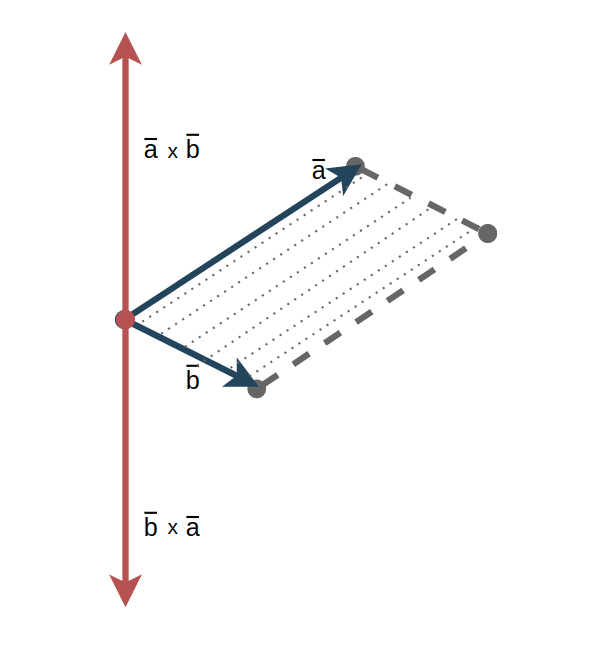
Это определение сложное и требует некоторых комментариев:

1. 

Векторы ā и b̅ по определению должны быть неколлинеарны. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Таким образом такие векторы могут называться параллельными, но так называть вектора просто не принято — их называют коллинеарными. Касаемо ситуации с векторным произведением — векторы должны быть, наоборот, непараллельными.

2.

 Важен порядок векторов. От этого зависит направление результата.

3.

Длина результирующего вектора равна площади заштрихованного параллелограмма. 

4.

Результирующий вектор ортогонален векторам  ā и b̅, т.е.  ā ┴   и  b ┴ 

5.

Результирующий вектор  направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию. 

Мысленно совместите указательный палец с вектором ā и средний палец с вектором b̅. Безымянный палец и мизинец прижмите к ладони. В результате большой палец – результирующий вектор будет смотреть вверх. Это правоориентированный базис.

Указательный палец левой руки с тем же вектором  ā, а средний – с вектором b̅. При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис.

Эти базисы не являются чем-то абстрактным. Примером может служить изображение и его отражение в зеркале. Самое обычное зеркало меняет ориентацию пространства, а изображение и зеркальное отражение этого отображения невозможно просто наложить друг на друга (попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются).

Что же будет, если вектора  ā и b̅ будут коллинеарны (т.е. параллельны, говоря на простом языке) — все просто, параллелаграм, который образуется этими векторами “складывается” в плоскую прямую, а площадь такой прямой равна нулю, из-за чего и результирующий вектор равен нулевому.  

Свойства[править]

Переместительное свойство:

r1⋅r2=r2⋅r1.{\displaystyle \mathbf {r} _{1}\cdot \mathbf {r} _{2}=\mathbf {r} _{2}\cdot \mathbf {r} _{1}.}

Два свойства линейности:

• (r1+r2)⋅r3=r1⋅r3+r2⋅r3,r1⋅(r2+r3)=r1⋅r2+r1⋅r3;{\displaystyle (\mathbf {r} _{1}+\mathbf {r} _{2})\cdot \mathbf {r} _{3}=\mathbf {r} _{1}\cdot \mathbf {r} _{3}+\mathbf {r} _{2}\cdot \mathbf {r} _{3},\qquad \mathbf {r} _{1}\cdot (\mathbf {r} _{2}+\mathbf {r} _{3})=\mathbf {r} _{1}\cdot \mathbf {r} _{2}+\mathbf {r} _{1}\cdot \mathbf {r} _{3};}
• (a1r1)⋅(a2r2)=a1a2(r1⋅r2).{\displaystyle (a_{1}\mathbf {r} _{1})\cdot (a_{2}\mathbf {r} _{2})=a_{1}a_{2}(\mathbf {r} _{1}\cdot \mathbf {r} _{2}).}

Скалярный квадрат:

(a1, …,an)⋅(a1, …,an)=|(a1, …,an)|2=a12+…+an2.{\displaystyle (a_{1},\ …,a_{n})\cdot (a_{1},\ …,a_{n})=|(a_{1},\ …,a_{n})|^{2}=a_{1}^{2}\,+\,…+\,a_{n}^{2}.}

Умножение на нулевой вектор:

r⋅=⋅r=.{\displaystyle \mathbf {r\cdot 0} =\mathbf {0\cdot r} =\mathbf {0} .}

Распределительное свойство

Отдельного внимания, пожалуй, заслуживает распределительное свойство, или дистрибутивность, скалярного умножения относительно сложения. Дело в том, что доказательство — да и вообще само реальное понимание причины этого свойства возникает именно при использовании определения через проекцию, так как в таком случае теорема оказывается очень очевидной:

(r1+r2)⋅r3=(projr3(r1+r2))r3=(projr3r1+projr3r2)r3=r1⋅r3+r2⋅r3,{\displaystyle (\mathbf {r} _{1}+\mathbf {r} _{2})\cdot \mathbf {r} _{3}={\big (}{\text{proj}}_{\mathbf {r} _{3}}(\mathbf {r} _{1}+\mathbf {r} _{2}){\big )}r_{3}=({\text{proj}}_{\mathbf {r} _{3}}\mathbf {r} _{1}+{\text{proj}}_{\mathbf {r} _{3}}\mathbf {r} _{2})r_{3}=\mathbf {r} _{1}\cdot \mathbf {r} _{3}+\mathbf {r} _{2}\cdot \mathbf {r} _{3},}

если конец первого слагаемого внутри скобки совместить с началом второго слагаемого.

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

A=(F→,MN→).

Пример 8

Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.

Решение

Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.

Ответ: A=1522.

Пример 9

Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.

Решение

При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).

По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.

По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).

Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:

MN→=32+(-10)2+72=158.

Ответ: 158.

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Свойства скалярного произведения векторов

Алгебраические свойства

1.   (переместительное свойство: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).

2.   (сочетательное относительно числового множителя свойство: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).

3.   (распределительное относительно суммы векторов свойство: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).

4. (скалярный квадрат вектора больше нуля),
если — ненулевой вектор, и ,
если — нулевой вектор.

Геометрические свойства

В определениях изучаемой операции мы уже касались понятия угла между двумя векторами.
Пора уточнить это понятие.

На рисунке выше видны два вектора, которые приведены к общему началу

И первое, на что нужно
обратить внимание: между этими векторами существуют два угла —
и. Какой из этих углов фигурирует в определениях и свойствах
скалярного произведения векторов? Сумма рассмотренных углов равна и поэтому
косинусы этих углов равны

В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит ,
то есть 180 градусов. На рисунке этот угол обозначен как .

1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или ), если скалярное произведение этих векторов равно нулю:

.

Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.

2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше ) тогда и только тогда, когда их скалярное произведение
положительно.

3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше ) тогда и только тогда, когда их скалярное произведение отрицательно.

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 3. В координатах даны векторы:

.

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Решение. Вычислять будем путём сложения произведений соответствующих координат.

.

Получили отрицательное число, поэтому векторы образуют тупой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили нуль, поэтому векторы образуют прямой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

Пример 4. Даны длины двух векторов и угол между ними:

.

Определить, при каком значении числа
векторы и
ортогональны (перпендикулярны).

Решение. Перемножим векторы по правилу умножения многочленов:

.

Теперь вычислим каждое слагаемое:

.

Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:

Ответ: мы получили значение ,
при котором векторы ортогональны.

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 5. Доказать, что вектор
ортогонален (перпендикулярен) вектору

Решение. Чтобы проверить ортогональность, перемножим векторы
и
как многочлены, подставляя
вместо его выражение, данное
в условии задачи:

.

Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член
второго и полученные произведения сложить:

.

В полученном результате дробь за счёт
сокращается. Получается следующий результат:

.

Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.

Решить задачу самостоятельно, а затем посмотреть решение

Пример 6. Даны длины векторов
и
, a
угол между этими векторами равен . Определить, при каком значении
векторы и
взаимно перпендикулярны.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

Равносильность определений[править]

Если между определениями через проекцию и через косинус равносильность довольно ясна, то их равносильность по отношению к координатному определению не очень очевидна. Для того, чтобы это «прочувстовать», можно использовать доказательство с использованием дистрибутивности (которую, в свою очередь, мы доказали с помощью определения через те самые проекции):

(a1i1+…+anin)⋅(b1i1+…+bnin)=a1i1⋅(b1i1+…+bnin)++a2i2⋅(b1i1+…+bnin)++…++anin⋅(b1i1+…+bnin)==a1b1++…++anbn.{\displaystyle {\begin{aligned}(a_{1}\mathbf {i} _{1}\,+\,…+\,a_{n}\mathbf {i} _{n})\cdot (b_{1}\mathbf {i} _{1}\,+\,…+\,b_{n}\mathbf {i} _{n})&=a_{1}\mathbf {i} _{1}\cdot (b_{1}\mathbf {i} _{1}\,+\,…+\,b_{n}\mathbf {i} _{n})\,+\\&+a_{2}\mathbf {i} _{2}\cdot (b_{1}\mathbf {i} _{1}\,+\,…+\,b_{n}\mathbf {i} _{n})\,+\\&+\,…+\\&+a_{n}\mathbf {i} _{n}\cdot (b_{1}\mathbf {i} _{1}\,+\,…+\,b_{n}\mathbf {i} _{n})=\\&=a_{1}b_{1}+\\&+\,…+\\&\,+a_{n}b_{n}.\end{aligned}}}

21 Условие перпендикулярности векторов

Если
ненулевые векторы

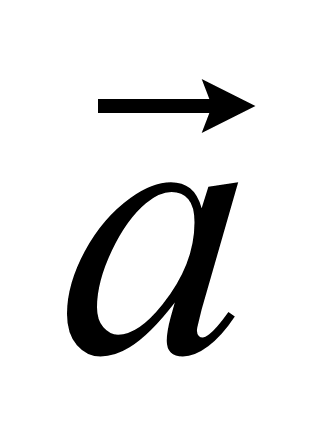
= (x₁; y₁;
z₁) и

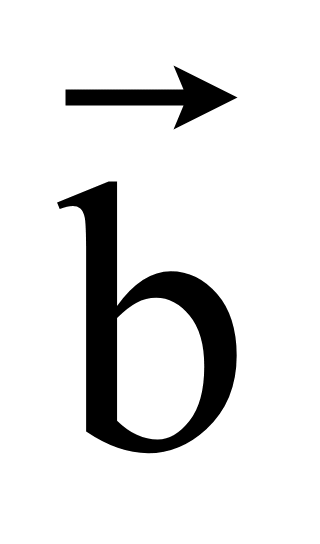
= (x₂; y₂;
z₂) перпендикулярны, то их
скалярное произведение равно нулю

=
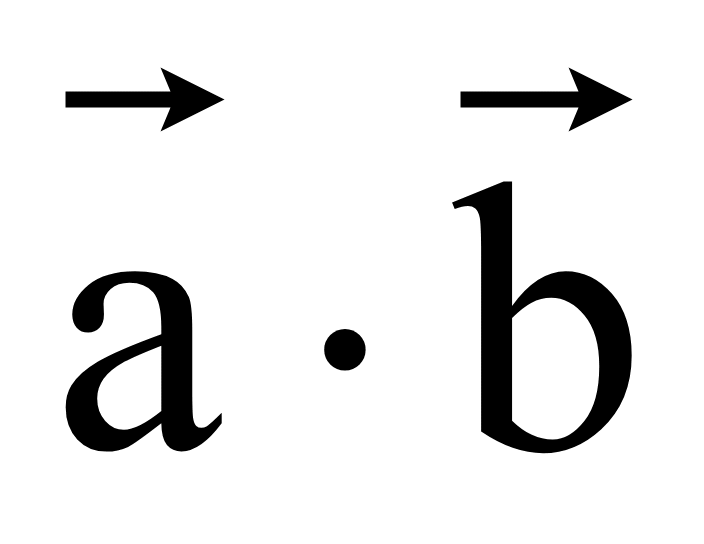0,

=
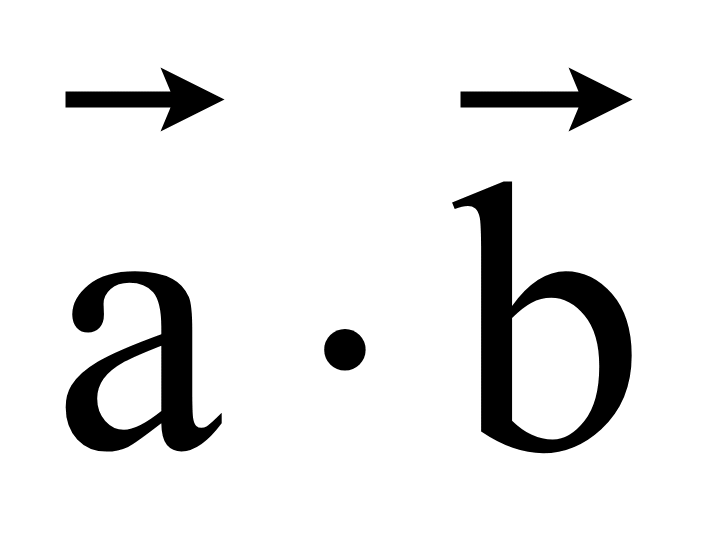x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Если
задан один ненулевой вектор

= (x₁; y₁;
z₁), то координаты
перпендикулярного (нормального) ему ненулевого
вектора

= (x₂; y₂;
z₂) должны удовлетворять
равенству

x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Таких
векторов

бесконечное множество.

Если
на плоскости задан один ненулевой вектор

= (x₁; y₁),
то координаты перпендикулярного (нормального) ему вектора

= (x₂; y₂)
должны удовлетворять равенству

x₁x₂
+ y₁y₂
= 0.

Отсюда
можно выразить произведение координат y

y₁y₂
= — x₁x₂.

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора

= (x₂; y₂)
и из условия перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

выразить
вторую координату вектора

.

Например,
если подставить произвольную координату x₂,то из равенства

y₁y₂
= — x₁x₂

выражается
вторая координата вектора

Если
произвольно придать x₂ = y₁,
то вторая координата вектора

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то перпендикулярный (нормальный) ему вектор

= (y₁; -x₁).

Если
одна из координат ненулевого вектора

равна нулю, то у перпендикулярного ему ненулевого вектора

такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если

= (; y₁),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор

= (x₂;
0) лежит на оси Ox.

Определим
второй вектор, перпендикулярный вектору

= (x₁; y₁),
но противоположный вектору

= (y₁; -x₁),
то есть вектор —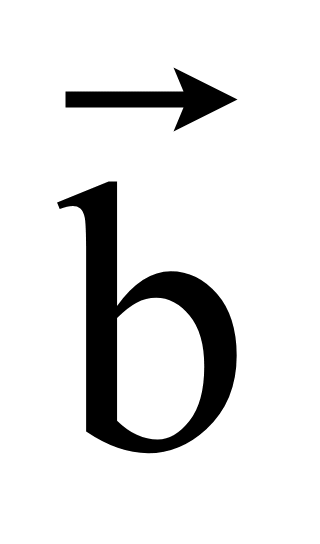
.
Тогда достаточно поменять знаки координат вектора

—

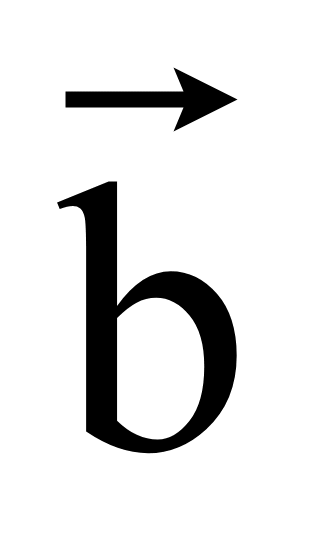
= -1·

= (-1·y₁;
-1·(-x₁))=
(-y₁; x₁).

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Для
получения координат ненулевых векторов, перпендикулярных заданному
ненулевому вектору на плоскости, достаточно поменять местами
координаты заданного вектора и поменять знак одной из координат.

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Подставляем
координаты вектора

= (3; -5)

₁
= (-5; -3),

₂
= (-(-5); 3) = (5; 3).

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·(-5)
+ (-5)·(-3) = -15 + 15 = 0

верно!

3·5
+ (-5)·3 = 15 — 15 = 0

верно!

Ответ:
₁
= (-5; -3),
₂
= (5; 3).

Если
присвоить x₂ = 1, подставить

x₁
+ y₁y₂
= 0.

y₁y₂
= -x₁

Получим
координату y₂ вектора,
перпендикулярного вектору

= (x₁; y₁)

Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору

= (x₁; y₁)

Для
получения второго вектора, перпендикулярного вектору

= (x₁; y₁),
но противоположно направленного вектору

.
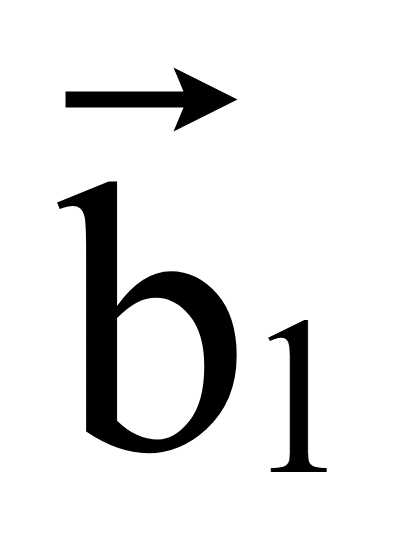
Пусть

Тогда
достаточно поменять знаки координат вектора

.

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

Координаты
одного вектора

Координаты
второго вектора

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·1
+ (-5)·0,6 = 3 — 3 = 0

верно!

3·(-1)
+ (-5)·(-0,6) = -3 + 3 = 0

верно!

Ответ:

и

.

Если
присвоить x₂ = — x₁,
подставить

x₁(-x₁)
+ y₁y₂
= 0.

-x₁2
+ y₁y₂
= 0.

y₁y₂
= x₁2

Получим
координату вектора, перпендикулярного вектору

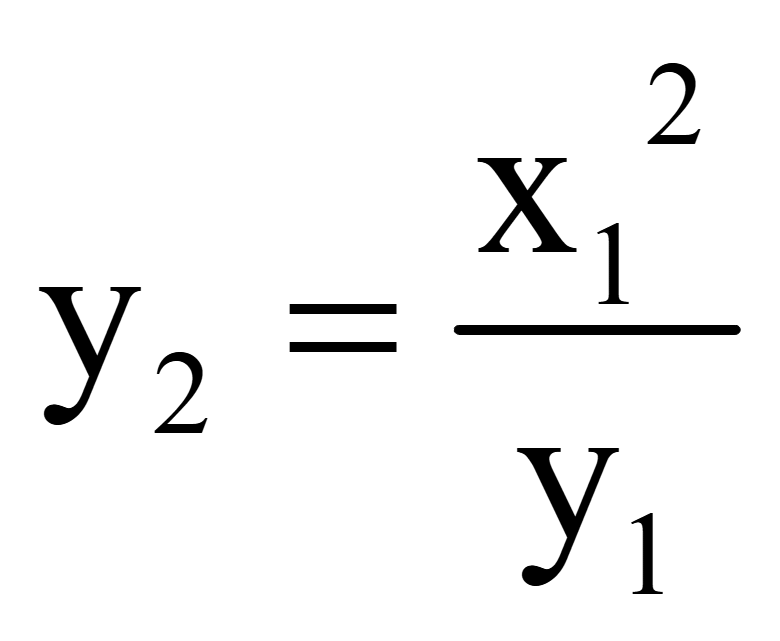
Если
присвоить x₂ = x₁,
подставить

x₁x₁
+ y₁y₂
= 0.

x₁2
+ y₁y₂
= 0.

y₁y₂
= -x₁2

Получим
координату y второго вектора,
перпендикулярного вектору

Координаты
одного вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

12 Координаты вектора в пространстве

В
пространстве зададим прямоугольную систему координат Oxyz.
От начала координат в положительных направлениях осей Ox,
Oy, Oz проведем
соответствующие единичные векторы

,

,

,
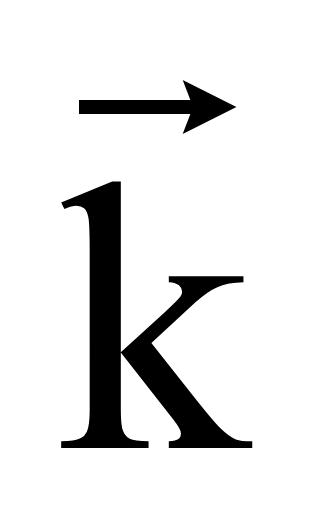
которые называются координатными векторами, неколлинеарны и
некомпланарны. Поэтому любой вектор

,
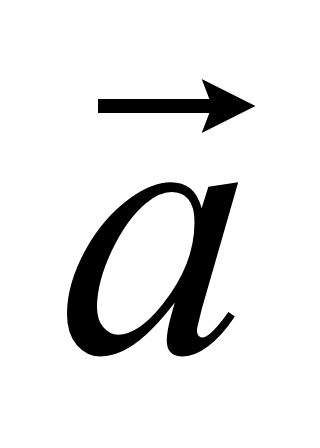
проведенный из начала координат, разлагается по трем заданным
некомпланарным координатным векторам

,

и

с единственными коэффициентами разложения x,
y, z:

=
x

+ y
+
z
.

Коэффициенты
разложения x, y,
z являются координатами вектора

,
проведенного из начала заданной прямоугольной системы координат,
которые записываются в скобках

(x;
y; z). Координаты
конца такого вектора являются и координатами вектора. Нулевой вектор
имеет координаты равные нулю

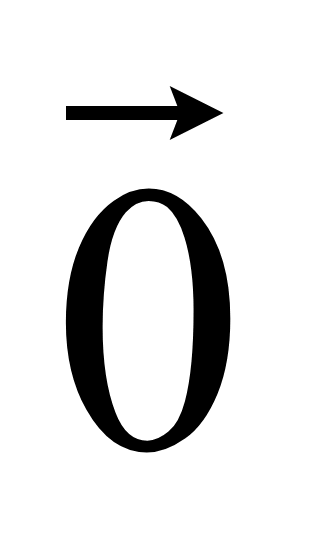
(0;
0; 0). У равных векторов соответствующие координаты равны.

Если
вектор начинается не из начала координат, то для определения его
координат можно провести его из начала координат, совместив с точкой
O начало вектора.

Правила
нахождения координат результирующего вектора:

1.
При суммировании двух и более векторов каждая координата
результирующего вектора равна сумме соответствующих координат
заданных векторов. Если даны два вектора

(x₁; y₁;
z₁) и

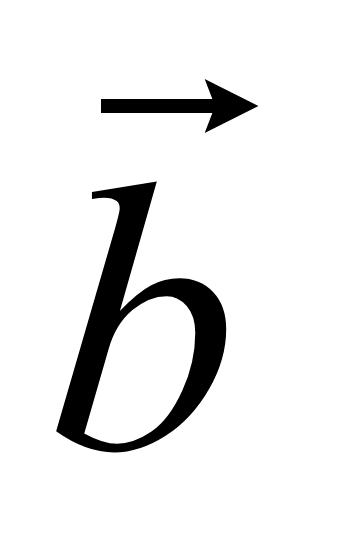
(x₂; y₂;
z₂), то сумма векторов

+

дает вектор с координатами (x₁ +
x₂; y₁
+ y₂; z₁
+ z₂)

+

= (x₁ + x₂;
y₁ + y₂;
z₁ + z₂).

2.
Разность является разновидностью суммы, поэтому разность
соответствующих координат дает каждую координату вектора, полученного
при вычитании двух заданных векторов. Если даны два вектора

(x_a;
y_a;
z_a) и

(x_b;
y_b;
z_b),
то разность векторов

—

дает вектор с координатами (x_a
— x_b;
y_a —
y_b; z_a
— z_b)

—
= (x_a
— x_b;
y_a —
y_b; z_a
– z_b).

3.
При умножении вектора на число каждая координата результирующего
вектора равна произведению этого числа на соответствующую координату
заданного вектора. Если даны число k и
вектор

(x;
y; z), то
умножение вектора на число k дает вектор k

с координатами

k

= (kx; ky; kz).

Задача.
Найти координаты вектора

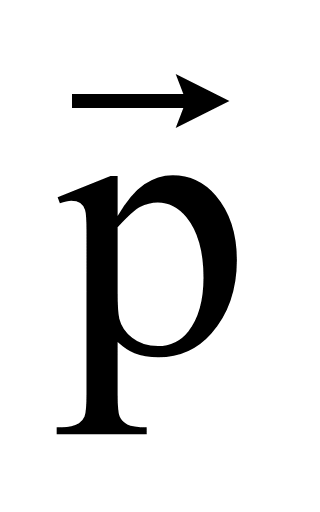
= 2

— 3
+
4
,
если координаты векторов

(1; -2; -1),

(-2; 3; -4),

(-1; -3; 2).

Решение

=
2

+ (-3
)
+ 4

2

= (2·x_a;
2·y_a;
2·z_a)
= (2·1; 2·(-2); 2·(-1)) = (2; -4; -2);

-3
=
(-3·x_b;
-3·y_b;
-3·z_b)
= (-3·(-2); -3·3; -3·(-4)) = (6; -9; 12);

4
=
(4·x_c;
4·y_c;
4·z_c)
= (4·(-1); 4·(-3); 4·2) = (-4; -12; 8).

=
(2 + 6 — 4; -4 — 9 -12; -2 + 12 + = (4; -25; 18).

#Векторное произведение

Векторное произведение (англ. cross product, также называется косым или псевдоскалярным) для двух векторов равно произведению их длин и синуса угла между ними — причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:

Так же, как и со скалярным произведением, доказательство координатной формулы оставляется упражнением читателю. Если кто-то захочет это сделать: это следует из линейности обоих произведений (что в свою очередь тоже нужно доказать) и разложения по базисным векторам $\overline{(0, 1)}$ и $\overline{(1, 0)}$.

Геометрически, это ориентированная площадь параллелограмма, натянутого на вектора $a$ и $b$:

Его свойства:

• Векторное произведение антисимметрично: $a \times b = — (b \times a)$.
• Коллинеарные вектора имеют нулевое векторное произведение.
• Если $b$ «слева» от $a$, то векторное произведение положительное.
• Если $b$ «справа» от $a$, то векторное произведение отрицательное.

Для него обычно тоже перегружают оператор — либо , либо :

Примечание. Вообще говоря, формально векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но пока в нашем двумерном мире об этом думать не надо.

Скалярное и векторное произведения тесно связаны с углами между векторами и могут использоваться для подсчета величин вроде ориентированных углов и площадей, которые обычно используются для разных проверок.

Когда они уже реализованы, использовать произведения гораздо проще, чем опираться на алгебру. Например, можно легко вычислить угол между двумя векторами, подставив в знакомый нам векторное и скалярное произведение:

В дальнейшем, свойства произведений помогут нам в определении взаимного расположения точек и, например, прямой, поэтому важно эти свойства понять и крепко запомнить