Прямоугольник, ромб, квадрат

Площадь четырёхугольников

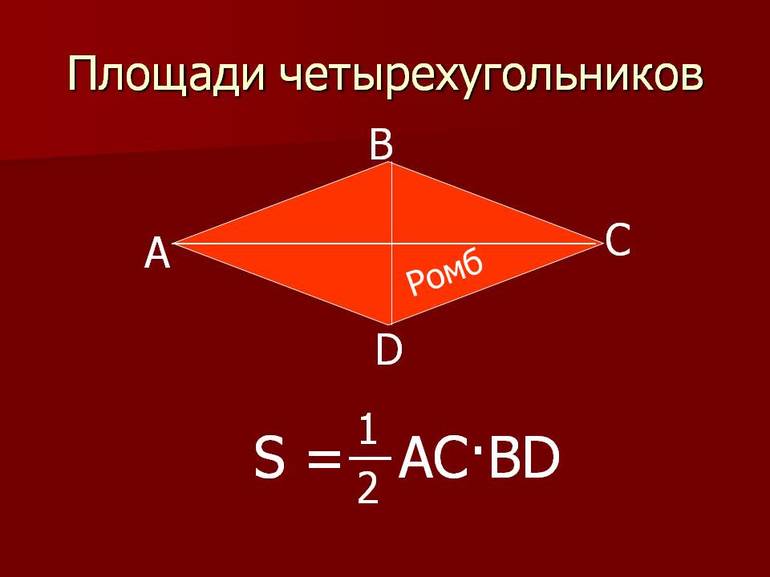
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.

К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.

Квадрат и прямоугольник

Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a 2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.

Параллелограмм, ромб и трапеция

Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.

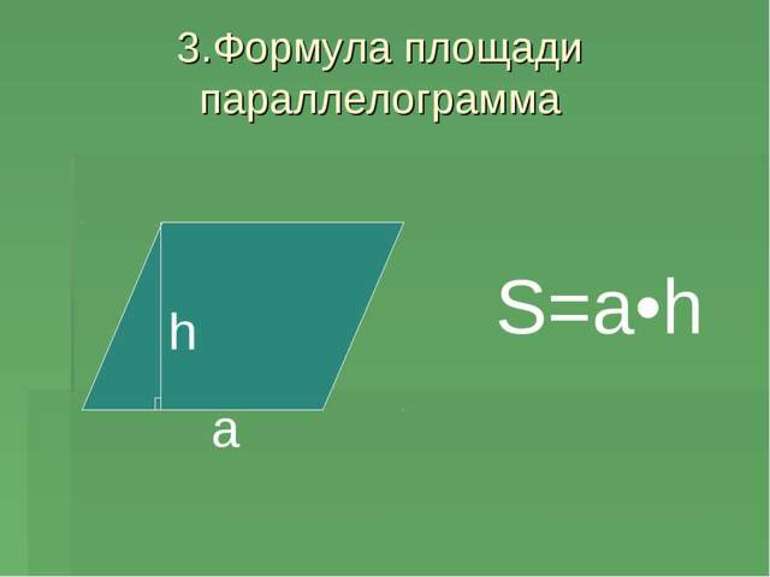
Применяются три формулы площади параллелограмма:

Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:

Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.

В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).

В этой формуле имеются следующие обозначения:

Выпуклый четырёхугольник

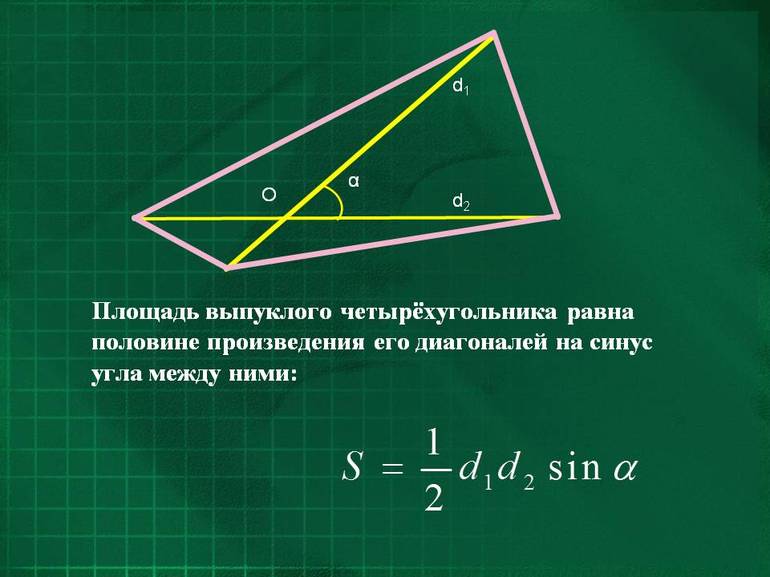
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.

Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.

В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:

Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).

Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos 2 γ.

Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.

Раздел 5. Векторы

Абсолютная величина и направление вектора

Вектор — это направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, b, с, … . Можно также обозначать вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта.

Векторы АВ и CD называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы АВ и CD называются противоположно направленными, если полупрямые АВ и CD противоположно направлены.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (0). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Равенство векторов

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что

равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Координаты вектора

Пусть вектор а имеет началом точку А1 (х1; у1), а концом точку А2 (х2; у2). Координатами вектора а будем называть числа а1 = х2 – х1, а2 = у2 – у1. Координаты нулевого вектора равны нулю.

Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.

Сложение векторов

Суммой векторов а и b с координатами а1, а2 и b1, b2 называется вектор с с координатами a1 +b1, a2 + b2.

Теорема 10.1. Каковы бы ни были точки А, В, С, имеет место векторное равенство АВ + ВС = АС.

Сложение сил

Силу, приложенную к телу, удобно изображать вектором, направление которого совпадает с направлением действия силы, а абсолютная величина пропорциональна величине силы. Как показывает опыт, при таком способе изображения сил равнодействующая двух или нескольких сил, приложенных к телу в одной точке, изображается суммой соответствующих им векторов.

Представление силы в виде суммы сил, действующих в двух заданных направлениях, называется разложением силы по этим направлениям. Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси.

Умножение вектора на число

Произведением вектора (а1; а2) на число λ называется вектор (λа1; λа2).

Теорема 10.2. Абсолютная величина вектора λа равна |λ| |a|. Направление вектора λа при а ≠ 0 совпадает с направлением вектора а, если λ > 0, и противоположно направлению вектора а, если λ < 0.

Разложение вектора по двум неколлинеарным векторам

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы направлены либо одинаково, либо противоположно.

Пусть а и b — отличные от нулевого неколлинеарные векторы, тогда любой вектор с можно представить в виде с = λа + ɳb.

Скалярное произведение векторов

Скалярным произведением векторов a(a1; a2) и b(b1; b2) называется число а1b1 + а2b2. Скалярное произведение а • а обозначается а2 и называется скалярным квадратом.

Для любых векторов а(а1; а2), b(b1; b2), с(с1; с2)(а + b) • с = ас + bс.

Теорема 10.3. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нулевого векторов равно нулю, то векторы перпендикулярны.

Разложение вектора по координатным осям

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Для любого вектора a (a1; а2) получается разложение а = а1е1 + а2е2.

Вы смотрели «Геометрия 8 Погорелов: все теоремы и определения» — краткое повторение геометрии за 8 класс (основные понятия, определения и теоремы без доказательств).

Развернутый угол

Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.

Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.

Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.

Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.

А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.

Прямоугольник

Определение прямоугольника известно с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что же такое параллелограмм?

Несмотря на заковыристое название, эта фигура столь же проста, как и прямоугольник. Параллелограмм это выпуклый четырехугольник, стороны которого попарно равны и параллельны.

В определении обязательно выделять слово выпуклый. Поскольку выпуклые и невыпуклые четырехугольники четко разделяются в геометрии. Причем невыпуклые фигуры вообще не изучаются в школьном курсе математики, так как они куда более непредсказуемы в своих свойствах.

Рис. 1. Выпуклые четырехугольники

Прямоугольник это частный случай параллелограмма. При этом существуют и другие частные случаи параллелограмма, например, ромб; и еще один особенный частный случай прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

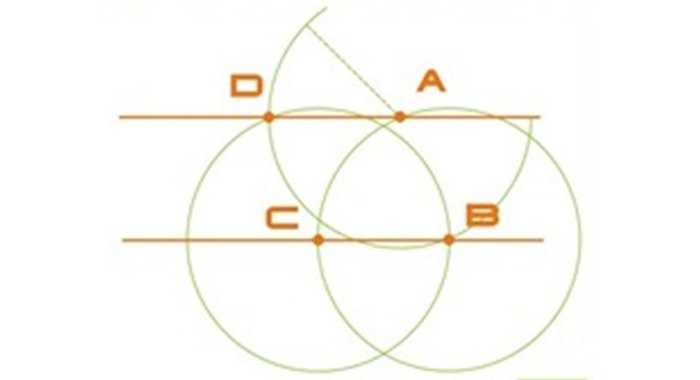
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Задача решена.

Прямоугольник

Определение 3

Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник

Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$

Рассмотрим два свойства прямоугольника.

Свойство 3: Обе диагонали прямоугольника равны между собой.

Доказательство.

Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.

Рисунок 2.

Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем

Так как $\angle B=\angle A={90}^0$, а $AB$ — общая сторона, то по I признаку равенства треугольников, $\triangle ABD=\triangle ABC$. Следовательно

Свойство доказано.

Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.

Доказательство.

Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).

Из свойства $2$ параллелограмма и равенства его диагоналей, получим

Так как $\angle DRC=\angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $\triangle DRC=\triangle ARB$. Значит, $\angle RDC=\angle RCD=\angle RAB={\rm \ }\angle RBA$.

Так как $\angle DRA=\angle CRB$, как вертикальные, то по I признаку равенства треугольников $\triangle DRA=\triangle CRB$. Значит, $\angle RDA=\angle RAD=\angle RCB={\rm \ }\angle RBC$.

Следовательно, $\angle A=\angle B=\angle C=\angle D$.

Так как сумма углов четырехугольника равняется ${360}^0$, то

Значит, по определению $3$, $ABCD$ является прямоугольником.

Свойство доказано.

Как описать четырехугольник окружностью?

Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.

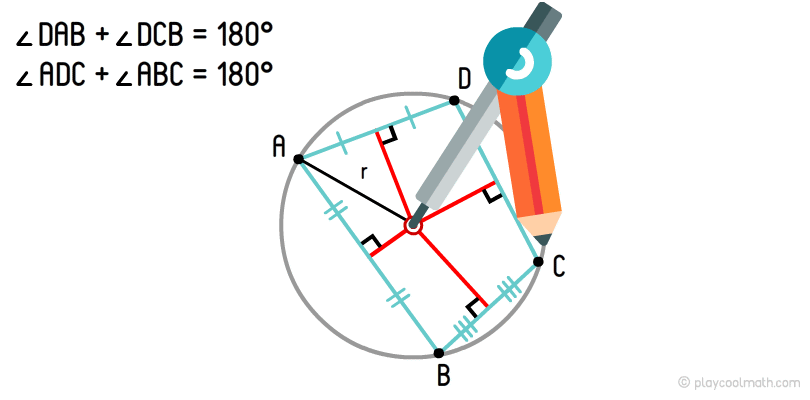Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.

Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.

Найди ортодиагональные четырехугольники.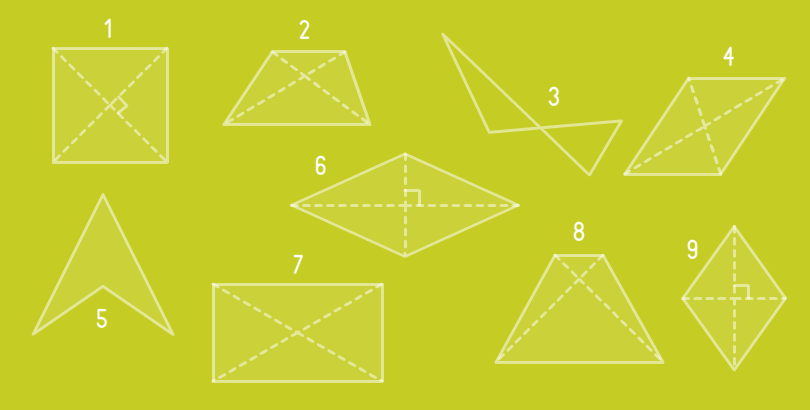

• #1
• #6
• #9

Математика. 5 класс

Конспект урока

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок. Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА

При этом точки А и В называют концами отрезка АВ

Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

• Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
• Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
• Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
• Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

1) а – это прямая.

2) АВ – это отрезок.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Основные понятия

В рамках вопроса измерения углов, в данном разделе рассмотрим несколько понятий, относящихся к начальным геометрическим сведениям:

• угол;
• развёрнутый и неразвёрнутый угол;
• градус, минута и секунда;
• градусная мера угла;
• прямой, острый и тупой углы.

Углом называют такую геометрическую фигуру, которая представляет собой точку (вершину) и исходящие из неё два луча (стороны). Угол называют развёрнутым, если оба луча лежат на одной прямой.

Благодаря градусной мере угла можно произвести измерение углов. Измерение углов проводится аналогично измерению отрезков. Так же, как и при измерении отрезков, при измерении углов используется специальная единица измерения. Чаще всего это градус.

Определение 1

Градус — это единица измерения. В геометрии он представляет собой угол, с которым сравнивают другие углы. Градус равен $\frac{1}{180}$ от развёрнутого угла.

Теперь можно дать определение градусной мере угла.

Определение 2

Градусная мера угла — это такое положительное число, которое обозначает, сколько раз градус помещается в данном угле.

Для измерения углов используют транспортир.

Пример записи градусной меры: $\angle ABC = 150^{\circ}$. На рисунке эта запись означает следующее:

В устной форме говорят так: «Угол АВС равен 150 градусам».

Некоторые части градуса имеют свои специальные названия. Минутой называют $\frac{1}{60}$ часть градуса, для обозначения используется знак $»$. Секундой называют $\frac{1}{60}$ часть минуты, для обозначения используют $»»$. Пример записи угла в 75 градусов, 45 минут и 28 секунд: $75^{\circ}45″28″»$.

Равными называют те углы, у которых градусные меры равны. Соответственно, углы можно сравнивать, говоря, что один угол меньше другого или один угол больше другого.

Выше было дано определение развернутому углу. Владея понятием градусной меры, мы можем описать разницу между развернутым и неразвернутым углом. Развернутый угол всегда равен $180^{\circ}$. Неразвернутый угол — это любой угол меньше $180^{\circ}$.

Различают прямой, острый и тупой углы. Прямой угол равен $90^{\circ}$, острый — меньше $90^{\circ}$, тупой — больше $90^{\circ}$ и меньше $180^{\circ}$.

Рисунок 4. Прямой, острый и тупой углы. Автор24 — интернет-биржа студенческих работ

В повседневной жизни есть примеры необходимости и важности умения измерять углы и понимать градусную меру. Измерение углов необходимо в различных исследованиях, в том числе в астрономии при определении положения небесных тел. Для практики, попробуйте начертить хотя бы три неразвёрнутых угла и один развёрнутый разными способами, измерьте с помощью транспортира углы и запишите эти результаты

Можно задать случайные числа и попрактиковаться в точности черчения углов с помощью транспортира, деления их с помощью биссектрисы (биссектриса — это луч, исходящий из вершины данного угла и делящий угол пополам)

Для практики, попробуйте начертить хотя бы три неразвёрнутых угла и один развёрнутый разными способами, измерьте с помощью транспортира углы и запишите эти результаты. Можно задать случайные числа и попрактиковаться в точности черчения углов с помощью транспортира, деления их с помощью биссектрисы (биссектриса — это луч, исходящий из вершины данного угла и делящий угол пополам).

Все о параллелограмме

Чем отличаются свойства от признаков?Свойства нельзя путать с признаками, хоть они и очень похожи. Например, свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, а признаки предназначены для выявления параллелограммов среди четырехугольников.

Свойства параллелограмма

1. Противолежащие стороны равны.

2. Противолежащие стороны параллельны.

3. Диагонали пересекаются и точкой пересечения делятся пополам.

4) Сумма углов прилежащих к любой стороне равна 180°. 

Это так, потому что, как в примере на картинке, стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 180°.

5) Противолежащие углы попарно равны. Это доказывается через третий признак равенства треугольников, ведь, например, у треугольников ABD и BDC все стороны равны, а значит и углы тоже.

Теперь перейдем к признакам параллелограмма. Это то, что нам помогает понять, что четырехугольник является параллелограммом.

У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.

Признаки параллелограмма

1. Две противоположные стороны четырехугольника параллельны и равны.

2. Противоположные стороны четырехугольника попарно равны.

3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Теперь рассмотрим биссектрису в параллелограмме.

Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Рассмотрим два полезных факта, связанных с биссектрисой в параллелограмме.

1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник. 

Это тоже доказывается с помощью параллельных прямых. Рассмотрим две параллельные прямые: AD и BC, а также секущую AF. Углы FAD и BFA равны, так как они накрест лежащие. А так как AF — биссектриса, то углы BAF и FAD, углы FAD и BFA тоже, значит и BAF = BFA. Следовательно, треугольник BAF — равнобедренный.

2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

Мы почти закончили изучение параллелограмма. Осталось только рассмотреть формулы для нахождения площади. Их всего три.

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

2. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

3. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Какая фигура является антагонистом параллелограмма?Есть такая фигура, которая называется «антипараллелограмм». Это плоский и самопересекающийся четырехугольник, в котором две противоположные стороны равны между собой, но не параллельны. Напомним, что у параллелограмма противоположные стороны равны и параллельны между собой.

Мы рассмотрели всю теорию, связанную с параллелограммом. Давайте теперь решим задание для закрепления материала.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Стороны параллелограмма равны 10 и 15. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение. Примем искомую высоту за x. Как мы уже знаем, площадь параллелограмма можно найти с помощью высоты и стороны, к которой эта высота проведена. Соответственно, с помощью этой формулы мы и можем найти x:\(S = a*h_1=b*h_2\)\(S=10*12=15*h_2\)\(h_2=\frac{10*12}{15}\)\(h_2=8\)Ответ: 8

На этом мы закончили изучение параллелограмма, так что можем двигаться дальше!

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

. То есть, если угол между линиями A .

равен φ, то мы говорим, что угол между пересекающимися прямыми a и b равен φ.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Угол между прямыми»

Докажем, что угол между двумя пересекающимися прямыми не зависит от выбора точки M

Возьмем любую другую точку M₁A₁и через него линии a₁и б

параллельны a и b соответственно. Пусть угол между прямыми a

и б

быть

и угол между линиями a

и б₁один₁B₁Если линии a

лежат в одной плоскости, то по свойству углов пересечения для параллельных прямых угол α₁B₁равна φ и равна углу a.₁B₁Пусть теперь линии a

и б₁.

которые пересекаются в точке M₂лежат в одной плоскости. И пусть линии₂и б₂которые пересекаются в точке M₁и б₁Поскольку линия a₁параллельна прямой a и прямой a₂и б₂Поскольку линия a₂.

также параллельны. Поскольку линия b₁, b₁, a₂, b₂параллельна прямой b и прямой b₁параллельна прямой b, то согласно принципу параллельности прямых в пространстве, прямые b₂.

Ответственный, настойчивый, харизматичный, последовательный, очень хороший уровень подготовки, терпеливый. Наша дочь очень довольна и, очевидно, Intere₁Большое спасибо. Я очень рада, что мы нашли этот источник для обучения. Ирина Сергеевна объясняет все быстро, четко и динамично. Всего за несколько уроков мы наверстали упущенную химию и продвинулись вперед. Мы обязательно обратимся снова в будущем.₂Елизавета делает хорошие успехи и учится с радостью и энтузиазмом. Римма Николаевна очень интересно преподносит материал. Мне очень нравится этот учитель, мы очень довольны уроками.₁Нам нравилась Нина Ивановна, хороший человек и прекрасный учитель. Она очень ответственная, трудолюбивая и знающая. Она сразу же нашла подход к своему ученику. Она может доходчиво объяснить любую тему. Учитель, в отличие от многих других преподавателей, не тратит время впустую, а действительно помогает.₂Она была прекрасным преподавателем и нашла подход с первых же уроков. Она объяснила все очень четко и понятно. Моему ребенку она очень нравится, и он просит о дополнительных занятиях.₁Здравствуйте, Рита Ивановна очень профессионально оценила все пробелы в знаниях моего сына, и мы бы с удовольствием продолжили обучение с ней! Уроки очень хорошие, преподаватель все понятно объясняет, я рекомендую ее всем.₂Спасибо, Ольга Ольга, за урок на каникулах. Желаю ей здоровья и благополучия, побольше счастливых событий в жизни, процветания, успехов и удачи в ее нелегком и нужном труде. Спасибо за урок, мне он очень понравился!₁и б₂