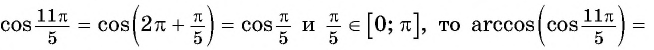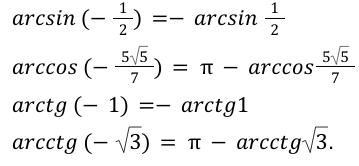Арксинус числа
Определение 1
Арксинус числа $x$ — это множество значений углов, для которых $sinα = x$. Также определение арксинуса можно записать так: $arcsin(x) = α$.
Рассмотрим рисунок 1, на котором изображена окружность с радиусом, равным единице. Как мы помним, $sinα$ — это отношение противолежащей стороны к гипотенузе, численно он равен длине стороны $AC$. Так как арксинус его обратная функция и есть не что иное как угол, от которого берётся синус, свойства арксинуса очень похожи на свойства синуса:
- Область определения функции арксинуса $D(y)= \ $, для синуса $D(y)=\ $;
- Область значения для арксинуса $E = \ $, для синуса $E = \ $
- Функции синуса и арксинуса обе возрастающие;
- Функции арксинуса и синуса обе нечётные, то есть: $arcsin(-x)= -arcsinx$;
- Функция $y=arcsin(x)$ равна нулю при $x=0$.
График арксинуса выглядит следующим образом:
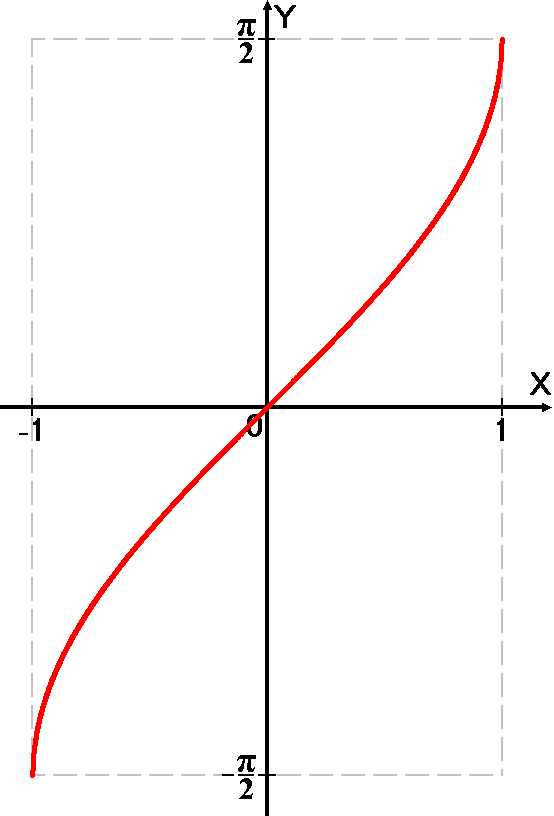 Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ
Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ
Примеры
Одно число
| Формула | Описание | Результат |
|---|---|---|
| Cos( 1.047197 ) | Возвращает косинус 1,047197 радиана или 60 градусов. | 0.5 |
| Cot( Pi()/4 ) | Возвращает котангенс 0,785398… радиана или 45 градусов. | 1 |
| Sin( Pi()/2 ) | Возвращает синус 1,570796 радиана или 90 градусов. | 1 |
| Tan( Radians(60) ) | Возвращает тангенс 1,047197… радиана или 60 градусов. | 1.732050… |
| Acos( 0.5 ) | Возвращает арккосинус аргумента 0,5 в радианах. | 1.047197… |
| Acot( 1 ) | Возвращает арккотангенс аргумента 1 в радианах. | 0.785398… |
| Asin( 1 ) | Возвращает арксинус аргумента 1 в радианах. | 1.570796… |
| Atan( 1.732050 ) | Возвращает арктангенс аргумента 1,732050 в радианах. | 1.047197… |
| Atan2( 5, 3 ) | Возвращает арктангенс угла (который составляет приблизительно 31 градус) между осью Х и линией, проходящей через точку начала координат (0, 0) и точку с координатами (5, 3). | 0.540419… |
| Atan2( 4, 4 ) | Возвращает арктангенс угла (который составляет ровно π/4 радиана или 45 градусов) между осью Х и линией, проходящей через точку начала координат (0, 0) и точку с координатами (4, 4). | 0.785398… |
| Degrees( 1.047197 ) | Возвращает число в градусах, соответствующее 1,047197 радиана. | 60 |
| Pi() | Возвращает трансцендентное число π. | 3.141592… |
| Radians( 15 ) | Возвращает число в радианах, соответствующее 15 градусам. | 0.261799… |
Таблица с одним столбцом
В примерах этого раздела используется источник данных с именем ValueTable, который содержит следующие данные. Последняя запись в таблице — π/2 радиана или 90 градусов.
| Стоимость |
|---|
| 0.5 |
| -2 |
| 1.570796… |
Некоторые другие формулы
Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin, arccos, arctg и arcctg, еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.
Для примера возьмем формулу половинного угла . Если добавить условие, что величина угла альфа принадлежит отрезку от нуля до пи, то будет справедливо равенство . При указанном условии угол альфа можно заменить на арккосинус числа a, что нам даст формулу вида  , откуда можно получить следующую формулу, выражающую арккосинус через арксинус: .
, откуда можно получить следующую формулу, выражающую арккосинус через арксинус: .
Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin, arccos, arctg и arcctg.
В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin, arccos, arctg и arcctg, сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения.
Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x. Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
- Арксинус ( y = arcsin x )– это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .
- Арккосинус ( y = arccos x )– это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
- Арктангенс ( y = arctg x )– это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
- Арккотангенс ( y = arcctg x )– это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Расчет тангенса и котангенса в компьютерных программах
Тангенс и котангенс: что это такое?
Тангенс и котангенс — это тригонометрические функции, которые используются для нахождения соотношений между двумя сторонами прямоугольного треугольника.
Тангенс определяется как отношение противоположного катета к прилежащему, а котангенс как отношение прилежащего катета к противоположному.
В компьютерных программах расчет тангенса и котангенса выполняется с помощью математических функций. Обычно это функции «tan» и «cot». Например, если нужно найти тангенс угла в радианах, можно использовать следующий код: tan(x), где «x» — значение угла в радианах.
Зачем нужны тангенс и котангенс в компьютерных программах?
Тангенс и котангенс могут использоваться во многих приложениях, где необходимо вычислить углы или расстояния между объектами. Например, в компьютерной графике тангенс используется для определения наклона линий и кривых. В астрономии тангенс используется для нахождения высоты объектов на небосводе. Котангенс же применяется для определения угла наклона плоскости.
Также тангенс и котангенс могут использоваться в физике, инженерных расчетах и других научных приложениях
Важно понимать, что правильный расчет тангенса и котангенса может существенно влиять на точность результатов, поэтому необходимо использовать соответствующие математические функции и учитывать единицы измерения
Тангенс и котангенс нужны для решения задач, где требуется найти угол между двумя линиями или найти расстояние между двумя точками. В геометрии тангенс и котангенс используются для вычисления высоты, основания, площади и объема различных геометрических фигур.
Тангенс и котангенс: каковы их различия и зачем нужны
В геометрии довольно часто приходится сталкиваться с задачами, для решения которых необходимо знание тангенса и котангенса. Эти две математические функции очень важны как для геометрических вычислений, так и для работы в ряде других областей науки и техники.
Тангенс и котангенс являются соответственно функциями тригонометрии синуса и косинуса, разделяющихся каждая своей обратной функцией. Тангенс и котангенс — это отношения двух катетов в прямоугольном треугольнике, примыкающих к углу α и называемого соответственно катетом противоположным и катетом прилежащим.
Тангенс и котангенс находят применение в вычислениях астрономических координат, математической статистике, вероятности, физике, инженерии и многих других областях. Например, в радиотехнике тангенс и котангенс используются для вычисления импеданса и проводимости сигналов. В машиностроении они используются для нахождения углов наклона поверхностей и степени прессовки сжатых материалов.
Тангенс – это отношение стороны прямоугольного треугольника, противоположной заданному углу, к прилежащей стороне. Применение тангенса может быть очень разнообразным, он используется для решения уравнений, нахождения длины сторон треугольника, векторов, скорости и т. д.
Практическое применение тангенса и котангенса в физике и инженерии
Также котангенс применяется в оптике при расчетах нахождения фокусных расстояний линз.
06.06.2019 19:36:58
2019-06-06 19:36:58
Любые данныеЛюбые данныеЛюбые данные Любые данные
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения
принадлежащие промежутку
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):
Арккосинус есть число, заключенное в интервале от до , косинус которого равен .
Арксинус есть число, заключенное в интервале от до , косинус которого равен .
Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен Это число Используя это, получаем:
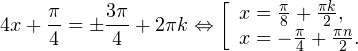
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
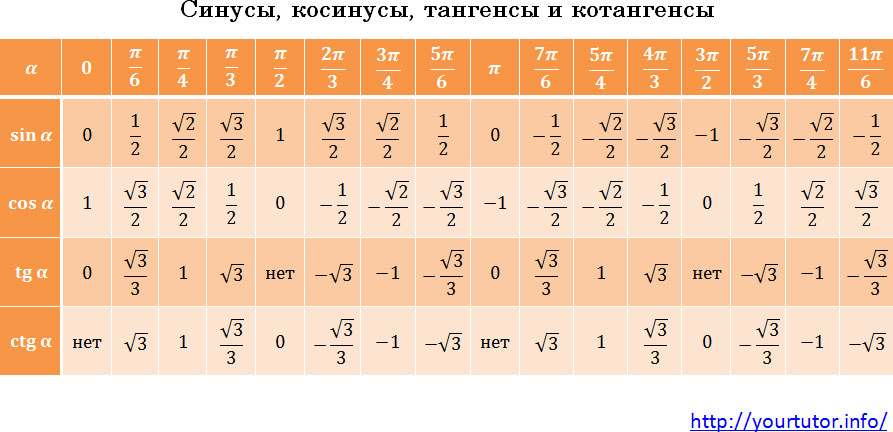
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку Воспользуемся для этого методом двойных неравенств. Вы помните, что и — целые числа:
1)
2)
Задача для самостоятельного решения №1. Найдите корни уравнения принадлежащие промежутку
Показать ответ
Ответ:
Арктангенс
Введем ф-цию, обратную тангенсу. Она называется арктангенс.
Напомним, что величину тангенса на координатной плоскости можно получить, если продолжить угол до его пересечения с вертикальной прямой х = 1. Аналогично, чтобы определить арктангенс некоторого числа а, надо отметить на этой прямой точку с координатами (1; а) и соединить её с началом координат:
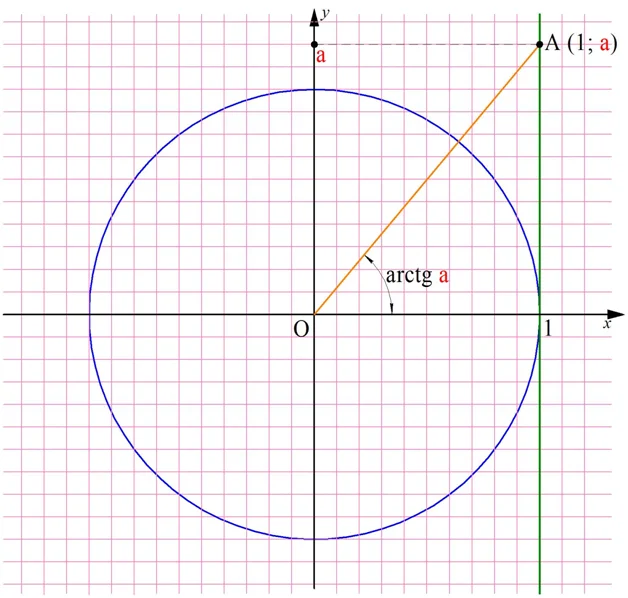
Несложно видеть, что, какое бы число а нами не было выбрано, мы с помощью построения всегда сможем соединить точку А с началом координат и получить некоторый угол arctga. Это значит, что область определения арктангенса – это вся числовая прямая, то есть промежуток (– ∞; + ∞).
Ещё раз уточним, что вводимые нами функции arcos, arcsin, arctg называются ОБРАТНЫМИ тригонометрическими функциями. C их помощью можно определить угол, если известно значение его синуса, косинуса или тангенса.Образно говоря, обратные триг-кие функции играют в тригонометрии ту же роль, что и квадратные корни при исследовании квадратных ур-ний. Как без квадратных корней невозможно решать квадратные ур-ния, так и без знания об обратных триг-ких функций нельзя решать уже тригом-кие уравнения.
Теперь вернемся к понятию арктангенса. При положительном значении числа а угол arctga будет принадлежать I четверти. Если же а – отрицательное число, то угол arctga окажется также отрицательным и будет принадлежать IV четверти:
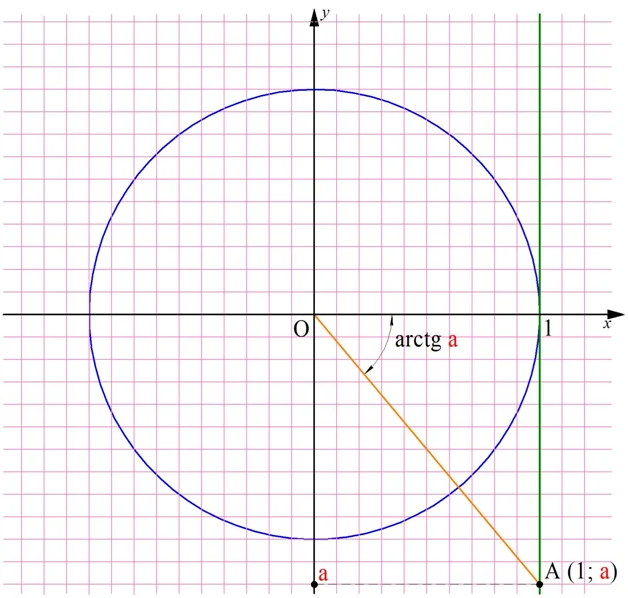
Получается, что величина arctgа может принадлежать промежутку (– π/2; π/2)
Обратите внимание, что в данном случае у промежутка круглые скобки. Действительно для углов (– π/2) и π/2 тангенс не определен, а потому арктангенс не может принимать эти два значения

Задание. Чему равен arctg 1?
Решение. Из таблицы тангенсов мы знаем, что tgπ/4 = 1. Это значит, что
Для вычисления арктангенсов отрицательных чисел используют формулу
В ее справедливости можно убедиться, взглянув на рисунок:
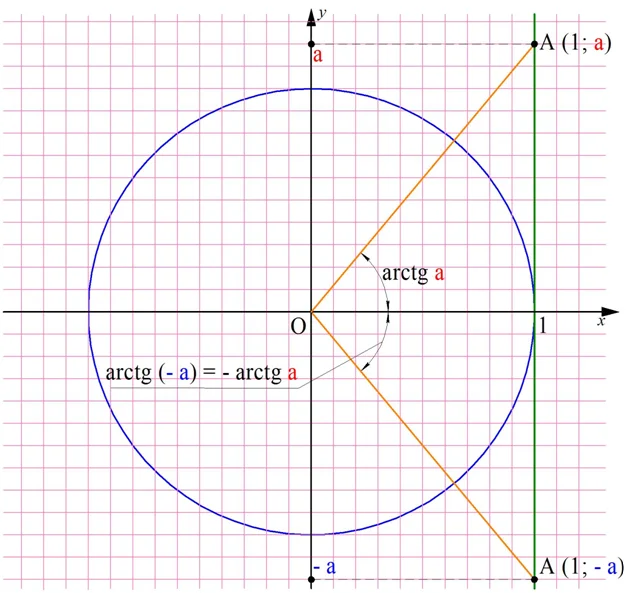

Задание. Вычислите arctg (– 1).
Решение.
Ответ: – 1
В принципе можно ввести ещё ф-цию, обратную котангенсу – арккотангенс. Однако для решения тригонометрических уравнений, как мы убедимся далее, она не требуется, а поэтому в рамках школьного курса математики ее можно не изучать.
В заключение приведем таблицы, которые помогают вычислять значение обратных тригон-ких функций:
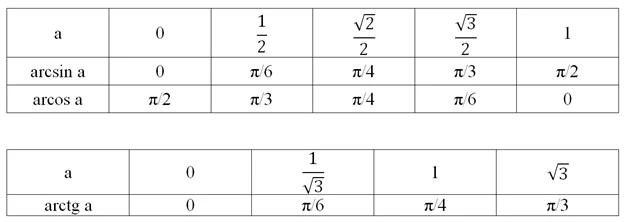
Противоположные значения для обратных значений функций арксинус, арккосинус, арктангенс, арккотангенс
Взаимосвязь функций противоположных чисел можно записать в следующем виде:

Перейдем к доказательству записанных выражений.
Доказательство арксинусов:
\
Данная тригонометрическая функция имеет предел значений от \ и синус его равен -a.
Докажем, что — arcsin a находится в пределах \ и обоснуем, что sin (-arcsin a)=-a.
Для функции арксинус справедливо неравенство, следующего вида:\.
Для того чтобы получить эквивалентное неравенство, нужно обе части равенства умножить на значение-1. После вычислений получим:\.
Докажем, что sin ( − arcsin a ) = − a sin(-arcsin a)=-a.
Применим свойство противоположных углов и составим уравнение:
sin ( − a r c sin a ) = − sin ( a r c sin a )=-sin arcsin a.
Арккосинус доказывается следующим образом:
Записываем выражение: \
Для этой функции принимает равенство \ обе части равенства нужно перемножить на значение равное -1 и изменить знаки на противоположные. Выполнив вычисления получим равенство: \.
Чтобы доказать оставшиеся две функции, применяются аналогичные свойства и правила.
Правило противоположных чисел позволяет упростить процесс решения и исключает все операции при вычислении с отрицательными числами.
Например:
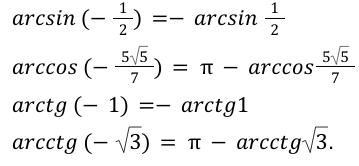
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<><><><>
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
sinα=tgα1+tgα, -π2
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
sinα=11+ctg2α, 0
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<><π2 следует,=»»>
- Из cosα=ctgα1+ctg2α, 0<><>
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<><π2. получаем=»» tg(arcsin α)=»sin(arcsinα)1-sin2(arcsinα)=α1-α2″ при=»» условии,=»» что=»»><>
- Исходим из tgα=1-cos2αcosα, α∈, получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Главные значения: arcsin, arccos, arctg и arctg
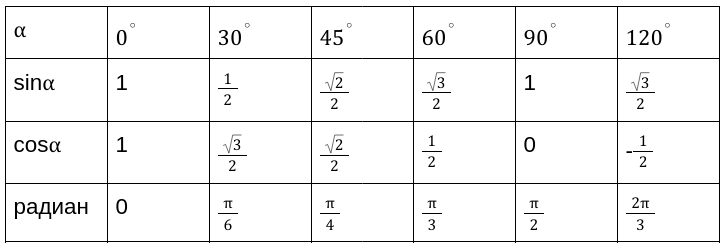
Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \ градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.
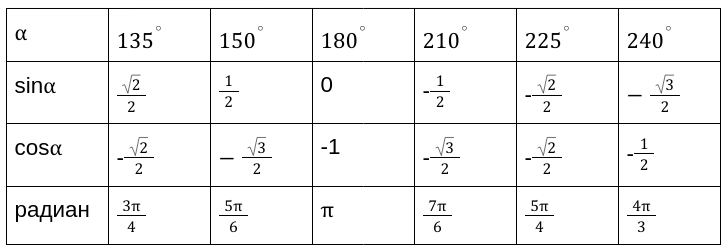 Продолжение таблицы 1
Продолжение таблицы 1
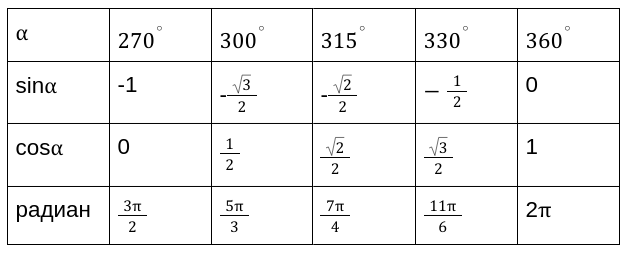
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.
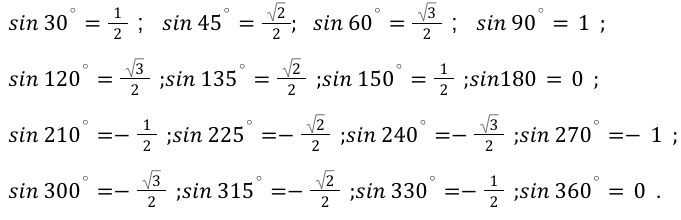
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.

Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.
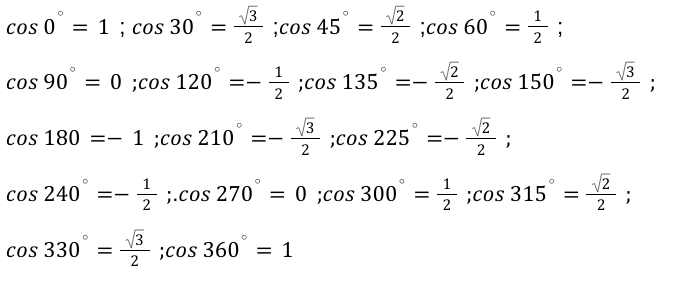
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.
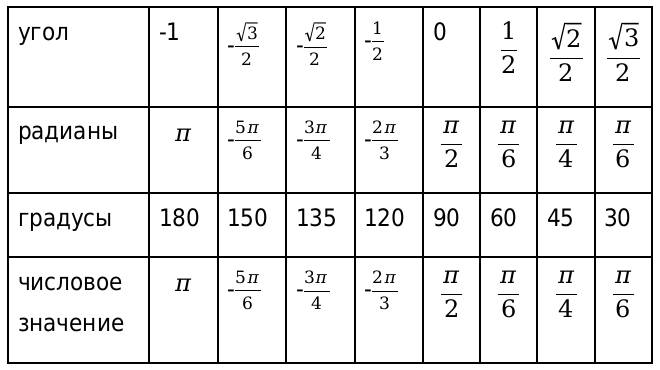
И напоследок остается вычислить значения арктангенса и арккотангенса.
Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:
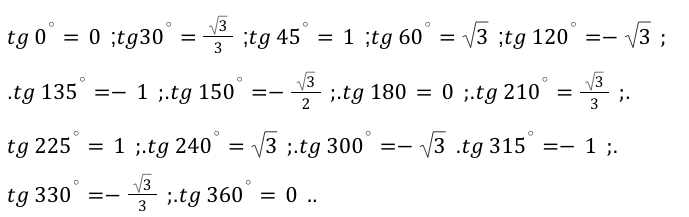
\ — данные угловые значения, не определяются, согласно основным законам геометрии и математики.
\- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются
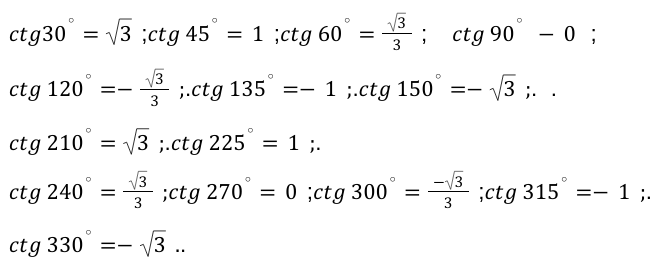
Далее все данные запишем в виде табличной формы.
Первая таблица для арктангенса
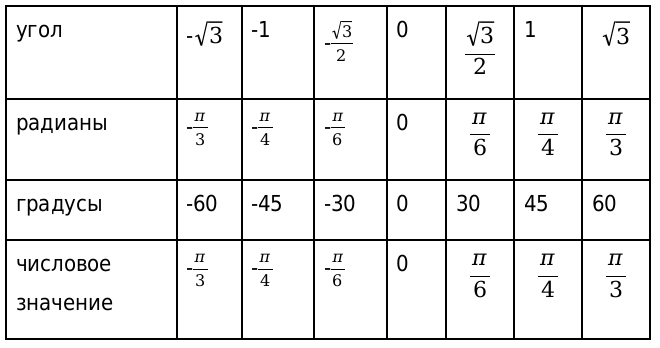
Вторая таблица для арккотангенса
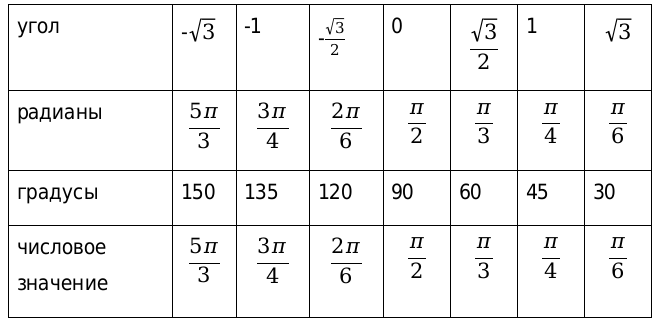
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
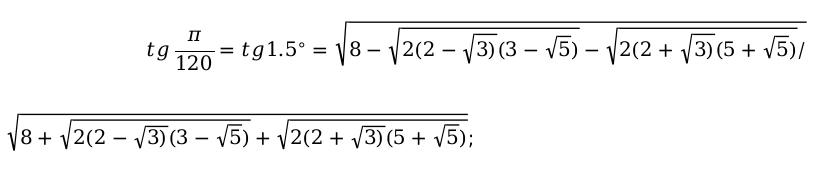
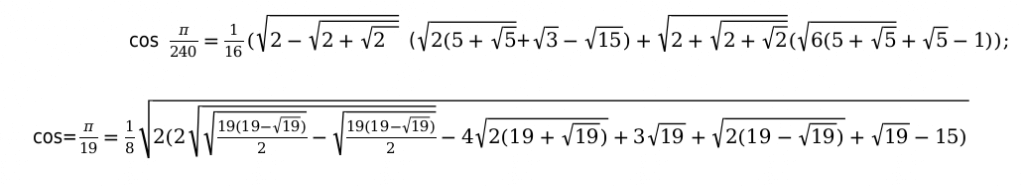
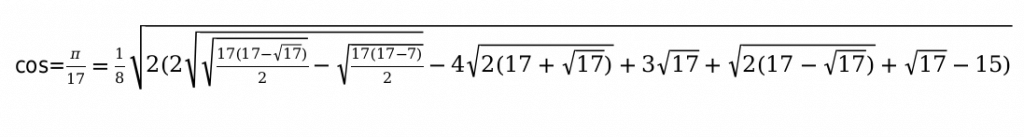
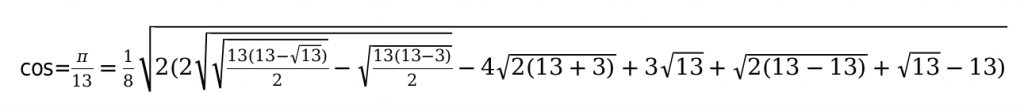
Основные способы, которые помогут заполнить таблицу функций тригонометрии.
Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции
Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec)
На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения.
Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.
В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.


Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:
\
Пример решения:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102
\
Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение. Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.

Арксинус (y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
| Свойства функции | Функции y=arcsin х |
| E(f) | \ |
| D(f) | \ |
| наличие четности | Нечётная, т.к. arcsin(-x)= — arcsin x |
| характер графика направление | возрастание |
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y).
| Свойства | Функции y=arccos х |
| E(f) | \ |
| D(f) | \ |
| Чётности | Данное свойство ей не характерно. Иными словами отсутствует. |
| Монотонность | Убывающая |
Арктангенс ( y = arctg x ) – характеризуется, как обратное значение функции относительно тангенса.
Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | \ | \ |
| Характер функции | Нечётная | Нечётная |
| Периоды | Возрастающая | Убывающая |
2.4.3. document.write(‘Обратные тригонометрические функции’); window.top.document.title = «2.4.3. Обратные тригонометрические функции»;
Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам
и
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента
существует единственный элемент
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу соответствует единственный элемент
и наоборот, каждому элементу
соответствует единственный элемент Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается
и каждому элементу
ставит в соответствие такой элемент
что f (x) = y; этот факт записывают так:
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции:
Область значений обратной функции совпадает с множеством определения самой функции:
Рассмотрим функцию f (x) = sin x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
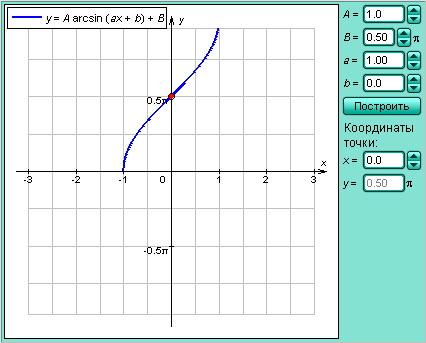
Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
| Рисунок 2.4.3.1.Арксинус |
 |
|
Модель 2.11. Функция y = arcsin x |
Аналогично, на промежутке D (f–1) = E (f) = можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) =
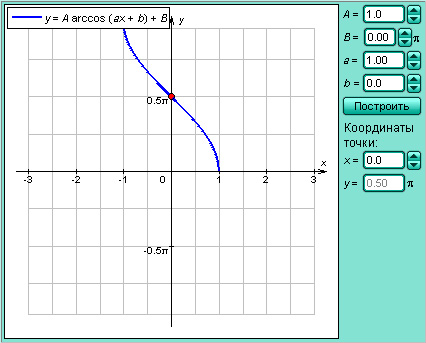
Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
| Рисунок 2.4.3.2.Арккосинус |
 |
|
Модель 2.12. Функция y = arccos x |
Рассмотрим функцию f (x) = tg x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
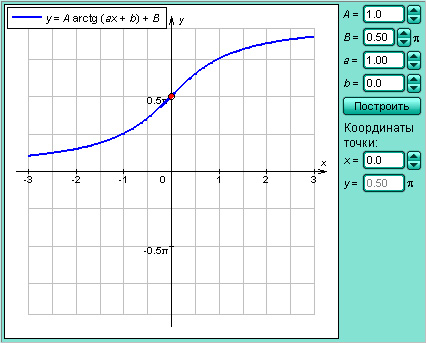
Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
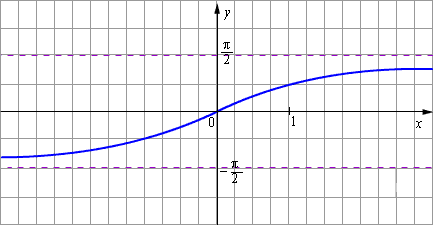 |
| Рисунок 2.4.3.3.Арктангенс |
 |
|
Модель 2.13. Функция y = arctg x |
Для построения арккотангенса выберем промежуток x (0; π). Тогда
Построим обратную функцию с областью определения
и областью значений
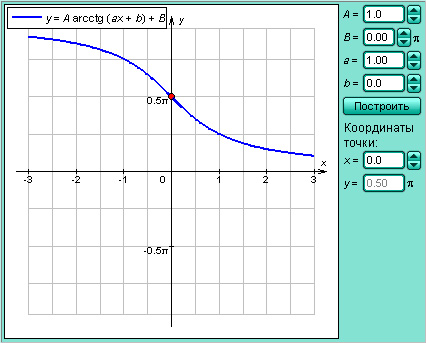
Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
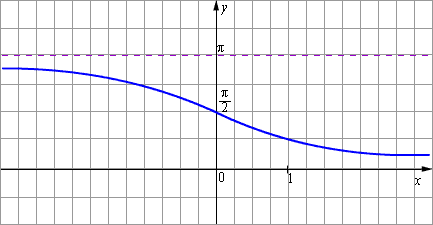 |
| Рисунок 2.4.3.4.Арккотангенс |
 |
|
Модель 2.14. Функция y = arcctg x |
Итак, запись b = arcsin a обозначает, что
и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
Пример 1
Докажите тождество
Показать решение
Пример 2
Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).
Показать решение
Как пользоваться таблицей
Алгоритм работы с таблицей довольно прост:
- В первом столбце выбираем значение угла (например, 30 градусов).
- В первой строке выбираем необходимую функцию (например, cos).
- Находим место их пересечение (в данном случае, 3/2).
Если Вам надо узнать значение обратных тригонометрических функций угла (arcsin, arccos, arctg, arcctg) необходимо совершить действия в обратном порядке:
- В первой строке выбираем функцию (если Вам известен arccos, то берем cos).
- Выбираем значение угла (например, -1).
- В первом столбце определяем угол, которому соответствует значение (в данном случае, 180 градусов).
Обратите внимание на то, что в таблице представлены стандартные тригонометрические углы (30, 60, 90, 180, 270 и 360 градусов). В ситуации, когда Вам дано другое значение (например, 87 градусов), рекомендуем воспользоваться нашими онлайн-калькуляторами
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<><>
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<><><>
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<>
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<>
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и=»» постараемся=»» вывести=»»>
Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 числа=»» арксинус=»» есть=»» и=»» это=»» –=»»></a<1>
Вывод: arcsina=arctga1-a2, -1<>
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Пример 3
Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<><>
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Нахождение значения аргумента
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки
ординаты которых равны
Этим точкам соответствуют углы
и
и таких углов бесконечно много. Однако, если рассмотреть промежуток то на нем функция
возрастает и принимает все значения от -1 до 1. Поэтому для любого числа
из промежутка
существует единственное число такое что
Так на промежутке
существует единственное значение аргумента, при котором значение функции равно — это угол равный
( рис.93)
Определение Арксинуса
Этот угол обозначают
Так, поскольку и
Вычислите:
Решение:
так как
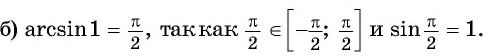
Пример №2
Найдите значение выражения:

Решение:
так как
![]()
(рис. 95, б).
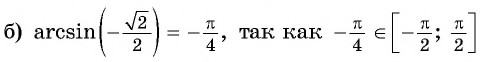
![]()
Заметим, что
( рис.95) Так как углы, соответствующие точкам
и
где
с ординатами
и
отличаются только знаком, то
для любого числа
(рис. 96).
Пусть
тогда
Так как точки
имеют противоположные ординаты, то
Поскольку то по определению арксинуса
Так как то для любого числа
Воспользуемся полученным равенством и найдем значение выражения
Так как 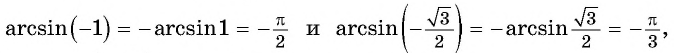
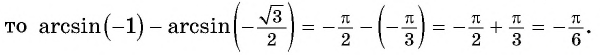
Отметим, что областью определения выражения
является отрезок Если
то выражение не имеет смысла.
Например, выражения не имеют смысла, так как
Выражение не имеет смысла, так как
Из определения арксинуса числа следует, что
если ![]()
Например, 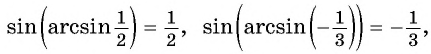
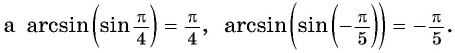
Рассмотрим промежуток на котором функция
возрастает и принимает все значения от до 1. Для любого числа из промежутка
существует единственное число такое, что
Определение Арккосинуса
Этот угол обозначают
Например: поскольку
и
Вычислите:
Решение:
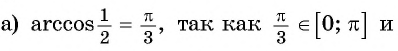
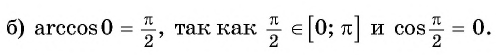
Пример №4
Найдите значение выражения:
Решение:
так как
( рис. 98.а)
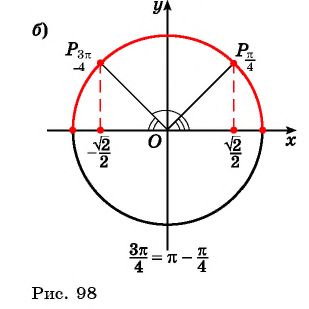
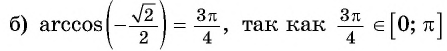
( рис.98.б)
Заметим, что 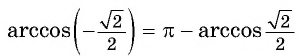
( см.98)
Пусть ![]()
Так как точки
имеют противоположные абсциссы, то
Поскольку то по определению арккосинуса
Так как ![]() для любого числа (рис. 99).
для любого числа (рис. 99).
Воспользуемся полученным равенством и найдем значение выражения
Так как ![]()
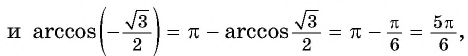
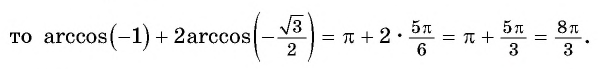
Областью определения выражения является отрезок
Если то выражение не имеет смысла.
Так, выражения
не имеют смысла, поскольку
![]()
Выражение
не имеет смысла, так как
Из определения арккосинуса числа следует, что
если и ![]()
Например, 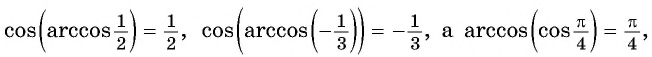
На промежутке монотонности функции существует единственный угол, тангенс которого равен некоторому данному числу
Определение Арктангенса
Этот угол обозначают
Так, поскольку и
Вычислите:
Решение:
так как
и
![]()
![]()
и
Для любого числа
верно равенство
(рис. 101).
Пример №6
Найдите значение выражения
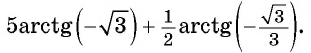
Решение:
Так как 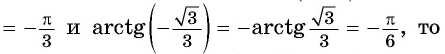
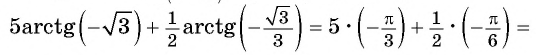
Из определения арктангенса числа следует, что
при 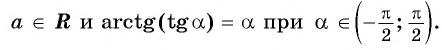
Например, 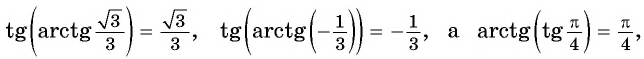
На промежутке монотонности
функции
существует единственный угол, котангенс которого равен некоторому данному числу
Определение Арккотангенса
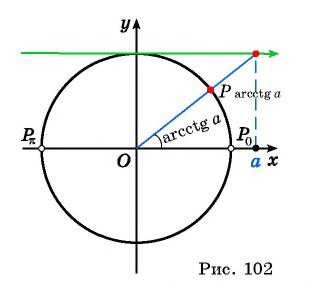
Этот угол обозначают
Например, поскольку
Вычислите:
Решение:
так как
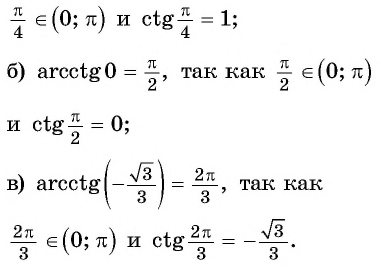
Для любого числа
верно равенство
(рис. 103).
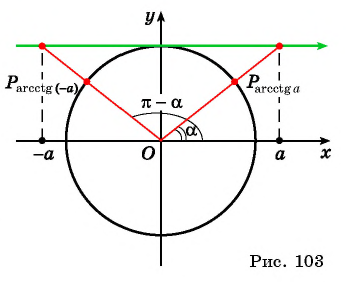
Пример №8
Найдите значение выражения
Решение:
Так как ![]()
![]()
Из определения арккотангенса числа следует, что
если
и ![]()
Например, ![]()
Примеры заданий и их решения
Верно ли, что:
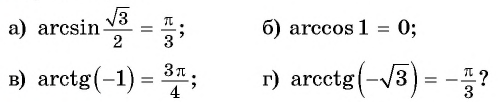
Решение:
- Верно, так как
- верно, так как
- неверно, так как
- неверно, так как
Вычислите:
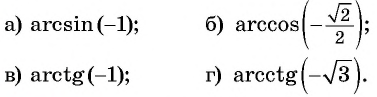
Решение:
![]()
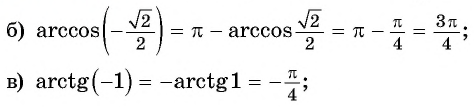
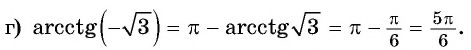
Найдите значение выражения:
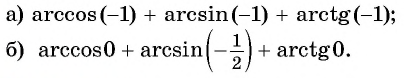
Решение:
![]()
![]()
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим: ![]()
Найдите область определения выражения:
![]()
Решение:
- По определению арксинуса числа
это угол, синус которого равен - По определению арккосинуса числа
это угол, косинус которого равен
Найдите значение выражения:
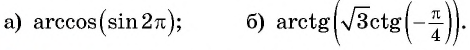
Решение:
![]()
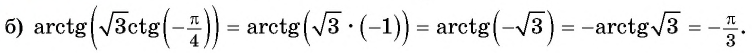
Вычислите
Решение:
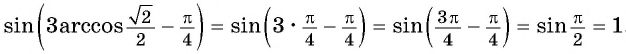
Найдите значение выражения
Решение:
Воспользуемся формулой
при
Поскольку
то эту формулу сразу применить нельзя.
Так как