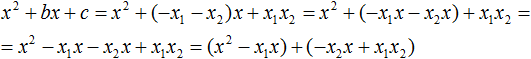Как решать линейные уравнения с одной переменной

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить .

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

x2 + bx + c

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x2 + bx + c можно разложить на множители следующим образом. Сначала b из уравнения x₁ + x₂ = −b. Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x2 + bx + c

Раскроем скобки там где это можно:

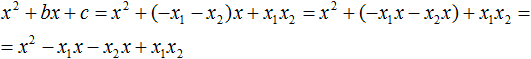
В получившемся выражении выполним . В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

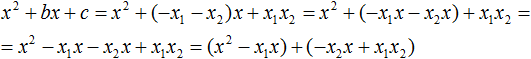
Из первых скобок вынесем общий множитель x, из вторых скобок — общий множитель −x₂

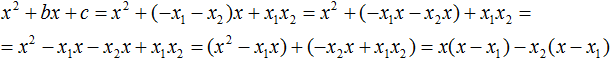
Далее замечаем, что выражение (x − x₁) является общим множителем. Вынесем его за скобки:

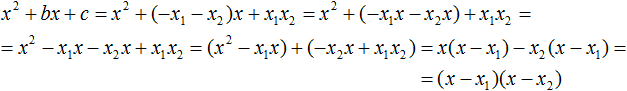
Мы пришли к тому, что выражение x2 + bx + c стало равно (x − x₁)(x − x₂)

x2 + bx + c = (x − x₁)(x − x₂)

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

ax2 + bx + c = a(x − x₁)(x − x₂)

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax2 + bx + c = 0, то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства и

Для начала выразим b и c. В первом равенстве умножим обе части на a. Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c. Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax2 + bx + c. Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂, которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Теперь из первых скобок вынесем общий множитель ax, а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a. Вынесем его за скобки. Его можно расположить в самом начале выражения:

Мы пришли к тому, что выражение ax2 + bx + c стало равно a(x − x₁)(x − x₂)

ax2 + bx + c = a(x − x₁)(x − x₂)

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂.

Что такое линейное уравнение с одной переменной

Уравнением называют какое-либо выражение минимум с одной переменной, части которого разделены знаком равенства.

Пример 1

Рассмотрим несколько наглядных примеров.

Пусть имеется выражение следующего вида: 5 – 3 = 2

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В данном случае оно не является уравнением из-за отсутствия переменной. Другое подобное выражение (неверное) также нельзя отнести к числу уравнений: 5+3=2 Уравнениями являются следующие выражения, в состав которых входит переменная х: 5-x=2 5+3x=2

Равенства, в том числе, в составе системы, могут быть справедливыми и неверными. С целью проверки стоит лишь посчитать значения выражений, которые расположены по обе стороны от знака равенства. Когда результаты совпадают, стоит сделать вывод о том, что равенство верно. В случае получения по итогам вычислений разных чисел допустимо заключить, что равенство не является верным.

С другой стороны, уравнение, которое содержит переменные, невозможно так быстро посчитать. Значение частей в уравнении зависит от того, какое значение примет неизвестная и несколько переменных. Путем подстановки численного значения по стандартному алгоритму на место переменной уравнение упрощают. Получив стандартное равенство, его справедливость достаточно просто оценить.

Пример 2

Представим, что имеется некое уравнение: х + 5 = 8

Когда х = 10, выражение примет следующий вид: 10 + 5 = 8

Сделаем вывод о том, что равенство не является верным при таком значении неизвестной. Попробуем подставить в выражение х = 3: 3 + 5 = 8 В результате получилось верное равенство.

Заметим, что существуют некие значения для переменной, при которых равенство становится справедливым. Кроме того, имеются такие значения неизвестной, которые обращают выражение в неверное равенство. Исходя из этой мысли, сформулируем понятие корня уравнения.

Корень уравнения является значением неизвестной, которое обращает рассматриваемое выражение в справедливое числовое равенство.

Решить уравнение — обозначает поиск всех корней рассматриваемого уравнения, либо приведение доказательств об отсутствии таковых корней.

Таким образом, какие-то уравнения несложно решить, а у прочих может не оказаться подходящих к условиям корней. Минимальным уровнем сложности обладают линейные уравнения. Расшифруем этот термин.

Линейное уравнение представляет собой уравнение, которое представлено в следующем виде: ах + b = 0, a и b являются числами, а х играет роль переменной.

Примечание 1

К линейным относят также такие уравнения, которые с помощью метода простых преобразований можно записать в виде ax+b=0.

Пример 3

Запишем линейные уравнения: х + 5 = 18

2х = 8 7 — (х — 3) = х – 6

Нельзя отнести в линейным следующие уравнения:

\({х}^{2} = 0\)

\(\frac{5}{х} = 1\)

\(|х| = 64\)

Простые уравнения с одной переменной.

Все уравнения, которые вы решали в школе, и которые, соответственно, могут встретиться в этом задании ЕГЭ по математике, можно разделить на несколько основных типов — рациональные, иррациональные, показательные, логарифмические, тригонометрические. Точные определения этих терминов вы можете найти в учебнике. Здесь нас будет интересовать только классификация по типам тех уравнений, которые представлены в банке заданий ЕГЭ для задач с кратким ответом. Она нужна для того, чтобы уметь «узнавать уравнение в лицо» и сразу догадываться о том, с чего начинать его решение.

А начинать решение любого уравнения обычно нужно с преобразования его к наиболее простому виду. Наиболее простым, как правило, является такой способ записи уравнения, который совпадает с «Общим видом», представленным в учебнике. Потому что именно для этого способа записи существуют рекомендации по получению ответа. И именно эти рекомендации вы проходили на уроках, именно они изложены в учебниках.

Ниже вы увидите таблицу, которая поможет вам ориентироваться в многообразии уравнений, предлагаемых в этом задании ЕГЭ по математике. В ней символом x обозначена переменная величина, неизвестное значение которой нужно найти. В абсолютном большинстве уравнений используется такое же обозначение. Однако не забывайте, что и другие символы, например y, z, u, v, t, …, имеют право на существование в качестве неизвестных, в том числе, и в уравнениях с одной переменной.
Другими символами в столбце «Общий вид» — a, b, c — обозначены константы, т.е. постоянные для этой записи уравнения величины. Проще говоря, в конкретном случае на их месте просто будут стоять числа.

И, наконец, обозначения со скобками — p(x), q(x), f(x), g(x) — это выражения. На уроках вы не раз должны были слышать термин «математическое выражение». Однако, если это вам всё еще ни о чем не говорит, то называйте его для себя, например, формулой от x.

Первоначально что-то в этой таблице может вам показаться непонятным. Пропустите это и вернитесь к ней еще раз после разбора очередной группы примеров, а также непосредственно перед экзаменом, чтобы быстро повторить все возможные варианты, которые могут встретиться в этом задании.

Внимание: Таблица кликабельна. Если щелкнуть левой клавишей мыши по одному из уравнений в третьем столбце, то загрузится решение этого примера

Но не спешите это делать. Сначала подумайте, как его решите Вы сами. Затем сравните ответы. Ваш способ решения необязательно должен совпадать с моим. Основной критерий правильности — получение тождества при подстановке корня в исходное уравнение.

Тип уравнений	Общий вид	Примеры задач	Признаки
Рациональные	Линейные		В равенстве присутствуют только числа и x в первой степени.
Квадратные		Числа, x и x2. Присутствие x2 обязательно.
Целые рациональные, содержащие многочлен степени n > 2	где p(x) — многочлен		Числа и x в разных степенях. Есть степень, большая, чем 2.
Дробно-рациональные.		Есть х в знаменателе.
Иррациональные	и т.п.		Присутствует знак радикала (знак извлечения корня). x хотя бы один раз встречается под знаком радикала.
Тригонометрические	где |a| ≤ 1, и		х под знаком тригонометрической функции.
Показательные		х находится в показателе степени.
Логарифмические	где a > 0 и a ≠ 1 или и т.п.		х под знаком логарифма или в основании логарифма.
Смешанные			Присутствуют признаки нескольких (чаще двух) типов.

Понятно, что одним примером многообразие задач каждого типа не исчерпывается. Более того, и методов решения уравнений одного типа нужно знать несколько. Посмотрите, например, статьи о квадратных уравнениях.

1. 4,5 способа решения одного квадратного уравнения.
2. Квадратное уравнение. Быстро и без ошибок.

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Решение уравнений методом подбора корня

Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!

Пример. Докажите, что корнями ур-ния

х3 – 2х2 – х + 2 = 0

являются только числа (– 1), 1 и 2.

Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:

(– 1)3 – 2(– 1)2 – (– 1) + 2 = 0

–1 – 2 + 1 + 2 = 0

0 = 0

При х = 1 получаем:

13 – 2•12 – 1 + 2 = 0

1 – 2 – 1 + 2 = 0

0 = 0

Наконец, рассмотрим случай, когда х = 2

23 – 2•22 – 2 + 2 = 0

8 – 8 – 2 + 2 = 0

0 = 0

Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.

Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.

Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

Числа а, а₁, а₂,…а_nи называют коэффициентами уравнений.

Например, для уравнения

5х4 – 7х3 + 9х2 – х + 12 = 0

коэффициенты равны

а = 5

а₁ = – 7

а₂ = 9

а₃ = – 1

а₄ = + 12

Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии

х3 + 2х – 15 = 0

нет слагаемого с буквенной частью х2. Можно считать, что ур-ние равносильно записи

х3 + 0х2 + 2х – 15 = 0

где слагаемое х2 есть, но перед ним стоит ноль. Тогда коэффициент а₁ = 0.

Для обозначения первого коэффициента а может использоваться термин старший коэффициент, а для последнего коэффициента а_n – термин «свободный член» или «свободный коэффициент».

Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:

Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

Тогда можно подставить туда число m и получить верное равенство:

аmn + a₁mn–1 + … + а_n–1m + а_n = 0

Поделим обе его части на m и получим

аmn–1 + a₁mn–2 + … + а_n–1 + а_n/m = 0

Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа аmn–1, a₁mn–2, а_n–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число а_n/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа а_n.

Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.

Пример. Найдите целые корни уравнения

2х4 – х3 – 9х2 + 4х + 4 = 0

Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):

2•14 – 13 – 9•12 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0

2•24 – 23 – 9•22 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0

2•(– 2)4 – (– 2)3 – 9•(– 2)2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0

Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.

Ответ: 1; 2; (– 2).

Пример. Решите ур-ние

0,5х3 + 0,5х + 5 = 0

Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:

0,5х3 + 0,5х + 5 = 0

(0,5х3 + 0,5х + 5)•2 = 0•2

х3 + х + 10 = 0

Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:

(– 2)3 + (– 2) + 10 = – 8 – 2 + 10 = 0

Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х3 и у = х + 10. Значит, и вся левая часть х3 + х + 10 монотонно возрастает

Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.

Ответ: – 2

Ещё быстрее можно узнать, является ли единица корнем уравнения.

Докажем это. Подставим в ур-ние

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

значение х = 1. Так как единица в любой степени равна самой единице, то получим:

а1n + a₁1n–1 + … + а_n–11 + а_n = 0

а + a₁ + … + а_n–1 + а_n = 0

Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.

Пример. Укажите хотя бы 1 корень ур-ния

499х10 – 9990х7 + 501х6 – 10х5 + 10000х4 – 1000 = 0

Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:

499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0

Следовательно, единица является его корнем.

Ответ: 1.

Что такое уравнение?

В общем случае, уравнением называется тождество с одной неизвестной.

Тождеством зовется равенство. То есть уравнение это два равных между собой выражения, одно из которых или оба содержат неизвестное. Важным является условие присутствия только одной неизвестной в одном уравнении.

Можно написать уравнение с двумя и большим количеством переменных, но такое выражение решить не получится. Запомните, даже в системах уравнений, количество переменных должно равняться количеству уравнений. Например, система:

х+3=2

у+х=3

Z+у=4 – имеет решение. А вот уравнение:

Х+у=12 – однозначных решений не имеет. Почему?

Х+3=5

Неизвестная имеет только одно решение. В уравнении х+у=12 – решений бесконечно много. Число х может быть любым, как только мы выберем и подставим любое число, изменится в соответствии с нашим выбором и у. Поэтому и говорят, что у такого уравнения нет определенных решений.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Рациональные уравнения

Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.

Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.

Это интересно!

На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.

Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.

Рациональные уравнения

Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).

Пример:

В данном уравнении ОДЗ Учитывая, что умножим обе части уравнения на

отсюда получим

Подставим полученное значение в уравнение:

Таким образом, является корнем уравнения. Данное уравнение не имеет других корней.

Пример:

Решим уравнение

ОДЗ данного уравнения Умножим обе части уравнения на общий

знаменатель

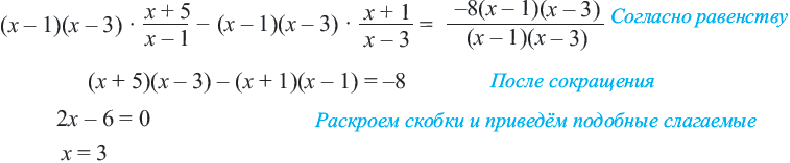
Пример:

В уравнении, ОДЗ

Используя свойство пропорции можно написать:

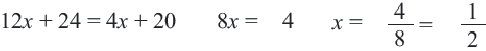
Пример:

Решим уравнение. Здесь ОДЗ,

Умножим обе части уравнения на

Отсюда

Проверьте, являются ли оба этих числа корнями данного уравнения.

Пример:

Решим уравнение

Запишем уравнение в виде и умножим обе стороны на общий множитель Получим

Отсюда

При проверке, убеждаемся что, не удовлетворяет уравнению, т.к. превращает знаменатель в «0». Таким образом, корнем данного уравнения является только

Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней

Решение задач с помощью рациональных уравнений

Задачи на работу

Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за дней, тогда 1-ый рабочий выполнит её за дней

Первый рабочий за 1 день выполняет — ую часть работы, 2-ой — — ую. Вместе, за 1 день они выполнят часть работы. Зная, что вместе за 1 день они выполняют часть работы (согласно условию), составим уравнение Умножим обе части уравнения на Получим, После упрощения имеем Решением данного уравнения являются числа и (не удовлетворяет условию, т.к. ). Итак Ответ: 2-ой рабочий выполняет работу за 20 дней, а 1-ый — за 30 дней.

Задачи на движение

Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.

1-й способ:

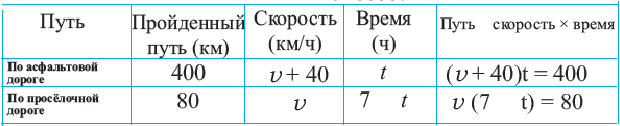Из 2-ой строки таблицы: Из 3-е1 строки таблицы: Отсюда получаем рациональное уравнение

Разделим обе части уравнения на 40:

Получим (противоречит условию задачи)

Ответ: по просёлочной дороге 2 часа

2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом часов, а по проселочной дороге часов.

Зная, что на весь путь он потратил 7 часов, составим уравнение:

Решив данное уравнение, получим = 40 км/ч. Тогда по просёлочной дороге он двигался 80 : 40 = 2 часа.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Рациональные неравенства и их системы
• Геометрические задачи и методы их решения
• Прямые и плоскости в пространстве
• Интеграл и его применение
• Параллельность в пространстве
• Перпендикулярность в пространстве
• Векторы и координаты в пространстве
• Множества

Теорема Виета

Рассмотрим уравнение вида $ax^3+bx^2+cx+d=0$.

Данное уравнение обладает тремя корнями и для того чтобы его решить в общем виде, необходимо решить следующую систему:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

$\begin{cases} x_1 + x_2+x_3=-\frac{b}{a} \\ x_1x_2 + x_2x_3+x_3x_1=\frac{c}{a} \\ x_1x_2x_3=-\frac{d}{a} \\ \end{cases}$

Иначе эти системы уравнений также называют формулами Виета.

Пример 1

Решите уравнение: $x^3+x^2-4x-4=0$.

Решение:

Составим систему уравнений:

$\begin{cases} x_1+ x_2+x_3=-\frac{1}{1} \\ x_1 \cdot x_2 + x_2 \cdot x_3 + x_1 \cdot x_3=-\frac{4}{1}=-4 \\ x_1 \cdot x_2 \cdot x_3= -\frac{4}{1}\\ \end{cases}$

Решив её, получим следующие корни:

$\begin{cases} x_1=-2 \\ x_2=2 \\ x_3=-1 \\ \end{cases}$

Целые рациональные уравнения

Если в уравнении нет переменной \(x\) в знаменателе, то такое уравнение называется целым. Или, другими словами, нигде в уравнении нет деления на переменную.
Метод решения целых рациональных уравнений сильно зависит от того, какой степени перед вами уравнения.

Степень уравнения — это максимальная степень у переменной \(x\).

Например, уравнение \(x^2+5x-1=0\) будет второй степени, так как есть \(x^2\).
Пример уравнения первой степени: \(5x-1=17\);
Уравнение третьей степени: \(5x^3-3x^2=0\);
Уравнение четвертой степени: \(7x^4-5x^2+x-5=0\);
И т.д.

Основной алгоритм решения целых уравнений:

• Если есть скобки, раскрываем их;
• Перекидываем все слагаемые в левую часть так, чтобы в правой части остался только \(0\). Не забываем при этом менять знак этих слагаемых;
• Приводим подобные слагаемые;
• Если получилось уравнение первой степени (в уравнении есть только \(x\)), то решаем его так (линейные уравнения);
• Если получилось уравнение второй степени (в уравнении есть \(x^2\)), то оно решается вот так (квадратные уравнения).
• А вот если в преобразованном уравнении получились члены \(x^3\) или большей степени, то придется применять нестандартные методы решения. Например, замена переменной, группировка, схема Горнера и т.д.

Чаще всего уравнения после преобразований будут сводиться к уравнениям первой (линейные уравнения) и второй (квадратные уравнения) степени.

Разберем примеры целых рациональных уравнений:

Пример 1
$$-4(-7+6x)=-9x-5;$$
Первым делом раскрываем скобки:
$$28-24x=-9x-5;$$
Перекидываем все слагаемые из правой части в левую:
$$28-24x+9x+5=0;$$
Поменяем слагаемые местами, чтобы удобнее было приводить подобные слагаемые:
$$-24x+9x+5+28=0;$$
$$-15x+33=0;$$
Получили линейное уравнение. Чтобы его решить, перекидываем свободный член (тот, что без \(x\)) в правую часть:
$$-15x=-33;$$
И поделим уравнение слева и справа на \(-15\):
$$x=\frac{-33}{-15};$$
$$x=\frac{11}{5}=2,2;$$
Ответ: \(x=2,2.\)

Важно отметить, то, что уравнение линейное, стало видно сразу после раскрытия скобок: у нас же не было степени у \(x\)-ов. Поэтому разумно было сразу решать его как линейное: перенести все слагаемые с \(x\) в левую часть, а все числа в правую

Так бы получилось немного короче.

Пример 2
$$4*(x+1)^2-2(x+3)=(2x-5)^2;$$
Тут сразу и не скажешь, какой степени уравнение. На первый взгляд кажется, что квадратное, но давайте раскроем скобки, воспользовавшись формулами сокращенного умножения:
$$4*(x^2+2x+1)-2x-6=4x^2-20x+25;$$
$$4*x^2+8x+4-2x-6=4x^2-20x+25;$$
Перекинем все в левую часть, не забывая поменять знак:
$$4*x^2+8x+4-2x-6-4x^2+20x-25=0;$$
Поменяем местами слагаемые, чтобы было проще приводить подобные:
$$4x^2-4x^2+8x-2x+20x+4-6-25=0;$$
$$26x-27=0;$$
Как видите, все квадраты сократились, и уравнение превратилось в линейное:
$$26x=27;$$
$$x=\frac{27}{26};$$
Ответ: \(x=\frac{27}{26}.\)

Пример 3
$$\frac{x}{6}+\frac{x}{12}+x=-\frac{35}{4};$$
Домножим уравнение слева и справа на \(12\). Почему именно на \(12\)? Потому что в уравнении есть дроби с знаменателями \(6\), \(12\) и \(4\), на все эти числа \(12\) можно разделить:
$$12*(\frac{x}{6}+\frac{x}{12}+x)=12*(-\frac{35}{4});$$
$$12*\frac{x}{6}+12*\frac{x}{12}+12*x=12*(-\frac{35}{4});$$
$$2x+x+12x=-3*35;$$
$$15x=-105;$$
$$x=\frac{-105}{15}=-7;$$
Ответ: \(x=-7.\)

Подробнее про линейные уравнения можно почитать в отдельной статье.

Пример 4
$$(x-1)^2=2x^2-6x-31;$$
Раскроем скобки:
$$x^2-2x+1=2x^2-6x-31;$$
$$x^2-2x+1-2x^2+6x+31=0;$$
$$x^2-2x^2-2x+6x+1+31=0;$$
$$-x^2+4x+32=0;$$
После приведения подобных слагаемых в уравнении остался \(x^2\), а значит перед нами квадратное уравнение, которое можно решить через дискриминант:
$$a=-1; \quad b=4; \quad c=32;$$
$$D=b^2-4ac=4^2-4*(-1)*32=16+128=144=12^2;$$
$$x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-4+12}{2*(-1)}=\frac{8}{-2}=-4;$$
$$x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-4-12}{2*(-1)}=\frac{-16}{-2}=8;$$
Ответ: \(x=-4; \qquad x=8.\)