Тригонометрические уравнения

Введение вспомогательного угла

В правой части однородного ур-ния стоит ноль. Усложним задачу и рассмотрим схожие ур-ния, у которых справа стоит произвольное число, которое может быть и отлично от нуля. То есть ур-ние имеет вид

Существует ли универсальный метод решения тригонометрических уравнений такого вида? Да, существует, и называется он методом вспомогательного угла. Очевидно, что величина a 2 + b 2 является положительной, ведь это сумма квадратов чисел, отличных от нуля. Это значит, что существует действительное число

которое больше нуля.

Поделим ур-ние на N и получим новое ур-ние

Для краткости введем новые обозначения:

коэффициенты уравнения запишем большими буквами, чтобы не писать корни.

и тогда ур-ние примет более простой вид:

Попытаемся найти величину А 2 + В 2 :

Так как величина А 2 + В 2 равна единице, то можно подобрать такой угол α, что будут одновременно выполняться равенства

Угол α называют вспомогательным углом. Как его подобрать? Из равенства А = sinα очевидно, что

Заменим в (1) числа А и В по формулам (2) и (3) и получим:

Теперь слева стоит косинус разности, который можно «свернуть»:

Это уже почти что простейшее тригонометрическое уравнение, которое мы сможем решить.

Задание. Решите ур-ние

Решение. Коэффициенты перед синусом и косинусом равны 5 и 12. Найдем корень из суммы 5 2 + 12 2 :

Значит, число N = 13. Поделим ур-ние на 13:

Теперь введем вспомогательный угол α = arcsin 5/13. Тогда

Подставим в (1) вместо дробей 5/13 и 12/13 sinα и cosα:

Теперь смотрим в тригонометрические формулы сложения и вычитания аргументов. Есть ли там что-то похожее на левую часть ур-ния? Действительно, там есть следующая формула:

Наше ур-ние похоже на эту формулу, но надо поменять местами вычитаемое и уменьшаемое. Для этого можно умножить ур-ние на (– 1):

Видео:Тригонометрические уравнения которые сводятся к алгебраическим. Метод: замены переменных.Скачать

Что такое уравнение? Смысл и понятия.

Узнаем сначала все понятия, связанные с уравнением.

Определение:Уравнение – это равенство, содержащее переменные и числовые значения.

Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.

Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.

Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.

Рассмотрим теперь, все термины на простом примере:
x+1=3

В данном случае x – переменная или неизвестное значение уравнения.

Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.

2+1=3

Получили верное равенство. Значит, правильно нашли корни уравнения.

Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.

Здравствуйте!

Мы вплотную подошли к решению задачи № 13 варианта КИМ ЕГЭ. Постараемся, чтобы результаты наших занятий на этой неделе обеспечили вам один первичный балл за задачу №13 — вспомним и применим на практике основные методы решения тригонометрических уравнений.

1. Сведение к квадратному уравнению

Начнем мы с самого простого метода, когда тригонометрическое уравнение с помощью замены переменных сводится к квадратному (в общем случае — рациональному) уравнению. Но и здесь есть свои особенности и подводные камни. Посмотрим, как их избежать.

2. Разложение на множители

Нередко при решении тригонометрических уравнений используется такой прием, как разложение на множители. Здесь можно использовать и группировку, и вынесение общего множителя за скобку, и применять формулы сокращенного умножения к формулам тригонометрии.

3. Однородные тригонометрические уравнения

Очень важный тип тригонометрических уравнений — однородные. Что это за уравнения и как их решать, смотрите в видеолекции.

Попробуйте свои силы в применении основных методов решения тригонометрических уравнений для решения задач, которые могут встретиться вам на экзамене.
Для решения этих уравнений вам понадобятся которые мы рассмотрели выше. Ответы, как обычно, под спойлерами.

Условие	Ответ
Сведение к квадратному
Решить уравнение 2sin2x+7sinx=4
Решить уравнение 3cosx+3=4sin2x
Решить уравнение 2sin2x+ctgx=2.
Разложение на множители
Решить уравнение 2sin2x+5sin2x=
Решить уравнение cosx+cos5x-2cos3x=
Решить уравнение 2sin2x+ctgx=2.
Однородные уравнения
Решить уравнение 3cos2x+4sin2x=
Решить уравнение -sinx+7cosx3cosx-8sinx=83
Решить уравнение sin2x+3sin2x-7cos2x=
Решить уравнение 17sin2x-37sinxcos2x+6cos22x=

Для «продвинутых» слушателей нашего курса мы предлагаем еще несколько методов решения тригонометрических уравнений.

Уравнения с тангенсами и котангенсами

В уравнениях с тангенсами и котангенсами появляется область допустимых значений аргумента, которая влияет на отбор корней: для тангенса cos(x) ≠ 0, т.е. x ≠ πn/2, для котангенса sin(x) ≠ 0, т.е. x ≠ πn

Использование формул преобразования произведения в сумму и суммы в произведение

И несколько задач посложнее, для тех, кто не ограничился тремя основными методами, а захотел узнать больше.

Условие	Ответ
Уравнения вида fsin⁡x±cos⁡x;sin⁡x⋅cos⁡x=
Решить уравнение 1-sinx+cosx=13sin2x
Решить уравнение sinx+cosx=sinx-cosx2
Решить уравнение 4sin3x+cos3x=11sinx+cosx2
Метод введения вспомогательного аргумента
Решить уравнение sinx+3cosx=3
Решить уравнение 3sinx-4cosx=5
Решить уравнение sinxcosx+cos2x=1,2
Универсальная тригонометрическая подстановка
Решить уравнение 2tg⁡x2+sinx+5cos⁡x+3=
Решить уравнение tg⁡x2+1=2sinx+cos⁡x
Решить уравнение 3sinx+41+cos⁡x+3tg⁡x=

Если вам не удалось решить все уравнения — не беда. Попробуйте еще раз, но уже с подсказками пошагового тренажера. Тренажер проведет вас по шагам решения, подскажет, что нужно сделать, проверит промежуточные вычисления и окончательный ответ.

Перейти в БиблиотекуВыбрать вариант подписки

Нам осталось рассмотреть последний и очень важный для решения задачи №13 вопрос — какие бывают условия для отбора корней тригонометрического уравнения и как выбрать подходящий для конкретного условия способ отбора. Это тема наших занятий на следующей неделе.

Календарь занятий
Тема недели

Замена переменной в тригонометрических уравнениях

Замена выражения под тригонометрической функцией

Мы научились решать простейшие уравнения. И на этом строится решение всех остальных тригонометрических уравнений. Они все так или иначе сводятся к решению простейших. И один из способов – это введение замены переменной.

Вы должны были с этим регулярно сталкиваться в младших классах при решении, например, биквадратных уравнений. Все дальнейшие рассуждения предполагают, что вы знаете, что такое замена переменной. Итак, разберем пример:

Пример 18
$$\sin(2x)=\frac{\sqrt{3}}{2};$$

Обратите внимание, что теперь у нас под синусом стоит не просто \(x\), а целое выражение. Давайте избавимся от него, убрав \(2x\) в замену: пусть \(t=2x\)

Теперь наше уравнение превратилось в простейшее тригонометрическое. Решаем его относительно переменной \(t\) (вы можете решать при помощи единичной окружности или по готовым формулам, как вам удобнее. Я же буду просто выписывать ответ):
$$t_{1}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$t_{2}=\frac{2\pi}{3}+2\pi*n, \quad n \in Z;$$

На этом решение не заканчивается. Мы нашли значения \(t\), а нам надо найти \(x\). Делаем обратную замену, вспоминая, что \(t=2x\):
$$2x_{1}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$2x_{2}=\frac{2\pi}{3}+2\pi*n, \quad n \in Z;$$
И просто выражаем из получившихся выражений \(x\), для этого разделим левую и правую часть равенства на \(2\):
$$\frac{2x_{1}}{2}=\frac{\frac{\pi}{3}+2\pi*n}{2}, \quad n \in Z;$$
$$\frac{2x_{2}}{2}=\frac{\frac{2\pi}{3}+2\pi*n}{2}, \quad n \in Z;$$

$$x_{1}=\frac{1}{2}*\frac{\pi}{3}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{1}{2}*\frac{2\pi}{3}+\pi*n, \quad n \in Z;$$
Обратите внимание, что период тоже не забываем поделить на \(2\). Ответ:
$$x_{1}=\frac{\pi}{6}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+\pi*n, \quad n \in Z.$$

Ответ:
$$x_{1}=\frac{\pi}{6}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+\pi*n, \quad n \in Z.$$

Аналогичным образом можно решать тригонометрические уравнения с более сложным подтригонометрическим выражением:

Пример 19
$$tg(\frac{2x+\pi}{3})=1;$$

Под тангенсом тут стоит целая дробь, зависящая от \(x\). Засунем всю эту дробь в замену:
$$t=\frac{2x+\pi}{3};$$
Уравнение примет вид:
$$tg(t)=1;$$
Решением этого простейшего уравнения будет:
$$t=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
Делаем обратную замену, вместо \(t\) подставляем \(\frac{2x+\pi}{3}\):
$$\frac{2x+\pi}{3}=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
И выражаем отсюда \(x\). Домножим равенство на \(3\):
$$2x+\pi=3*(\frac{\pi}{4}+\pi*n), \quad n \in Z;$$
$$2x+\pi=\frac{3\pi}{4}+3\pi*n, \quad n \in Z;$$
Перенесем \(\pi\) направо:
$$2x=-\pi+\frac{3\pi}{4}+3\pi*n, \quad n \in Z;$$
Приведем подобные слагаемые:
$$2x=-\frac{\pi}{4}+3\pi*n, \quad n \in Z;$$
И разделим на \(2\):
$$x=-\frac{\pi}{8}+\frac{3}{2}*\pi*n, \quad n \in Z;$$

Ответ:
$$x=-\frac{\pi}{8}+\frac{3}{2}*\pi*n, \quad n \in Z;$$

Замена всей тригонометрической функции

Что делать с подтригонометрическим выражением, мы разобрались. Теперь решим пример на замену, при помощи которой тригонометрическое уравнение сводится к квадратному.

Пример 20
$$2*\sin^2(x)+\sin(x)-1=0;$$
Обращаем внимание на одинаковое выражение \(\sin(x)\). Сделаем замену:
$$t=\sin(x);$$
$$2t^2+t-1=0;$$
Получили обыкновенное квадратное уравнение, которое решается через дискриминант:
$$D=1-4*2*(-1)=9;$$
$$t_{1}=\frac{-1+3}{4}=\frac{1}{2};$$
$$t_{2}=\frac{-1-3}{4}=-1;$$
Делаем обратную замену и получаем два простейших тригонометрических уравнения

Первое:
$$\sin(x)=\frac{1}{2};$$
$$x_{1}=\frac{\pi}{6}+2\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{5\pi}{6}+2\pi*n, \quad n \in Z;$$
Второе:
$$\sin(x)=-1;$$
$$x_{3}=\frac{3\pi}{2}+2\pi*n, \quad n \in Z;$$
Записываем ответ из трех наборов решений.

Полезен ли упроститель уравнений?

Абсолютно! Упрощение уравнения перед его решением может оказаться одним из наиболее практичных действий. Одно, казалось бы, сложное уравнение можно свести к чему-то гораздо более простому после некоторых базовых упрощений.

Используйте это

калькулятор упрощения

взять любое выражение и упростить его до простейшего выражения.

Пример. решите следующее линейное уравнение

Решите следующее линейное уравнение относительно x и y: \(\frac{1}{3} x + \frac{5}{4} y = \frac{5}{6}\)

Отвечать:

В данном случае у нас есть линейное уравнение относительно x и y, поэтому нам нужно выбрать одну переменную для решения. Давайте решим за y:

Упрощение коэффициента приводит к:

чем завершается расчет.

Пример: решения полиномиального уравнения

Найдите решения следующего уравнения: \(2x^2 + x y + y^2 = 1\).

Отвечать:

Нам необходимо решить следующее заданное полиномиальное уравнение:

В уравнении есть две переменные: \(y\) и \(y\), поэтому целью в данном случае является нахождение \(y\) в терминах \(y\).

\( \displaystyle 2x^2+xy+y^2=1\)

This corresponds to a quadratic equation in y

\( \displaystyle \,\,\)

\(\displaystyle 2x^2+xy+y^2-1=0\)

By solving this quadratic equation on y, we obtain

\( \displaystyle \,\,\)

\(\displaystyle y = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}\)

and putting in the coefficients \(a = 1\), \(b = x\) and \(c = 2x^2-1\)

\( \displaystyle \,\,\)

\(\displaystyle y = \frac{-\left( x \right) \pm \sqrt{\left( x \right)^2 — 4\left( 1 \right)\left( 2x^2-1 \right)}}{2\left( 1 \right)}\)

from which we obtain

\( \displaystyle \,\,\)

\(\displaystyle y=-\frac{1}{2}x-\frac{1}{2}\sqrt{-7x^2+4}, \,\,y=-\frac{1}{2}x+\frac{1}{2}\sqrt{-7x^2+4}\)

Из приведенного выше полиномиального уравнения находим следующее решение:

Следовательно, решение \(y\) для данного уравнения приводит к решениям \(y=-\frac{1}{2}x-\frac{1}{2}\sqrt{-7x^2+4},\,\,y=-\frac{1}{2}x+\frac{1}{2}\sqrt{-7x^2+4}\).

Пример: поиск решений тригонометрических уравнений

Сколько решений (если таковые имеются) имеет следующее тригонометрическое уравнение: \( \sin(x) = 0 \).

Отвечать

: Нам необходимо решить следующее заданное тригонометрическое уравнение:

Уравнение, которое нам нужно решить, имеет только одну переменную — \(x\), поэтому цель состоит в том, чтобы решить ее.

Решение этого тригонометрического уравнения

\( \displaystyle \sin\left(x\right)=0\)

We need to apply the inverse trigonometric function \(\arcsin(\cdot)\), so we find that

\( \displaystyle \,\,\)

\(\displaystyle \arcsin\left(\sin\left(x\right)\right)=\arcsin\left(0\right)\)

so then we find that

\( \displaystyle \,\,\)

\(\displaystyle x =\arcsin\left(0\right)=0\)

Используя свойства обратной тригонометрической функции \( \arcsin(\cdot)\), а также свойства тригонометрической функции \( \sin\left(x\right)\), находим, что

Следовательно, решение \(x\) для данного уравнения приводит к решению \(x=\pi{}K\) для произвольной целочисленной константы \(K\). Следовательно, исходное уравнение имеет бесконечные решения.

Уравнения с ограничениями на значение переменной

До этого мы рассматривали случаи, при которых переменная х могла принимать любые значения в уравнении. Однако, если в ур-нии переменная стоит под знаком корня или находится в знаменателе, то возникают некоторые ограничения на те значения, которые она может принимать. Рассмотрим пример.

Задание. Решите ур-ние

Решение. В левой части произведение двух множителей, а справа – ноль, следовательно, можно записать:

Решение для первого уравнения запишем в виде двух серий, а не одной (так проще будет проводить дальнейшее исследование). Сначала вычислим арксинус:

Тогда получаем три серии решений:

Теперь учтем, что в исходном уравнении выражение cosx стоит под корнем, поэтому должно соблюдаться условие:

Косинус принимает положительные значения в I и IV четверти. Отметим все серии решении на единичной окружности и посмотрим, какие из них попадают в I и IV четверть:

Теперь мы видим, что корни из серии 4π/3 + 2πn находятся в III четверти, то есть для них соsx 2 x = ctgx

Видео:Как решать тригонометрические уравнения методом замены переменной. Тригонометрия 10. Видеоурок #44Скачать

Подробнее об этом калькуляторе уравнений

Этот калькулятор позволит вам

решать уравнения

в общем, показаны все соответствующие шаги. Сначала вам нужно указать уравнение, которое вы хотите решить. Например, вы можете захотеть

решить это квадратное уравнение

\(x^2 + 3x+2 = 0\).

Или, возможно, вы хотите решить тригонометрическое уравнение \(\sin(x) = 0\).

Это примеры уравнений с одной переменной. Возможно, вам захочется решить уравнения с несколькими переменными. Например, вы можете решить \(x^2 + x y +y^2 = 1\) — уравнение с двумя переменными x и y. В этом случае калькулятор попытается найти решение для y (или решить для x, как будет проще)

После того как вы предоставите действительное уравнение, все, что вам нужно сделать, это нажать кнопку «Решить», и вам будут предоставлены все этапы вычислений, окончательное решение, если таковое имеется, или вывод о том, что никакие решения не могут быть найдены. быть найденным.

Смогу ли я решить все уравнения?

Нет. Решение алгебраических уравнений, которые не являются линейными или полиномиальными, в целом является сложной задачей, и не существует универсальной формулы или даже универсального подхода, который позволил бы решить все уравнения.

И это верно для уравнений с одной переменной, и еще более верно для уравнений с большим количеством переменных.

Хотя решать уравнения в целом сложно, большинство уравнений, возникающих из задач алгебры, относительно просты и сводятся к основным линейным или квадратным уравнениям, а также к некоторым элементарным тригонометрическим уравнениям.

Однородные уравнения

Рассмотрим уравнение: sin2x+2sinxcosx-3cos2=0.

Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене a2+2ab-3b2степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).

Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Запомни: Предположим, что cosx=0. Тогда в силу уравнения и sinx=0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx, и мы можем поделить обе его части на cos2x.

В результате деления приходим к равносильному квадратному уравнению относительно тангенса:

tg2x+2tgx-3=0

Это были основные три метода решения тригонометрических уравнений. Именно они обычно применяются в 12 задании ЕГЭ. Так что больше тренируйся и делай домашние задания!

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Рассмотрим следующий пример:
Найдите корни уравнения   .

Решение:
Так как перед переменной x стоит коэффициент  необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

1x=21 или x=21

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а   в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте  перед переменной x убрать из знаменателя 5.

3x=45

Далее делим все уравнение на 3.

3x:3=45:3
(3:3)x=15

1x=15 или x=15

Сделаем проверку. Подставим в уравнение найденный корень.

5=5

Ответ: x=15

Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы ,  и , причем последняя формула чаще используется в обратном направлении: .

Пример 7

Найти неопределенный интеграл.

Решение:

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу  (понизив степень подынтегральной функции)

Обратите внимание, что я сократил решение. По мере накопления опыта интеграл от  можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий

В данном случае целесообразно не расписывать и правило , сначала устно берем интеграл от 1, затем – от .

Пример 8

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Таки обещанное повышение степени:

Пример 9

Найти неопределенный интеграл.

Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы .

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.

(4) Используем формулу

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы .

(6) Приводим подобные слагаемые (здесь я почленно разделил  и выполнил сложение ).

(7) Собственно берём интеграл, правило линейности  и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

! В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ  можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

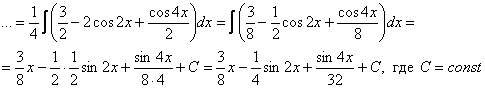
Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:

Пример 10

Найти неопределенный интеграл.

Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

Подытоживая параграф, сделаем вывод: любой интеграл вида , где  и  – чётные числа, решается методом понижения степени подынтегральной функции.
На практике мне встречались интегралы с 8 и 10 степенями, решать их ужасный гемор приходилось, понижая степень несколько раз, в результате чего получались длинные-длинные ответы.

В каких случаях необходимо решать уравнения

Решение уравнений необходимо во множестве различных ситуаций и областей человеческой деятельности.

• Научные и инженерные исследования: В науке и инженерии уравнения используются для моделирования физических явлений и процессов. Решение уравнений позволяет ученым и инженерам предсказывать поведение систем, проводить анализ данных и разрабатывать новые технологии.
• Финансовые расчеты: Уравнения используются для решения финансовых задач, таких как расчет процентов, определение стоимости инвестиций, оценка рисков и т. д. Решение уравнений помогает финансистам и экономистам принимать обоснованные решения в сфере финансов.
• Промышленность и производство: В промышленности уравнения используются для оптимизации производственных процессов, расчета рабочих нагрузок, управления запасами и других аспектов управления производством.
• Технические расчеты: Уравнения применяются в различных технических областях, таких как строительство, авиация, автомобилестроение и т. д. Они используются для проектирования конструкций, оптимизации дизайна и тестирования материалов.
• Медицинские и биологические исследования: Уравнения используются для моделирования биологических процессов, расчета фармакокинетики и фармакодинамики лекарственных препаратов, анализа медицинских данных и т. д.
• Компьютерное моделирование: Уравнения применяются в компьютерном моделировании для создания виртуальных сред, анализа сложных систем и разработки программных продуктов.
• Повседневные задачи: Уравнения могут использоваться в повседневной жизни для решения различных практических задач, таких как расчеты по планированию бюджета, определение расстояний и скоростей при движении, решение геометрических задач и т. д.

В целом, решение уравнений является важным инструментом для анализа, прогнозирования и оптимизации различных процессов и явлений в различных областях знаний и человеческой деятельности.

Формулы двойных углов

Как еще мы можем поколдовать с аргументом? Разобрать двойной угол. 

Из самого названия следует, что аргумент функции будет умножен на 2. Например, \(cos(2x)\). 

Но математики уже позаботились о нас, и чтобы мы не мучились, вывели формулы, по которым просто преобразовать двойной угол и перейти к обычному аргументу. Рассмотрим их. 

\(sin(2x)=2sin x*cos x\)\(cos(2x)=cos^2x-sin^2x\)\(tg(2x)=\frac{2tg x}{1-tg^2x}\)\(ctg(2x)=\frac{ctg^2x-1}{2ctg x}\)

Заметили, что косинус выделился и тут? На самом деле, у него целых три формулы для двойного угла. Попробуем вывести еще две. Для этого вернемся к основному тригонометрическому тождеству и выразим квадрат косинуса:

\(sin^2x+cos^2x=1 =>cos^2x=1-sin^2x\)

Теперь подставим полученное выражение в формулу косинуса двойного угла:

\(cos(2x)=cos^2x-sin^2x=(1-sin^2x)-sin^2x=1-2sin^2x\)

Аналогичным способом выведем формулу двойного угла только через косинусы:

\(sin^2x+cos^2x=1 =>sin^2x=1-cos^2x\)\(cos(2x)=cos^2x-sin^2x=cos^2x-(1-cos^2x)=cos^2x-1+cos^2x=2cos^2x-1\)

Таким образом, мы получили еще две формулы для двойного угла.

\(cos(2x)=1-2sin^2x\)\(cos(2x)=2cos^2x-1\)

Важно заметить, что формулы работают в обе стороны. Читать их можно как слева направо, так и справа налево

Преобразование тригонометрических выражений встречается в №6 ЕГЭ по профильной математике. Найдите значение выражения \(11\sqrt{3}-22\sqrt{3}*sin^2(\frac{\pi}{12})\)Решение.Заметим, что у нас есть общий множитель \(11\sqrt3\). Вынесем его за скобки:\(11\sqrt{3}*1-2*11\sqrt{3}*sin^2(\frac{\pi}{12}))=11\sqrt{3}(1-2sin^2(\frac{\pi}{12}))\)В скобке у нас получилось формула косинуса двойного угла. «Свернем» ее:\(11\sqrt3*cos(2*\frac{\pi}{12})=11\sqrt3*cos(\frac{\pi}{6})\)У нас получилось табличное значение косинуса. Подставляем его и считаем ответ:\(11\sqrt3*\frac{\sqrt3}{2}=\frac{11*3}{2}=16,5\)Ответ: \(16,5\)

Теперь попробуем еще сильнее усложнить аргумент. Пусть вместо него будет стоять алгебраическое выражение. 

Простейшие тригонометрические уравнения

Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.

Уравнение `sin x=a`.

При `|a|>1` не имеет решений.

При `|a| leq 1` имеет бесконечное число решений.

Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`

Таблица арксинусов

Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| leq 1` имеет бесконечное множество решений.

Формула корней: `x=pm arccos a + 2pi n, n in Z`

Таблица арккосинусов

Частные случаи для синуса и косинуса в графиках.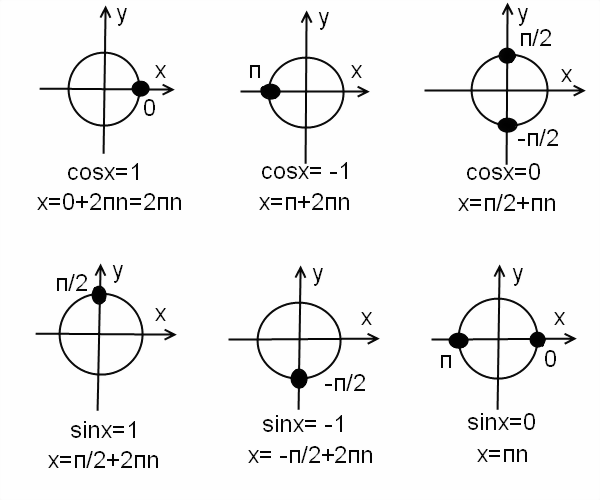

Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + pi n, n in Z`

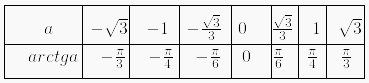
Таблица арктангенсов

Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + pi n, n in Z`

Таблица арккотангенсов

Основные методы решения уравнений

Ключевые слова: решение уравнения, тождественное преобразование, тождественные преобразования, посторонний корень, потеря корня.

Решение уравнения
– это процесс, состоящий в основном в замене заданного уравнения другим
уравнением, ему равносильным.
Такая замена называется
тождественным преобразованием.

Основные тождественные преобразования:

Замена одного выражения другим,
тождественно равным ему.
Например,
уравнение( 3x+
2 ) 2 = 15x+10 можно
заменить следующим равносильным:9×2 +
12x + 4 = 15x + 10

Перенос членов уравнения из
одной стороны в другую с обратными знаками.Так, в предыдущем
уравнении мы можем перенести все его члены из правой
части в левую со знаком « – »: 9×2 +
12x + 4 – 15x – 10 = 0, после чего получим:
9×2 –
3x – 6 = 0 .
Умножение или деление обеих
частей уравнения на одно и то же выражение (число), отличное от нуля

Это очень важно, так какновое уравнение может не
быть равносильным предыдущему, если выражение, на которое мы умножаем или
делим, может быть равно нулю. Уравнение x
– 1 = 0 имеет
единственный корень x
= 1

Умножив обе
его части на x
– 3 , мы получим
уравнение ( x
– 1 )( x
– 3 ) = 0, у которого
два корня: x
= 1 и x = 3. Последнее значение не является корнем заданного уравнения x
– 1 = 0. Это так
называемый посторонний корень. И наоборот,
деление может привести к потере корня. Так, если ( x
– 1)(x
– 3) = 0 является исходным уравнением,
то корень x
= 3 будет потерян при
делении обеих частей уравнения на x
– 3 .

Можно возвести обе части
уравнения в нечетную степень или извлечь из обеих
частей уравнения корень нечетной степени.Необходимо помнить, что: а) возведение в четную
степень может привести к приобретениюпосторонних корней; б) неправильное
извлечение корня четной степени может привестик
потере корней.

Уравнение 7x
= 35 имеет
единственный корень x
= 5 . Возведя обе части
этого уравнения в квадрат, получим уравнение: 49×2= 1225 ,имеющее
два корня: x = 5иx = – 5. Последнее значение является посторонним корнем. Неправильное извлечение квадратного корня из обеихчастей
уравнения 49x 2= 1225 даёт в
результате 7x = 35,и мы
теряем корень x = – 5. Правильное
извлечение квадратного корня приводит куравнению: | 7x | = 35, а
следовательно, к двум случаям: 1) 7x = 35, тогда x = 5 ; 2) –
7x = 35, тогда x = – 5 .Следовательно, при правильном извлечении квадратного корня
мы не теряем корней уравнения.

ОДЗ

(областью допустимых значений) уравнения называется множество тех значений неизвестной, при которых определены его правая и левая части.

Пример. Решите уравнение $$\sqrt{x^{2}-x} + \sqrt{2 — x — x^{2}} = \sqrt{x} — 1$$

Решение. В этом примере наоборот сложно его решение. Однако поиск ОДЗ приносит несомненную пользу.
В самом деле, ОДЗ: $$\left\{ \begin{array}{l}
x^2 — x \ge 0 \\ 2 — x — x^2 \ge 0 \\ x \ge 0 \end{array} \right.\, \Leftrightarrow \left\{ \begin{array}{l} x \in \left( { — \infty ;0} \right] \cup \left \\ x \in \left[ {0; + \infty } \right) \end{array} \right.\, \Leftrightarrow \left[ \begin{array}{l} x = 0 \\ x = 1 \end{array} \right.$$

Значит, ОДЗ нашего уравнения содержит только два числа. А поскольку вне
ОДЗ решений быть не может, то корнями нашего уравнения могут быть
только эти два числа. Для того чтобы понять, какое из них действительно
является решением, нужно полученные числа подставить в уравнение.
Подстановка даёт, что
x
= 0 не является решением уравнения, а

x
= 1 − является.

Ответ.
1.

Таким образом, к понятию ОДЗ нужно относиться творчески и искать его,
только если в этом возникает существенная необходимость. Так, например,
в равносильном переходе $$\sqrt {f(x)} = g(x)\, \Leftrightarrow \left\{ \begin{array}{l} g(x) \ge 0, \\ f(x) = g^2 (x) \end{array} \right.$$

требование

g
(x) ? 0 задает ОДЗ. Однако, если искать

g (x) очень сложно, то проще подставить найденные корни в исходное уравнение, чем выяснять, при каких

x
выполнено неравенство

g (x) ? 0.

Метод замены переменной

Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция  и её производная : (функции ,  не обязательно находятся в произведении)

Пример 11

Найти неопределенный интеграл.

Смотрим в таблицу производных и замечаем формулы , , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же  обозначать за  – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.

Общий ориентир: в похожих случаях за  нужно обозначить функцию, которая находится в знаменателе.

Прерываем решение и проводим замену

В знаменателе у нас всё хорошо, всё зависит только от , теперь осталось выяснить, во что превратится .
Для этого находим дифференциал :

Или, если короче:
Из полученного равенства по правилу пропорции выражаем нужное нам выражение:

Итак:
Теперь всё подынтегральное выражение у нас зависит только от  и можно продолжать решение

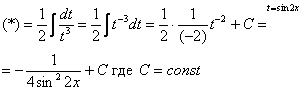
Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.

Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.

 А сейчас два примера для самостоятельного решения:

Пример 12

Найти неопределенный интеграл.

Пример 13

Найти неопределенный интеграл.

Полные решения и ответы в конце урока.

Пример 14

Найти неопределенный интеграл.

Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за , синус или косинус?

Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за  другую функцию, но есть:

Общий ориентир: за  нужно обозначить ту функцию, которая, образно говоря, находится в «неудобном положении».

Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе. 

Поэтому проведем замену:

Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала , то следует вернуться к уроку Метод замены переменной в неопределенном интеграле.

Пример 15

Найти неопределенный интеграл.

Анализируем подынтегральную функцию, что нужно обозначить за ?
Вспоминаем наши ориентиры:
1) Функция, скорее всего, находится в знаменателе;
2) Функция находится в «неудобном положении».

Кстати, эти ориентиры справедливы не только для тригонометрических функций.

Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена . В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с ? Во-первых, «отщипываем» один косинус:

 мы резервируем под наш «будущий» дифференциал

А  выражаем через синус с помощью основного тригонометрического тождества:

Вот теперь замена:

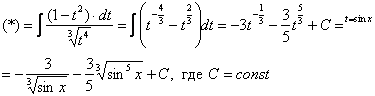
Готово.

Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за  – обозначить другую функцию. Речь идет только об интегралах, где есть косинусы и синусы.

В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за  обозначили синус.

Пример 16

Найти неопределенный интеграл.

Степени идут на взлёт =).
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.