Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но, на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого, тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Формулы двойного угла
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол \(2\alpha\) через \(\alpha\). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$\cos(2\alpha)=\cos(\alpha+\alpha)=\cos(\alpha)*\cos(\alpha)-\sin(\alpha)*\sin(\alpha)=\cos^2(\alpha)-\sin^2(\alpha);$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$\cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)=1-\sin^2(\alpha)-\sin^2(\alpha)=1-2\sin^2(\alpha);$$
$$\cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)=\cos^2(\alpha)-(1-\cos^2(\alpha))=2\cos^2(\alpha)-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$\sin(2\alpha)=\sin(\alpha)*\cos(\alpha)+\sin(\alpha)*\cos(\alpha)=2\sin(\alpha)\cos(\alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2\alpha)=\frac{\sin(2\alpha)}{\cos(2\alpha)}=\frac{2\sin(\alpha)\cos(\alpha)}{\cos^2(\alpha)-\sin^2(\alpha)}=\frac{\frac{2\sin(\alpha)\cos(\alpha)}{\cos^2(\alpha)}}{\frac{\cos^2(\alpha)-\sin^2(\alpha)}{\cos^2(\alpha)}}=\frac{\frac{2\sin(\alpha)}{\cos(\alpha)}}{1-\frac{\sin^2(\alpha)}{\cos^2(\alpha)}}=\frac{2tg(\alpha)}{1-tg^2(\alpha)};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2\alpha)=\frac{\cos(2\alpha)}{\sin(2\alpha)}=\frac{\cos^2(\alpha)-\sin^2(\alpha)}{2\sin(\alpha)\cos(\alpha)}=\frac{\frac{\cos^2(\alpha)-\sin^2(\alpha)}{\sin^2(\alpha)}}{\frac{2\sin(\alpha)\cos(\alpha)}{\sin^2(\alpha)}}=\frac{\frac{\cos^2(\alpha)}{\sin^2(\alpha)}-1}{\frac{2\cos(\alpha)}{\sin(\alpha)}}=\frac{ctg^2(\alpha)-1}{2ctg(\alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение \(24\cos(2\alpha)=?\), если \(\sin(\alpha)=-0,2.\)
Воспользуемся формулой косинуса двойного угла:
$$\cos(2\alpha)=1-2\sin^2(\alpha);$$
$$24\cos(2\alpha)=24(1-2\sin^2(\alpha))=24-48\sin^2(\alpha)=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение \(\frac{10\sin(6\alpha)}{3\cos(3\alpha)}=?\), если \(\sin(3\alpha)=0,6.\)
Используем синус двойного угла, для этого представим \(6\alpha=2*(3\alpha)\):
$$\sin(6\alpha)=\sin(2*(3\alpha))=2\sin(3\alpha)\cos(3\alpha);$$
$$\frac{10\sin(6\alpha)}{3\cos(3\alpha)}=\frac{10*2\sin(3\alpha)\cos(3\alpha)}{3\cos(3\alpha)}=\frac{20\sin(3\alpha)}{3}=\frac{20*0,6}{3}=\frac{12}{3}=4.$$
Пример 8
Найти значение выражения \(\frac{12\sin(11^o)\cos(11^o)}{\sin(22^o)}=?\)
Замечаем, что \(22^o=2*11^o\) и воспользуемся синусом двойного угла:
$$\frac{12\sin(11^o)\cos(11^o)}{\sin(22^o)}=\frac{12\sin(11^o)\cos(11^o)}{2\sin(11^o)\cos(11^o)}=\frac{12}{2}=6.$$
Тригонометрические тождества
- $tgα={sinα}/{cosα}$
- $ctgα={cosα}/{sinα}$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^2α}$
$cosα=±√{1-sin^2α}$
- $tgα·ctgα=1$
- $1+tg^2α={1}/{cos^2α}$
- $1+ctg^2α={1}/{sin^2α}$
Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус
$sint=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos(α-β)+cos(α+β)}/{2}$
$sinα·sinβ={cos(α-β)-cos(α+β)}/{2}$
$sinα·cosβ={sin(α+β)+sin(α-β)}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Вычислить $sin12cos18+cos12sin18$
Данное выражение является синусом суммы
$sin12cos18+cos12sin18= sin(12+18)=sin30=0.5$
Задача (Вписать в ответ число)
Вычислить $sin{5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}$
Решение:
Данное выражение является синусом суммы
$sin {5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}=sin({π}/{12}+{5π}/{12})=sin {6π}/{12}=sin {π}/{2}=1$
Ответ: $1$
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Определение тригонометрических функций через окружность[править | править код]
Рис. 3. Определение тригонометрических функций через окружность.
Рис. 4. Tригонометрическиe функций угла α\alpha в тригонометрической окружности с радиусом, равным единице.
Пусть на плоскости задана прямоугольная система координат с началом в точке OO и с осями OX{OX} и OY{OY} (см. Рис. 3). Возьмём в этой системе координат окружность с центром в точке OO и радиусом, равным единице. Пусть отрезок OA{OA} поворачивается на произвольный угол ϑ\vartheta вокруг центра O.O.
Синусом угла ϑ\vartheta называется отношение ординаты точки AA к длине отрезка OA.{OA}. Обозначают sin Синус ϑ=ACOA.\sin\vartheta=\frac{AC}{OA}. Так как длина отрезка OA{OA} равна 11, то sin Синус ϑ=AC.\sin\vartheta={AC}.
Косинусом угла ϑ\vartheta называется отношение абсциссы точки AA к длине отрезка OA.{OA}. Обозначают cos Косинус ϑ=OCOA.\cos\vartheta=\frac{OC}{OA}. Так как длина отрезка OA{OA} равна 1, то cos Косинус ϑ=OC.\cos\vartheta={OC}.
Тангенсом угла ϑ\vartheta называется отношение ординаты точки AA к абсциссе точки AA. Обозначают tg Тангенс ϑ=ACOC\tg\,\vartheta=\frac{AC}{OC} (в англоязычной литературе tanϑ).\operatorname{tan}\vartheta ). Так как AC=sin Синус ϑ{AC}=\sin \vartheta и OC=cos Косинус ϑ,{OC}=\cos\vartheta, то tg Тангенс ϑ=sin Синус ϑcos Косинус ϑ.\tg\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}.
Котангенсом угла ϑ\vartheta называется отношение абсциссы точки AA к ординате точки AA. Обозначают ctg Котангенс ϑ=OCAC\ctg\,\vartheta=\frac{OC}{AC} (в англоязычной литературе cotϑ).\operatorname{cot}\vartheta ). Так как AC=sin Синус ϑ{AC}=\sin\vartheta и OC=cos Косинус ϑ,{OC}=\cos\vartheta, то ctg Котангенс ϑ=cos Косинус ϑsin Синус ϑ.\ctg\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}. Котангенс равен обратному значению тангенса: ctg Котангенс ϑ=1tg Тангенс ϑ.\ctg\,\vartheta=\frac{1}{\tg\,\vartheta}.
Секансом угла ϑ\vartheta называется отношение длины отрезка OA{OA} к абсциссе точки AA. Обозначают sec Секанс ϑ=OAOC.\sec\vartheta=\frac{OA}{OC}. Так как длина отрезка OA{OA} равна 1, то sec Секанс ϑ=1OC.\sec\vartheta=\frac{1}{OC}. Секанс равен обратному значению косинуса: sec Секанс ϑ=1cos Косинус ϑ.\sec\vartheta=\frac{1}{\cos\vartheta}.
Косекансом угла ϑ\vartheta называется отношение длины отрезка OA{OA} к ординате точки AA. Обозначают cosec Косеканс ϑ=OAAC\cosec \,\vartheta=\frac{OA}{AC} (в англоязычной литературе cscϑ).\operatorname{csc}\vartheta ). Так как длина отрезка OA{OA} равна 11, то cosec Косеканс ϑ=1AC.\cosec \,\vartheta=\frac{1}{AC}. Косеканс равен обратному значению синуса: cosec Косеканс ϑ=1sin Синус ϑ.\cosec \,\vartheta=\frac{1}{\sin\vartheta}.
Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.
I группа. Основные тождества
sin2α + cos2α = 1;
tgα = ____sinαcosα ; ctgα = ____cosαsinα ;
tgα·ctgα = 1;
1 + tg2α = _____ 1cos2α; 1 + ctg2α = _____ 1sin2α .
Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).
Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___ 1tgα и пользуйтесь формулами для тангенса.
Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю
Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи
Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.
11.4 Решение уравнения ctg α = y
Если
необходимо найти угол α при известном y,
то решением уравнения
ctg
α = y
будет
α
= arcctg y + πn,
n ϵ Z.
Задача.
Для заданного
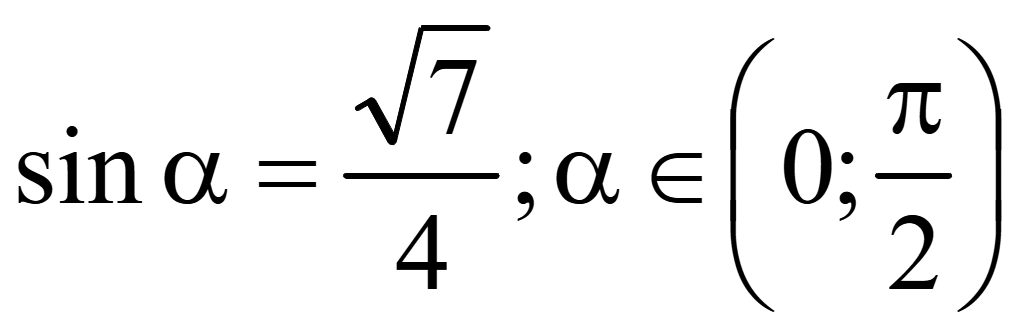 .
.
Найтиcosα.
Решение
sin2α
+ cos2α
= 1;
cos2α
= 1 — sin2α;
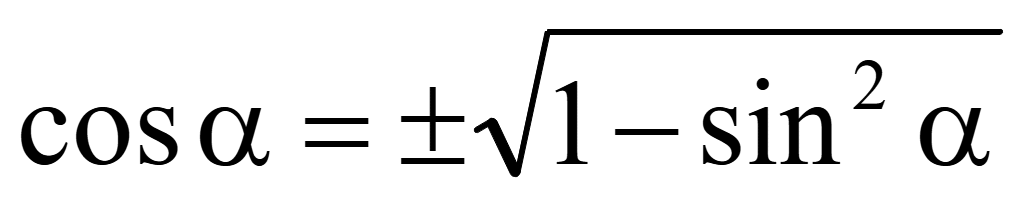 .
.
Так
как угол принадлежит первой координатной четверти, то косинус этого
угла положительный
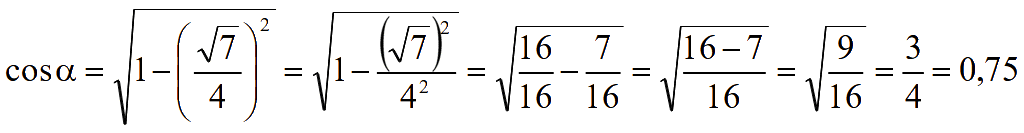
Ответ:
cosα
= 0,75.
Пример.
Решите уравнение
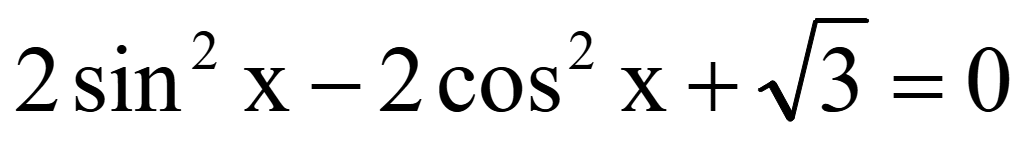
и
укажите корни уравнения наотрезке.
Решение
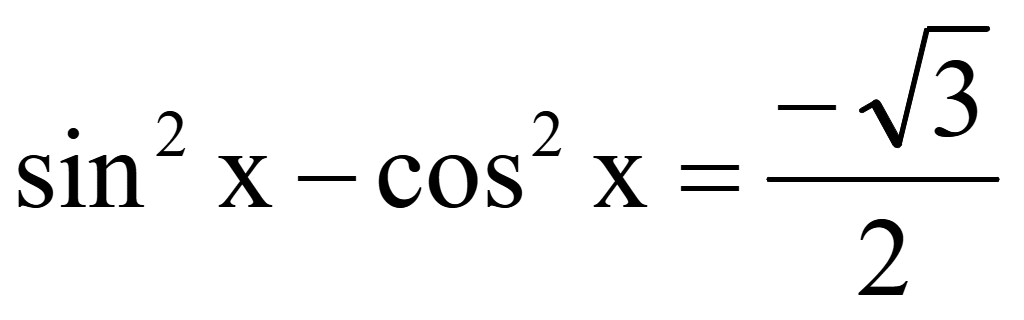
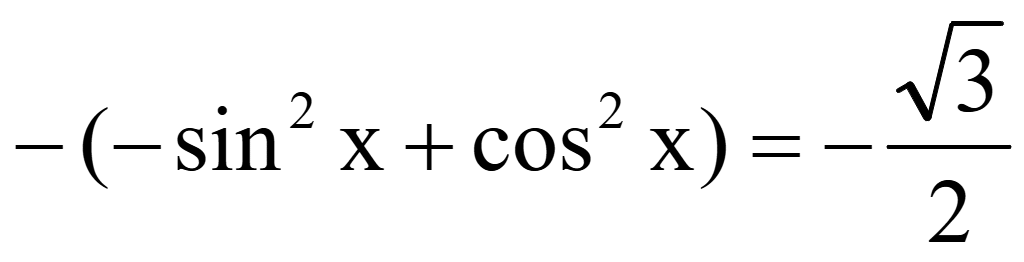
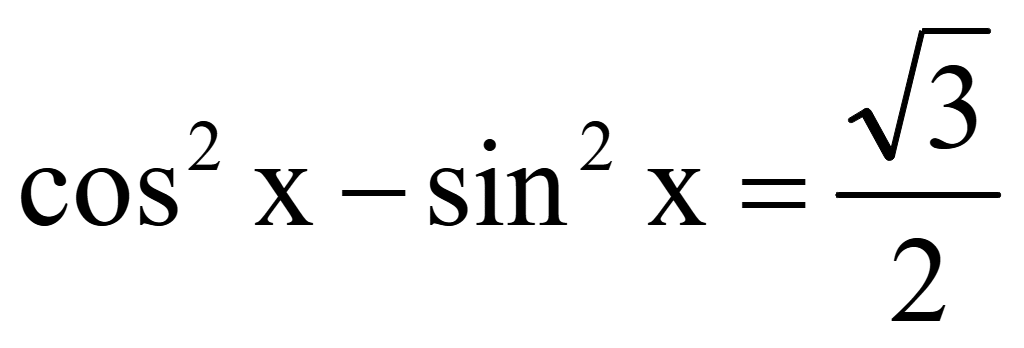
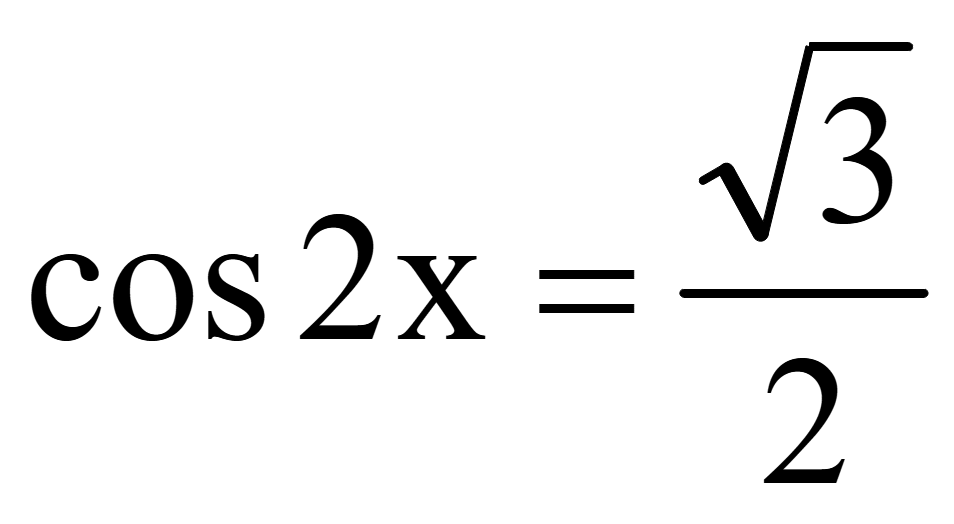
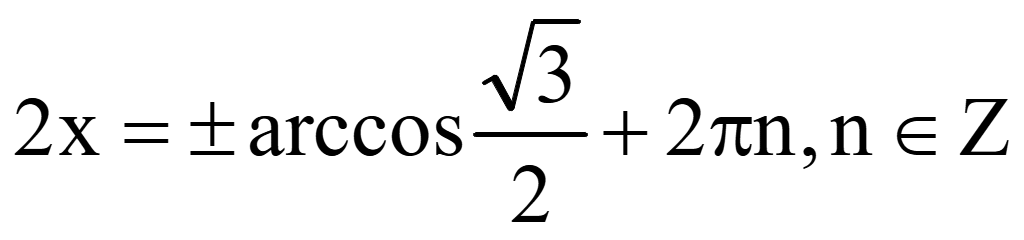
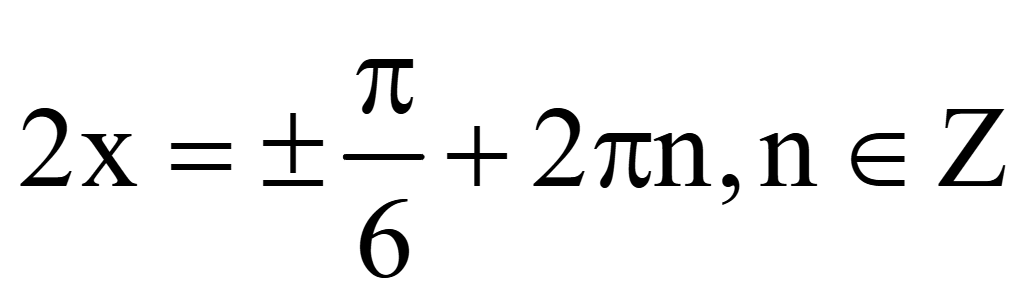

Найдем
корни уравнения на отрезке .
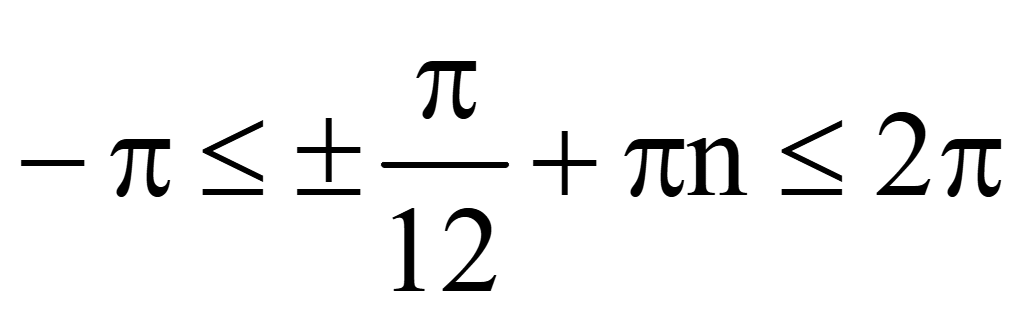
Разделим
на π все части неравенства
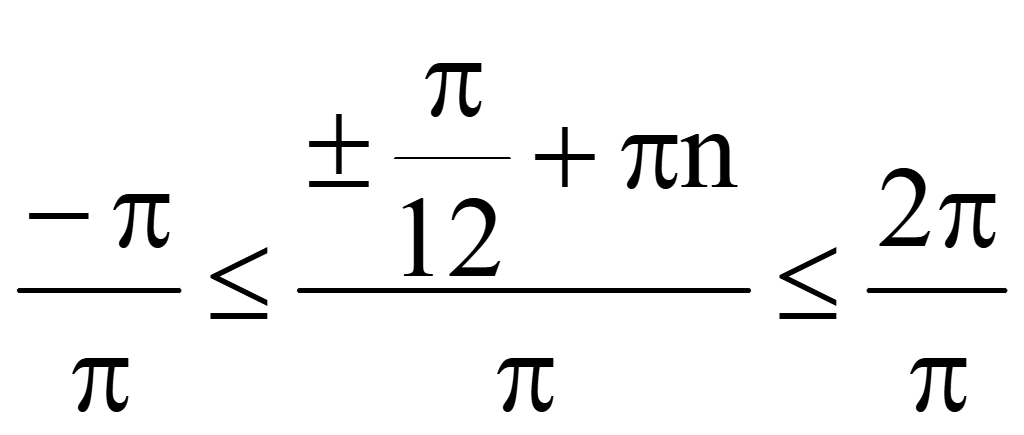
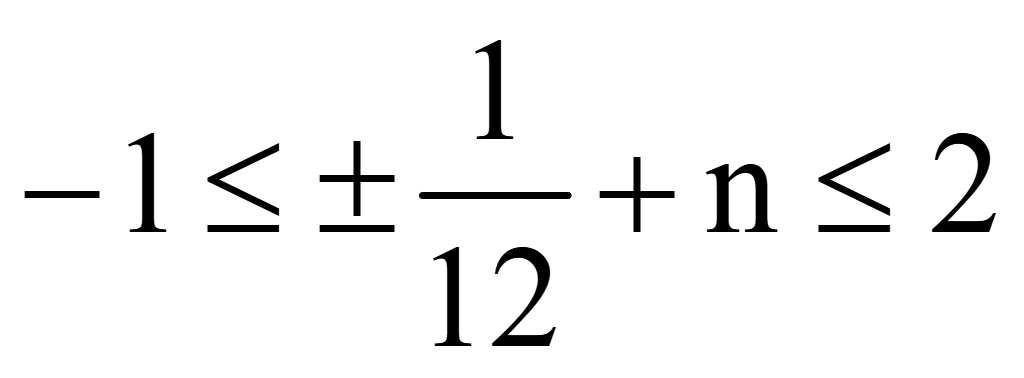
-12
≤ ±1+12n ≤ 24
Для
оценки значений n уберем ±1
-12
≤ 12n ≤ 24;
-1
≤ n ≤ 2;
Выражение
при
n = -2 значения
меньше заданного отрезка [-π;
2π
При
n = -1
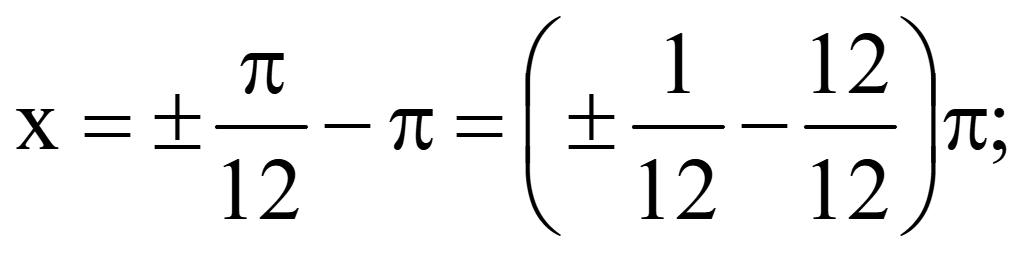
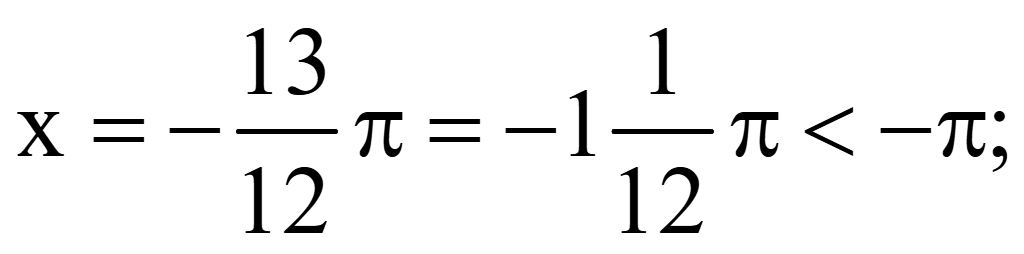
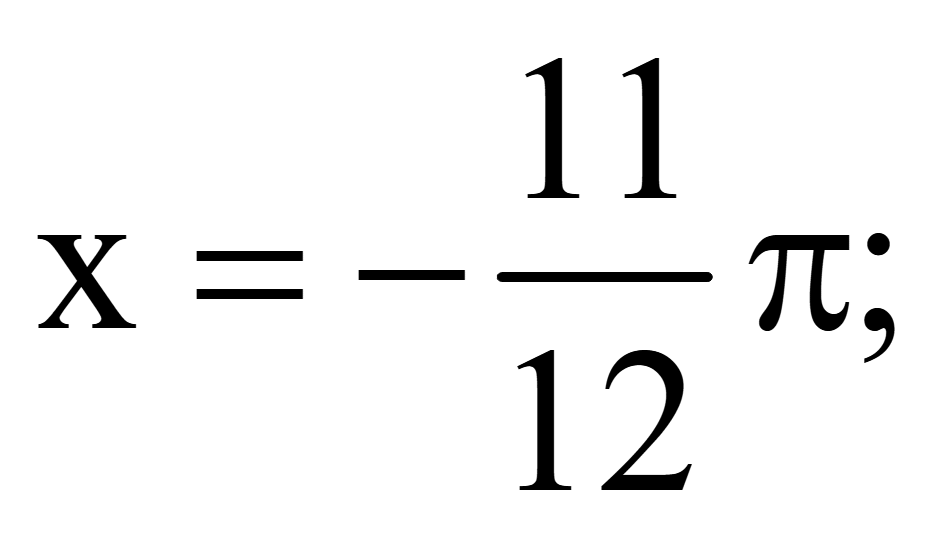
При
n =
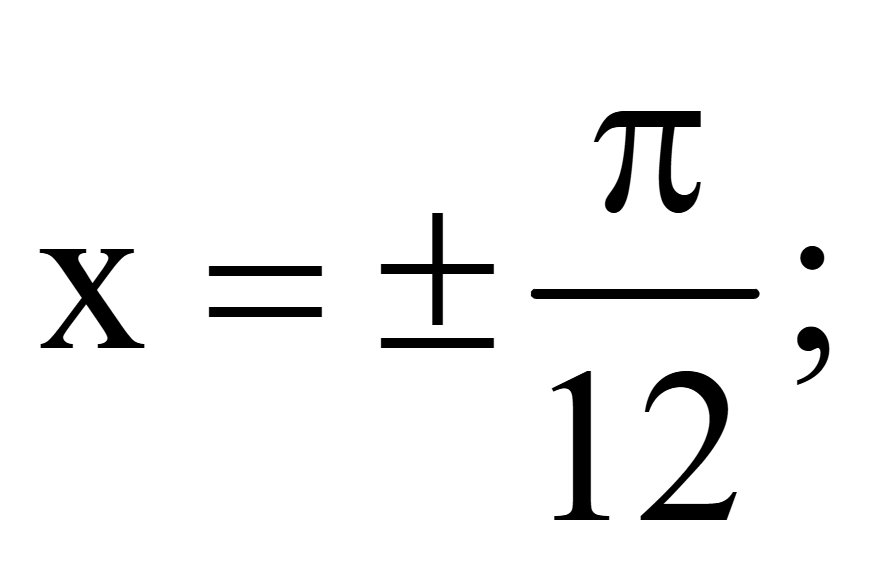
При
n = 1
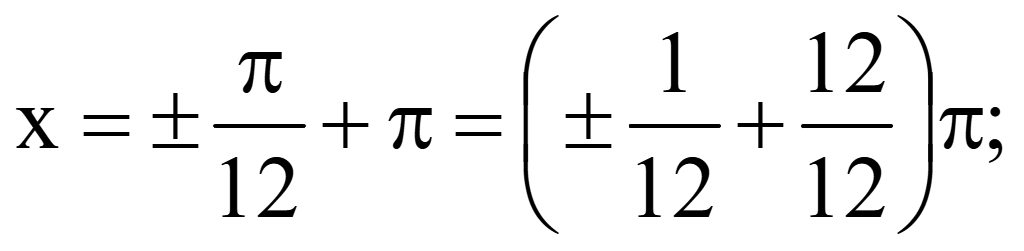

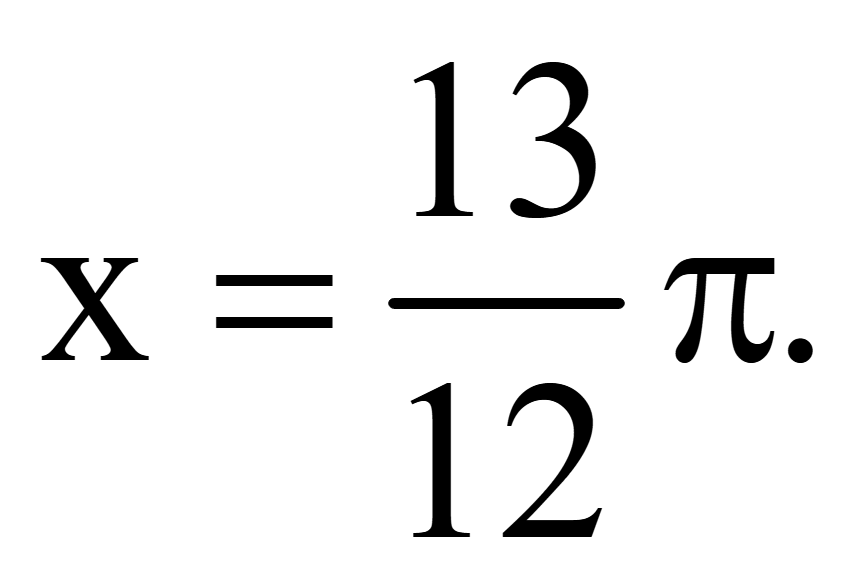
При
n = 2
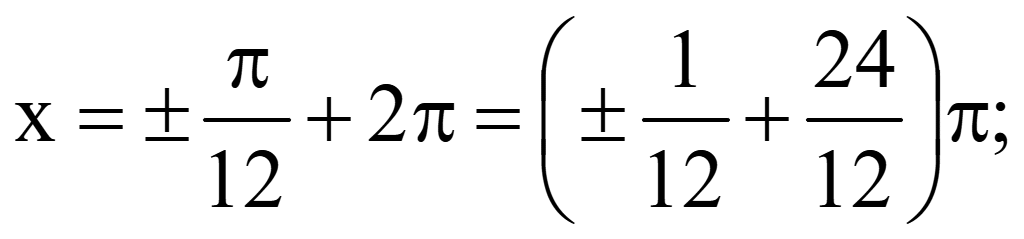
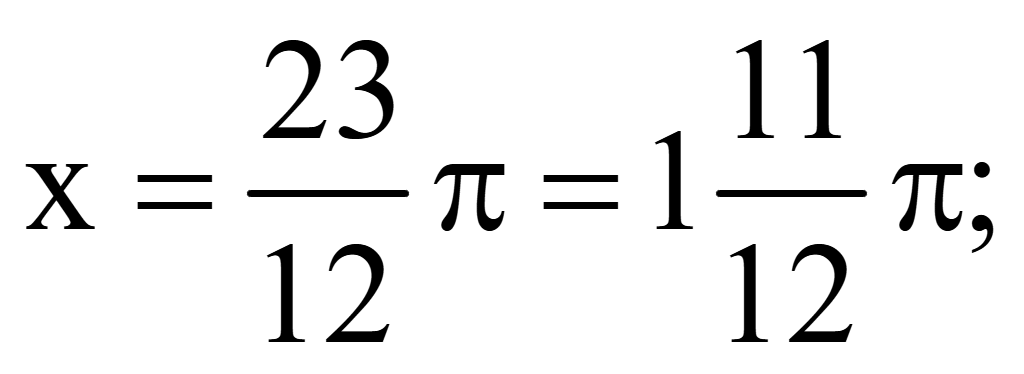
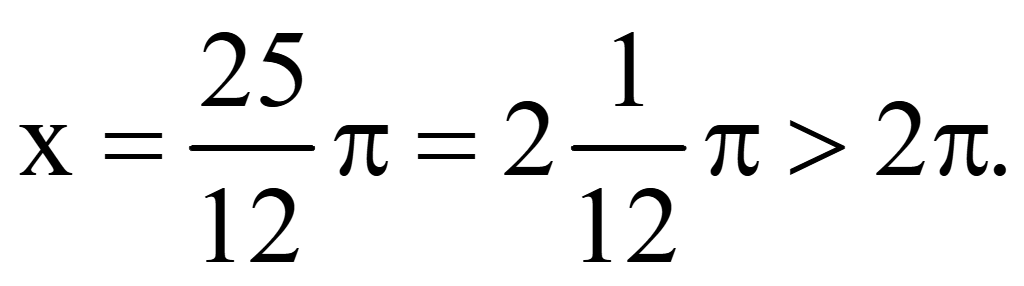
Ответ:
.
6
корней уравнения на промежутке :
 .
.
Пример.
Решите уравнение
3sin2x
+
ctg2x
sin2x
— 2
=
0
и
укажите корни уравнения на отрезке
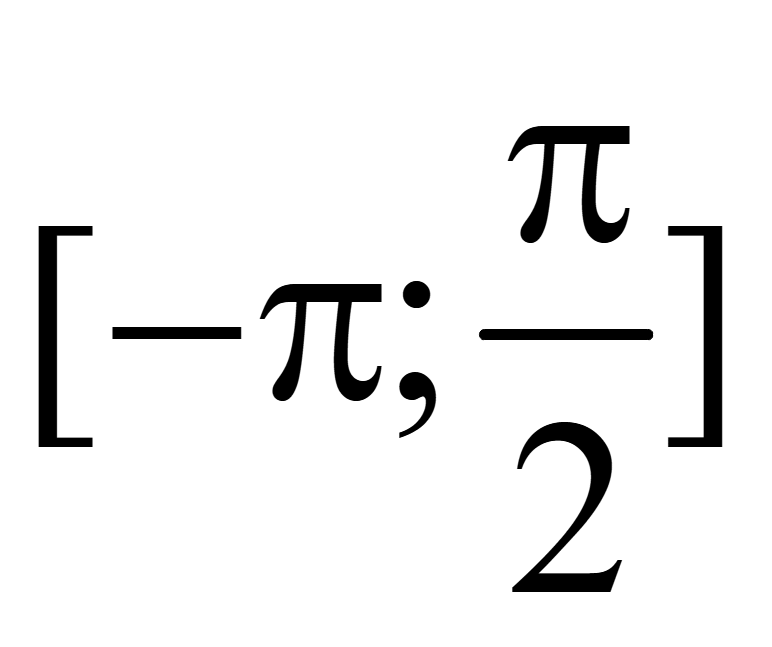 .
.
Решение
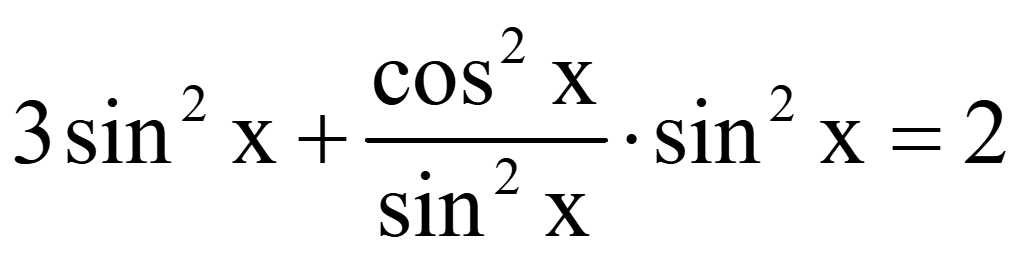
3sin2x
+ cos2x
= 2;
3sin2x+
1 — sin2x=
2;
2sin2x
= 1;
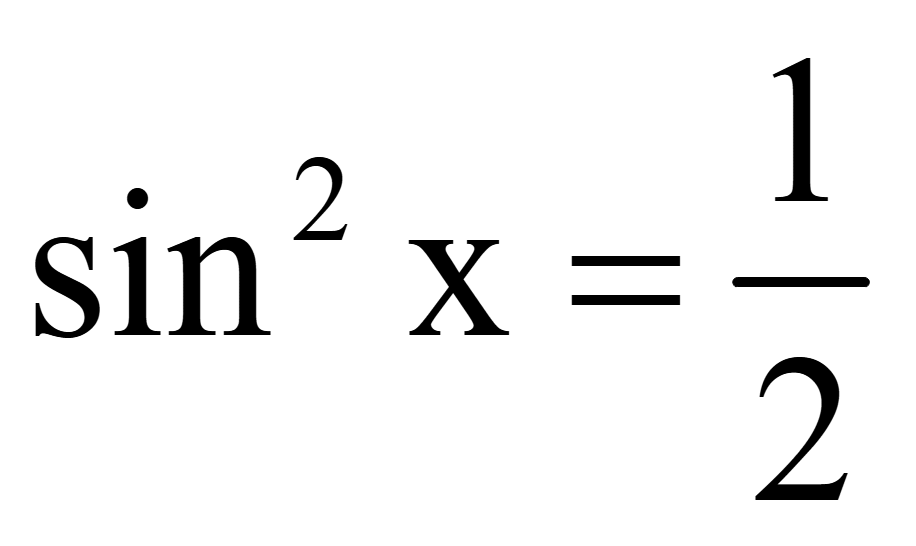
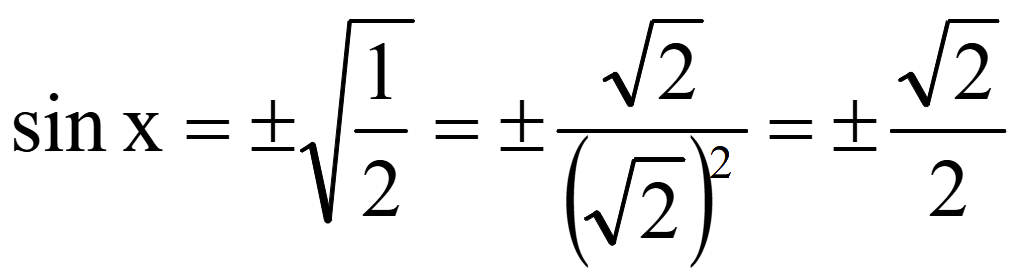

Функция
нечетная: arcsin (-x)
= -arcsin x, поэтому
вынесем ±
за arcsin
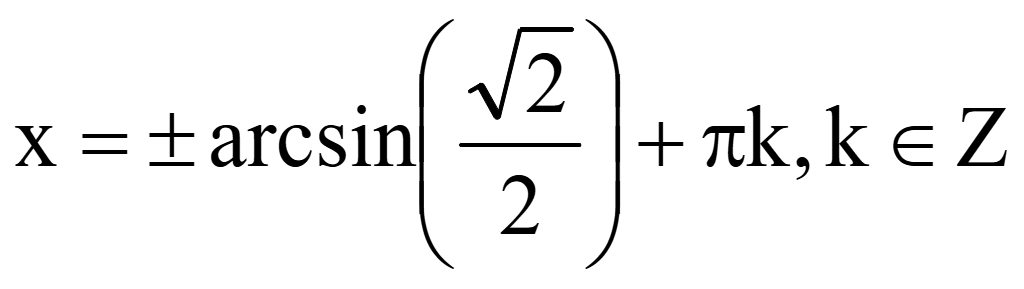

Выберем
корни уравнения на промежутке
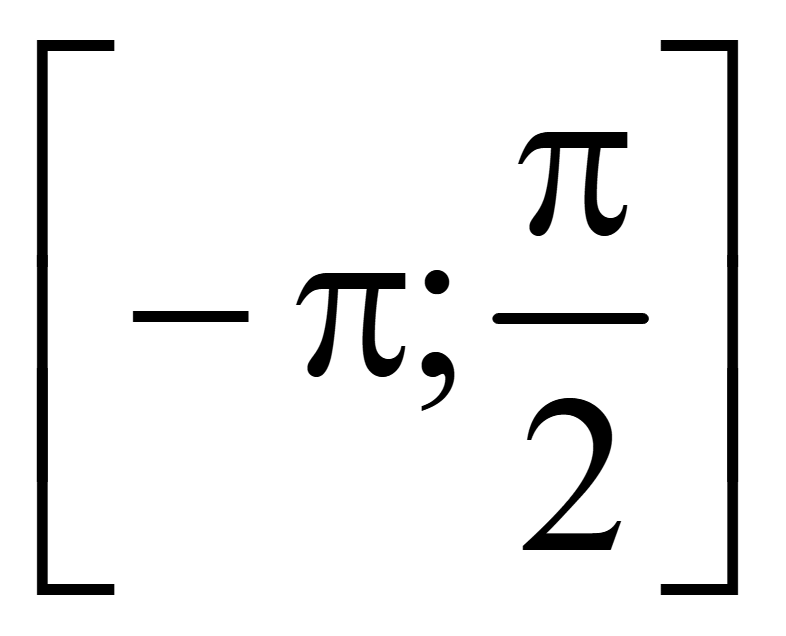
.
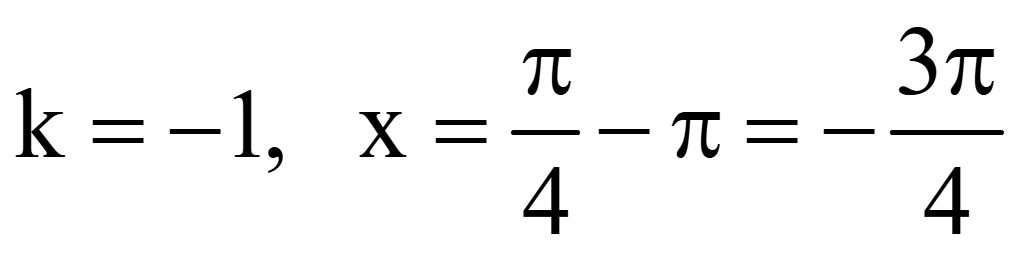
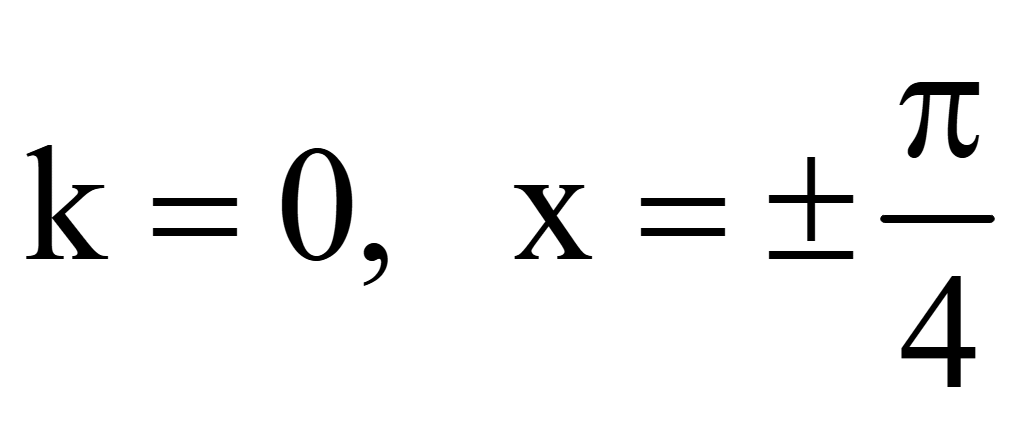
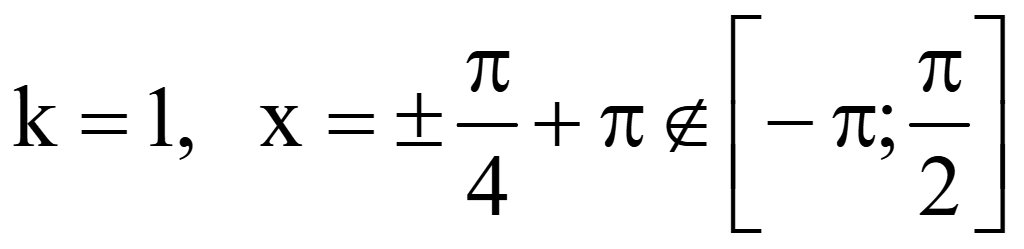 .
.
Ответ:

.
3 корня уравнения на промежутке
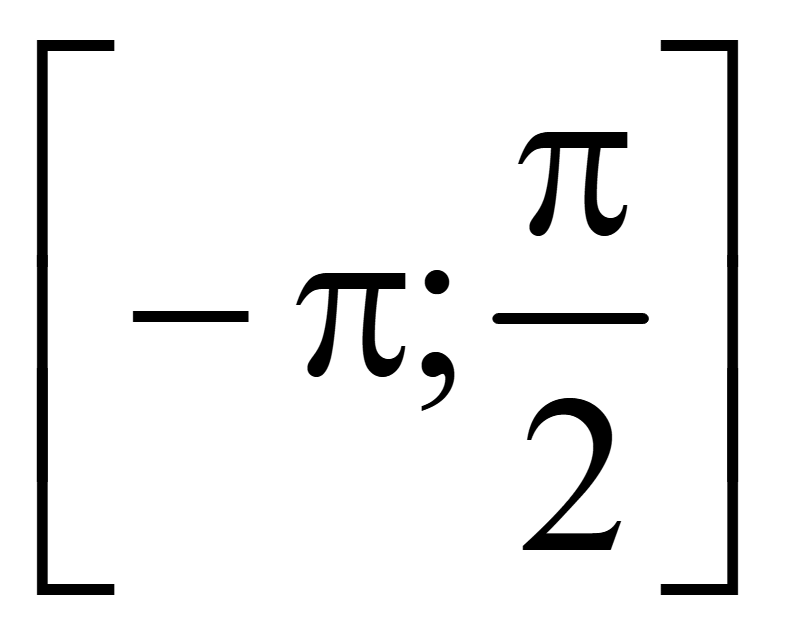
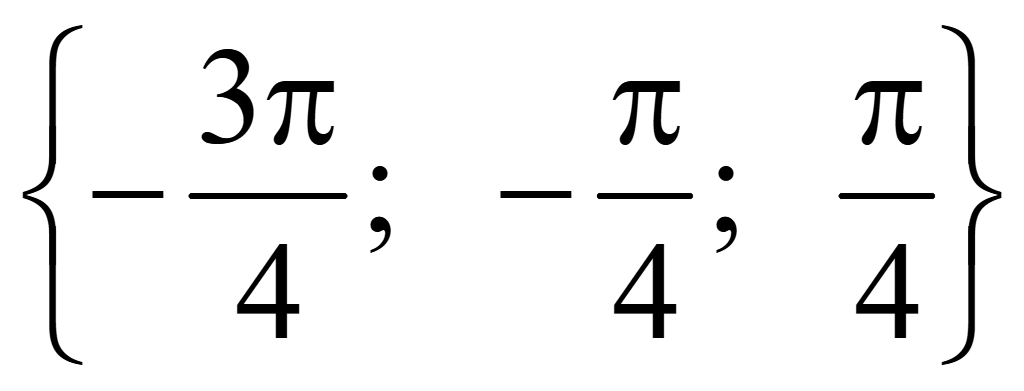
.
Пример.
Решите уравнение
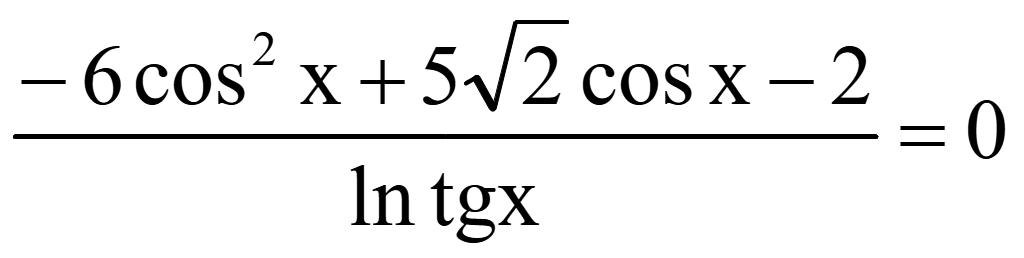
Решение
ОДЗ:
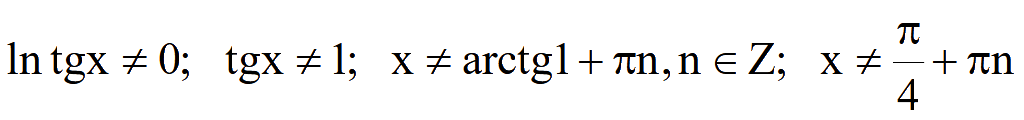 .
.
Исходное
уравнение равно нулю тогда, когда числитель равен нулю
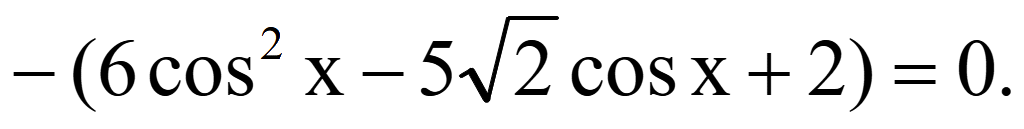
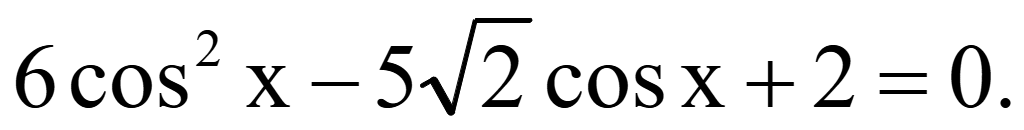
Подстановка
для упрощения уравнения t = cosx

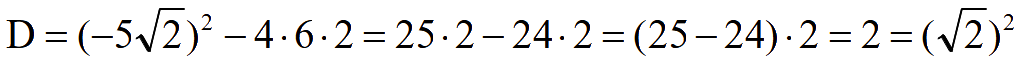
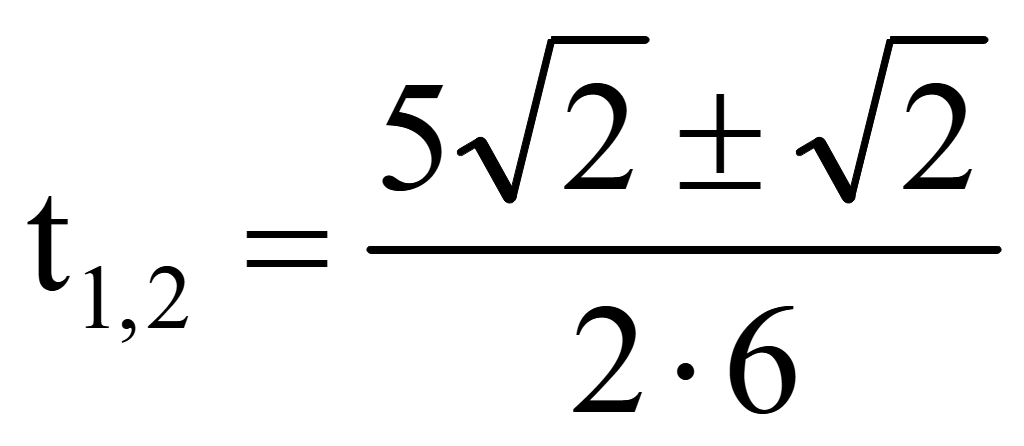
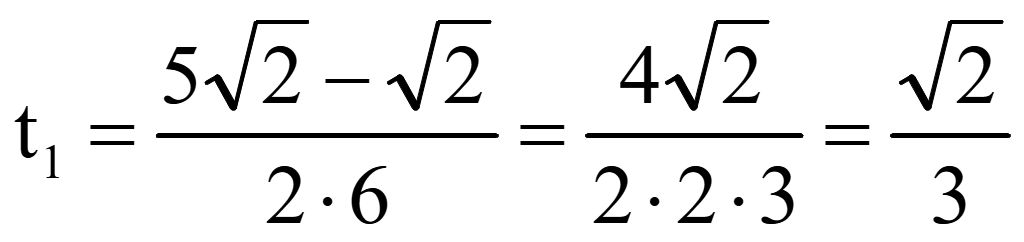

Обратная
замена переменной t
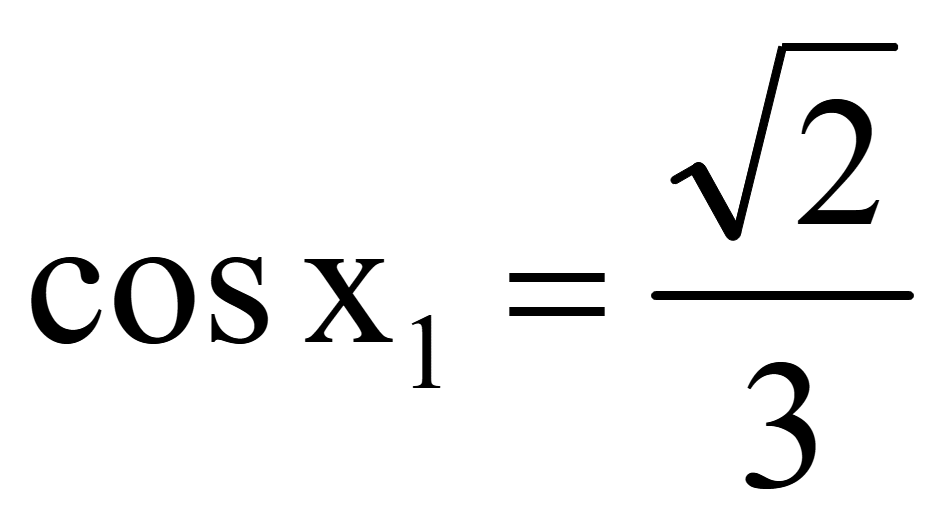
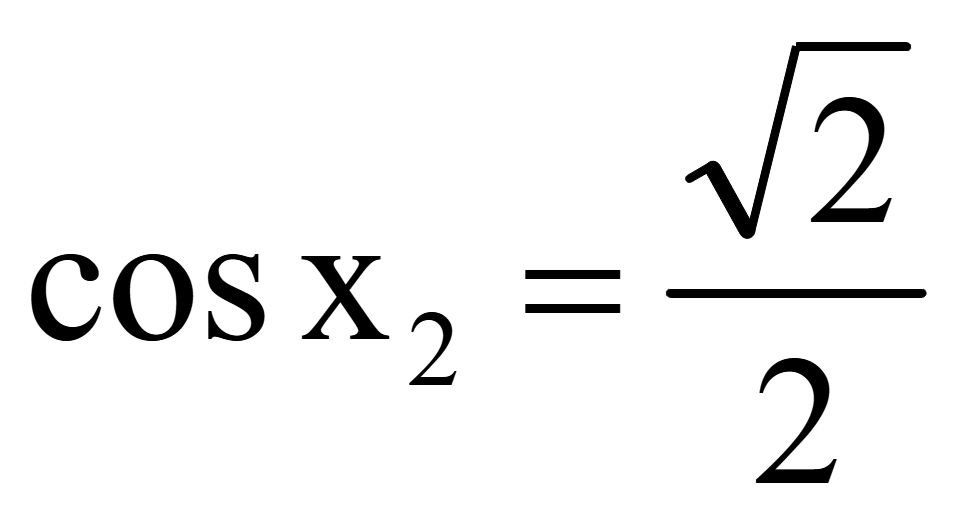
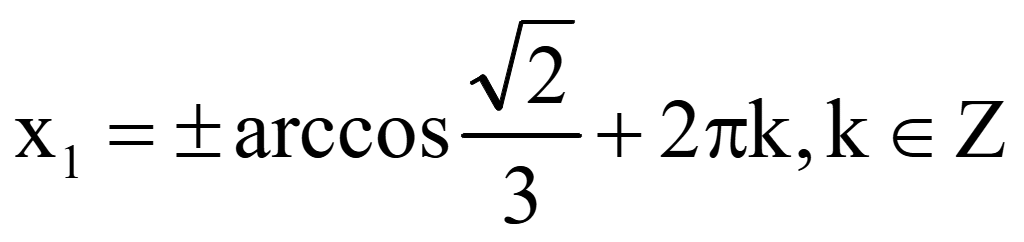
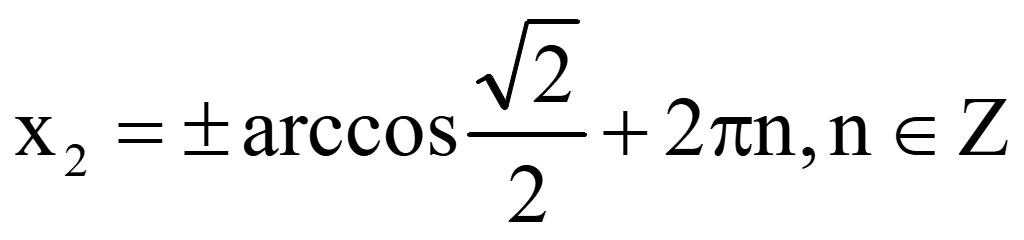
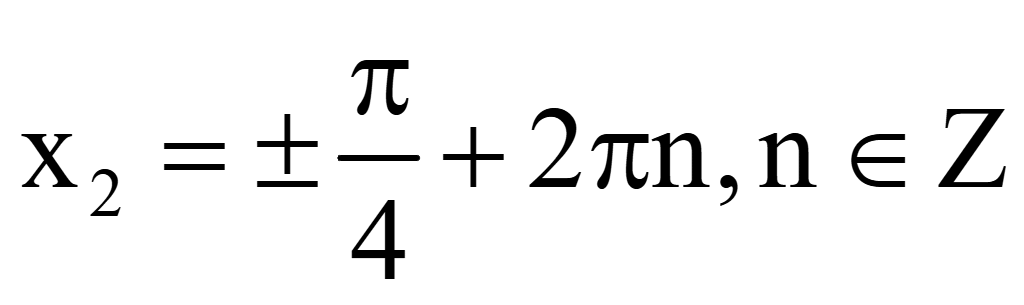 ,
,
но
корень
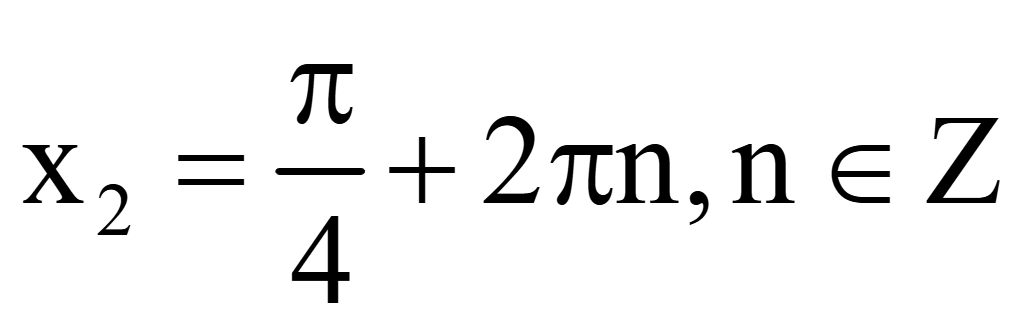
не
удовлетворяет области определения, поэтому остается корень
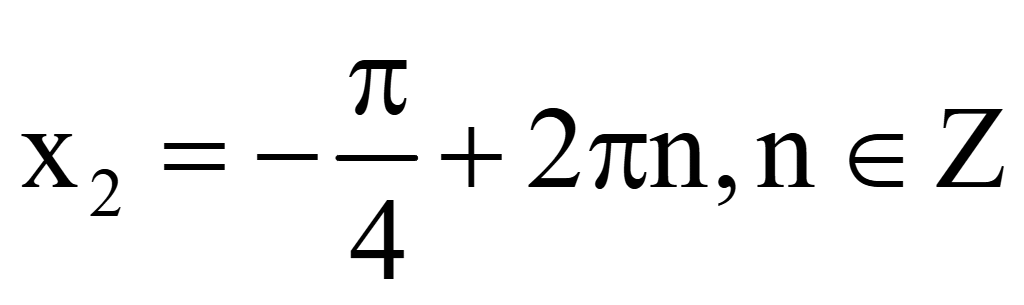 .
.
Ответ:
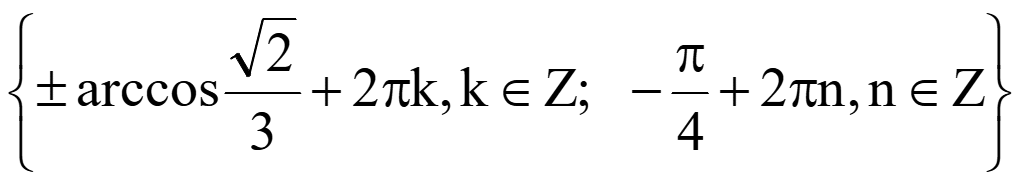 .
.
Пример.
Решите уравнение
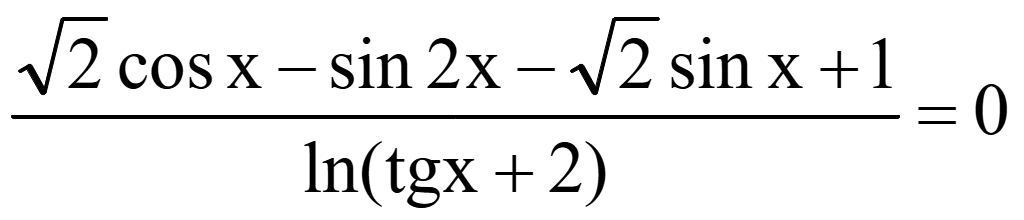
Решение
ОДЗ:
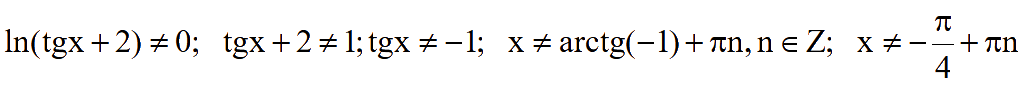
Исходное
уравнение равно нулю тогда, когда числитель равен нулю
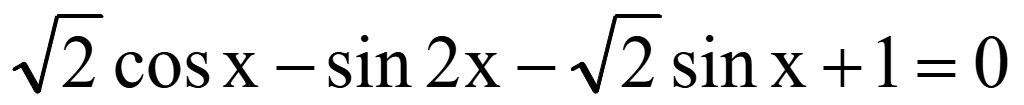

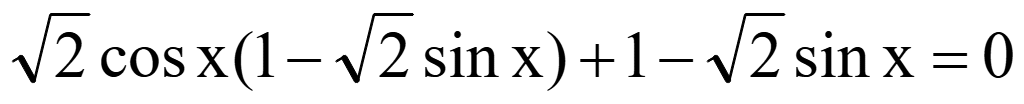
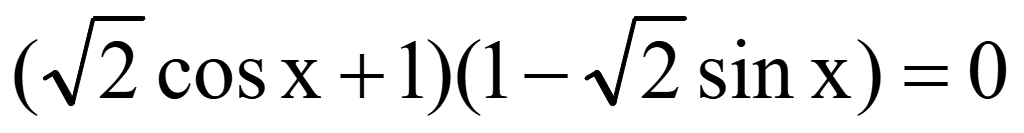
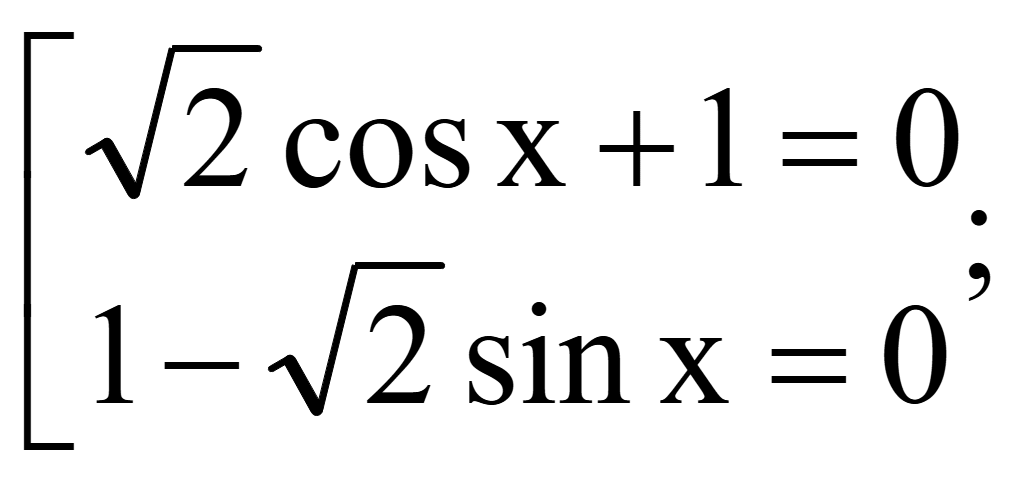
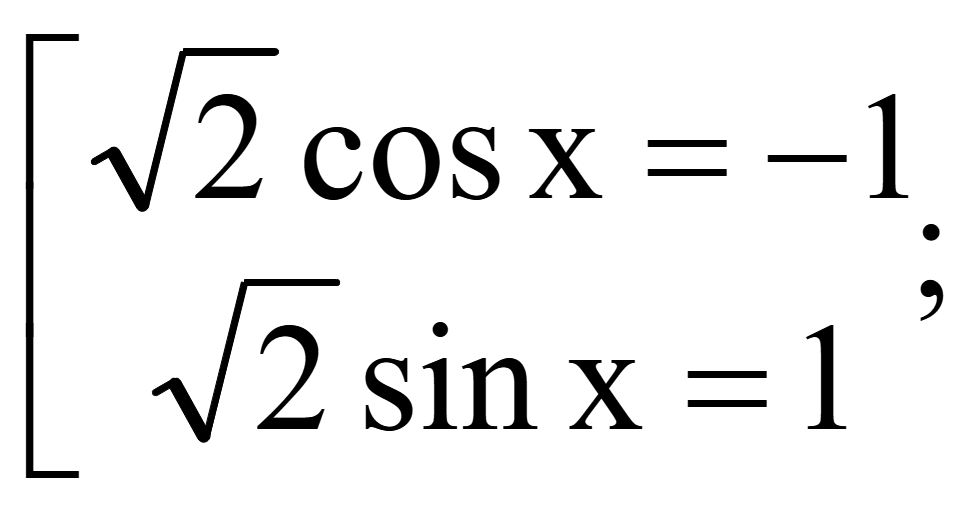
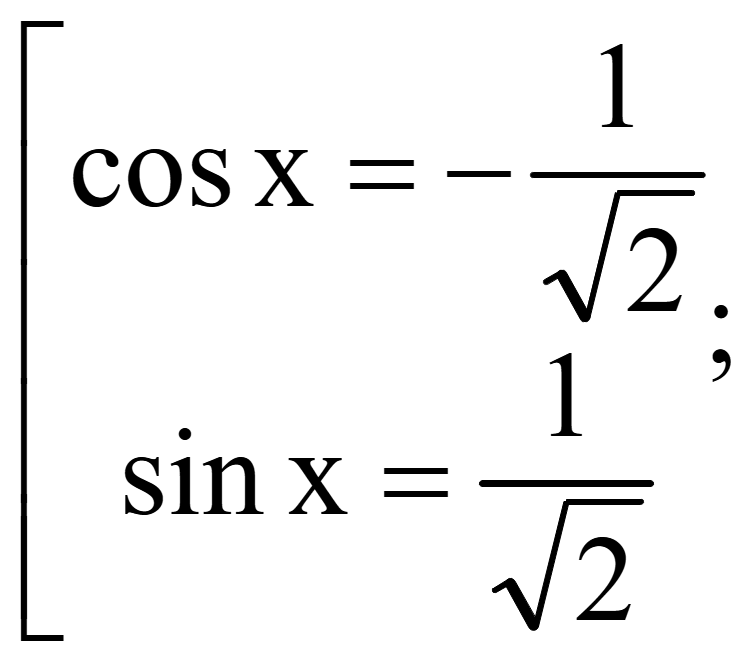
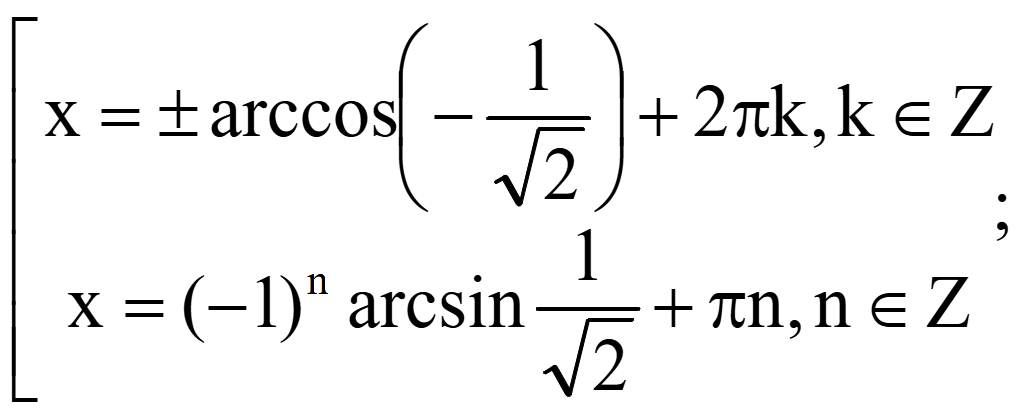
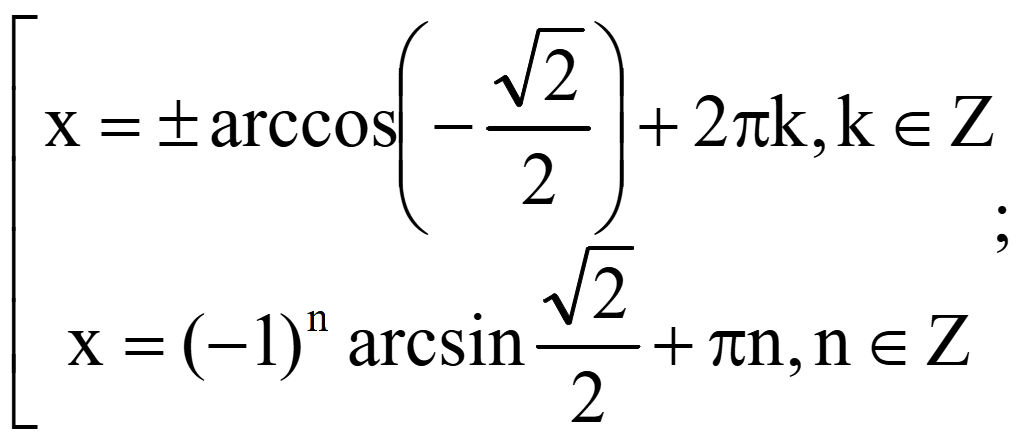
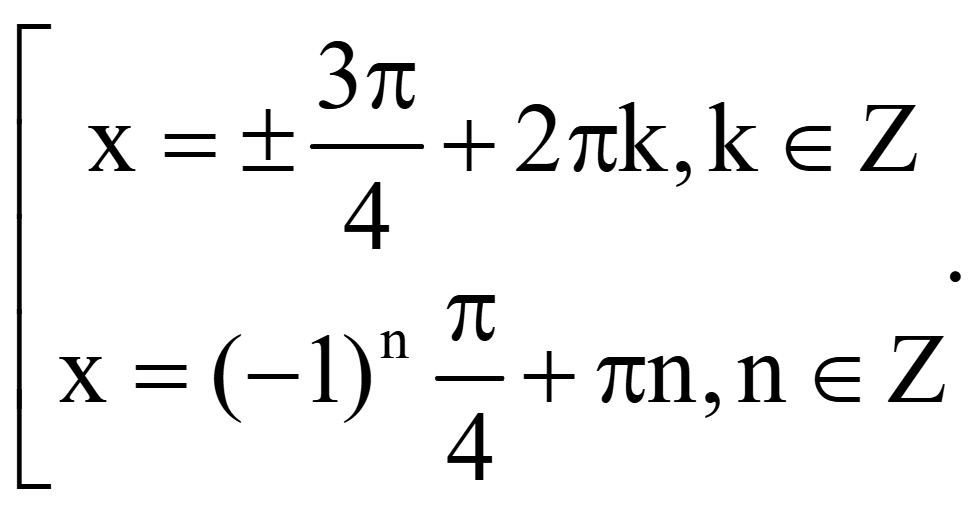
Ответ:
Пример.
Решить уравнение
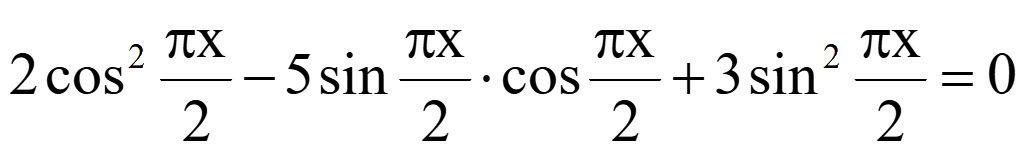
Решение
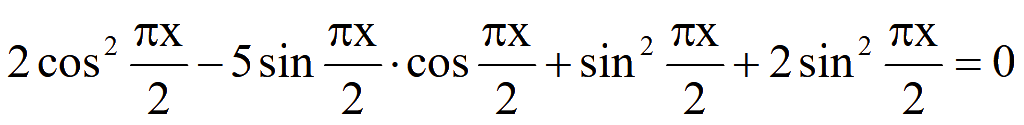
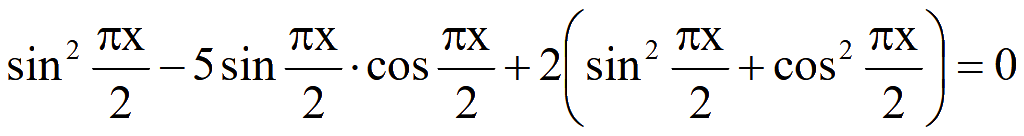
sin2α
+ cos2α
= 1
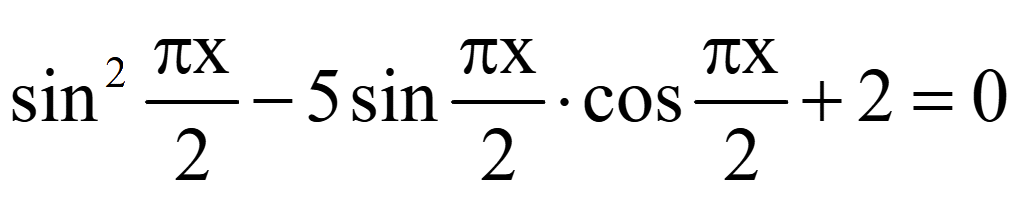
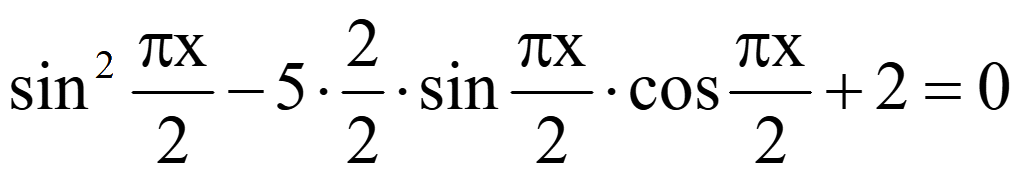
sin2α
= 2sinαcosα
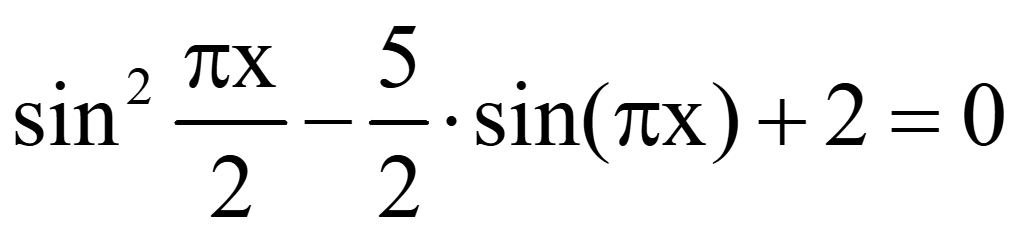
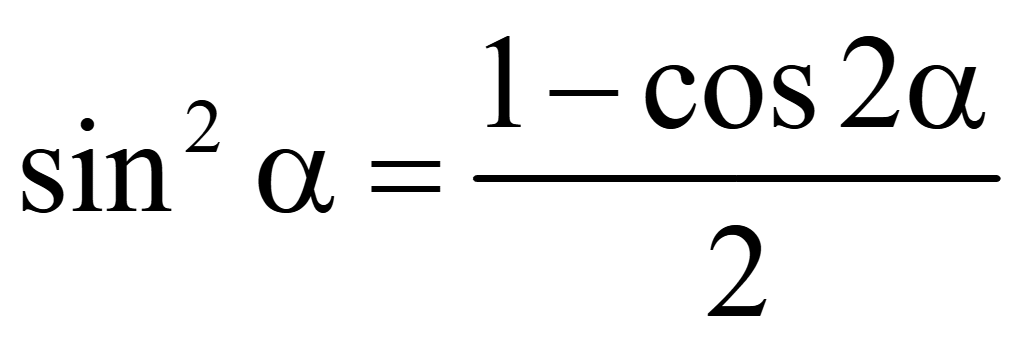
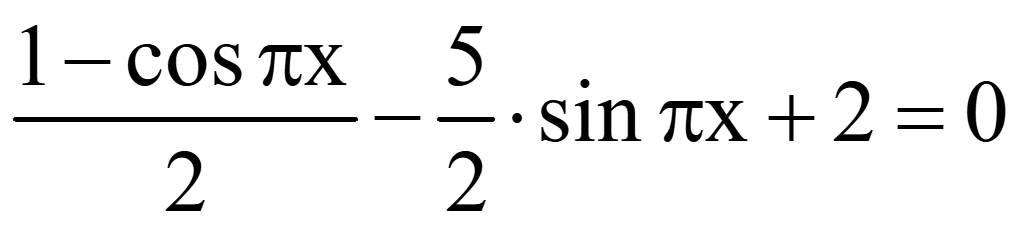
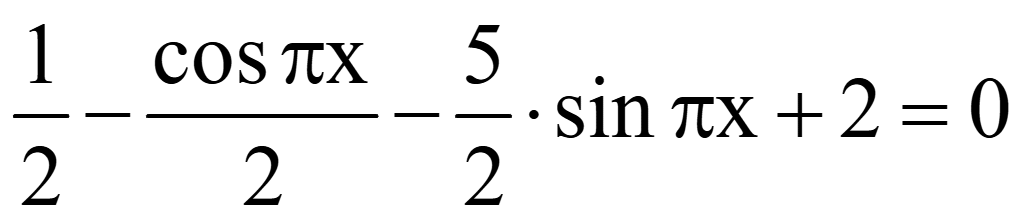
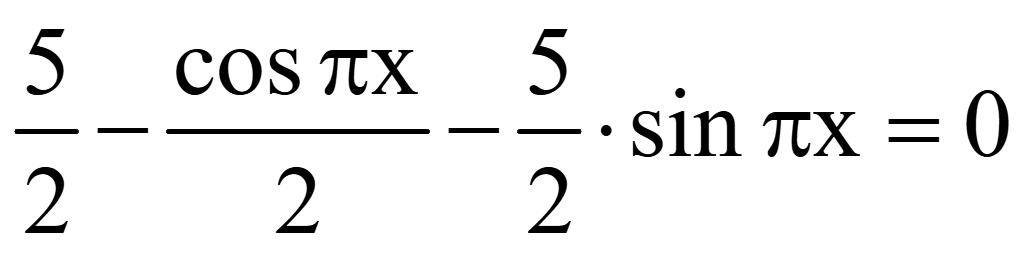
Помножим
на 2
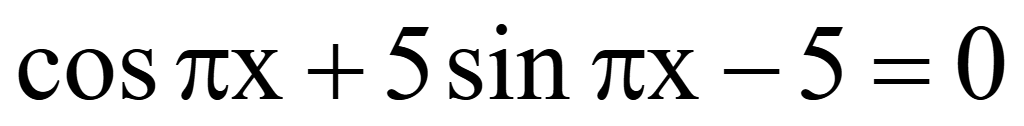
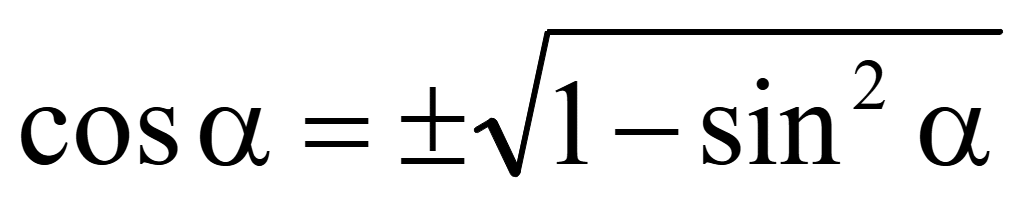

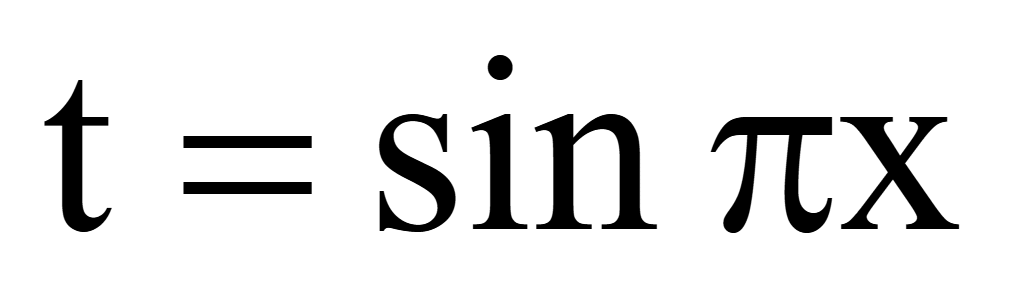
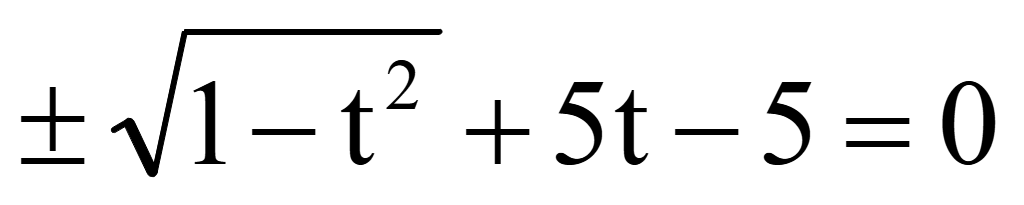
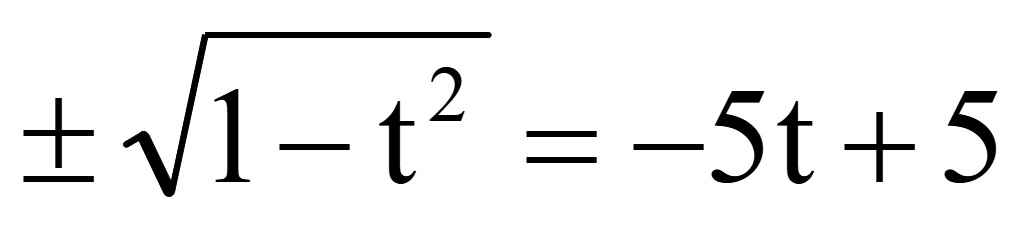
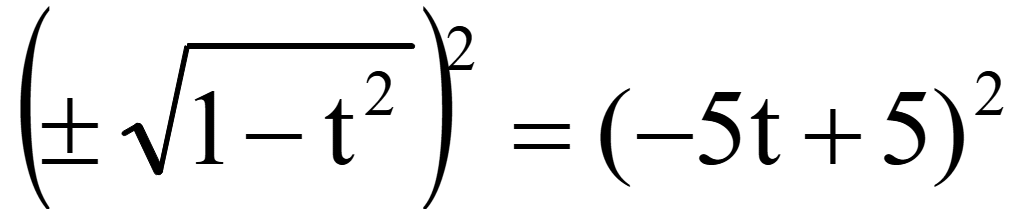
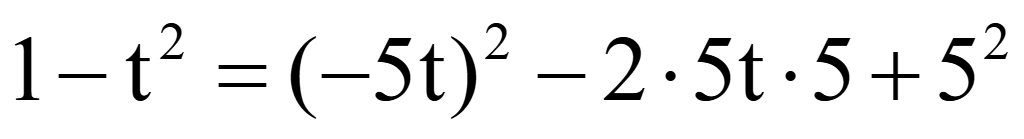
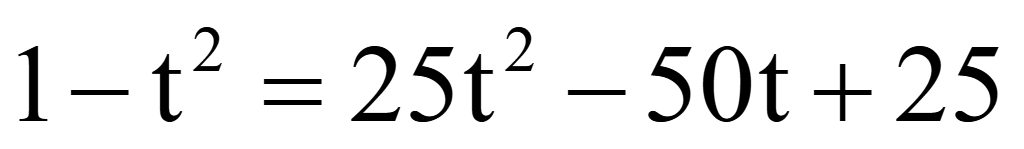
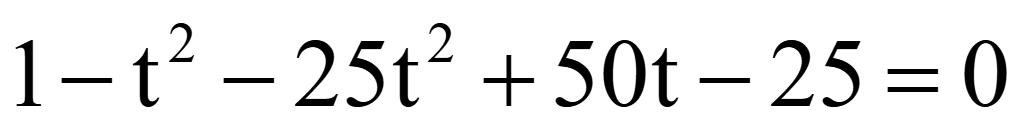
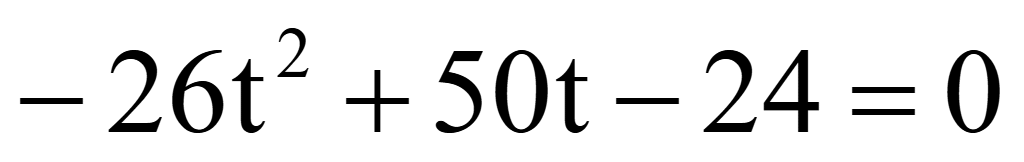
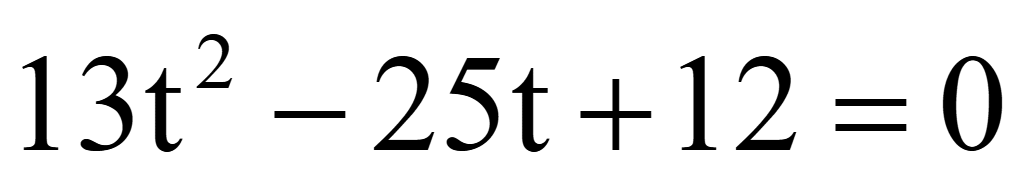
Основные тригонометрические тождества формул приведения
Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.
Существует два основных способа, использования формул приведения:
- Если угол можно записать как (π/2 ±α) или (3*π/2 ±α), то название функции меняется с косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде (π±α) или (2*π±α), то название функции не меняется.
- Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.
Формулы приведения, примеры:
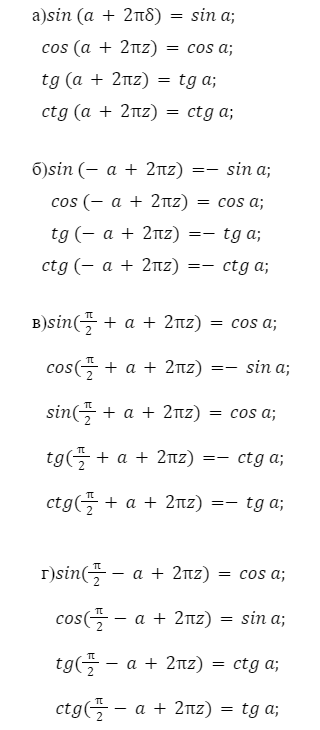
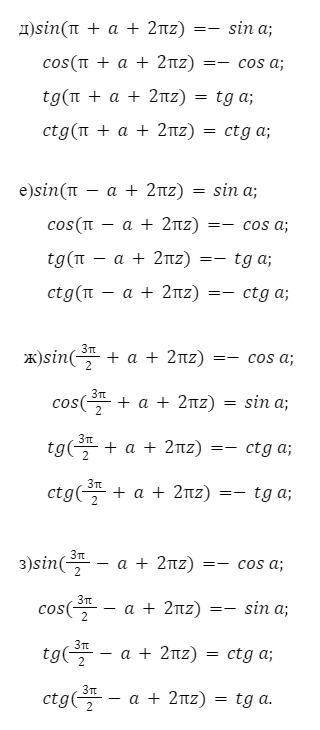
При расчетах очень часто возникают трудности при вычислении больших значений степеней. Для этого в тригонометрии, существует такое понятие как понижение значения степени.
Тождества понижения степени, помогают справиться с этой непростой задачей. Они выражают степень sin и cos через sin и cos первой степени, но определенного кратного угла. Поэтому, тригонометрические уравнения снижают степень первоначальных функций с определенной до первой степени, но при этом повышают кратность угла от до n.
Тригонометрические формулы для косинуса и синуса понижения степени, записываются в следующем виде:
После преобразования основных формул понижения получаем их общий вид. Рассмотрим на примерах ниже.
Для четных значений уравнения:
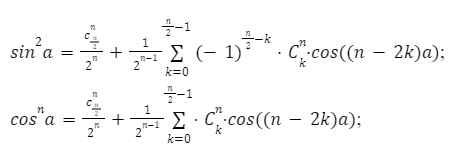
Для нечетных значений уравнения:
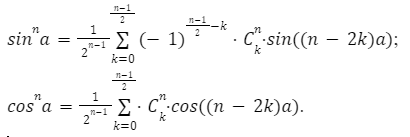
Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется
Попробуйте сами:
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2
Производные и интегралы[править | править код]
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
(sin Синус x)′=cos Косинус x,( \sin x )’ = \cos x \,,
(cos Косинус x)′=−sin Синус x,( \cos x )’ = -\sin x \,,
(tg Тангенс x)′=1cos Косинус 2x,( \tg x )’ = \frac{1}{\cos ^2 x},
(ctg Котангенс x)′=−1sin Синус 2x.( \ctg x )’ = -\frac{1}{\sin ^2 x}.
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
∫sin Синус xdx=−cos Косинус x+C,\int\sin x\, dx = -\cos x + C \,,
∫cos Косинус xdx=sin Синус x+C,\int\cos x\, dx = \sin x + C \,,
∫tg Тангенс xdx=−ln Натуральный логарифм |cos Косинус x|+C,\int\tg x\, dx = -\ln \left| \cos x\right| + C \,,
∫ctg Котангенс xdx=ln Натуральный логарифм |sin Синус x|+C.\int\ctg x\, dx = \ln \left| \sin x \right| + C \,.
Стандартные углы
Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
- Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
\
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:
\
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
\
И с углом 30°:
\
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:
\
Итак, мы знаем синус
Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$
Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
И наоборот:
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
Что такое тригонометрические функции числового аргумента
Равнозначным является и такое объяснение: тригонометрические функции представляют собой выражение того, как связаны хорды и высоты с центральным углом дуги в круге. Рассматриваемые функции активно используют в разных научных областях. Можно наблюдать расширение определения тригонометрических функций по мере того, как развивалась математика. К примеру, в настоящее время роль аргумента могут играть какие-либо вещественные или комплексные числа.
Представим, что имеется некое действительное число, и обозначим его t. Данному числу однозначно соответствует конкретное число sin(t). Правило соответствие достаточно сложное. Поэтому рассмотрим его детально.
Поиск значения sin(t) относительно числа t реализован по следующему алгоритму:
- Расположение координатной окружности на плоскости таким образом, что центр круга находится в точке начала координат, а у начальной точки А, принадлежащей окружности, следующие координаты (1; 0).
- Поиск точки на окружности, которая бы соответствовала числу t.
- Определение ординаты найденной точки.
- Полученная ордината является искомым значением sin(t).
В действительности здесь говорится о приведении функции s = sin(t) при t в виде какого-либо действительного числа. По предыдущим курсам тригонометрии уже известны определенные свойства рассматриваемой функции, а также некоторые ее значения, к примеру:
Кроме того, с предыдущих уроков уже имеется некоторое представление о таких функциях, как Перечисленные функции носят название тригонометрических функций числового аргумента t.
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
`cos \ \alpha+sin \ \alpha=\sqrt{2} \ cos (\frac{\pi}4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt{2} \ sin (\frac{\pi}4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \ cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ ctg \2\alpha`
Следующие формулы преобразовывают сумму и разность единицы и тригонометрической функции в произведение.
`1+cos \ \alpha=2 \ cos^2 \frac{\alpha}2`
`1-cos \ \alpha=2 \ sin^2 \frac{\alpha}2`
`1+sin \ \alpha=2 \ cos^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1-sin \ \alpha=2 \ sin^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Взаимосвязь тригонометрических функций
Между всеми тригонометрическими функциями существует взаимная связь, благодаря которой неизвестное значение одной из них можно определить, зная значение другой функции. Наиболее распространено использование в решении подобных заданий основного тригонометрического тождества.
Заметим, что с помощью данного тождества можно вычислить значение косинуса при известном значении синуса. Допустима и обратная операция.
Другими важными и полезными формулами являются уравнения, описывающие, каким образом между собой связаны синус и косинус с тангенсом и котангенсом.
Рассмотрим детально две последние представленные формулы. С помощью данных закономерностей можно записать другое тригонометрическое тождество.
При решении этих задач было указано две полезные формулы
Обратим на них внимание
Примеры решения задач

Задачи на нахождение знака попадаются редко, поскольку они являются довольно простыми. Рекомендуется потренироваться в нахождении знака. Для этого можно придумать углы любой меры (радианной или градусной).
После решения следует проверить результат, подставив значения в тригонометрический калькулятор. Его можно найти в стандартных программах операционных систем Windows, Linux и Mac (расширенная версия инструмента)
Кроме того, следует обратить внимание на то, что линия должна проходить по направлению, которое зависит от знака. Необходимо также учитывать четность или нечетность, а также периодичность каждой функции.
Положительное значение
Для изготовления детали следует рассчитать значение тригонометрических функций угла 225 градусов. В этой задаче ничего не сказано про знаки функций. Из-за этого и делают ошибки. Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
- Перевод градусной меры в радианную: 5ПИ/4.
- Значение находится в III четверти, следовательно: sin<0, cos<0, tg>0 и ctg>0.
- -sin(ПИ + ПИ/4) = -sin(ПИ/4) = -cos(ПИ/4) = -sqrt(2)/2.
- tg(ПИ/4) = ctg(ПИ/4) = -sin(ПИ/4) / -cos(ПИ/4) = 1.
После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.
Свыше 2ПИ
Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6. Решается она следующим образом:

- Следует выделить целую часть из -26ПИ/6 и привести к удобному виду: 26/6 = 4 + 2/6 = 4 + 1/3. Угол находится в IV четверти (движение по часовой стрелке).
- -sin(4ПИ + ПИ/3) = -sin(ПИ/3) = — sqrt(3)/2.
- cos(ПИ/3) = 1/2.
- -tg(ПИ/3) = — sqrt(3).
- -сtg(ПИ/3) = — 1/sqrt(3).
Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.
Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.

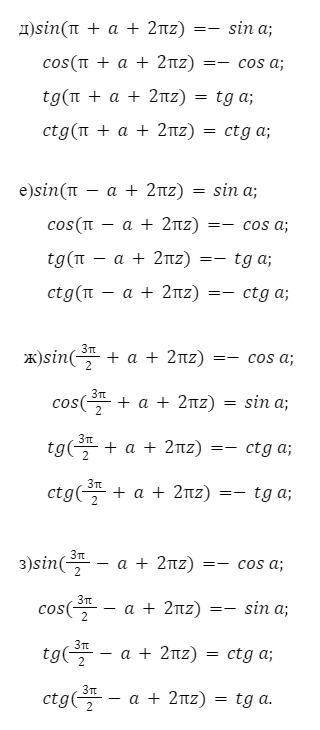





![§ 5. тригонометрические функции и их основные свойства [1950 новоселов с.и. - обратные тригонометрические функции]](http://mse52.ru/wp-content/uploads/8/1/e/81e85194b2582b3c4daf82919af1634e.jpeg)





![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://mse52.ru/wp-content/uploads/c/4/4/c449d506128ff91be961686849bfcab9.jpeg)















