Решение производной для чайников: определение, как найти, примеры решений

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

.

Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем
требуемую условием задачи производную всей функции:

А проверить решение задачи на производную можно на калькуляторе производных онлайн.

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями».

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде ,
то Вам на урок «Производные простых тригонометрических функций».

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн.

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :

Проверить решение задачи на производную можно на калькуляторе производных онлайн.

Задачи на определение наибольшего (наименьшего) значения функции на отрезке.

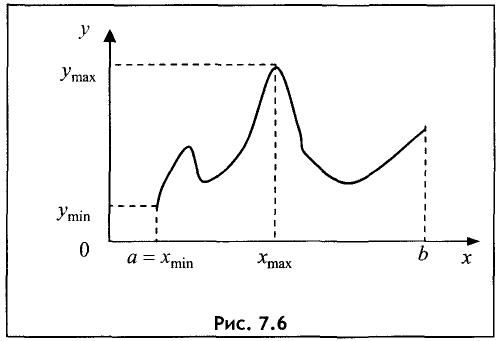
Непрерывная на отрезке функция достигает своего наименьшего и наибольшего значений либо во внутренних точках промежутка, либо на его концах. Поэтому для решения задач этого раздела достаточно определить значения функции в точках экстремума и сравнить их с её значениями на концах отрезка. Выявлять тип экстремума необязательно.

посмотреть здесь.

Задача 7

Найдите наибольшее значение функции на отрезке .

D(f) = (−∞;+∞).y’ = 3×2 + 4x + 1. Функция непрерывна на всей области определения. Точек, где y’ не существует, нет.Решаем уравнение y’ = 0: 3×2 + 4x + 1 = 0Дискриминант D = 16 − 12 = 4. Корни x_1,2 = −4 ± 2______  6, x₁ = −1/3; x₂ = −1.

Находим значения функции в этих точках и на краях отрезкаy(x) = x3 + 2×2 + x + 3;y(−4) = (−4)3 + 2(−4)2 − 4 + 3 = −64 + 2·16 − 4 + 3 = −33;y(−1/3) = (−1/3)3 + 2(−1/3)2 − 1/3 + 3 = −1/27 + 2·1/9 −1/3 + 3 = 223__27;y(−1) = (−1)3 + 2·(−1)2 − 1 + 3 = −1 + 2 − 1 + 3 = 3.

Выбираем самое большое из получившихся значений y. Это y(−1) = 3.

Ответ: 3

Задача 8

Найдите наибольшее значение функции на отрезке [−π/4; π/4].

Решение

На отрезке [−π/4; π/4] заданная функция определена и непрерывна (см. график tgx).

y’ = 36·_____  1cos2x − 36 + 0;

y’ не существует при cosx = 0, x_n = _π2·n, n Є Z. Ни одна из этих точек не входит в промежуток [−π/4; π/4].

y’ = 0 при cos2x = 1, cosx = ±1, x_k = πk, k Є Z. Отрезку [−π/4; π/4] принадлежит только точка x = 0.

Определяем значения функции в этой точке и на концах отрезка.y(x) = 36tgx − 36x + 9π + 7 y(0) = 36tg0 − 36·0 + 9π + 7 = 0 − 0 + 9π + 7 ≈ 9·3,14 + 7 = 35,26y(−π/4) = 36tg(−π/4) − 36·(−π/4) + 9π + 7 = 36·(−1) + 9π + 9π + 7 = −29 + 18π ≈ −29 + 18·3,14 = 27,52y(π/4) = 36tg(π/4) − 36·π/4 + 9π + 7 = 36·1 − 9π + 9π + 7 = 43.Самым большим из этих чисел является число 43.

Ответ: 43

Замечание: При дифференцировании не забудьте, что π — такая же константа, как любое другое число. Поэтому π’ = 0.

Задача 9

Найдите наибольшее значение функции на отрезке .

Решение

Функция определена и непрерывна при всех x > 0, в том числе и на отрезке .

y’ = 4x − 13 + 9·1_x + 0 = 4×2 − 13x + 9___________  x

y’ не существует при x = 0. Эта точка не входит в заданный промежуток. Не рассматриваем.

y’ = 0 при 4×2 − 13x + 9 = 0Решаем это квадратное уравнение через дискриминант, находим корни x₁ = 1, x₂ = 9/4 = 2,25.

x₁ = 1 является серединой заданного отрезка, x₂ = 2,25 не принадлежит отрезку. Значит нужно определить значения функции y(13/14), y(1) и y(15/14) и сравнить их между собой. Однако в данном случае вычисление значений y(13/14) и y(15/14) может оказаться слишком громоздким и с большой вероятностью привести к ошибкам. Проще вернуться к исследованию поведения производной в окрестности найденной точки экстремума.

y’ представляет собой дробь, знаменатель которой на отрезке [13/14;15/14] положителен. Значит знак производной на этом отрезке зависит только от числителя, т.е. определяется знаком квадратного трёхчлена 4×2 − 13x + 9. Графиком этого квадратного трёхчлена является парабола с ветвями, направленными вверх (4 > 0), пересекающая ось абсцисс в двух точках x₁ и x₂. Чертим «от руки» эскиз этого графика и видим, что левее корня x₁ квадратный трёхчлен, а значит и вся производная будут иметь знак «+», а правее — знак «−». Вывод: заданная в условии задачи функция на заданном отрезке левее x₁ = 1 возрастает, правее — убывает. Эта точка является точкой максимума внутри отрезка, значение функции в ней будет наибольшим.

Определяем егоy(x) = 2×2 − 13x + 9lnx + 8 y(1) = 2·12 − 13·1 + 9·ln1 + 8 = 2 − 13 + 9·0 + 8 = −3.

Ответ: −3

Задача 10

Найдите наименьшее значение функции на отрезке .

Решение

На отрезке функция определена и непрерывна (x = 0 не принадлежит отрезку).

y’ = (x2 + 25)’·x − x’·(x2 + 25)_____________________    (x)2 = (2x + 0)·x − 1·(x2 + 25)___________________     x2 = x2 − 25______    x2.

y’ не существует при x = 0. Эта точка не входит в заданный промежуток.

y’ = 0 при x2 − 25 = 0, x2 = 25, x = ±5.

x₁ = −5 не принадлежит отрезку , x₂ = 5 внутренняя точка отрезка.Находим значения функции

y(x) = x2 + 25______    x;

y(1) = 12 + 25______    1 = 26;

y(5) = 52 + 25______    5 = 10;

y(10) = 102 + 25_______    10 = 12,5.

Наименьшее значение y(5) = 10.

Ответ: 10

Вернуться и повторить другие задачи на производную.

1. Задачи на определение характеристик производной по графику функции.

Вернуться  к списку заданий первой части профильного уровня ЕГЭ по математке.

Производная по-простому

Где применяется

Немного о твоей будущей зарплате

Попробую объяснить несколько иначе, чем в школе.

Вы заканчиваете школу, поступаете в университет и начинаете подрабатывать:

В первый год после школы вы зарабатываете 0,5 у.е. (условных единиц). 

Вы хорошо учитесь, устраиваетесь по специальности или находите свое призвание, и ваши дела постепенно, но идут в гору!

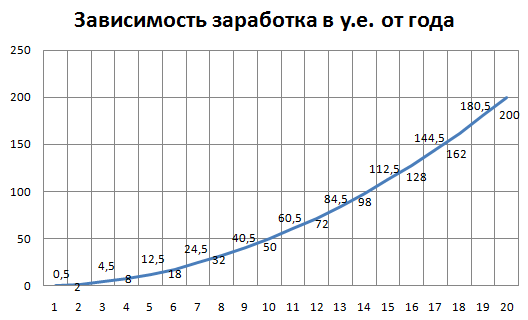
Какой молодец! Заработок растет не по годам, а по часам! 

Если посмотреть на этот график внимательнее, то можно увидеть сходство с ветвью параболлы, которая в самом простом случае задается уравнением y = x². Если это понятно, то дальше все проще!

Интересно, а на сколько увеличивался заработок из года в год:

I год: 0,5 − 0 = 0,5 .

II год: 2 − 0,5 = 1,5.

III год: 4,5 − 2 = 2,5.

IV год: 8 − 4,5 = 3,5.

…

Получается, что наш доход каждый год возрастал равномерно. Вот что выйдет, если построить график:

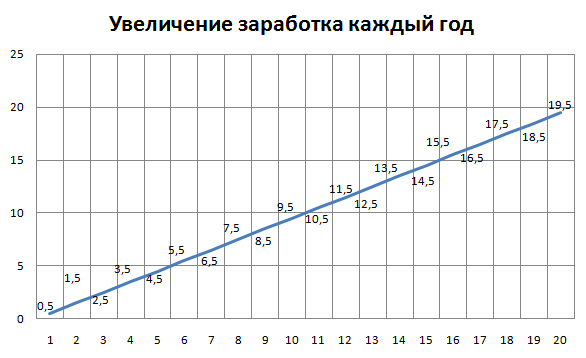
Получается прямая!

То есть все наши старания каждый год были постоянными, достаточно было ежегодно улучшать свой доход на 1 у.е.

Нетрудно заметить, что график заработка задается уравнением y = 0,5x².

А график увеличения заработка залается прямой y = x − 0,5.

Кто знает толк в производных, скажет Неверно!Конечно, производная от 0,5x² не будет равна x − 0,5, и это мы обсудим ближе к концу статьи.

Изменение заработка для нескольких лет

Для того, чтобы посчитать скорость изменения заработка, нужно взять один из «треугольников» с графика, например первый, и разделить длину вертикального катета (Δy) (в данном случае это 12,5 − 8 = 4,5) на длину горизонтального (Δx) (тут он равен 1).

Получится 4,5 / 1 = 4,5.

Таким образом, разделив вертикальный катет на горизонтальный, мы получаем скорость изменения функции, что показывает второй график.

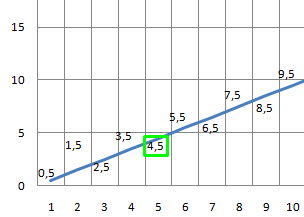
Но как же это все относится к производным?

А так, что производная показывает «скорость» изменения функции! 

Функция заработка предсталяет из себя график параболы (график функции) .

В тоже время функция увеличения заработка каждый год представляет прямую (график производной функции).

Однако прежде, чем ты расскажешь это своим друзьям, давай проверим, а если мы возьмем другой треугольник (в этот раз второй).

Вертикальный катет: 24,5 − 18 = 6,5.

Горизонтальный катет: 1.

Разделим: 6,5 / 1 = 6,5 — не сходится с первым треугольником!

А если объединить второй и третий треугольник?

Вертикальный катет: 40,5 − 18 = 22,5.

Горизонтальный катет: 9 − 6 = 3.

Разделим: 22,5 / 3 = 7,5 — опять не сходится!

Какая же тогда производная правильная?

Для того, чтобы верно найти производную, нужно взять как можно меньший горизонтальный катет — максимальное приближение (Δх)!

Сам график задается уравнением y = 0,5x².

Тогда возьмем x₁ = 4 => y₁ = 0,5 × 4² = 8, а при x₂ = 4,001 => y₂ = 0,5 × 4,001² ≈ 8,004.

Получается: Δy = 8,004 − 8 = 0,004,  Δх= 4,001 − 4 = 0,001.

Производная: Δy / Δх = 0,004 / 0,001 = 4.

И что же тогда производная?

Производная — это скорость изменения функции при самых маленьких значениях Δх (наименьших значениях горизонтального катета).

Именно поэтому производную и называют тангенсом (отношение противолежащего катета к прилежащему) угла наклона этой функции.

Если же мы посчитаем производную для каждой точки, получится такой график функции:

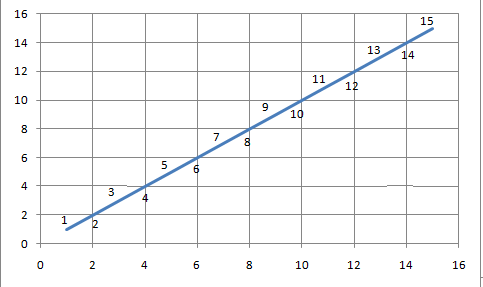
А это уже похоже на правду!

Производная от y = 0,5x² будет равна y = х (именно такой график получился у нас).

Погрешность в данном графике вызвана плохим приближением по оси х (в данном случае Δх = 1), из-за чего появляется неточность.

Конечно, можно не делать такое большое количество действий, проверяя точки.

Есть готовые формулы для базовых функций, пользуйтесь ими, если хотите облегчить себе жизнь.

Выводы:

1. Производные встречаются почти во всех областях: от медицины до финансов, по сути дела производная, показывая скорость изменения функции, предсказывает дальнейшее поведение функции.
2. Представьте матрешку, так же как в каждой матрешке внутри есть следующая, так и функция скрывает в себе производную. У каждой функции есть своя производная функции. Так же можно брать от производной функции еще одну производную и повторять действие до бесконечности. 
3. Производная функции показывает скорость изменения самой функции. Так же, как у вас есть родители и предки (предыдущии поколения), которые вам передали какие-то отличительные особенности, так и у функции есть производная, которая передает ей скорость ее изменения.

Будь в курсе новых статеек, видео и легкого математического юмора.

Производная в задачах с параметром

С помощью производной можно многое сказать о функции: где она возрастает или убывает, какие точки экстремума у нее есть, можно даже найти касательную к функции. Поэтому перед прочтением статьи рекомендуем ознакомиться с понятиями «Производная» и «Исследование функции с помощью производной». 

Вспомним несколько важных фактов, которые относятся к производной:

• производная положительна на участках возрастания функции;
• производная отрицательна на участках убывания функции;
• производная равна 0 в точках экстремума. 

Представим, что мы решили покататься на велосипеде по городу. Участки, на которых мы будем ехать в гору — это участки возрастания функции. Производная в них будет положительна: мы тратим много сил, чтобы подняться по склону вверх.

Остановимся на вершине, чтобы полюбоваться красивой панорамой. Это самая высокая точка горы— точка максимума, которая является экстремумом. 

Теперь спустимся с горы. Будем ли мы прикладывать силы? Нет, велосипед все сделает за нас. То есть производная отрицательна.

Скатившись с горы, мы попадем в самую низкую точку на рельефе, то есть в точку минимума. 

Чуть подробнее про точки минимума и максимума: 

• В точке минимума производная функции меняет знак с минуса на плюс. 
• В точке максимума производная функции меняет знак с плюса на минус. 

Рассмотрим, как эти знания могут пригодиться в решении задач с параметром. 

Как функция отражается в зеркале?Отражением функции в зеркале будет ни что иное, как производная. Именно она с точностью описывает поведение функции, ее характер и внешность. Поскольку графики функции и производной несколько отличаются друг от друга, то это будет скорее отражение в кривом зеркале, чем в обычном.

Производная функции может пригодиться вам при решении различных заданий из ЕГЭ по профильной математике. Например, частым гостем производная является в номерах 7 и 11. Помимо этого, она может помочь еще и при решении задания второй части №15 на оптимизацию.Сейчас мы потренируемся решать примеры с помощью производной.

Пример 1. При каких значениях параметра а наименьшее значение функции f(x) = x3 — 48x — a равно -133 на отрезке ?

Решение. 

Шаг 1. Для начала найдем производную функции. 

f'(x) = 3×2 — 48 = 3(x2 — 16) = 3(x — 4)(x + 4)

Тогда точки экстремума будут равны x = 4 и x = -4. В этих точках производная функции будет менять знак на противоположный.

Шаг 2. Определим, какая из получившихся точек будет точкой максимума, а какая точкой минимума. 

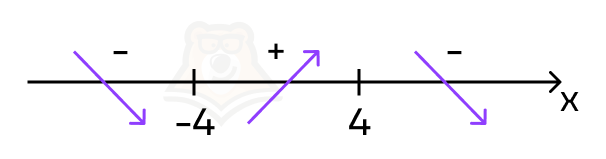
Как не запутаться в точках минимума и максимума при расстановке знаков на прямой?Можно показать стрелочками направление функции: на промежутках с минусом стрелочки смотрят вниз, а на положительных промежутках— вверх. Так мы условно показываем график функции, а значит, можем увидеть точки минимума и максимума визуально.

В точке «4» производная функции меняет знак с минуса на плюс, а значит, это точка минимума. 

В точке «-4» функция меняет знак с плюса на минус — это точка максимума.

Нас интересует значение функции на определенном отрезке, а именно от -2 до -5. Если мы отметим этот участок на прямой, то в него войдет только точка минимума.

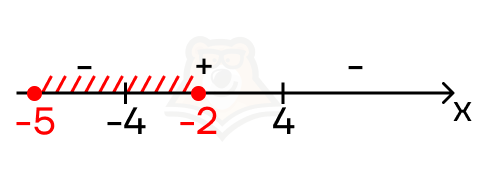
На минутку вспомним нашу поездку на велосипеде. 

Допустим, мы едем по получившейся числовой прямой, включив в точке —2  фитнес-браслет для контроля пульса. От точки —2 до точки 4 будет спуск с горы, а  от точки 4 до 5 будет подъем в гору. 

Браслет был слабо заряжен, и в точке 5 он сел. Мы не успели подняться до вершины горы с включенным браслетом.

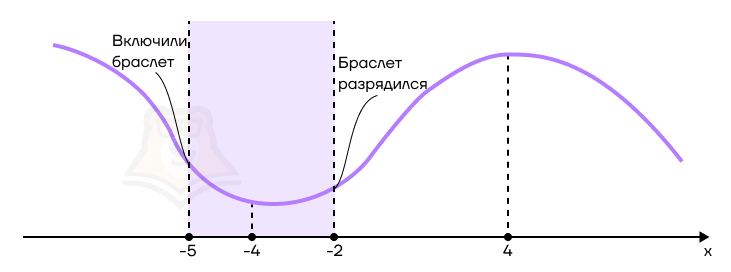
Вопрос: через какую самую низкую точку на маршруте мы проехали, пока работал фитнес-браслет? Через точку минимума, то есть 4. 

Рассмотрим эти же рассуждения на языке математики: до точки -4 функция возрастает, а от -4 до 4 убывает, после точки 4 снова возрастает. Если рассмотреть отрезок от -2 до 5, то от -2 до 4 функция убывает, от 4 до 5 функция возрастает. То есть в точке минимума функция точно будет принимать наименьшее значение. 

Шаг 3. Следовательно, \(f_наим=f(4)=4^3-48*4-a=64-192-a= -128-a\).

Шаг 4. По условию наименьшее значение функции должно быть –133, откуда 

-128-a= -133a=5

Ответ: 5

Достаточные условия существования экстремума

Первое условие. Если при переходе через точку производная дифференцируемой функции y = f(x) меняет свой знак с плюса на минус, то точка является точкой максимума, а если с минуса на плюс, то точкой минимума.

Действительно, если при и при то в промежутке функция f(x) возрастает, а в промежутке убывает, так что значение будет наибольшим в промежутке т.е. в точке функция имеет максимум. Аналогично доказывается случай для минимума функции. Графически сказанное поясняется на рис. 7.5.

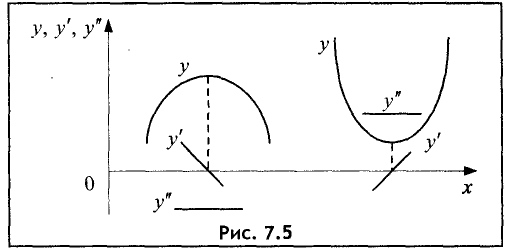
Если при переходе через точку производная не меняет своего знака, то в точке нет ни максимума, ни минимума (см. рис. 7.4).

Второе условие. Если функция y = f(x) дважды дифференцируема в точке , и ее первая производная в данной точке равна нулю, а вторая производная в этой точке положительна, то точка является точкой минимума. Если вторая производная функции y = f(x) отрицательна в точке , то она является точкой максимума.

Действительно, вторая производная вычисляется по формуле:

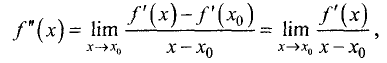
так как по условию.

Пусть Тогда дробь положительна для всех х из окрестности точки . Для знаменатель этой дроби поэтому а для знаменатель дроби Таким образом, производная при переходе точки меняет знак с минуса на плюс. Согласно первому условию в такой точке имеет место минимум. Аналогично можно показать, что при в точке имеет место максимум. Сказанное поясняется на рис. 7.5.

Если вторая производная в некоторой точке равна нулю, то эта точка также может быть экстремальной. Например, для функции в точке х = 0 имеет место минимум, хотя вторая производная в этой точке равна нулю. Действительно, и

Примеры задач

Задача 1

Исследовать на экстремумы функцию \(f(x)=x^3-3x^2.\)

Решение задачи по алгоритму:

1) \(D(y): x\in(-\infty;+\infty)\), т.е. x — любое число.

2) Производная: \(f'(x)=3x^2-6x\) .

3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:

Приравниваем f ‘(x) к 0, решаем квадратное уравнение \(3x^2-6x=0\), получаем \(x_1=0\),\(\;x_2=2.\)

4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала \((-\infty;0)\) в f'(x), например, пусть x = -1, тогда \(f'(x)=3{(-1)}^2-6(-1)=3+6=9\). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале \((2;+\infty)\) производная положительна, возрастает. Из этого следует, что x=0 — точка максимума, а x=2 — минимума.

5) Найдем значение экстремумов функции.

\(f(0)=0-3\times0=0\)

\(f(2)=2^3-3\times2^2=8-12=-4\)

Ответ: \(x_{min}=2,\;y_{min}=-4;\;x_{max}=0,\;y_{max}=0\) или (0;0) — минимум функции, (2;-4) — максимум.

Задача 2

Найти промежутки монотонности функции \(f(x)=\frac x{x^2-4}\).

1) \(D(y): x\in\mathbb{R},\;\)кроме\(\;\pm2\)

2) \(f'(x)=\frac{1(x^2-4)-x\times2x}{{(x^2-4)}^2}=-\frac{x^2+4}{{(x^2-4)}^2}\)

3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство \(-\frac{x^2+4}{{(x^2-4)}^2}\leq0\) и получим, что неравенство верно при любом x, значит функция убывает.

Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.

Ответ: f(x) убывает на промежутке \((-\infty;-2)\cup(-2;2)\cup(2;+\infty)\).

Задача 3

Докажите, что функция \(f(x)=x^5+2x^3-4\) возрастает на всех числовой прямой.

1) \(D(y): x\in\mathbb{R}\), значит критических точек нет.

2) \(f'(x)=5x^4+6x\)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках \((-\infty;0)\) и \((0;+\infty)\). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Дифференцируемость[]

См. также основную статью: Дифференцируемая функция

Производная f′(x){\displaystyle f'(x_0)} функции f{\displaystyle f} в точке x{\displaystyle x_0}, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f{\displaystyle f} является дифференцируемой в точке x{\displaystyle x_0} тогда и только тогда, когда её производная в этой точке существует и конечна:

(f∈D(x))⇔(∃f′(x)<∞).{\displaystyle \bigl( f \in \mathcal{D}(x_0) \bigr) \Leftrightarrow \bigl( \exists f'(x_0) < \infty\bigr).}

Для дифференцируемой в x{\displaystyle x_0} функции f{\displaystyle f} в окрестности U(x){\displaystyle U(x_0)} справедливо представление

f(x)=f(x)+f′(x)(x−x)+o(x−x){\displaystyle f(x) = f(x_0) + f'(x_0) (x-x_0) + o(x-x_0)}

Производная

Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями? 

Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции. 

Почему функции похожи на американские горки? Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.

Представим наши американские горки в виде функции. 

Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной. 

Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х). 

Отложим на нашем графике две точки: х и х₁ и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х₁;у₁). 

Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х₁ — х, а поднялся он на высоту у₁ — у. Для удобства дальнейших рассуждений примем эти расстояния за х и у. 

Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.

Теперь мы можем ввести определение приращения. 

Приращение функции — это разность между двумя значениями функции, то есть у.

Приращение аргумента — это разность между двумя значениями аргумента, то есть х.

Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению. 

Отсюда мы получаем определение производной функции. 

Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции. 

Производную функции обозначают как f'(x). 

\(f'(x) = \frac{\Delta y}{\Delta x}\: при\: \Delta x \rightarrow 0\)

Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках. 

Нахождение производной называется дифференцированием. 

Как с помощью производной оценить рост популярности видео в соцсети?Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати. Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр. В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени. Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);2) как изменилось время между этими точками (Δ времени);3) затем разделим Δ просмотров на Δ времени.Получается, что “производительность” нашего видео была 5 просмотров в час. Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:\(f'(x) = \frac{\Delta y}{\Delta x} = \frac{5}{1} = 5\)(просмотров в час)

Продолжаем искать производные вместе

Пример 12. Найти производную функции

.

Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим

.

Пример 13. Найти производную функции

Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим

Пример 14. Найти производную функции

Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:

Теперь вычислим производные в числителе и перед нами уже требуемый результат:

Пример 15.Найти производную функции

Шаг1. Применяем правило дифференцирования суммы:

Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):

Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:

и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя —
это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:

Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:

,

а производная, требуемая в условии задачи:

Ещё больше домашних заданий на нахождение производных

Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях «Производная произведения и частного функций» и
«Производная суммы дробей со степенями и корнями».

Также настоятельно рекомендуем изучить производную сложной функции.

Назад

Листать

Вперёд>>>

Поделиться с друзьями

Весь блок «Производная»

• Что такое производная
• Найти производную: алгоритмы и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Уравнение касательной и уравнение нормали к графику функции
• Правило Лопиталя
• Частные производные

Точки экстремума

Как уже было сказано ранее, производная функции может равняться 0. Она принимает такое значение в точках экстремума.

Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке. 

Точки экстремума — точки, в которых достигается экстремум. 

На рисунке видно, что точки А и В являются экстремумами. Например, до точки А функция будет возрастать, а после нее уже убывать, то есть наибольшее значение эта функция достигнет именно в точке экстремума. 

Если вспомнить наш вагончик, то в точке А он достигнет наибольшую высоту над землей. 

Во втором случае аналогичные рассуждения, но функция достигает уже наименьшее значение в точке В. 

В теме производной есть такие термины, как “точка минимума” и “точка максимума”. 

Точка минимума — это точка, в которой достигается минимальное значение функции.

В этой точке знак функции меняется с отрицательного на положительный (то есть сначала функция убывала, а потом начала возрастать). Это точка В. 

Точка максимума — это точка, в которой достигается максимальное значение функции на отрезке. 

В этой точке знак функции меняется с положительного на отрицательный (то есть сначала функция возрастала, а потом стала убывать). Это точка А. 

Также с точками экстремума связаны наибольшее и наименьшее значение функции. 

Важно!Следует вспомнить, что когда мы говорим о значении функции, то имеем в виду значение ординаты, то есть у (или f(x)). Наибольшее значение функции — точка на оси ординат, в которой достигается наибольшее значение функции на заданном отрезке. 

Наибольшее значение функции — точка на оси ординат, в которой достигается наибольшее значение функции на заданном отрезке. 

Например, в точке А будет достигаться наибольшее значение функции. 

Наименьшее значение функции — точка на оси ординат, в которой достигается наименьшее значение функции на заданном отрезке. 

В точке В будет достигаться наименьшее значение функции. 

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Как найти производную?

Пример 1

f(x) = 6x³

f′(x) = 3 * 6x²

f′(x) = 18x²

Степень от x спускается и из неё нужно вычесть 1.

Пример 2

f(x) = 3x³ – 5x² + 6x − 5

f'(x) = 3*3x² – 2*5x¹ + 6 − 0

f(x) = 9x² – 10x + 6

Пример 3

f(x) = (x−4) (2x+x²)

Нужно сначала раскрыть скобки:

f(x) = (x−4) (2x+x²)=

f(x) = 2x² − 8x + x³ − 4x²

f(x) = x³ − 2x² − 8x

Теперь можно приступать к поиску производной, как и в предыдущих примерах степень от x спускается и из неё нужно вычесть 1:

f´(x) = (x³ − 2x² − 8x)´=

f´(x) = 3x² − 2*2x¹ − 8 =

f´(x) = 3x² − 4x − 8

Пример 4

f(x) = √x

Переведём сначала корень в степень:

f(x) = x ^ (½)

Теперь можно производить вычисления производной с обычной формулой степеней:

f´(x) = ½ * x ^ (½ – 1)

f´(x) = ½ * x ^ (– ½)

f´(x) = ½ * (1/√x)

Можно остановиться здесь, но бывает, что ответ с корнем в знаменателе не считается совсем правильным, поэтому умножаем всю вторую дробь на «√x/√x».

(1/√x) * (√x/√x) = √x/x

Значит правильный и «красивый» ответ:

f´(x) = ½ * (√x/x)

Пример 5

f(x) = sin x − cos x

Из таблицы мы знаем:

(sin x)´ = cos x

(cos x)´ = − sin x

Так как это вычитание, осталось только подставить:

f´(x) = (sin x − cos x)´

f´(x) = cos x − (− sin x)

f´(x) = cos x + sin x

(u (v))´ = u´ (v) * v´

Пример

1. Сначала нужно разобраться, что «arctg x» является нашей простой (внутренней) частью функции, это наше “v” формулы.

2. Применяем формулу корня из таблицы в левой части, получится 1/2 √arctg x, оставляя правую нерешённой.

3. Применяем формулу arctg x из таблицы (1/ (1 + x²)).

4. Совмещаем и готово

4.1. Если хотите «красивый» ответ, нужно убрать корень из знаменателя, умножая всю эту дробь на √arctgx / √arctgx.

Получится √arctgx / (2 (1 + x²) arctgx)

План действий

Пример – дана функция f(x) на отрезке . Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку .
5. Вычислить значения функции на концах отрезка .
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

Алгоритм исследования функции на экстремум

1.Найти производную функции и приравнять ее нулю.

2.Решив это уравнение, определить подозрительные точки.

3.Исследовать знак производной слева и справа от каждой подозрительной точки и принять решение о наличии минимума или максимума.

4.Найти значения функции в экстремальных точках.

Пример:

Найти максимумы и минимумы функции

Решение:

Область определения функции — вся числовая ось. Определяем производную:

Подозрительные точки находим, решая уравнение

Отсюда 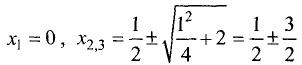или

Определяем вторую производную:

Для точки имеем у» = 18*0 —12*0 —12 = -12, т.е. в этой точке имеет место максимум. Его значение равно

у = 1,5*0-2*0-6*0 + 1 = 1.

Для точки имеем т.е. в этой точке имеет место минимум. Его значение равно

Для точки имеем т.е. в этой точке имеет место минимум. Его значение равно

Пример:

Решение:

Доход определяется разностью между выручкой за проданную продукцию 60х и ее себестоимостью, т.е.

Для определения оптимального объема выпуска найдем производную этой функции, приравняем ее нулю и решим полученное уравнение

Отрицательный корень не имеет экономического смысла, поэтому для дальнейших исследований принимаем Вторая производная в исследуемой точке r»(х) = -0,006х = -0,006 • 100 = -0,6 является отрицательной, т.е. в этой точке имеет место максимум функции. Таким образом, оптимальный объем выпуска равен 100 единицам продукции.

Доход, соответствующий оптимальному выпуску,

Для определения наибольшего и наименьшего значений на отрезке, помимо указанного алгоритма, находят значения функции на концах отрезка. Затем выбирают наибольшее и наименьшее значения из этих двух и всех экстремальных значений. Смысл сказанного поясняется на рис. 7.6.