Степень числа: определения, обозначение, примеры

Степень с иррациональным и действительным показателем

Известно, что множество действительных чисел можно рассматривать как объединение множеств рациональных и иррациональных чисел. Поэтому степень с действительным показателем можно будет считать определенной, когда будут определены степень с рациональным показателем и степень с иррациональным показателем. Про степень с рациональным показателем мы говорили в предыдущем пункте, осталось разобраться со степенью с иррациональным показателем.

К понятию степени числа a с иррациональным показателем будем подходить постепенно.

Пусть — последовательность десятичных приближений иррационального числа . Для примера возьмем иррациональное число , тогда можно принять , или , и т.п. Здесь стоит отметить, что числа — рациональные.

Последовательности рациональных чисел соответствует последовательность степеней , причем мы можем вычислить значения этих степеней на базе материала статьи . В качестве примера возьмем a=3, и , тогда , а после возведения в степень получаем .

Наконец, последовательность сходится к некоторому числу, которое и является значением степени числа a с иррациональным показателем . Вернемся к нашему примеру: степень с иррациональным показателем вида сходится к числу, которое с точностью до сотых равно 6,27.

Определение.

Степенью положительного числа a с иррациональным показателем называют выражение , значение которого равно пределу последовательности , где — последовательные десятичные приближения иррационального числа .

Степень числа нуль определяется для положительных иррациональных показателей, при этом . Например, . А степень числа с отрицательным иррациональным показателем не определяется, к примеру, — не определены.

Отдельно стоит сказать про иррациональную степень единицы – единица в любой иррациональной степени равна 1. Например, и .

Список литературы.

• Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
• Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
• Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Что означает возведение в степень

Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень.

К примеру, если стоит задача вычислить значение (0,4)^4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.

Куб числа

В выходной день бабушка пекла пирожки с малиной, клубникой и вишней. До прихода внуков она успела испечь по три пирожка с каждой начинкой. По рецепту пирожков должно получиться в три раза больше, чем выпеченных. Вычислите, сколько пирожков должно получиться по рецепту? 

Чтобы понять на сколько пирогов рассчитан рецепт бабушки, нужно знать, сколько пирогов бабуля успела испечь. Мы знаем, что готовы по три штуки с каждой начинкой – малина, клубника, вишня. Поэтому три готовых пирожка повторяем три раза, то есть: 3×3.

Зная сколько выпеченных изделий, можем найти, сколько пирогов получится согласно рецепту. Для этого, готовые пироги увеличиваем в три раза (умножаем на три):

3×3×3.

Мы видим, составляющая три использована три раза. Пользуясь изученным определением, можем записать иначе:  33

Составленное выражение произносится «три в кубе».

Вычислим: 

Бабушкин рецепт рассчитан на приготовление 27 пирожков.

Показатель степени числа равен 3, то говорят «число в кубе».

73 – семь в кубе;

93 – девять в кубе;

113 – одиннадцать в кубе.

Запомните:

Чтобы возвести число в куб, его нужно умножить само на себя три раза!

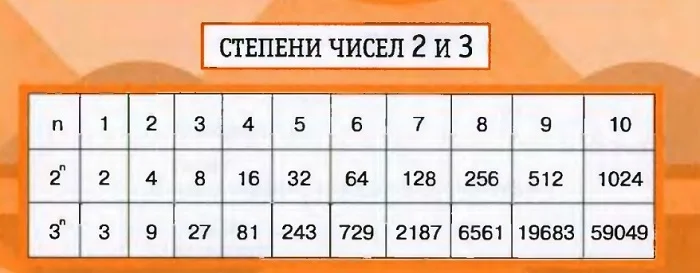
И в заключение урока рассмотрим таблицу, которая станет верным другом на протяжении учебного процесса.

Правила пользования таблицей!

На верхней горизонтальной строке записаны основания, в первом вертикальном столбце – показатели. Для нахождения нужного значения квадрата, куба числа, в верхней строке находим требуемое число и опускаемся на вторую, третью строку (зависит от показателя).

Вот и все! Благодаря табличке, не нужно выполнять вычисления, а просто держать её под рукой!

Интересные факты.

• 1) Человеческий мозг содержит 2×1010 нервных клеток, имеет ежедневную возможность сохранять 8,6×107  бит различной информации. У взрослых людей память хранит множество информации –  1018 бит.
• 2) Ежесекундно человеческий мозг выполняет 105 химических процессов. Сплетение нейронов головного мозга в 1,4×103  раз сложнее, всей мировой сети телефонной связи.
• 3) Все человечество на планете можно поместить в куб, имеющий длину ребра 1 километр.
• 4) Самое маленькое число, состоящее из четырех знаков и являющееся суммой двух кубов натуральных чисел.
• 5) В древние времена славяне использовали своеобразную запись чисел,  большого значения.

103 называли «тысяща»;

106 имело название «тьма»

1012 прозвали «легион»

1024 называлось «леодр»

1048 читалось «ворон»

1049 произносили, «колода»

Степень с целым показателем

После того как мы определили степень числа a с натуральным показателем, возникает логичное стремление расширить понятие степени и перейти к степени числа, показателем которой будет любое целое число, в том числе и отрицательное и нуль. Это следует делать так, чтобы оставались справедливыми все свойства степени с натуральным показателем, так как натуральные числа являются частью целых чисел.

Степень числа a с целым положительным показателем есть не что иное как степень числа a с натуральным показателем: , где n — целое положительное число.

Теперь определим нулевую степень числа a. Будем исходить из свойства частного степеней с одинаковыми основаниями: для натуральных чисел m и n, m<n и отличного от нуля действительного числа a выполняется равенство am:an=am−n (условие a≠0 необходимо, так как в противном случае мы бы имели деление на нуль). При m=n записанное равенство нас приводит к следующему результату an:an=an−n=a. Но с другой стороны an:an=1 как частное равных чисел an и an. Следовательно, приходится принять a=1 для любого отличного от нуля действительного числа a.

А как же быть с нулем в нулевой степени? Подход, примененный в предыдущем абзаце, не подходит для этого случая. Можно вспомнить про свойство произведения степеней с одинаковыми основаниями am·an=am+n, в частности при n=0 имеем am·a=am (из этого равенства тоже видно, что a=1). Однако, при a=0 мы получим равенство 0m·0=0m, которое можно переписать как 0=0, оно верно при любом натуральном m вне зависимости от того, чему равно значение выражения 0. Иными словами, 0 может быть равно любому числу. Чтобы избежать этой многозначности, не будем приписывать нулю в степени нуль никакого смысла (по этим же соображениям при изучении деления мы не стали придавать смысл выражению 0:0).

Несложно проверить, что принятое нами равенство a=1 для отличных от нуля чисел a согласуется со свойством степени в степени (am)n=am·n. Действительно, при n=0 имеем (am)=1 и am·0=a=1, а при m=0 имеем (a)n=1n=1 и a0·n=a=1.

Так мы пришли к определению степени с нулевым показателем. Степень числа a с нулевым показателем (a отличное от нуля действительное число) равна единице, то есть, a=1 при a≠0.

Приведем примеры: 5=1, (33,3)=1, , а 0 – не определено.

Нулевую степень числа a определили, осталось определить целую отрицательную степень числа a. В этом нам поможет все то же свойство произведения степеней с одинаковыми основаниями am·an=am+n. Примем m=−n, что требует условия a≠0, тогда a−n·an=a−n+n=a=1, откуда заключаем, что an и a−n – взаимно обратные числа. Таким образом, логично определить число a в целой отрицательной степени −n как дробь . Несложно проверить, что при таком задании степени отличного от нуля числа a с целым отрицательным показателем остаются справедливыми все свойства степени с натуральным показателем (смотрите ), к чему мы и стремились.

Озвучим определение степени с целым отрицательным показателем. Степень числа a с целым отрицательным показателем −n (a отличное от нуля действительное число) – это есть дробь , то есть, при a≠0 и натуральном n.

Рассмотрим данное определение степени с целым отрицательным показателем на конкретных примерах: .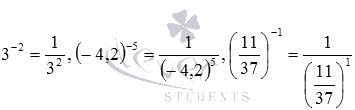

Подытожим информацию этого пункта.

Определение.

Степень числа a с целым показателем z определяется так:

Основание и показатель

 Математика – точная наука. Каждый компонент имеет определенное наименование, определенное место. Давайте вспомним наименования составляющих в различных математических действиях:

У изученного действия, составляющие имеют свои отличные от других наименования. Их называют: основание и показатель.

Запишем правильную формулировку для составляющих рассмотренного действия.

Числовое значение дублирующейся составляющей, называют основанием степени.

Цифра, стоящая справа, обозначает, численность повторяющихся множителей,называется показателем степени

В выражении 89, основанием является 8, а показателем 9. Значит, чтобы найти значение рассматриваемого выражения, нужно умножить число 8 само на себя 9 раз.

Найдем значение выражения 55.

Для верного проведения необходимых вычислений определим основание   (дублирующийся компонент) — пять, и показатель (численность составляющих)  – пять.

Имеем:

Исходя из рассмотренных примеров, можно сделать вывод как возвести число в степень:

для возведения числа в степень достаточно это число умножить само на себя несколько раз (на численность повторов указывает показатель степени).

Вычислим: 26

Нам необходимо возвести два в шестую степень. Главное – нужно умножить  два, само на себя шесть раз:

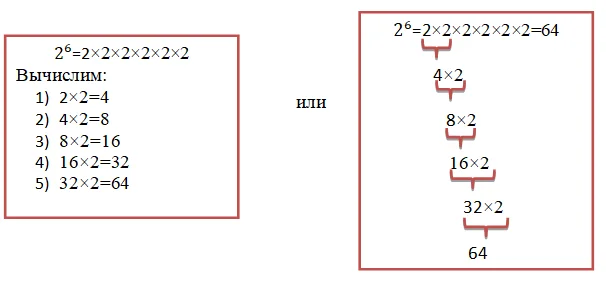
Получается, 26=64

Все очень просто! Главное – запомнить, что для возведения числа в степень, нужно умножить его само на себя, а сколько раз это сделать, вам подскажет показатель!

Квадрат и куб числа.

Как запомнить?

Заучить первый ряд и второй, остальные — по желанию или по нужде. Но придется именно запомнить до такой степени, чтобы эта информация у тебя была на одном уровне с таблицей умножения. Нарешивать, конечно, тоже можно, но уж лучше решать задачки или выражения, когда у тебя есть четкое понимание основ. Хотя, если будешь решать задачки, где в условии постоянно будут степени, то со временем ты устанешь смотреть в табличку каждый раз, и твой мозг решит, что пора запомнить эту информацию. А если тебе скучно, то можешь каждый раз прорешивать каждую степень, — тоже со временем запомнишь до такого состояния, что тебе будет во сне мерещиться.

Что такое нулевая степень числа?

Нулевая степень числа — это особый случай, когда возводимое в степень равно одному. В математике обычно соглашаются, что:

• любое число возводимое в нулевую степень будет равно единице: a0 = 1;
• ноль возводимый в нулевую степень находится в неопределенном состоянии;
• любое отрицательное число, возводимое в нулевую степень, дает также единицу.

Это свойство нулевой степени числа особенно важно в алгебре и геометрии. Например, в теореме Пифагора о треугольнике, где один из катетов равен нулю, мы можем возвести этот катет в степень и получить единицу, что позволяет нам вычислить длину гипотенузы треугольника

Также, в экономике упрощение выражений с помощью нулевой степени числа дает возможность определить единичные коэффициенты признаков. Это помогает сократить время при анализе данных и построении моделей.

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

• an * am = (a)(n+m),
• an : am = (a)(n-m),
• (ab ) m=(a)(b*m).

Проверим на примерах:

23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично: 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.

(23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

33 + 24 = 27 + 16 = 43, 52 – 32 = 25 – 9 = 16

Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4

А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.

Как производить вычисления в более сложных случаях? Порядок тот же:

• при наличии скобок – начинать нужно с них,
• затем возведение в степень,
• потом выполнять действия умножения, деления,
• после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

1. Корень n-ой степени из числа a в степени m запишется в виде: am/n.
2. При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
3. При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
4. При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
5. Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
6. Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Степень с целым показателем

Определение 2

Степенью с целым показателем называется степень, показателем которой является любое целое число. Это своего рода расширение множества чисел с натуральным показателем.  К последним прибавляются числа с отрицательным значением и ноль.

Рассмотрим степень с целым отрицательным n. Любое число вида a-n можно представить в виде 1/an. При этом a не должно быть равно нулю. n может быть любым натуральным числом.

Примеры 17 — 18

7-5 не является степенью с натуральным показателем, но в то же самое время является степенью с целым показателем. Примечательно, что равное ему число (1/7)5 будет степенью с целым n. Мы рассматриваем 7-5 и (1/7)5, как равные, но, всё-таки, разные числа.

(4/5)-1 можно представить как 1/(4/5)1.

Сложнее дело обстоит с понятием нулевой степени. Чтобы её объяснить, ещё раз приведём правило по делению степеней с равными основаниями.

Правило 1

Равенство am/an = am-n остаётся верным лишь в том случае, когда m и n будут натуральными числами, m < n и a не равно нулю. Последнее условие позволяет нам избежать деления на нуль. Если m и n окажутся равными, то мы придём к результату (an/an) = an-n = a

Т. е. при делении степеней, которые имеют одно и тоже основание из показателя делимого следует вычесть n делителя. В случае, когда и они одинаковы, например, если a3 разделить на a3, мы получим a.

Как известно из курса элементарной математики, частное от деления любого числа на самого себя всегда равно единице. Из этого напрямую следует, что нулевая степень любого числа всегда равна 1.

Пример 19

7= 1, -5= 1, (3/5) = 1, (√8) = 1, (7567776) = 1.

Несколько неожиданным для многих является тот факт, что ноль в степени ноль тоже равен единице 0 = 1. Положение осложняет тот факт, что на ноль делить нельзя. Так откуда же тогда взяли, что нулевая степень нуля есть 1.

На самом деле, хотя на ноль никакое число не делится, оно может делится на сколь угодно малое, т. е. близкое к нулю число. В высшей математике доказывается, что предел (a/a), когда a является бесконечно малой величиной, действительно стремится к 1.

Свойства степени с целым показателем практически ничем не отличаются от её свойств с натуральным. Нужно только помнить, что в показателе появляются отрицательные числа и их следует складывать и вычитать по строго определённым для этого правилам.

Примеры 20 — 21

57* 5-3= 57-3 = 54.

84/8-2 = 84-(-2)= 86.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

3.4. Степени и корни

Для того, чтобы возвести число в степень с натуральным показателем , нужно умножить число само на себя раз:

В этой записи – основание, – показатель степень.

Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных).

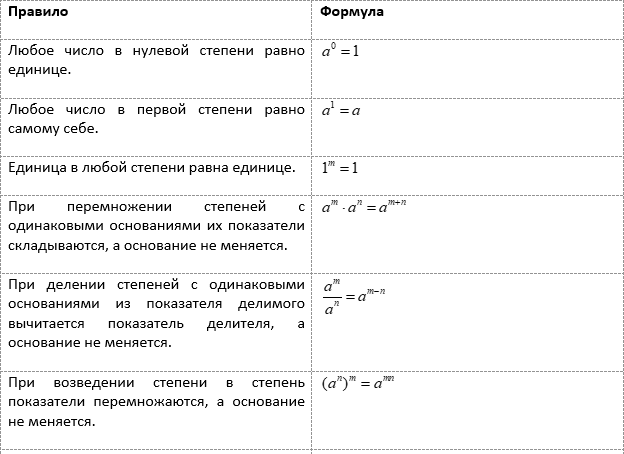
Применим эти правила для решения следующих задач.

Пример 1

Воспользуемся формулой для частного степеней с одинаковыми основаниями.

Пример 2

Так как степень частного равна частному степеней, занесем всю дробь под одну степень.

Пример 3

Для удобства представим и занесем всю дробь под одну степень.

Иногда для записи дробных степеней используют специальный знак – корень. На самом деле корень — всего лишь дробная степень:

Чаще всего встречается квадратный корень из числа:

Выражения с корнями преобразуется по тем же правилам, что и все остальные степени.

Следует различать корни нечетной степени и корни четной степени .

Корень нечетной степени из отрицательного числа – отрицательное число; из положительного – положительное.

Корень четной степени берется только из неотрицательного числа. Само значение корня четной степени может быть только неотрицательным.

.

Пример 4

, следовательно, корень из этого выражения существует. При этом значение может быть любым. Если действовать по правилам степеней без модуля, имеем:

.

В случае отрицательного получаем, что корень четной степени равен отрицательному числу, что невозможно.

Пример 5

Так как корень – это степень, то можем воспользоваться правилом «степень произведения равна произведению степеней».

Пример 6

Частное степеней равно степени частного, поэтому занесем всю дробь под общий корень.

Пример 7

Представим число в виде произведения, чтобы можно было воспользоваться правилом «При возведении степени в степень показатели перемножаются, а основание не меняется» в обратную сторону.

Помимо выражений с числами, в заданиях часто встречаются выражения с символьными переменными. К счастью, выписанные нами формулы, продолжают работать и в этом случае.

Пример 8

Возведем степень в степень, перемножая показатели. Так как все основания одинаковые, то заменим произведение степеней на сумму показателей, а частное – на разность. Основание при этом не меняем.

Пример 9

Перепишем корень как дробный показатель. Заменим возведение степени в степень на произведение показателей. Затем преобразуем произведение степеней, сложив их показатели.

Прочитано
Отметь, если полностью прочитал текст

Степень числа с иррациональным показателем

Чтобы разобраться в этом вопросе, нужно разобраться в том, что является иррациональным числом. Любое рациональное число допускает его представление в виде бесконечной периодической десятичной дроби либо как обыкновенную дробь типа (m/n). Об иррациональных числах этого не скажешь. Десятичные дроби, с помощью которых выражаются иррациональные числа, бесконечны и апериодичны. Примерами иррациональных чисел являются √7, число \, √2 + √3.

Строится степень с рациональным n с помощью так называемого предельного перехода по последовательностям степеней с рациональными показателями. Они с недостатком либо с избытком приближаются к степени иррациональным n.

Покажем как это происходит. Пусть нам дано иррациональное число a.

a0 = 1,6 , a1 = 1,67, a2 = 1,671…

a0 = 1,67, a1 = 1,6717, a2 = 1,671753…

И т. д. Заметьте – сами приближения, это рациональные числа.

Последовательности приближений нам нужно поставить в соответствие последовательность степеней αa, αa1, αa2. Значения этих степеней можно подсчитать.

a = 1,67175331. Пусть для примера у нас будет α = 3

Тогда получается αa = 3,167; αa1 = 3,16717; αa2= 3,1671753 и т. д.

Указанная последовательность сводится к числу, которое окажется значением степени с основанием α и иррациональным показателем a. После некоторой работы в итоге получаем 31,67175331 = 6,27.

Свойства у степени с иррациональным n в целом такие же, как рациональным. В частности, сложение показателей при перемножении, сравнение иррациональных степеней происходят аналогичным образом. Нужно только иметь в виду, что при бесконечности и апериодичности иррациональной дроби вы имеете дело с приближёнными с той или иной точностью значениями. Впрочем, в зависимости от поставленной задачи, нужной точности достичь можно в любом случае. Очень осторожны будьте с приближениями. У новичков здесь очень часто случаются ошибки. После некоторого опыта и практики действия совершаются автоматически. Старайтесь на первых порах порешать как можно больше примеров. Пусть они кажутся вам однотипным, но навык отточить и закрепить позволяют.