Все об окружности на егэ и огэ

Окружность, описанная вокруг прямоугольного треугольника

Эту теорему многие забывают. А зря, ведь некоторые задачи B8 без нее вообще не решаются. Точнее, решаются, но с таким объемом вычислений, что вы скорее уснете, чем дойдете до ответа.

Что следует из этой теоремы?

1. Середина гипотенузы равноудалена от всех вершин треугольника. Это прямое следствие теоремы;
2. Медиана, проведенная к гипотенузе, делит исходный треугольник на два равнобедренных. Как раз это и требуется для решения задачи B8.

Поскольку угол равен 90°, треугольник — прямоугольный. Получается, что — медиана, проведенная к гипотенузе. Значит, треугольники и — равнобедренные.

В частности, рассмотрим треугольник . В нем = . Но в равнобедренном треугольнике углы при основании равны — см. «Задача B8: отрезки и углы в треугольниках». Поэтому искомый угол = .

Итак, осталось выяснить, чему равен угол . Для этого снова обратимся к исходному треугольнику . Обозначим угол = . Поскольку сумма углов в любом треугольнике равна 180°, имеем:

Разумеется, последнюю задачу можно решить по-другому. Например, легко доказать, что треугольник — не просто равнобедренный, а равносторонний. Значит, угол равен 60 градусов. Отсюда угол равен 90 − 60 = 30 градусов. Как видите, можно использовать разные равнобедренные треугольники, но ответ всегда будет один и тот же.

1. Задача B8: отрезки и углы в треугольниках
2. Работа с формулами в задаче B12
3. Тест к уроку «Округление с избытком и недостатком» (1 вариант)
4. Метод интервалов: случай нестрогих неравенств
5. Вебинар по заданию 13: тригонометрия
6. Производительность совместного труда

Теорема о вписанном угле

Теорема 1

Градусная мера вписанного угла равняется половине градусной меры дуги, на которую он опирается.

Доказательство.

Пусть нам дана окружность с центром в точке $O$. Обозначим вписанный угол $ACB$ (рис. 2). Возможны три следующих случая:

Луч $CO$ совпадает с какой либо стороной угла. Пусть это будет сторона $CB$ (рис. 3).

Рисунок 3.

В этом случае дуга $AB$ меньше ${180}^{{}^\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:

Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).

Рисунок 4.

Получаем

Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).

Рисунок 5.

Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим

Получаем

Теорема доказана.

Приведем следствия
из данной теоремы.

Следствие 1:
Вписанные углы, которые опираются на одну и туже дугу равны между собой.

Следствие 2:
Вписанный угол, который опирается на диаметр — прямой.

Измерения дуг и углов.

Длина окружности. Дуги и углы измеряются в градусах и радианах. Сперва о градусах. Для углов проблем нет — нужно научиться измерить дугу в градусах.

Градусная мера (величина дуги) — это величина (в градусах) соответствующего центрального угла

Что здесь значит слово «соответствующего»? Смотрим внимательно:

Видишь две дуги и два центральных угла? Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше), а меньшей дуге соответствует меньший угол.

Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.

А теперь о страшном — о радианах!

Что же это за зверь такой «радиан»?

Представь себе: радианы — это способ измерения угла … в радиусах!

Угол величиной радиан — такой центральный угол, длина дуги которого равна радиусу окружности.

Тогда возникает вопрос — а сколько же радиан в развёрнутом угле?

Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?

Этим вопросом задавались учёные ещё в Древней Греции.

И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде и т.п.

И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в раза или в раз больше радиуса! Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву.

Итак, — это число, выражающее отношение длины полуокружности к радиусу.

Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём радиан. Именно оттого, что половина окружности в раз больше радиуса.

Древние (и не очень) люди на протяжении веков (!)
попытались поточнее подсчитать это загадочное число, получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы — нам достаточно двух знаков после занятой, мы привыкли, что

Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна, а точно эту длину просто невозможно записать «человеческим» числом — нужна буква. И тогда эта длина окружности окажется равной. И конечно, длина окружности радиуса равна.

Вернёмся к радианам.

Мы выяснили уже, что в развёрнутом угле содержится радиан.

Что имеем:

Значит, рад., то есть рад. Таким же образом получается табличка с наиболее популярными углами.

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

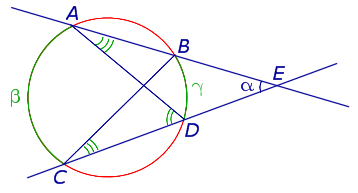
Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

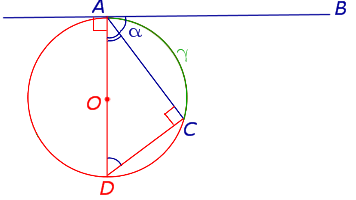
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

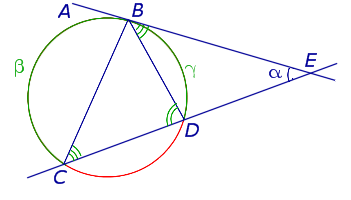
Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

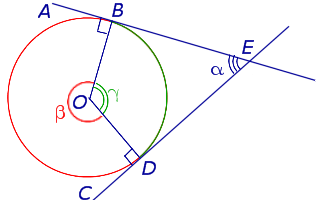
Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы образованные при пересечении двух прямых

При пересечении двух прямых образуются два вида углов:

• смежные;
• вертикальные.

Смежные углы

Определение

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.

Свойства смежных углов

1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Вертикальные углы

Определение

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Пример:

Пары углов 1 и 3; 2 и 4 – являются вертикальными

По свойству вертикальных углов:

\

\

Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными

По свойству смежных углов:

\

\

\

\

Смежные углы	Вертикальные углы
Два угла с общей стороной и вершиной называются смежными.	Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами.
Имеют общую сторону и общую вершину.	Имеют общую вершину, но не имеют общую сторону
Смежные углы не всегда равны по величине	Вертикально противоположные углы равны по величине

Разница между смежными и вертикальными углами

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной
к окружности, а их общая точка называется точкой касания прямой
и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в
   точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны
и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые
   ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит
   пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке
M, то произведение отрезков одной хорды равно произведению отрезков
другой хорды: AM•MB = CM•MD.

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения
  ,
  ее радиус r вычисляется по формуле:

r = ,

где S — площадь треугольника, а —
полупериметр;

центр описанной окружности — точка пересечения
,
ее радиус Rвычисляется по формуле:

R =
,

R = ;

здесь a, b, c — стороны треугольника,
— угол, лежащий против стороны a, S — площадь треугольника;

центр описанной около окружности лежит на середине ;

центр описанной и вписанной окружностей треугольника совпадают только
в том случае, когда этот треугольник — .

Окружность и четырехугольники

• около
  можно описать окружность тогда и только тогда, когда сумма его внутренних
  противоположных углов равна 180°:

 +
 =  +
 = 180°;

в можно вписать
окружность тогда и только тогда, когда у него равны суммы противоположных
сторон:

a
+ c = b + d;

• около можно
  описать окружность тогда и только тогда, когда он является ;
• около
  можно описать окружность тогда и только тогда, когда эта
  — ; центр
  окружности лежит на пересечении оси симметрии
  с
  к боковой стороне;
• в можно вписать
  окружность тогда и только тогда, когда он является .

Определения и свойства окружности

Введем несколько определений, связанных с темой окружности. Данные термины можно встретить на уроках в седьмом классе и других курсах по алгебре и геометрии.

1 Примечание 1

В распространенных случаях возникает путаница в понятиях окружности и круга. Заметим, что кругом может называться множество точек на плоскости, которые при построении ограничены окружностью, то есть данные точки расположены во внутренней области окружности.

Окружность обладает рядом свойств:

1. Если три точки на плоскости не принадлежат общей прямой, то через них допустимо построить единственную окружность.
2. Точка (С), в которой касаются две окружности, расположена на общей с центрами этих окружностей прямой (АВ).
3. Изопериметрическое неравенство: из всех замкнутых кривых на графике, имеющих одинаковую длину, окружность ограничивает область с максимальной площадью.

При решении самостоятельных работ и задач на некоторые окружности пригодятся следующие формулы, чтобы находить ключевые параметры:

Диаметр окружности можно высчитать таким образом:

Длина окружности в теории:

Радиус окружности можно узнать с помощью формулы:

Краткие правила пользования тригонометрической окружностью

• Углы, отсчитываемые против часовой стрелки, положительны, по часовой – отрицательны;
• Каждой точке на окружности соответствует бесконечное количество углов с периодом \(360^o\) или \(2\pi\);
• Координата по \(x\) любой точки на окружности – это значение косинуса угла, координата по \(y\) – синуса;
• Значения косинуса и синуса принадлежат промежутку \(\);
• Синус положительный в первой и второй четвертях, отрицательный – в третьей и четвертой;
• Косинус положительный в первой и четвертой, отрицательный – во второй и третьей;
• Чтобы найти тангенс угла, нужно нарисовать ось тангенса параллельно оси \(y\). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью тангенса. Координата полученной точки на оси тангенса и будет значением тангенса угла;
• Чтобы найти котангенс угла, нужно нарисовать ось котангенса параллельно оси \(x\). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью котангенса. Координата полученной точки на оси котангенса и будет значением котангенса угла;
• Тангенс и котангенс положительны в первой и третьей четвертях, отрицательны – во второй и четвертой;
• Тангенс и котангенс могут принимать значения из промежутка \((-\infty;+\infty)\).

Касательная, хорда, секущая к окружности

Касательная

Касательная имеет с окружностью только одну общую точку. Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.а — касательная,А — точка касания,ОА — радиус окружности,a┴OA

Отрезки касательных

Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
а, b  — касательные,

ВС=СА,

∠ВСО=∠ОСА

Угол между касательной и хордой

Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.
а — касательная,А — точка касания,ВА — хорда,∠ВАС= половине градусной меры дуги АВ.

Свойство касательной и секущей

Если через точку, лежащую вне круга провести касательную и секущую, то квадрат длины отрезка касательной равен произведению длин отрезков секущей и ее внешней части.
а — касательная,А — точка касания,CD — секущая,
СА2=СВ*СD.

Свойство хорд

Если хорды пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.
CF, AB — хорды,

CK*KF=AK*KB

Свойство секущих

Если через точку, лежащую вне круга провести две секущие, то произведение длин секущей и ее внешней части одной секущей равно произведению длин секущей и ее внешней части другой секущей.CD, CF — секущие,CD*CB=CF*CA.

Длина окружности. Длина дуги

Длина вычисляется по формуле: С=2πR.
Длина дуги вычисляется по формуле: l=C*α:360 или l=πRα:180. α — градусная мера дуги.

Площадь круга. Площадь сектора. Площадь сегмента

OFB — секторKCA — сегментПлощадь круга вычисляется по формуле: S=πR2.
Площадь сектора вычисляется по формуле: S=πR2 *α : 360.

Площадь сегмента находят как разность площадей сектора и треугольника: S=S сектора КОС — S треугольника КОС.

Описанные многоугольники

В любой треугольник можно вписать единственную окружность. Центр окружности — точка пересечения биссектрис треугольника.

Если в прямоугольный треугольник вписать окружность, то радиус можно найти по формуле: r=(a+b-c):2, где a,b — катеты, с- гипотенуза треугольника.

Если в четырехугольник можно вписать окружность, то суммы длин его противолежащих сторон равны.

a+b=c+d
Площадь описанного многоугольника: S=p*r, где р — полупериметр многоугольника, r — радиус окружности.

Вписанные многоугольники

Около любого треугольника можно описать единственную окружность. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Радиус описанной окружности можно найти по формуле: 2R=a: sin α, где а — сторона треугольника и α — противолежащий ей угол. В прямоугольном треугольнике R=c:2, где с — гипотенуза.

Если около четырехугольника описана окружность, то суммы градусных мер противолежащих углов  равны 180°.∠А+∠С=∠В+∠D=180°

Вписанные углы

Вокруг любого угла можно описать окружность. Он бывает центральным или вписанным. Термины нужно различать между собой, чтобы правильно применять следствия из утверждения. Центральным называется произвольный угол, у которого вершина совпадает с центральной точкой окружности, а его стороны эквивалентны радиусам. Вписанным является любой угол с вершиной, расположенной на окружности и сторонами, пересекающими ее.

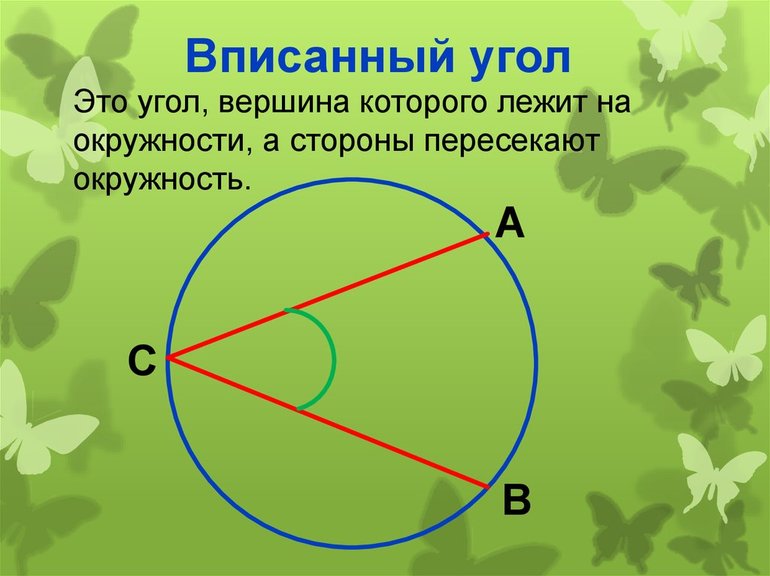
Затем следует рассмотреть теоремы о вписанных углах. Кроме того, центральный также является вписанным, но отличие состоит в том, что его вершина совпадает с центром круга. На основании утверждений можно сформулировать некоторые свойства вписанного угла. Последние могут также оказаться полезными при вычислении параметров некоторых фигур.

Основные теоремы

Теоремы применяются для оптимизации вычислений некоторых величин и параметров фигур, образованных углами и описанной окружностью вокруг них. Необходимо отметить, что специалисты классифицируют их на два вида: для вписанных и углов, образованных хордами и касательными. В первом случае утверждения, которые следует доказать, являются следующими:

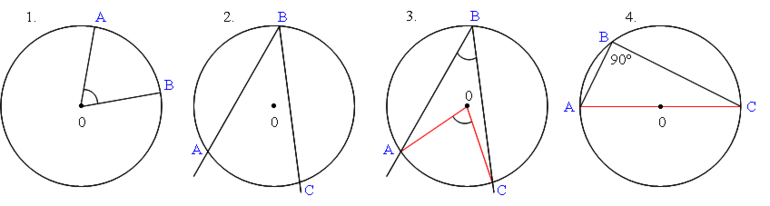
1. Градусная мера вписанного угла в некоторую окружность равна половине центрального, опирающегося с ним на одну дугу.
2. Если два угла опираются на одну дугу, то они конгруэнтны.
3. Когда углы опираются на одну хорду и лежат по одну сторону от нее, тогда их градусные меры равны между собой.
4. Сумма углов эквивалентна 180 градусам, когда их вершины лежат по разные стороны от общей хорды.
5. Если некоторый угол опирается на диаметр, то он соответствует 90 градусам, т. е. является прямым.
6. Средняя точка гипотенузы прямоугольного треугольника совпадает с центром окружности, описанной вокруг него.
7. Угол, который опирается на дугу, равен ½ от ее градусной меры.

Необходимо отметить, что вышеописанные теоремы являются также и свойствами. Следует ввести обозначение вписанного ∠ АВС. В первом случае свойство доказывается для двух вариантов. Первый — ∠ АВС лежит на диаметре АВ. Необходимо обозначит центральный ∠ АОС. Следовательно, АО = ВО = R. Треугольник АОВ является равнобедренным, а его ∠ при основании равны (∠ АВО = ∠В АО). Для внешнего ∠ АОС справедливо такое равенство: ∠ АОС = 2 * ∠В АО. Если центральная точка круга лежит внутри ∠ABC. Следует провести биссектрису вписанного ∠, пересекающую окружность в точке D. Тогда ∠ABC = ∠AОC / 2.

Другие случаи

Однако бывают и другие случаи, в результате которых образовываются углы внутри окружности. Специалисты выделяют следующие теоремы о них, образованных касательными и хордами:

1. Размерность угла, который образован при пересечении хорд, эквивалентна ½ от суммы размеров его дуг. Углы между собой равны, поскольку являются вертикальными.
2. Если существуют две секущие, которые пересекаются за пределами окружности, то угол равен ½ от разности соответствующих дуг.
3. Когда проведена касательная и хорда к общей точке окружности, тогда градусная мера эквивалентна половине дуги, образованной данными элементами.
4. Угол, образованный секущей и касательной, эквивалентен ½ разности образованных при этом дуг.
5. Если угол образуют две касательные к заданной окружности, то его размерность соответствует ½ от разности дуг между сторонами первого.

Типы заданий по СтатГраду с краткими ответами

Касательная, хорда, секущая, радиус

1. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, BC = 72. Найдите AK .

Ответ:

15

2. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 8, BC = 24. Найдите AK .

Ответ:

16

3. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 5, BC =15. Найдите AK.

Ответ:

10

4. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, BC =16. Найдите AK.

Ответ:

6

5. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.

Ответ:

36

6. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ:

46

7. На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.

Ответ:

28

8. На окружности отмечены точки A и B так, что меньшая дуга AB равна 152° . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ:

76

Центральные и вписанные углы

9. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 113°. Ответ дайте в градусах.

Ответ:

56,5

10. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.

Ответ:

29,5

11. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 167°. Ответ дайте в градусах.

Ответ:

83,5

12. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах.

Ответ:

23,5

13. В угол C величиной 157° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

23

14. В угол C величиной 18° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

162

15. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

97

16. В угол C величиной 133° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ:

47

Окружность, описанная вокруг многоугольника

17. Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.

Ответ:

9

18. Радиус окружности, описанной около равностороннего треугольника, равен 18. Найдите высоту этого треугольника.

Ответ:

27

19. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:

148

20. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:

99

21. Радиус окружности, описанной около квадрата, равен 16√2 . Найдите длину стороны этого квадрата.

Ответ:

32

22. Радиус окружности, описанной около квадрата, равен 28√2 . Найдите длину стороны этого квадрата.

Ответ:

56

23. Угол A четырёхугольника ABCD, вписанного в окружность, равен 112° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

68

24. Угол A четырёхугольника ABCD, вписанного в окружность, равен 56° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

124

25. Четырёхугольник ABCD описан около окружности, AB =12, BC = 6, CD =13. Найдите AD.

Ответ:

19

26. Четырёхугольник ABCD описан около окружности, AB =11, BC = 7, CD =12. Найдите AD.

Ответ:

16

27. Угол A четырёхугольника ABCD , вписанного в окружность, равен 37° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:

143