Разложение многочленов на множители
Приветствуем Вас уважаемые школьники и их родители. В этой серии обучающих школьных видео уроков, Вы сможете ознакомиться по предмету Алгебра 7 класс и изучить тему “Разложение многочленов на множители”.

Разложение многочленов на множители
Обучающие уроки преподает учитель школы «Логос ЛВ» Тарасов Валентин Алексеевич. Вы сможете узнать, что как происходит разложение многочленов на множители. Если вы прошли другие темы по предмету Алгебра и не смогли их понять то сможете изучить по следующим ниже приведенным ссылкам.
Разложение многочленов на множители. Вынесение общего множителя за скобки.
На данном уроке мы приступим к изучению большой темы – разложение многочлена на множители – и рассмотрим первый способ разложения: вынесение общего множителя за скобки. Мы сформулируем общее правило и решим несколько простых примеров. После перейдем к более сложным типовым задачам.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Разложение многочленов на множители. Способ группировки.
На данном уроке мы изучим второй метод разложения многочлена на множители – метод группировки, он базируется на ранее изученном методе вынесения общего множителя за скобки. Мы дадим общее рекомендации касательно решения задач и решим несколько примеров, простых и более сложных. Кроме того, решим вычислительные задачи.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Способ группировки в более сложных задачах и уравнениях.
На данном уроке мы решим много различных достаточно сложных задач с применением метода группировки. Мы решим много уравнений и научимся геометрически их моделировать.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Разложение многочленов на множители в комбинации с формулами сокращённого умножения.
На данном уроке мы научимся раскладывать многочлен на множители с применением всех ранее изученных методов. Мы научимся решать задачи с различными комбинациями формул сокращенного умножения и методов разложения.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
На данном уроке мы вспомним все ранее изученные методы разложения многочлена на множители и рассмотрим примеры их применения, кроме того, изучим новый метод – метод выделения полного квадрата и научимся применять его при решении различных задач.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Алгебраические дроби. Сокращение алгебраических дробей.
На данном уроке мы сформируем понятие и дадим определение алгебраической дроби, проведем многочисленные аналогии с арифметической дробью. Решим много примеров различной сложности на сокращение алгебраических дробей.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Алгебраические дроби. Сокращение алгебраических дробей в более сложных случаях.
На данном уроке мы вспомним понятие алгебраической дроби и основы работы с ней. Мы приступим к решению более сложных примеров, в которых не всегда нужно применять очевидные формулы, а иногда стоит задуматься и приступить к разложению совсем с другой стороны.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Тождества.
На данном уроке мы сформируем понятие и дадим определение тождества, сформулируем его отличия от уравнения. Кроме того, мы научимся определять допустимые значения переменных. Мы решим много различных примеров, связанных с тождествами и тождественными преобразованиями.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Многочлены. Обзор.
На этом уроке мы вспомним основные определения, связанные с многочленами, вспомним теоремы о степенях, разберем примеры на приведение одночлена и многочлена к стандартному виду, на разложение многочлена на множители, вспомним формулы сокращенного умножения, разберем пример деления многочленов.
Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru
Мне нравитсяНе нравится
Необходимая теория.
Теорема.
Любой многочлен степени n вида представляется произведением постоянного множителя при старшей степени и n линейных множителей , i=1, 2, …, n, то есть , причем , i=1, 2, …, n являются корнями многочлена.
Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.
К примеру, если корни и многочлена являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде ![]() , где
, где
Замечание.
Среди корней многочлена могут быть повторяющиеся.
Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу.
Основная теорема алгебры.
Всякий многочлен степени n имеет по крайней мере один корень (комплексный или действительный).
Теорема Безу.
При делении многочлена на (x-s) получается остаток, равный значению многочлена в точке s, то есть
![]() , где есть многочлен степени n-1.
, где есть многочлен степени n-1.
Следствие из теоремы Безу.
Если s – корень многочлена , то ![]() .
.
Это следствие будем достаточно часто употреблять при описании решения примеров.
Способ группировки
Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение
ab — 5a + bc — 5c
Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:
ab — 5a + bc — 5c = (ab — 5a) + (bc — 5c) = a(b — 5) + c(b — 5)
Теперь можно вынести выражение b – 5:
a(b — 5) + c(b — 5) = (b — 5)(a + c)
Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.
Пример. Разложим полином 6xy + ab– 2bx– 3ay.
Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:
6xy + ab — 2bx — 3ay = 6xy — 2bx + ab — 3ay = (6xy — 2bx) + (ab — 3ay) = 2x(3y — b) + a(b — 3y)
Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:
(b — 3y) = — (3y — b)
Используем эту замену:
2x(3y — b) + a(b — 3y) = 2x(3y — b) — a(3y — b) = (3y — b)(2x — a)
В результате получили тождество:
6xy + ab — 2bx — 3ay = (3y – b)(2x – a)
Ответ: (3y – b)(2x – a)
Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме
x2 — 3xy + xz + 2x — 6y + 2z
можно сгруппировать первые три и последние 3 одночлена:
x2 — 3xy + xz + 2x — 6y + 2z = (x2 — 3xy + xz) + (2x — 6y + 2z) = x(x — 3y + z) + 2(x — 3y + z) = (x + 2)(x — 3y + z)
Теперь рассмотрим задание повышенной сложности
Пример. Разложите квадратный трехчлен x2– 8x +15.
Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:
-8x = -3x — 5x
Тогда исходный трехчлен можно представить следующим образом:
x2 — 8x + 15 = x2 — 3x — 5x + 15
Сгруппируем слагаемые:
x2 — 3x — 5x + 15 = (x2 — 3x) + (- 5x + 15) = x(x — 3) — 5(x — 3) = (x — 5)(x — 3)
Ответ: (x– 5)(х – 3).
Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:
(x + a)(x + b) = x2 + xa + xb + ab = x2 + (a + b)x + ab
Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x2– 8x +15, надо подобрать подходящие коэффициенты при переменных:
С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда
(x — 3)(x — 5) = x2 * 8x + 15
в чем можно убедиться, раскрыв скобки.
Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:
x2 * 8x + 15 = (2x — 6)(0.5x — 2.5)
Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:
(2x — 6)(0.5x — 2.5) = (x — 3) * 2 * (0.5x — 2.5) = (x — 3)(x — 5)
В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,
x2 — x + 1
невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.
Вынесение минуса за скобки
Еще один случай, на котором следует обратить внимание — это вынесение за скобки минуса. Только мы выносим не сам знак, а минус единицу
Часто это помогает упростить выражение и сделать его проще.
Пример 1. Вынести минус за скобки в выражении: -10 + (-1) + (-3)
Чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые с противоположными знаками:
Найдем решение для каждого выражения:
-(10 + 1 + 3) = -(14) = -14
Поэтому между выражениями можно поставить знак равенства, потому что они равны одному и тому же значению:
-10 + (-1) + (-3) = -(10 + 1 + 3)
Пример 2. Вынести минус за скобки в выражении: -3 + 5 + 11
Ставим минус и рядом в скобках записываем выражение с противоположным знаком у каждого слагаемого:
-3 + 5 + 11 = -(3 — 5 — 11)
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица.
Видео:Раскрытие скобок. 6 класс.Скачать
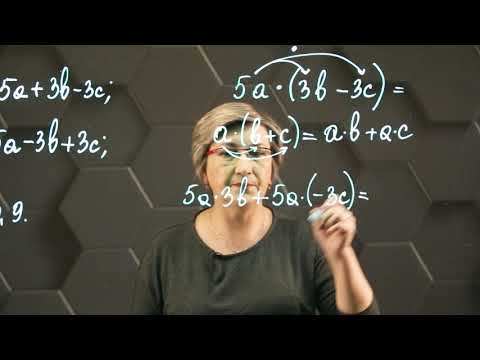
Слайды и текст этой презентации
Слайд 2Что называют разложением многочлена на множители?
a2 – 5ab = a2
5b)
(a – 5) (а + 5)
(a – 6) (а + 6)

Слайд 38 – a3 = x3 + 64 = a3 –
25а =а(а + 4b) a2 + 4ab = (2 –
a)(4 + 2а + a2
(х + 4)(х2 – 4х + 16)
а(а – 5)(а + 5)
Разложите на множители


Слайд 5Решите уравнения(х – 2)(х + 2) = 0 Х= 2

Слайд 6х2 – 16 = 0 (х – 4)(х + 4)
Ответ: — 4; 4
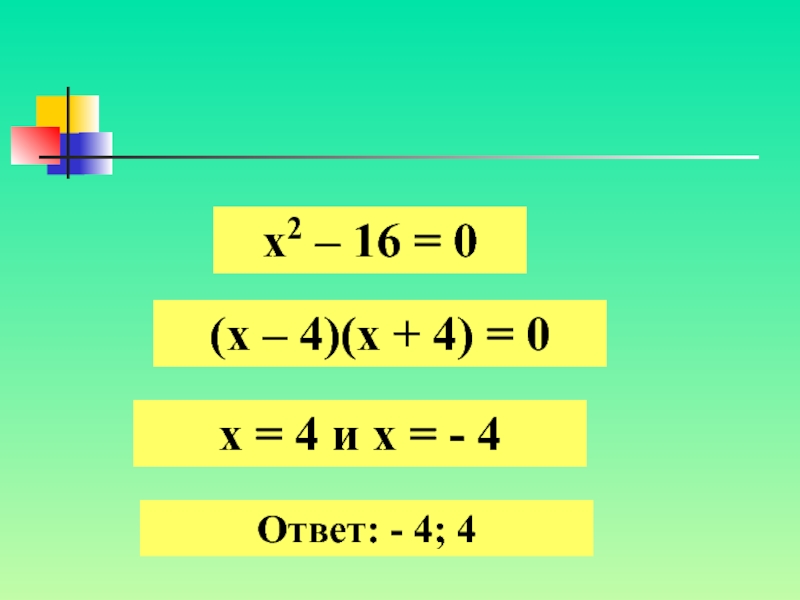
Слайд 7х2 + 10х + 25 =0 (х + 5)2 =
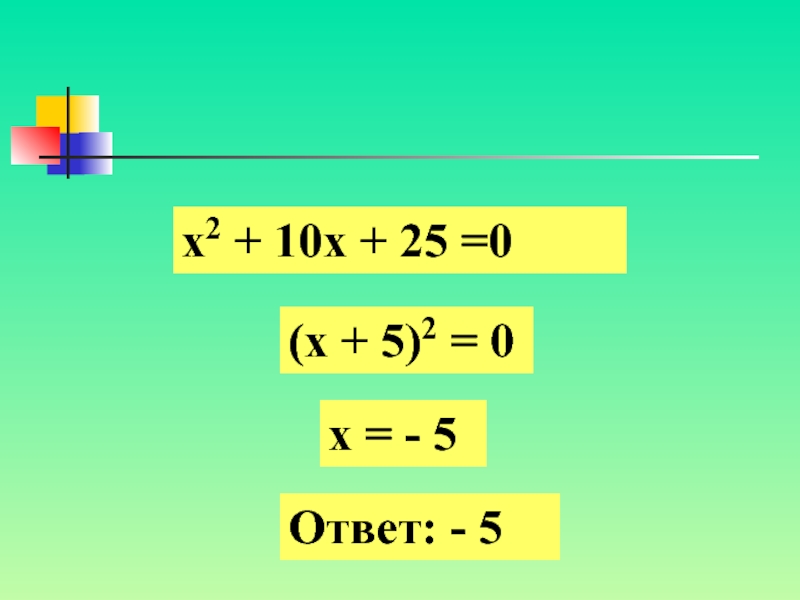
Слайд 89х – х3 = 0 х(9-х2) = 0 х(3
– х)(3 + х) = 0 х = 0
или 3 – х = 0 или 3 + х = 0
х = 0 или х = 3 или х = — 3
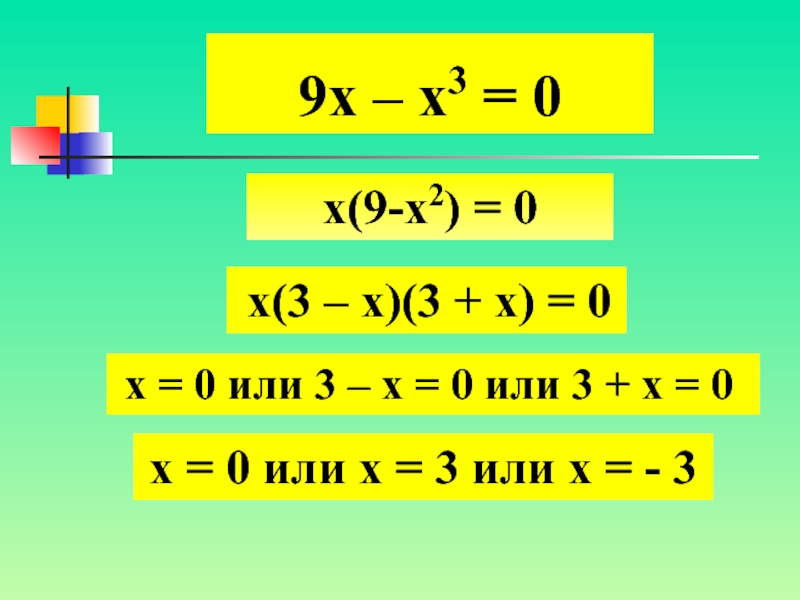
Слайд 9Разложение на множители позволило нам сократить дробь. Найдите значение числового
(53-47)(53+47) (61-39)(61+39)
=
6•10022•100
=
=
6 22
=
3 11

Слайд 10
Алгоритм отыскания общего множителя нескольких одночленов 1. Найти
наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, —
он и будет общим числовым множителем
Вынесение общего множителя за скобки

Слайд 11Найти переменные, которые входят в каждый член многочлена, и выбрать
для каждой из них наименьший
(из имеющихся) показатель степени.
3. Произведение
коэффициента, найденного на первом шаге, является общим множителем, который выносят за скобки.

Слайд 12Разложить на множители:
-x4y3-2x3y2+5×2.Воспользуемся сформулированным алгоритмом.Наибольший общий делитель коэффициентов –1, -2
и 5 равен 1.Переменная x входит во все члены многочлена
с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.

Слайд 13Переменная y входит не во все члены многочлена; значит, ее
нельзя вынести за скобки.Вывод: за скобки можно вынести x2, в
данном случае целесообразнее вынести -x2.
-x4y3-2x3y2+5×2 =
-x2(x2y3+2xy2-5)
Получим:

Слайд 14Способ группировки
Рассмотрим пример:
разложите на множители многочлен х3+х2у– 4у – 4х
= (х2+х2у) – (4х+4у) = = х2 (х + у)
– 4(х + у) =
х + у)(х2 – 4) =
(х + у)(х2 – 4) =
(х + у)(х – 2)(х + 2)

Слайд 15bx2 + 2b2 – b3 – 2×2 = (bx2 –
b3) – (2×2–2b2)= = b(x2 – b2) –2(x2 – b2)
=
(b – 2)(x2 – b2) =
(b – 2)(x – b)(x + b)
Способ группировки

Слайд 16Разложение многочлена на множители с помощью формул сокращенного умножения
Вспомните эти

Слайд 17 Первую из этих формул можно применять к выражению,
вторую и третью – к выражению, представляющему собой разность (или сумму) кубов; Последние две формулы применяются к трехчлену, представляющему собой полный квадрат, т.е. содержащему сумму квадратов двух выражений и удвоенное произведение тех же выражений.
a2-b2=(a-b)(a+b);
a3-b3=(a-b)(a2+ab+b2);a3+b3=(a+b)(a2-ab+b2);
a2+2ab+b2=(a+b)2;a2-2ab+b2=(a-b)2.

Слайд 18 Воспользовались формулой суммы кубов.а6 + 27b3 =(a2)3 + (3b)3
== (a2 + 3b)(a4 – 3a2b + 9b2)

Слайд 19 Х 2 40,8ху + 0,16у 2
Х 2 2=2 · 1 2х · 0,4у +
(0,4у)2
=
Х2
0,4у
2
=
Воспользовались формулой квадрата разности.

= (х3 – 2а2) (х3 + 2а2)

Слайд 21Разложение многочлена
на множители с помощью комбинации различных приемовВ математике не
так часто бывает, чтобы при решении примера применялся только один
прием, чаще встречаются комбинированные примеры, где сначала используется один прием, затем другой и т.д. Чтобы успешно решать такие примеры, мало знать сами приемы, надо еще уметь выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Вот такие комбинированные примеры мы и рассмотрим.

Слайд 22 Сначала займемся вынесением общего множителя за скобки. Рассмотрим
коэффициенты 36, 96, 64. Все они делятся на 4, причем
это – наибольший общий делитель, вынесем его за скобки. Во все члены многочлена входит переменная a (соответственно a6, a4, a2), поэтому за скобки можно вынести a2. Точно так же во все члены многочлена входит переменная b (соответственно b3, b4, b5) – за скобки можно вынести b3.
1. Разложить на множители многочлен
36a6b3-96a4b4+64a2b5

Слайд 23Итак, за скобки вынесем 4a2b3.
Тогда получим:36a6b3-96a4b4+64a2b5 =
4a2b3(9a4-24a2b+16b2)2) Рассмотрим
трехчлен в скобках: 9a4-24a2b+16b2. Выясним, не является ли он полным
квадратом. Имеем:
9a4-24a2b+16b2=(3a2)2+(4b)2-2·3a2·4b.

Слайд 24Все условия полного квадрата соблюдены, следовательно,
9a4-24a2b+16b2=
3) Комбинируя два приема
(вынесение общего множителя за скобки и использование формул сокращенного умножения),
получаем окончательный результат:
(3a2-4b)2.
36a6b3-96a4b4+64a2b5=4a2b3(3a2-4b)2.

Слайд 252. Разложить на множители
x4+x2a2+a4Применим метод выделения полного квадрата. Для
=
= (x2+a2+xa) · (х2 + а2 – ха)

Слайд 263. Разложить на множители
n3+3n2+2nСначала воспользуемся тем, что n можно
вынести за скобки: n(n2+3n+2).Теперь к трехчлену n2+3n+2 применим способ группировки,
предварительно представив 3n в виде 2n+n. Получим:


Выделение квадрата
По сути, выделение общего квадрата соответствует преобразованию, при котором трёхчлен представляют в виде (k + e)2 или (k — e)2. Метод используется для решения биквадратных уравнений. Для выделения полного квадрата при разложении многочлена на множители применяют две формулы:
- k2 + 2 * k * e + e2 = (k + e)2.
- k2 — 2 * k * e + e2 = (k — e)2.
Например, нужно упростить дробь: (k4 + 4 * e4) / (k4 + 2 * e2 + 2 * k * e). Необходимо разложить числитель, используя формулы для полного квадрата: (k4 + 4 * e4) = (k4 + 4 * e2 * k2 + 4 * e 4). Значит, если отнять от многочлена 4 * k2 * e2, то получится уравнение: (k2 + 2 * e2) * 2 − 4 * k2 * e2. Используя формулу умножения квадратов, верно будет записать: (k2 + 2 e 2 − 2 * k * e) * (k2 + 2 e 2 + 2 * k * e).

Заменив полученным выражением числитель, можно будет его часть взаимно сократить со знаменателем. В итоге получится простое выражение: h2 + 2 * e2 − 2 * h * e.
Простое разложение
На уроках математики ученикам предлагают разложить на простые множители числа с помощью столбика (двух колонок). Делается это по следующему алгоритму. Исходное число проверяют на возможность деления без остатка на два. Если делится, то рисуют две колонки, в правую вписывают двойку, а в левую число, получившееся после деления на него исходного. В обратном случае вместо двойки используют цифру три. Далее действия повторяют для числа, находящегося уже в правой колонке. Выполняют деление до тех пор, пока в левой колонке не останется единица. Например, число 1176 можно разложить следующим образом:
1176 | 2 (1176 / 2 = 588).

588 | 2 (588 / 2 = 294).
294 | 2 (294 / 2 = 147).
147 | 2 (147 / 3 = 49).
49 | 2 (49 / 7 = 7).
7 | 2 (7 / 7 = 1).
1176 = 2 * 2 * 2 * 3 * 7 * 7 = 23 * 3 * 72.
Для того чтобы понять алгоритм, лучше рассмотреть ещё несколько интересных примеров:
- 7140 = 2 • 2 • 3 • 5 • 7 • 17 = 2 2 • 3 • 5 • 7 • 17;
- 5544 = 2 • 2 • 2 • 3 • 3 • 7 • 11 = 2 3 • 32 • 7 • 11;
- 4104 = 2 • 2 • 2 • 3 • 3 • 3 • 19 = 2 3 • 33 • 19;
- 546 = 2 • 3 • 7 • 13;
- 510 = 2 • 3 • 5 • 17;
- 495 = 3 • 3 • 5 • 11 = 3 2 • 5 • 11;
- 224 = 2 • 2 • 2 • 2 • 2 • 7 = 2 5 • 7;
- 208 = 2 • 2 • 2 • 2 • 13 = 2 4 • 13;
- 156 = 2 • 2 • 3 • 13 = 2 2 • 3 • 13;
- 126 = 2 • 3 • 3 • 7 = 2 • 3 2 • 7;
- 118 = 2 • 59.
Применение формул сокращенного умножения
Формулы сокращенного умножения часто значительно облегчают разложение на множители, позволяя избежать разложения одночленов на подобные слагаемые и обойтись без вставки новых одночленов .
Пример:
Разложить на множители
Решение:
Мы видим, что исследуемый многочлен есть разность квадратов чисел х и 2. Следовательно, его можно записать в виде произведения суммы этих чисел на их разность
Пример:
Разложить на множители
Решение:
Мы видим, что сумма первых трех слагаемых есть квадрат суммы чисел х и 2у. Действительно, квадрат первого числа равен , удвоенное произведение первого на второе равно 4ху, квадрат второго равен Итак,
![]()
Теперь наш многочлен приведен к виду разности квадратов чисел (х + 2у) и 3z. Следовательно, его можно представить в виде произведения суммы этих чисел на их разность
![]()
Пример:
Разложить на множители многочлен
Решение:
Прежде всего надо вынести за скобку 2х
Теперь мы видим, что многочлен, находящийся в скобке, есть разность кубов чисел х и 2у. По сокращенной формуле мы знаем, что разность кубов двух чисел равна произведению разности этих чисел на «неполный квадрат их суммы». Итак,
![]()
Окончательно получаем
![]()
Мы прерывали запись действий рассуждениями. Конечно, при решении такого рода примеров рассуждения надлежит производить без записи—вслух или про себя, и запись должна выглядеть так:
![]()
Более сложные примеры с решением
Мы разобрали несколько приемов разложения многочлена на множители— вынесение за скобку, способ группировки, разложение одночленов на подобные слагаемые, использование формул сокращенного умножения. Не существует никаких общих правил для того, какими из этих приемов и в каких сочетаниях их друг с другом надлежит пользоваться для достижения цели в каждом частном случае. (Конечно, если это возможно, следует раньше всего сделать вынесение за скобку. Это никогда не ведет к усложнению, но часто упрощает задачу.) Поэтому, прежде чем приступить к выкладке, необходимо вдуматься в строение разлагаемого многочлена и составить план действий. Для того чтобы показать, как составлять этот план, рассмотрим несколько более сложных примеров.
Пример:
Разложить на множители многочлен
![]()
Решение:
Мы видим, что если из суммы первых двух слагаемых вынести х у, в скобке останется х + у. Попробуем сгруппировать остальные слагаемые так, чтобы х + у входило множителем в сумму слагаемых каждой группы. Мы видим, что «хорошей» в этом смысле группой является сумма при вынесении из нее за скобку в скобке останется х + у. Остается группа слагаемых Если в этой группе вынести за скобку z, то в скобке oстанется т. е. квадрат суммы (х + у). Итак,
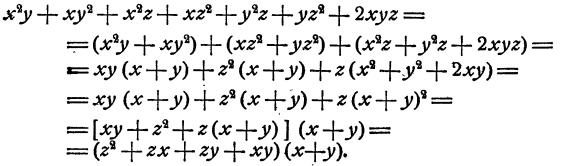
Первый множитель можно разложить дальше, воспользовавшись способом группировки:
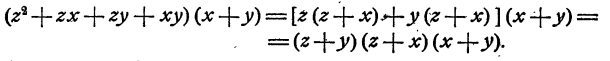
Пример:
Решение:
Здесь прежде всего бросается в глаза, сходство с кубом суммы или разности чисел , х и 1. Однако это сходство обманчиво— знаки не те! Поэтому следует искать другой прием. Например, хорошо сгруппировать вместе крайние члены и 1 и средние — , ибо содержит , множитель x + l по формуле суммы кубов, и тот же множитель х + 1 обнаруживается в ; посредством вынесения за скобку. Итак,
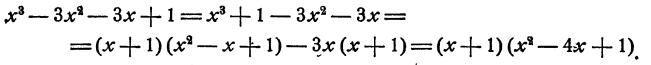
Пример:
Решение:
Здесь целесообразно член разбить на сумму двух членов и Действительно, тогда сумма первых трех членов, а также взятая с обратным знаком сумма последних трех представится в виде квадратов, и после этого останется применить формулу для разложения разности квадратов. Осуществим этот план:
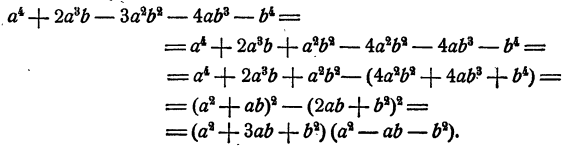
Пример:
Решение:
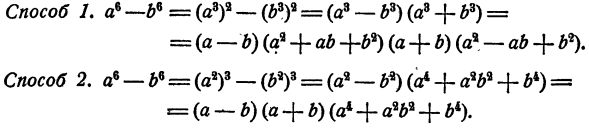
Сравнивая результаты, мы видим, что разлагается на два множителя:. В этом можно убедиться и непосредственно:
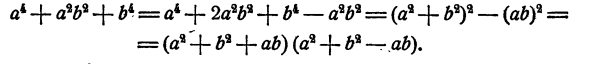
Пример:
Разложить на множители
Решение:
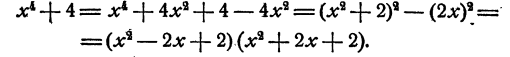
Пример:
Разложить на множители
Решение:
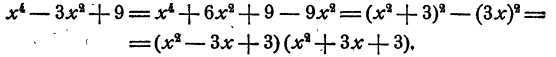
В последних двух примерах разложение удается посредством преобразования в разность квадратов. Этот прием часто ведет к цели при разложении так называемого биквадратного трехчлена, т. е. трехчлена, составленного из четвертой и второй степеней Одной буквы с некоторыми коэффициентами и свободного члена.
Использование онлайн-калькуляторов

Порой, для решения сложных заданий нужно затратить много времени. При этом всегда существует риск допустить ошибку при расчётах. Чтобы этого избежать или проверить свой ответ, можно воспользоваться сайтами, предлагающие онлайн-калькуляторы. Использовать их сможет даже пользователь, совершенно не понимающий методов, используемых для упрощения выражений.
Расчёт обычно занимает менее 30 секунд. Приложений для упрощений уравнений достаточно много. Написаны они на Паскале или javascript. Появление ошибки при вычислении невозможно. Нередко на этих сайтах ещё и содержится информация о способах упрощения полиномов.
Для того чтобы получить ответ, необходимо будет с помощью браузера зайти на сайт онлайн-калькулятора и заполнить предлагаемые им поля. После того как упрощаемое выражение будет вписано, следует нажать кнопку «Рассчитать» или «Упростить выражение» и получить ответ с пошаговым решением.
Применение вынесения за скобку к расположению многочлена по степеням одной буквы
Многочлены, содержащие одну букву, целесообразно записывать в порядке убывания степеней. Это оказалось полезным при умножении многочленов, это полезно при разложении на множители и при делении многочлена на многочлен.
Такая запись часто оказывается удобной и для многочленов, содержащих несколько букв. При этом из всех букв нужно выбрать одну, главную букву и записывать, одночлены в порядке убывания степеней этой буквы.
Например, многочлен расположен в порядке убывания степеней буквы х. Если бы мы в этом многочлене в качестве главной буквы взяли вместо х другую букву, например b, мы должны были бы записать его члены в другом порядке, именно
При таком расположении часто оказывается, что имеется несколько, членов, содержащих главную букву в одной и той же степени. В нашем примере имеется два члена, содержащих х в первой степени. Для того чтобы еще более подчеркнуть, что за главную букву принимается х, целесообразно рассматривать члены, содержащие х в одной и той же степени, как подобные, и соединять их вместе посредством вынесения буквы х в надлежащей степени за скобку из алгебраической суммы таких членов. Так,
![]()
В такой записи многочлен выглядит как многочлен, зависящий только от одной буквы х, но с буквенными коэффициентами и с буквенным свободным членом. Так, коэффициентами в многочлене являются и свободным членом является abc.
Естественно поставить вопрос о том, какую букву нужно выбрать за главную, если мы хотим расположить по степеням одной буквы многочлен, зависящий от нескольких букв.
Если многочлен рассматривается без связи с какой-либо задачей, то выбор главной буквы совершенно безразличен. Если же многочлен получается при решении задачи, часто условие задачи подсказывает, какую букву следует считать главной.
Рассмотрим один пример этого рода.
Задача:
Коробка имеет длину а см, ширину b см. Требуется найти высоту, при которой площадь поверхности коробки равняется s см.
Решение:
Обозначим высоту буквой х. Поверхность коробки составлена из шести прямоугольников. Два из этих прямоугольников (дно и крышка) имеют площадь аb другие два (левая и правая стенки) имеют площадь bх , и последние два (передняя и задняя стенки) имеют площадь ах . Следовательно, между четырьмя буквами a, b, s и х имеется следующая зависимость:
или, что то- же самое,
Мы получили уравнение, в левой части которого находится многочлен, зависящий от букв a, b, x и s Какую же из этих .четырех букв следует принять за главную букву? Конечно, х, так как х играет особую роль в задаче. Числа а, b и s — это числа известные данные. Число х — неизвестное. Поэтому полученное нами уравнение следует записать так:
А теперь его легко решить.
Сумма чисел равна нулю. Следовательно, это противоположные числа:
![]()
Произведение числа х на число 2а + 2b равно s — 2аb. Следовательно,
Задача решена.
Неприводимые множители
Решая различные задачи, можно столкнуться со сложными выражениями, которые, как кажется, разложить нельзя. Например, (2 * p2 — 5 * p — 3)/(3 * p — 9). В числителе дроби находится квадратный трёхчлен, который на самом деле можно разложить. Для того чтобы его можно было упростить, используется формула: ar2 + br + p = a (r — r1) * (r — r2), где r1 и r2 корни выражения.
Чтобы найти решения для линейного уравнения, необходимо определить дискриминант. То есть нужно из задачи отделить числитель, найти его решения и подставить найденные значения в формулу разложения.
Для рассматриваемого примера дискриминант квадратного уравнения будет равняться: Д = 25 — 4*2 (-3) = 49. Отсюда p1 = (5 + 7)/4 = 3, p2 = (5 — 7)/4 = -½. Подставив полученные корни в формулу, можно запись: 2 * (p — 3) * (p + ½).
Теперь вместо числителя нужно подставить полученное разложение: (2*p2 — 5*p — 3)/(3*p — 9) = 2*(p — 3) * (p + ½)/3 * (p — 3) = (2 *p + 1)/3.
Термины и понятия
Под разложением в математике понимается операция, которую выполняют для превращения сложного неудобного для вычисления примера в простой. В учебниках и литературе такое преобразование выражений называется тождественным, то есть без изменения сути задания.
Из слова «множители» можно понять, что в превращении используется умножение. Зная, как разложить полином на простые числа, можно быстро решать задачи на действия с корнями и сложными дробями. Например, выражение (3*h*y + 9*y — 8*h — 24) * (3*h — ![]() после упрощения примет вид: h + 3 — и быстро решается в уме.
после упрощения примет вид: h + 3 — и быстро решается в уме.
В математике все алгебраические выражения могут быть:

- Одночленными. Это уравнения, состоящие из чисел, натуральных степеней и не содержащие никаких других арифметических действий, кроме умножения. Числовой множитель выражения называют коэффициентом.
- Многочленными. Включающими в себя сумму нескольких одночленов. Если выражение, кроме произведения, не содержит другие арифметические операции, такие как деление, возведение в степень, его называют целым.
Каноническим правилом является следующее: любое простое число можно представить как произведение его составляющих. Так, 12 можно представить как 6 х 2, в свою очередь, 6 — как 3 х 2. Таким образом, будет верной запись: 12 = 3 х 2 х 2. На этом принципе построено упрощение любого выражения. Простые цифры 3, 2, 2 и являются множителями, на которые раскладывают пример.
Существуют пять способов преобразования многочленов (полиномов):
- вынесение общего коэффициента для каждого члена за скобку;
- трансформация по формулам сокращённого умножения;
- способ группирования;
- нахождение и выделения полного квадрата;
- разложение на простые множители.
Формулы умножения
Довольно часто для упрощения расчётов используют формулы сокращённого умножения. Всего существует семь выражений, которые необходимо выучить. Найти их можно в таблицах любого учебника по алгебре за седьмой класс. Смысл этих теорем в следующем:

- Разность двух членов, стоящих во второй степени, прямо пропорциональна произведению разности этих членов на их сумму. Например, 16 2 — 3 2 = (16 — 3) * (16 + 3) = 247 или 9 * h 2 — 4 * e 2 * h 2 = (3 * h — 2 * e * h) * (3 * h — 2 * e * h).
- Квадрат суммы двух членов можно разложить на квадрат первого элемента и удвоенное произведение его на второй элемент, прибавив квадрат второго члена. Используя это правило, можно быстро находить квадрат числа без использования калькулятора. Например, 114 2 = (100 +14) = 100 2 + 2 * 100 * 14 + 14 2 = 10000 + 2800 + 196 = 12966.
- Квадрат разности двух членов равняется квадрату первого члена с вычетом из него двойного произведения первого на второй с добавлением квадрата второго члена. В этом правиле используют обыкновенное раскрытие скобок. Например, (6 — 3) 2 = 6 2 — 2 * 6 * 3 + 3 2 = (3 — 6) 2 = 9 .
- Кубическая сумма двух выражений определяется кубом первого члена с прибавлением к нему утроенного произведения исходного числа в степени два на второй член, плюс увеличенное в три раза произведение исходного числа на квадрат второго с прибавлением этого элемента в третьей степени. Например, (2h+7e) 3 = (2 * h) 3 + 3 * 2 * h 2 * 7* e + 3 * 2h * (7 * e) 2 + (7 * e) 3.
- Куб разности находится вычитанием из исходного числа утроенного произведения первого члена, возведённого во вторую степень, с прибавлением утроенного произведения исходного члена на второй в степени два минус его куб. Например, (4 * h − 2 * e) 3 = (4 * h) 3 − 3 * (4 * h) 2 * 2 * e + 3 * 4 * h * (2 * e) 2 − (2 * e) 3 .
- Сумма кубов находится как произведение суммы членов на неполный квадрат разности: (5 * h) 3 + 8 3 = (5 * h +
 * ((5 * h) 2 − 5 * h * 8 + 8 2). Неполным квадратом называют выражение: (h 2 — h * e + e 2).
* ((5 * h) 2 − 5 * h * 8 + 8 2). Неполным квадратом называют выражение: (h 2 — h * e + e 2). - Разность кубов равна выражению, полученному перемножением разности двух чисел на неполный квадрат суммы: h3− e3 = (h − e) * ((h 2 +h) * (e + e 2)).
Все эти формулы умножения можно использовать также в обратную сторону, то есть собирать многочлен. Например, для решения примеров типа: «квадратный трёхчлен разложен на множители, найдите а». Если понять смысл этих формул, то запомнить их наизусть будет довольно легко.






























