Основные сведения о рациональных выражениях в алгебре

Среднее гармоническое

Турист проплыл по течению реки до остановки со скоростью $\textcolor{blue}{v_1} \space км/ч,$ затем он отправился обратно, но плыл уже против течения реки со скоростью $\textcolor{darkgreen}{v_2} \space км/ч.$ Найдите среднюю скорость туриста на всем пути движения.

Пусть расстояние до остановки равно $\textcolor{orange}{s} \space км,$ тогда все расстояние, которое проплыл турист, будет равно $2\textcolor{orange}{s},$ а время движения туриста вперед и назад равно соответственно: $\frac{\textcolor{orange}{s}}{\textcolor{blue}{v_1}}\space ч$ и $\frac{\textcolor{orange}{s}}{\textcolor{darkgreen}{v_2}}\space ч.$

Чтобы найти среднюю скорость, мы должны все расстояние разделить на все время:$$v_{ср}=\frac{2s}{\frac{s}{v_1}+\frac{s}{v_2}}$$

Сократив дробь на $s,$ мы получим формулу для средней скорости при участках пути одинаковой длины:$$v_{ср}=\frac{2}{\frac{1}{v_1}+\frac{1}{v_2}}$$

Показать решение

Скрыть

$$\frac{2\textcolor{orange}{s}}{\frac{\textcolor{orange}{s}}{v_1}+\frac{\textcolor{orange}{s}}{v_2}}=\frac{2\cdot \textcolor{orange}{s}}{\frac{1}{v_1}\cdot \textcolor{orange}{s}+\frac{1}{v_2}\cdot \textcolor{orange}{s}}=$$ $$=\frac{2\cdot \cancel{\textcolor{orange}{s}}}{\cancel{\textcolor{orange}{s}}\cdot (\frac{1}{v_1}+\frac{1}{v_2})}=\frac{2}{\frac{1}{v_1}+\frac{1}{v_2}}$$

расчет средней скорости

Средняя скорость на равных участках пути вычисляется не по формуле среднего арифметического чисел, а по формуле среднего гармонического ряда положительных чисел.

{"questions":[{"content":"Лыжник прошел дистанцию $\\textcolor{purple}{три}$ раза. Первый раз со скоростью $\\textcolor{darkgreen}{10} \\space км/ч,$ второй раз со — скоростью $\\textcolor{blue}{12} \\space км/ч,$ а затем — со скоростью $\\textcolor{coral}{6} \\space км/ч.$ Найдите среднюю скорость лыжника на всем пути.`image-1``fill_choice_big-27`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/07/na-lyzhah-lyzhi-1-2.svg","width":"400"},"fill_choice_big-27":{"type":"fill_choice_big","options":,"placeholder":0,"answer":0}},"step":1,"hints":}]}

Иррациональные выражения, выражения с корнями

Знакомство с понятием корня приводит к возникновению выражений, в записях которых присутствуют знаки корней (радикалы). Такие выражения обычно называют выражениями с корнями или выражениями, содержащими операцию извлечения корня. Их же называют иррациональными выражениями.

Определение.

Иррациональные выражения (выражения с корнями) — это выражения, которые содержат в записи знаки корней.

На основании данного определения , a+1/(a1/2+2), и — это все иррациональные выражения, так как в каждом из них присутствует хотя бы один знак корня.

Так как корни тесно связаны со степенями, то они очень часто присутствуют в выражениях совместно. Например, и т.п.

В статье преобразование иррациональных выражений (выражений с корнями) мы поговорим про основные приемы работы с иррациональными выражениями.

Алгебра 7-9 классы. 13. Дробные рациональные выражения. Действия с рациональными дробями

Подробности

Категория: Алгебра 7-9 классы

1. Рациональные выражения

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.Целые и дробные выражения называют рациональными выражениями.Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смыслапри а = 0. При всех остальных значениях а это выражение имеет

смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.Выражение вида называется, как известно, дробью.Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.Примерами рациональных дробей служат дроби

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Пример 1. Найдем допустимые значения переменной в дроби

Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а — 9) = 0.Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.

Пример 2. При каком значении х значение дроби равно нулю ?

 Дробь  равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.

Числители дроби равен нулю, если , т.е.

или . Итак, числитель дроби равен нулю при x = 7 и  x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит,  данная дробь равна нулю при x = 7.

2. Основное свойство дроби. Сокращение дробей

Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство

 Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.

Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :

На основании сочетательного и переместительного свойств умножения имеем:

Так как bс ≠ 0, то по определению частного

Значит,

Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство

Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.Равенство (1) выражает основное свойство рациональной дроби:

если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Например,

Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.

Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.

Пример 1. Приведем дробь к знаменателю

Так как то, умножив числитель и знаменатель дроби на , получим:

Множитель называют дополнительным множителем к числителю и знаменателю дроби

Пример 2. Приведем дробь  к знаменателю

Для этого числитель и знаменатель данной дроби умножим на -1:

Дробь можно заменить тождественно равным выражением , поставив знак «минус» перед дробью и заменив  знак в числителе:

Вообще

если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Пример 3. Сократим  дробь

Разложим числитель и знаменатель дроби на множители:

Сократим полученную дробь на общий множитель a + 3:

Итак,

Пример 4. Построим график функции

Область определения функции -множество всех чисел, кроме числа 4. Сократим дробь

Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)

Основные виды преобразований рациональных выражений

Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.

Пример 1

Преобразовать рациональное выражение 3 · x x · y — 1 — 2 · x x · y — 1 .

Решение

Видно, что такое рациональное выражение – это разность 3 · x x · y — 1 и 2 · x x · y — 1 . Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид

3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 · 3 — 2 = x x · y — 1

Ответ:
3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 .

Пример 2

Выполнить преобразование 2 · x · y 4 · (- 4) · x 2: (3 · x — x) .

Решение

Первоначально выполняем действия в скобках 3 · x − x = 2 · x . Данное выражение представляем в виде 2 · x · y 4 · (- 4) · x 2: (3 · x — x) = 2 · x · y 4 · (- 4) · x 2: 2 · x . Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.

Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2 · x · y 4 · (- 4) · x 2: 2 · x = 2 · x · y 4 · (- 4) · x 2: 2: x .

Группируем числовые множители с переменной x , после этого можно выполнять действия со степенями. Получаем, что

2 · x · y 4 · (- 4) · x 2: 2: x = (2 · (- 4) : 2) · (x · x 2: x) · y 4 = — 4 · x 2 · y 4

Ответ:
2 · x · y 4 · (- 4) · x 2: (3 · x — x) = — 4 · x 2 · y 4 .

Пример 3

Преобразовать выражение вида x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 .

Решение

Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида (x · (x + 3) — (3 · x + 1)) : 1 2 · x · 4 + 2 , причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 = x 2 + 3 · x — 3 · x — 1 1 2 · 4 · x + 2 = x 2 — 1 2 · x + 2 .

Преобразуем в числителе формулу разности квадратов, тогда получаем, что

x 2 — 1 2 · x + 2 = (x — 1) · (x + 1) 2 · (x + 1) = x — 1 2

Ответ
: x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 = x — 1 2 .

Задача № 4

\

Давайте выпишем первую дробь и попытаемся разобраться с ней отдельно:

\

\

Переходим ко второй. Сразу посчитаем дискриминант знаменателя:

Он на множители не раскладывается, поэтому запишем следующее:

\

\

Числитель выпишем отдельно:

\

Следовательно, этот многочлен на множители не раскладывается.

Максимум, что мы могли сделать и разложить, мы уже сделали.

Итого переписываем нашу исходную конструкцию и получаем:

\

Все, задача решена.

Если честно, это была не такая уж и сложная задача: там все легко раскладывалось на множители, быстро приводились подобные слагаемые, и все красиво сокращалось. Поэтому сейчас давайте попробуем решить задачку посерьезней.

Представление в виде рациональной дроби

Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.

Пример 4

Представить в виде рациональной дроби a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a .

Решение

Данное выражение можно представить в виде a 2 — 25 a + 3 · 1 a 2 + 5 · a . Умножение выполняется в первую очередь по правилам.

Следует начать с умножения, тогда получим, что

a 2 — 25 a + 3 · 1 a 2 + 5 · a = a — 5 · (a + 5) a + 3 · 1 a · (a + 5) = a — 5 · (a + 5) · 1 (a + 3) · a · (a + 5) = a — 5 (a + 3) · a

Производим представление полученного результата с исходное. Получим, что

a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a — 3 — a — 5 a + 3 · a

Теперь выполняем вычитание:

a + 5 a · a — 3 — a — 5 a + 3 · a = a + 5 · a + 3 a · (a — 3) · (a + 3) — (a — 5) · (a — 3) (a + 3) · a · (a — 3) = = a + 5 · a + 3 — (a — 5) · (a — 3) a · (a — 3) · (a + 3) = a 2 + 3 · a + 5 · a + 15 — (a 2 — 3 · a — 5 · a + 15) a · (a — 3) · (a + 3) = = 16 · a a · (a — 3) · (a + 3) = 16 a — 3 · (a + 3) = 16 a 2 — 9

После чего очевидно, что исходное выражение примет вид 16 a 2 — 9 .

Ответ:
a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 — 9 .

Пример 5

Представить x x + 1 + 1 2 · x — 1 1 + x в виде рациональной дроби.

Решение

Заданное выражение записывается как дробь, в числителе которой имеется x x + 1 + 1 , а в знаменателе 2 · x — 1 1 + x . Необходимо произвести преобразования x x + 1 + 1 . Для этого нужно выполнить сложение дроби и числа. Получаем, что x x + 1 + 1 = x x + 1 + 1 1 = x x + 1 + 1 · (x + 1) 1 · (x + 1) = x x + 1 + x + 1 x + 1 = x + x + 1 x + 1 = 2 · x + 1 x + 1

Следует, что x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 x + 1 2 · x — 1 1 + x

Получившаяся дробь может быть записана как 2 · x + 1 x + 1: 2 · x — 1 1 + x .

После деления придем к рациональной дроби вида

2 · x + 1 x + 1: 2 · x — 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x — 1 = 2 · x + 1 · (1 + x) (x + 1) · (2 · x — 1) = 2 · x + 1 2 · x — 1

Можно решить это иначе.

Вместо деления на 2 · x — 1 1 + x производим умножение на обратную ей 1 + x 2 · x — 1 . Применим распределительное свойство и получаем, что

x x + 1 + 1 2 · x — 1 1 + x = x x + 1 + 1: 2 · x — 1 1 + x = x x + 1 + 1 · 1 + x 2 · x — 1 = = x x + 1 · 1 + x 2 · x — 1 + 1 · 1 + x 2 · x — 1 = x · 1 + x (x + 1) · 2 · x — 1 + 1 + x 2 · x — 1 = = x 2 · x — 1 + 1 + x 2 · x — 1 = x + 1 + x 2 · x — 1 = 2 · x + 1 2 · x — 1

Ответ:
x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 2 · x — 1 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

На данном уроке будут рассмотрены основные сведения о рациональных выражениях и их преобразованиях, а также примеры преобразования рациональных выражений. Данная тема как бы обобщает изученные нами до этого темы. Преобразования рациональных выражений подразумевают сложение, вычитание, умножение, деление, возведение в степень алгебраических дробей, сокращение, разложение на множители и т. п. В рамках урока мы рассмотрим, что такое рациональное выражение, а также разберём примеры на их преобразование.

Тема:
Алгебраические дроби. Арифметические операции над алгебраическими дробями

Урок:
Основные сведения о рациональных выражениях и их преобразованиях

Представление в виде рациональной дроби

Наиболее часто конечной целью преобразования выражений является упрощение их вида. В этом свете самым простым видом, к которому можно преобразовать дробно рациональное выражение, является рациональная (алгебраическая) дробь, и в частном случае многочлен, одночлен или число.

А любое ли рациональное выражение возможно представить в виде рациональной дроби? Ответ утвердительный. Поясним, почему это так.

Как мы уже сказали, всякое рациональное выражение можно рассматривать как многочлены и рациональные дроби, соединенные знаками плюс, минус, умножить и разделить. Все соответствующие действия с многочленами дают многочлен или рациональную дробь. В свою очередь любой многочлен можно преобразовать в алгебраическую дробь, записав его со знаменателем 1. А сложение, вычитание, умножение и деление рациональных дробей в результате дают новую рациональную дробь. Следовательно, выполнив все действия с многочленами и рациональными дробями в рациональном выражении, мы получим рациональную дробь.

Пример.

Представьте в виде рациональной дроби выражение .

Решение.

Исходное рациональное выражение представляет собой разность дроби и произведения дробей вида . Согласно порядку выполнения действий мы сначала должны выполнить умножение, а уже потом – сложение.

Начинаем с умножения алгебраических дробей: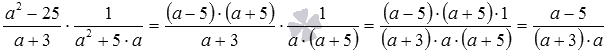

Подставляем полученный результат в исходное рациональное выражение: .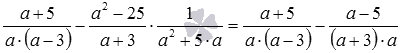

Мы пришли к вычитанию алгебраических дробей с разными знаменателями: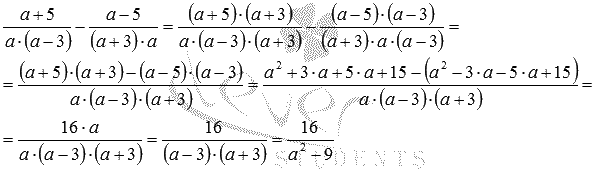

Итак, выполнив действия с рациональными дробями, составляющими исходное рациональное выражение, мы его представили в виде рациональной дроби .

Ответ:

.

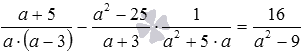Для закрепления материала разберем решение еще одного примера.

Пример.

Представьте рациональное выражение в виде рациональной дроби.

Решение.

Исходное выражение представляет собой дробь, в числителе которой находится сумма , а в знаменателе – дробь . Преобразуем сумму , выполнив : .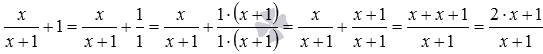

Таким образом, .

Полученную дробь можно переписать в виде частного . Выполнив деление алгебраических дробей, мы придем к нужной нам рациональной дроби: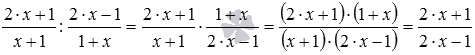

Представление исходного рационального выражения в виде рациональной дроби можно было получить и иначе. Покажем другой способ решения.

Деление на дробь можно было заменить умножением на обратную ей дробь , после чего воспользоваться распределительным свойством умножения относительно сложения. Цепочка преобразований рационального выражения в этом случае выглядела бы так: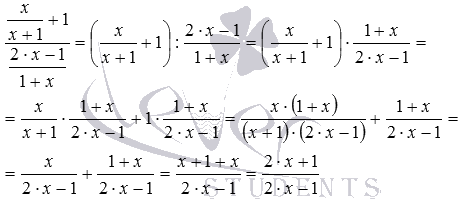

Ответ:

.

Список литературы.

• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
• Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
• Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Понятие рационального выражения

В и классе мы уже изучали дроби и действия над ними. В классе рассматривались рациональные числа, которые, по сути, и являются дробями. Однако до этого мы изучали только так называемые числовые дроби, у которых в числителе и знаменателе стоят какие-то числа либо выражения с числами, но не переменные величины.

Следующие дроби являются числовыми:

Однако нередко в алгебре приходится иметь дело и с дробями, которые содержат переменные. В качестве примера подобных выражений можно привести:

Так как деление на ноль является недопустимой операцией в алгебре, то некоторые дроби могут не иметь смысла. Так, дробь

бессмысленна, так как ее знаменатель 21 – 3•7 равен нулю.

Если дробь содержит переменные величины, то ее значение зависит от этих переменных. Так, дробь

при у = 4 принимает значение, равное 9. Если же у = 3, то эта дробь окажется бессмысленной.

Значения переменных величин, при которых дробь сохраняет свой смысл, называют допустимыми значениями переменных.

Пример. Укажите множество допустимых значений величин х и у для дроби

Решение. Недопустим только случай, при котором в знаменателе находится ноль, то есть когда выполняется равенство

х – у = 0

или равносильное ему равенство

х = у

Следовательно, допустимыми значениями являются все такие пары (х; у), что х ≠ у.

Пример. Каковы допустимые значения величин а и b в дроби

Решение. В данной записи есть три дробных черты, а значит, и три знаменателя:

Ни один из знаменателей не должен равняться нулю, поэтому

Перенесем в последнем неравенстве 2-ое слагаемое вправо, изменив знак (правила преобразований выражений со знаком ≠ точно такие же, как и у равенств):

По свойству пропорции имеем:

1•а ≠ 1•b

а ≠b

Итак, допустимыми являются все значения a и b, при которых а ≠ 0, b≠ 0, a≠b.

Пример. Найдите множество допустимых значений х для дроби

Решение.

Ясно, что знаменатель должен отличаться от нуля:

х2 – 25 ≠ 0

Чтобы найти, при каких значениях неизвестной величины знаменатель обращается в ноль, надо решить уравнение

х2 – 25 = 0

Представим полином в левой части как произведение, применив формулу квадрата разности:

х2 – 52= 0

(х – 5)(х + 5) = 0

х = 5 или х = – 5

Получаем, что исходная дробь сохраняет смысл при любых х, отличных от – 5 и 5.

Порою дроби, содержащие переменные, могут встречаться в тождествах.

Пример. Докажите тождество

Решение. У дроби в левой части знаменатель всегда положителен, поэтому все допустимыми являются все значения c. Согласно свойству операции деления, делимое равно произведению делителя и частного, поэтому для доказательства тождества надо лишь показать справедливость равенства

(с3 – 2с2 + с – 2) = (с – 2)(с2 + 1)

Раскроем скобки в правой части:

(с – 2)(с2 + 1) = с3 – 2с2 + с – 2

Получили одинаковое выражение и для левой, и для правой части тождества, следовательно, оно верное.

Теперь сформулируем понятие рационального выражения.

Среди рациональных выражений выделяют целые и дробные выражения.

Приведем примеры целых рациональных выражений:

А вот несколько примеров дробных рациональных выражений:

Стоит заметить, что дробь и дробное выражение – это два разных понятия. Для иллюстрации приведем два примера:

•  – это дробь, но целое, а не дробное выражение;
• (х + 7):t – это дробное выражение, но не дробь.

Отдельно отметим, что дробь равна нулю тогда, когда ее числитель равен нулю, а знаменатель нет. Если же и знаменатель равен нулю, то получается недопустимое действие – деление на ноль, поэтому дробь не будет иметь смысла.

Пример. Найдите все корни уравнения

Решение. На первый взгляд уравнение кажется сложным, особенно из-за знаменателя. Однако он здесь почти не играет роли. В левой части находится дробь, значит, нулю равен ее знаменатель:

(х – 1)(х + 2) = 0

х – 1 = 0 или х + 2 = 0

х = 1 или х = – 2

Получили два корня. Осталось убедиться, что при этих значениях х дробь не становится бессмысленной, то есть ее знаменатель не обращается в ноль. При х = 1 имеем знаменатель

2•14 – 3•13 + 5•1 – 4 = 2 – 3 + 5 – 4 = 0

поэтому число 1 НЕ является корнем уравнения. Теперь проверим знаменатель при х = – 2:

2•(– 2)4 – 3•( – 2)3 + 5•( – 2) – 4 =

= 32 + 24 – 10 – 4 = 42

Получается, что единственное корень уравнения – это ( – 2).

Ответ: – 2

Порядок действий в рациональных выражениях

Рассмотрим выражение:

$$\Big(\frac{2x-5y}{x+y}-\frac{x}{x+y} \Big):(x-5y)$$

В данном выражении можно найти разность дробей, а затем выполнить деление. В результате мы получим рациональную дробь.

Показать решение

Скрыть

Найдем разность дробей в скобках:$$\frac{2x-5y}{x+y}-\frac{x}{x+y}=\frac{\textcolor{darkgreen}{2x}-5y\textcolor{darkgreen}{-x}}{x+y}=\frac{\textcolor{darkgreen}{x}-5y}{x+y}$$

Выполним деление:$$\frac{x-5y}{x+y}:(x-5y)=\frac{\cancel{\textcolor{orange}{x-5y}}}{x+y} \cdot \frac{1}{\cancel{\textcolor{orange}{x-5y}}}=\frac{1}{x+y}$$

Порядок действий

В рациональных выражениях, так же как и в числовых выражениях, соблюдается порядок действий:

• Сначала считаются степени.
• Затем выполняются действия в скобках.
• Далее выполняется умножение и деление.
• В конце производится сложение и вычитание.

Пример 1

Представим в виде дроби выражение:$$2+y\overset{\textcolor{coral}{2}}-\frac{y+5}{x^2} \overset{\textcolor{blue}{1}}\cdot \frac{13}{2y+10}$$

$\textcolor{blue}{1)}$ Сначала выполняем умножение:$$\frac{y+5}{x^2} \cdot \frac{13}{2y+10}=\textcolor{darkgreen}{\frac{13}{2x^2}}$$

Показать решение

Скрыть

В знаменателе второй дроби вынесем общий множитель $\textcolor{orange}{2}$ за скобки:$$\frac{y+5}{x^2} \cdot \frac{13}{\textcolor{orange}{2}y+\textcolor{orange}{2}\cdot 5}=\frac{y+5}{x^2} \cdot \frac{13}{\textcolor{orange}{2}(y+5)}$$

Сократим и перемножим дроби:$$\frac{\cancel{\textcolor{purple}{y+5}}}{x^2} \cdot \frac{13}{2(\cancel{\textcolor{purple}{y+5}})}=\frac{1 \cdot 13}{x^2 \cdot 2}=\frac{13}{2x^2}$$

$\textcolor{coral}{2)}$ Теперь можно выполнить вычитание:$$2+y-\textcolor{darkgreen}{\frac{13}{2x^2}}=\frac{2x^2(2+y)-13}{2x^2}$$

Показать решение

Скрыть

Представим многочлен $\textcolor{coral}{2+y}$ в виде дроби: $\textcolor{coral}{\frac{2+y}{1}}$.

Приведем дроби к общему знаменателю $\textcolor{orange}{2x^2}$ и выполним вычитание: $$\textcolor{coral}{\frac{2+y}{1}}-\frac{13}{2x^2}=\frac{(2+y)\cdot \textcolor{orange}{2x^2}}{1\cdot \textcolor{orange}{2x^2}}-\frac{13}{2x^2}=$$ $$=\frac{2x^2(2+y)-13}{2x^2}$$

Пример 2

Упростим выражение:$$\Big(\frac{3x+1}{3x-1}\overset{\textcolor{blue}{1}}-\frac{3x-1}{3x+1} \Big)\overset{\textcolor{coral}{2}}: \frac{6x}{15x-5}$$

$\textcolor{blue}{1)}$ Выполним действие в скобках:$$\frac{3x+1}{3x-1}-\frac{3x-1}{3x+1}=\frac{12x}{(3x-1)(3x+1)}$$

Показать решение

Скрыть

Приведем дроби к общему знаменателю $(\textcolor{purple}{3x-1})(\textcolor{orange}{3x+1})$:$$\frac{(3x+1) \cdot (\textcolor{orange}{3x+1})}{(3x-1)\cdot (\textcolor{orange}{3x+1})}-\frac{(3x-1)\cdot (\textcolor{purple}{3x-1})}{(3x+1)\cdot (\textcolor{purple}{3x-1})}=$$ $$=\frac{(3x+1)^2-(3x-1)^2}{(3x-1)(3x+1)}$$

В числителе распишем «разность квадратов»:$$(\textcolor{blue}{3x+1})^\textcolor{coral}{2}-(\textcolor{darkgreen}{3x-1})^\textcolor{coral}{2}=((\textcolor{blue}{3x+1})+(\textcolor{darkgreen}{3x-1}))((\textcolor{blue}{3x+1})-(\textcolor{darkgreen}{3x-1}))$$

Раскроем скобки и произведем вычисления:$$(\textcolor{lightblue}{3x}\cancel{+1}+\textcolor{lightblue}{3x}\cancel{-1})(\cancel{3x}+\textcolor{orange}{1}\cancel{-3x}+\textcolor{orange}{1})=\textcolor{lightblue}{6x}\cdot \textcolor{orange}{2}=12x$$

Получаем:$$\frac{12x}{(3x-1)(3x+1)}$$

$\textcolor{coral}{2)}$ Произведем деление:$$\frac{12x}{(3x-1)(3x+1)}:\frac{6x}{15x-5}=\frac{10}{3x+1}$$

Показать решение

Скрыть

Заменим деление умножением, а вторую дробь перевернем. В числителе второй дроби вынесем общий множитель $\textcolor{orange}{5}$ за скобки:$$\frac{\textcolor{purple}{12x}}{(\textcolor{darkgreen}{3x-1})(3x+1)} \cdot \frac{\textcolor{orange}{5}(\textcolor{darkgreen}{3x-1})}{\textcolor{purple}{6x}}$$

Сократим дроби на $\textcolor{darkgreen}{3x-1}$ и на $\textcolor{purple}{6x}$: $$\frac{2}{3x+1} \cdot \frac{5}{1}=\frac{10}{3x+1}$$

{"questions":,"placeholder":0,"answer":0}},"step":1,"hints":}]}

Представление в виде рациональной дроби

Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.

Пример 4

Представить в виде рациональной дроби a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a .

Решение

Данное выражение можно представить в виде a 2 — 25 a + 3 · 1 a 2 + 5 · a . Умножение выполняется в первую очередь по правилам.

Следует начать с умножения, тогда получим, что

a 2 — 25 a + 3 · 1 a 2 + 5 · a = a — 5 · (a + 5) a + 3 · 1 a · (a + 5) = a — 5 · (a + 5) · 1 (a + 3) · a · (a + 5) = a — 5 (a + 3) · a

Производим представление полученного результата с исходное. Получим, что

a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a — 3 — a — 5 a + 3 · a

Теперь выполняем вычитание:

a + 5 a · a — 3 — a — 5 a + 3 · a = a + 5 · a + 3 a · (a — 3) · (a + 3) — (a — 5) · (a — 3) (a + 3) · a · (a — 3) = = a + 5 · a + 3 — (a — 5) · (a — 3) a · (a — 3) · (a + 3) = a 2 + 3 · a + 5 · a + 15 — (a 2 — 3 · a — 5 · a + 15) a · (a — 3) · (a + 3) = = 16 · a a · (a — 3) · (a + 3) = 16 a — 3 · (a + 3) = 16 a 2 — 9

После чего очевидно, что исходное выражение примет вид 16 a 2 — 9 .

Ответ:
a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 — 9 .

Пример 5

Представить x x + 1 + 1 2 · x — 1 1 + x в виде рациональной дроби.

Решение

Заданное выражение записывается как дробь, в числителе которой имеется x x + 1 + 1 , а в знаменателе 2 · x — 1 1 + x . Необходимо произвести преобразования x x + 1 + 1 . Для этого нужно выполнить сложение дроби и числа. Получаем, что x x + 1 + 1 = x x + 1 + 1 1 = x x + 1 + 1 · (x + 1) 1 · (x + 1) = x x + 1 + x + 1 x + 1 = x + x + 1 x + 1 = 2 · x + 1 x + 1

Следует, что x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 x + 1 2 · x — 1 1 + x

Получившаяся дробь может быть записана как 2 · x + 1 x + 1: 2 · x — 1 1 + x .

После деления придем к рациональной дроби вида

2 · x + 1 x + 1: 2 · x — 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x — 1 = 2 · x + 1 · (1 + x) (x + 1) · (2 · x — 1) = 2 · x + 1 2 · x — 1

Можно решить это иначе.

Вместо деления на 2 · x — 1 1 + x производим умножение на обратную ей 1 + x 2 · x — 1 . Применим распределительное свойство и получаем, что

x x + 1 + 1 2 · x — 1 1 + x = x x + 1 + 1: 2 · x — 1 1 + x = x x + 1 + 1 · 1 + x 2 · x — 1 = = x x + 1 · 1 + x 2 · x — 1 + 1 · 1 + x 2 · x — 1 = x · 1 + x (x + 1) · 2 · x — 1 + 1 + x 2 · x — 1 = = x 2 · x — 1 + 1 + x 2 · x — 1 = x + 1 + x 2 · x — 1 = 2 · x + 1 2 · x — 1

Ответ:
x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 2 · x — 1 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Из курса алгебры школьной программы переходим к конкретике. В этой статье мы подробно изучим особый вид рациональных выражений – рациональные дроби
, а также разберем, какие характерные тождественные преобразования рациональных дробей
имеют место.

Сразу отметим, что рациональные дроби в том смысле, в котором мы их определим ниже, в некоторых учебниках алгебры называют алгебраическими дробями. То есть, в этой статье мы под рациональными и алгебраическими дробями будем понимать одно и то же.

По обыкновению начнем с определения и примеров. Дальше поговорим про приведение рациональной дроби к новому знаменателю и о перемене знаков у членов дроби. После этого разберем, как выполняется сокращение дробей. Наконец, остановимся на представлении рациональной дроби в виде суммы нескольких дробей. Всю информацию будем снабжать примерами с подробными описаниями решений.

Навигация по странице.

Сокращение простых рациональных дробей

Задача № 1

\

Первое, чему нам нужно научиться — выделять в исходных выражениях точные квадраты и более высокие степени, на основании которых мы сможем потом применять формулы. Давайте посмотрим:

\

\

Перепишем наше выражение с учетом этих фактов:

\

Ответ: $\frac{1}{3{{y}^{2}}-4x}$.

Задача № 2

Переходим ко второй задаче:

\

Упрощать тут нечего, потому что в числителе стоит константа, но я предложил эту задачу именно для того, чтобы вы научились раскладывать на множители многочлены, содержащие две переменных. Если бы вместо него был написанный ниже многочлен, как бы мы разложили его?

\

Давайте решим уравнение и найдем $x$, которые мы сможем поставить вместо точек:

\

\

\

\

\

Мы можем переписать трехчлен следующим образом:

\

С квадратным трехчленом мы работать научились — для этого и нужно было записать этот видеоурок. А что делать, если кроме $x$ и константы присутствует еще $y$? Давайте рассмотрим их как еще одни элементы коэффициентов, т.е. перепишем наше выражение следующим образом:

\

\

\

\

\

\

Запишем разложение нашей квадратной конструкции:

\

Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:

\

Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати

Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители

Нюансы решения

Запомните основные правила преобразования рациональных выражений:

• Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант.
• Работать нужно по такому алгоритму: когда мы смотрим и пытаемся выделить формулу сокращенного умножения, то, прежде всего, пытаемся все перевести в максимально возможную степень. После этого выносим за скобку общую степень.
• Очень часто будут встречаться выражения с параметром: в качестве коэффициентов будут возникать другие переменные. Их мы находим по формуле квадратного разложения.

Таким образом, как только вы видите рациональные дроби, первое, что нужно сделать — это разложить и числитель, и знаменатель на множители (на линейные выражения), при этом мы используем формулы сокращенного умножения или дискриминант.

Давайте посмотрим на пару таких рациональных выражений и попробуем их разложить на множители.