Построение графиков функций

Примеры задач и их решений на тему функций y=|x|, y=[x], y={x}, y=sign(x)

Найти значения функции y = |x| при x = -5, 0, 3.

Решение: Подставляем значения x в функцию y = |x|:

При x = -5: y = |-5| = 5
При x = 0: y = |0| = 0
При x = 3: y = |3| = 3
Ответ: y = 5, 0, 3.

Найти область определения функции y = {x}.

Решение: Фигурные скобки означают взятие дробной части числа, то есть y = x — . Область определения функции — все действительные числа.
Ответ: Область определения функции — все действительные числа.

Найти корни уравнения y = sign(x).

Решение: Функция y = sign(x) принимает значение -1 при x < 0, значение 0 при x = 0 и значение 1 при x > 0. Таким образом, уравнение y = sign(x) имеет два корня: x = -1 и x = 1.
Ответ: x = -1, 1.

Найти наибольшее и наименьшее значение функции y = {x} на отрезке .

Решение: Функция y = {x} принимает значения от 0 до 1 на интервале , от 1 до 2 на интервале , и т.д. Таким образом, на отрезке функция y = {x} принимает наибольшее значение 0.999… (бесконечно близкое к 1) в точке x = 5 и наименьшее значение 0 в точке x = 1.

Ответ: Наибольшее значение функции y = {x} на отрезке — 0.999…, наименьшее значение — 0.

Дробно-линейная функция

Теперь рассмотрим несколько более сложные ф-ции, чьи графики, однако, также представляют собой гиперболу. Пусть есть ф-ция вида

Как будет выглядеть ее график? Для ответа на этот вопрос выполним преобразование:

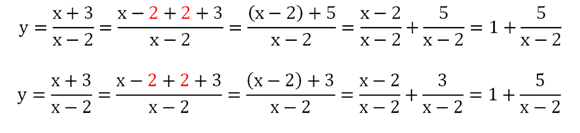
Здесь мы в числителе и знаменателе добавили и сразу вычли слагаемое 2.Этот прием помог нам выделить целую часть из дроби. В результате мы получили ф-цию, график которой можно получить с помощью двух параллельных переносов графика у = 6/х. Сначала график сместится на две единицы вправо:

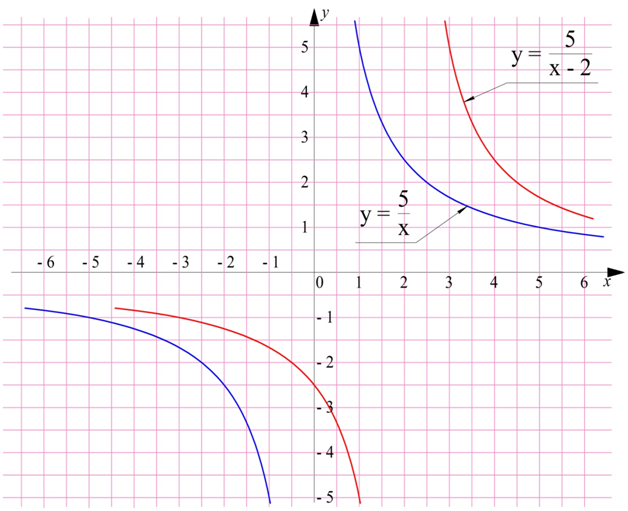
На следующем шаге график поднимется на единицу вверх:

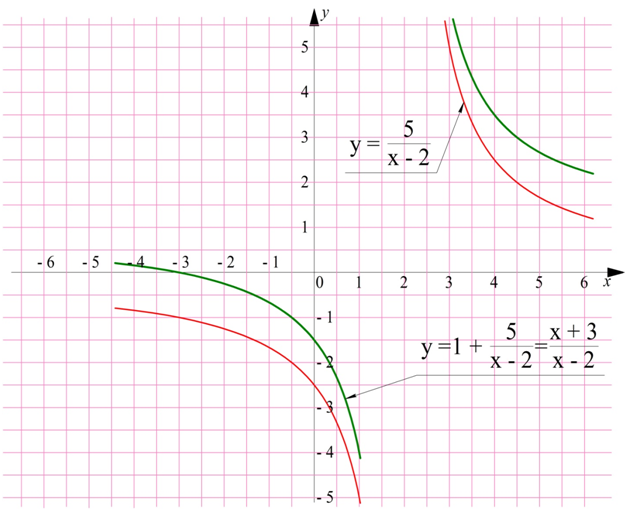
Стоит обратить внимание, что при таком передвижении гиперболы передвигаются и асимптоты графика гиперболы:

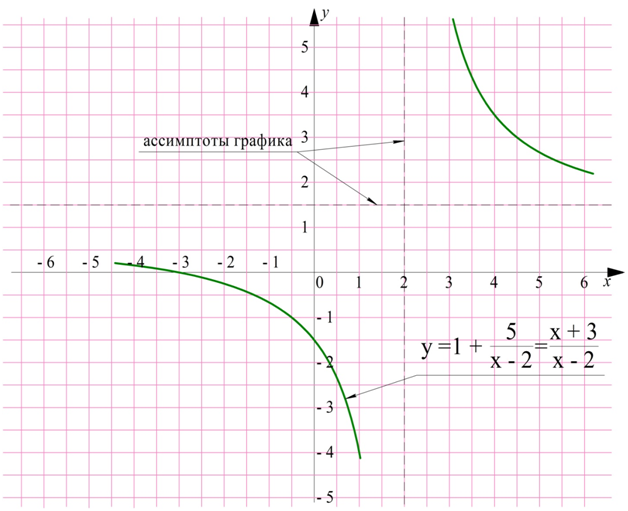
Функция

представляет собой дробь, являющуюся отношением двух линейных многочленов, х + 3 и х – 2. В математике подобные ф-ции называют дробно-линейными функциями. В качестве примеров дробно-линейных функций можно привести:

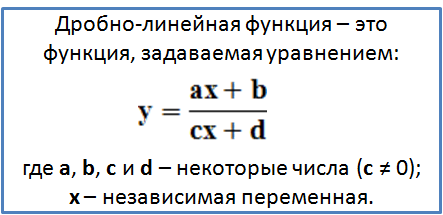
Из любой дробно-линейной функции можно выделить целую часть. Покажем это на нескольких примерах:

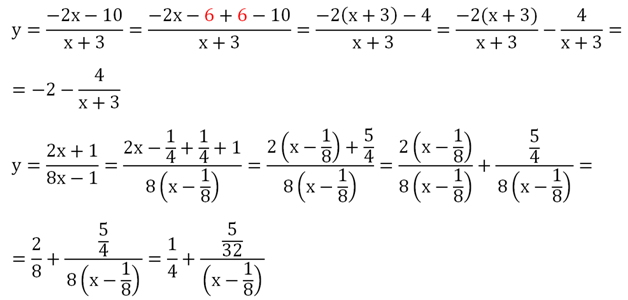
Во всех этих случаях график дробно-линейной функции можно построить с помощью двух параллельных переносов гиперболы.

Однако есть одно исключение. Иногда при выделении из дроби целой части дробной части не остается вовсе, то есть линейные полиномы можно сразу сократить. Например:

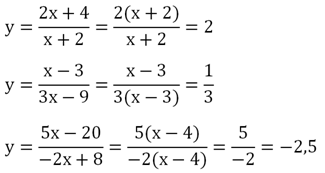
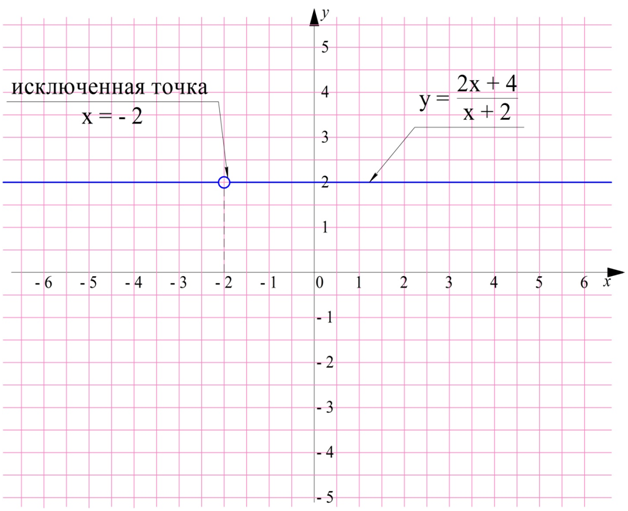
Графиком таких функций являются прямые горизонтальные линии. Однако на них должна быть одна «исключенная». Действительно, пусть надо построить график ф-ции

Проведя преобразования, получим

то есть у = 2. Однако в знаменателе дроби не может стоять ноль. Если же подставить в дробь х = – 2, то получим деление на ноль:

Поэтому график ф-ции будет выглядеть так:

Итак, по итогам урока мы узнали:

1. как растягиваются и сжимаются графики;
2. как графики функций переносятся вверх-вниз и влево-вправо;
3. что такое обратная пропорциональность и как выглядит ее график – гипербола;
4. как выглядит дробно-линейная функция, и каким образом ее график можно получить из гиперболы с помощью параллельных переносов.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

График логарифмической функции

Рассмотрим функцию с натуральным логарифмом .
Выполним поточечный чертеж:

Если позабылось, что такое логарифм, пожалуйста, обратитесь к школьным учебникам.

Основные свойства функции :

Область определения:

Область значений: .

Функция не ограничена сверху: , пусть и медленно, но ветка логарифма уходит вверх на бесконечность.
Исследуем поведение функции вблизи нуля справа: . Таким образом, ось  является вертикальной  асимптотой для графика функции при «икс» стремящемся к нулю справа.

Обязательно нужно знать и помнить типовое значение логарифма: .

Принципиально так же выглядит график логарифма при основании : , ,  (десятичный логарифм по основанию 10) и т.д. При этом, чем больше основание, тем более пологим будет график.

Случай  рассматривать не будем, что-то я не припомню, когда последний раз строил график с таким основанием. Да и логарифм вроде  в задачах высшей математики ооочень редкий гость.

В заключение параграфа скажу еще об одном факте: Экспоненциальная функция  и логарифмическая функция  – это две взаимно обратные функции. Если присмотреться к графику логарифма, то можно увидеть, что это – та же самая экспонента, просто она расположена немного по-другому.

Примеры применения функций

Функции y = |x|, y = , y = {x} и y = sign(x) находят применение во многих областях науки, техники и экономики. Например, функция y = |x| используется в физике для описания модуля вектора или амплитуды волн. Она также широко применяется в экономике для описания абсолютной величины изменений величин.

Функция y = , называемая функцией целой части, используется в комбинаторике и теории чисел для округления вниз до ближайшего целого числа. Она также может быть использована в экономических моделях для округления до целого числа, например, при расчете налогов.

Функция y = {x}, называемая функцией дробной части, используется в комбинаторике, теории чисел и теории вероятностей. Она также может быть использована в физике и технике при работе с периодическими сигналами и в криптографии для генерации случайных чисел.

Функция y = sign(x), называемая функцией знака, используется в анализе сигналов и теории управления для определения направления движения сигнала или системы. Она также может быть использована в физике и механике для определения направления движения тела.

В целом, функции y = |x|, y = , y = {x} и y = sign(x) являются важными и полезными математическими инструментами для решения различных задач в различных областях науки, техники и экономики.

Что такое функция в математике

Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.

Сколько времени двигается автомобиль	Сколько км проедет автомобиль
1 час	60 км
2 часа	120 км
3 часа	180 км

Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.

Обозначим за « x » время автомобиля в пути.

Обозначим за « y » расстояние, пройденное автомобилем.

Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).

Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.

Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».

Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:

Функцией называют зависимость « y » от « x ».

Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.

Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.

Примеры других функций:

Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: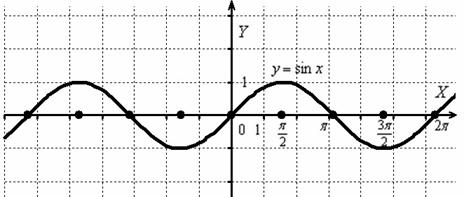
Согласно правилу, при  график сохраняется: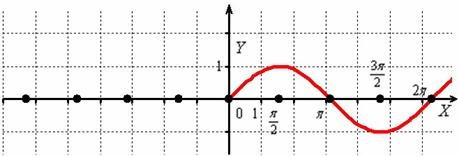
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: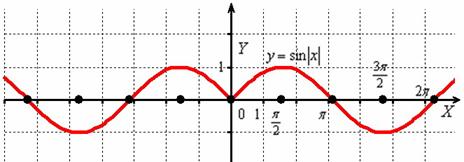

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: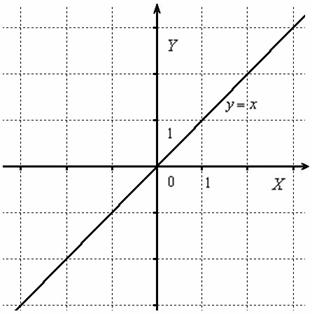
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: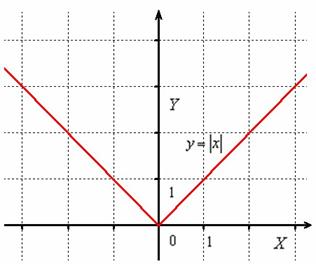

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)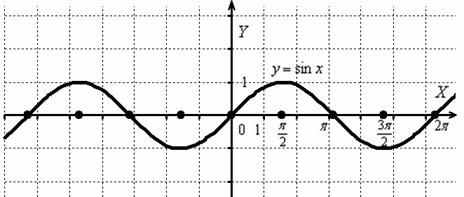

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :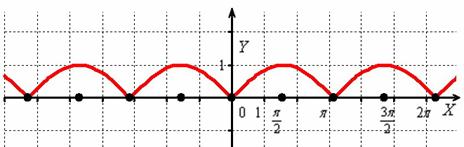

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем:, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)

Квадратичные

В функциях такого типа обязательным параметром является возведение x во вторую степень. В общем виде формула выражается уравнением:

\

Одной из особенностей такого выражения является невозможность появления в третьей и четвертой четверти без дополнительных коэффициентов . В зависимости от наличия дополнительных действий сложения и вычитания, график может быть повернут как вверх, так и вниз. Однако в любом случае он будет представлять собой дугу, которая в математике называется параболой

Также стоит обратить внимание, что самой нижней точке параболы является так называемая вершина. Находится же она с помощью специальной формулы:

\

Подставив x в формулу параболы, находим значение координаты y.Для того чтобы построить такой график, необходимо знать как минимум 5 точек — координаты вершины параболы и по 2 точки на каждой из двух дуг. В частном случае, когда а=1, а b=0, имеем формулу y=x2. В этом случае вершину находить нет необходимости, так как она будет находиться в точке отсчета (0; 0) (рис.2).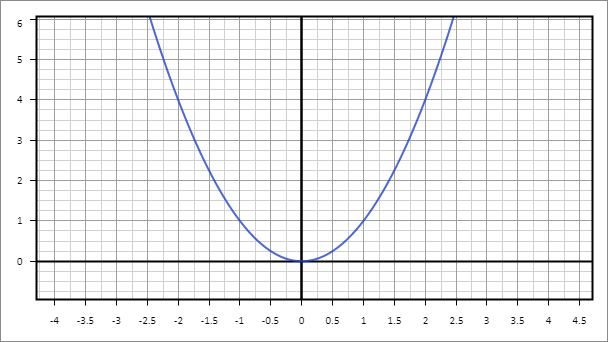
Рис. 2. Изображение формулы y=x2

Свойства и графики функции корень

В общем виде это функция ,
где n — натуральное число больше единицы.

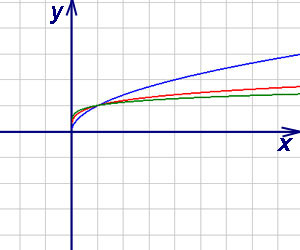
Корень n-й степени, n — чётное число

Область определения: .

Область значений: .

Функция возрастает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция выпуклая на всей области определения.

Это непериодическая функция.

График функции полностью расположен в первом квадранте координатной плоскости.

На рисунке синим цветом изображён график функции ,
красным — ,
зелёным — .

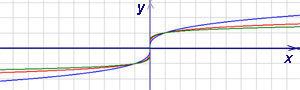
Корень n-й степени, n — нечётное число

Область определения: множество всех действительных
чисел .

Область значений: множество всех действительных
чисел .

Функция возрастает на всей области определения.

Функция является нечётной.

Функция выпуклая на и
вогнутая на .

Это непериодическая функция.

Ветви графика функции расположены в первом и третьем квадрантах координатной плоскости.

На рисунке синим цветом изображён график функции ,
красным — ,
зелёным — .

Логарифмическая функция.

Следующей основной элементарной функцией является логарифмическая функция , где , . Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при .

График логарифмической функции принимает различный вид в зависимости от значения основания а.

Начнем со случая, когда .

Для примера приведем графики логарифмической функции при а = 1/2 – синяя линия, a = 5/6 – красная линия. При других значениях основания, не превосходящих единицы, графики логарифмической функции будут иметь схожий вид.

Свойства логарифмической функции с основанием меньшим единицы.

• Область определения логарифмической функции: . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
• Область значений: .
• Функция не является ни четной, ни нечетной, то есть она общего вида.
• Логарифмическая функция убывает на всей области определения.
• Функция вогнутая при .
• Точек перегиба нет.
• Горизонтальных асимптот нет.
• Функция проходит через точку (1;0).

Перейдем к случаю, когда основание логарифмической функции больше единицы ().

Покажем графики логарифмических функций – синяя линия, – красная линия. При других значениях основания, больших единицы, графики логарифмической функции будут иметь схожий вид.

Свойства логарифмической функции с основанием большим единицы.

• Область определения: . При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
• Областю значений логарифмической функции является все множество действительных чисел, то есть, интервал .
• Функция не является ни четной, ни нечетной, то есть она общего вида.
• Функция возрастает при .
• Функция выпуклая при .
• Точек перегиба нет.
• Горизонтальных асимптот нет.
• Функция проходит через точку (1;0).

Параллельный перенос графиков функций

Теперь посмотрим, как передвинется отдельная точка на координатной плоскости, если к ее ординате добавить какое-нибудь число. Если это число положительное, то точка поднимется выше, а если отрицательное, то она опустится:

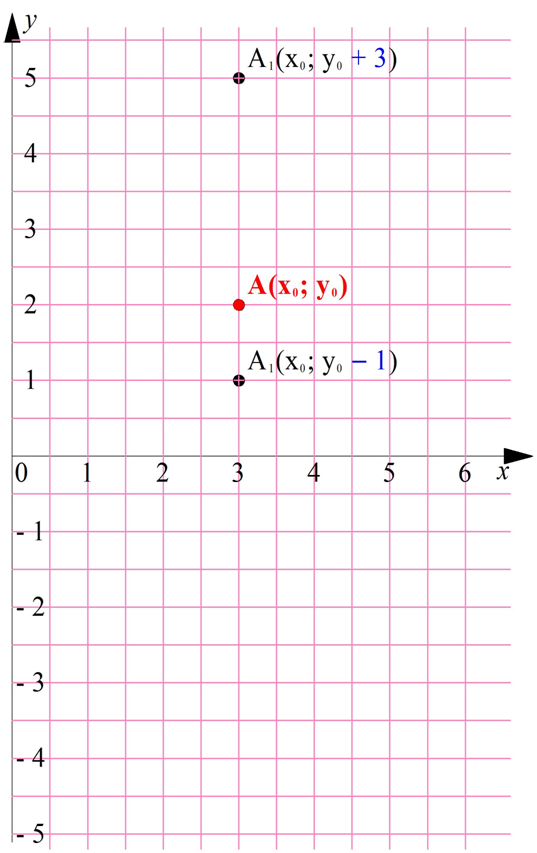
Это означает, что если к какой-нибудь функции добавить некоторое число, то график функции переместится вверх или вниз. Для примера построим графики функций у = х2 + 2 и у = х2 – 5:

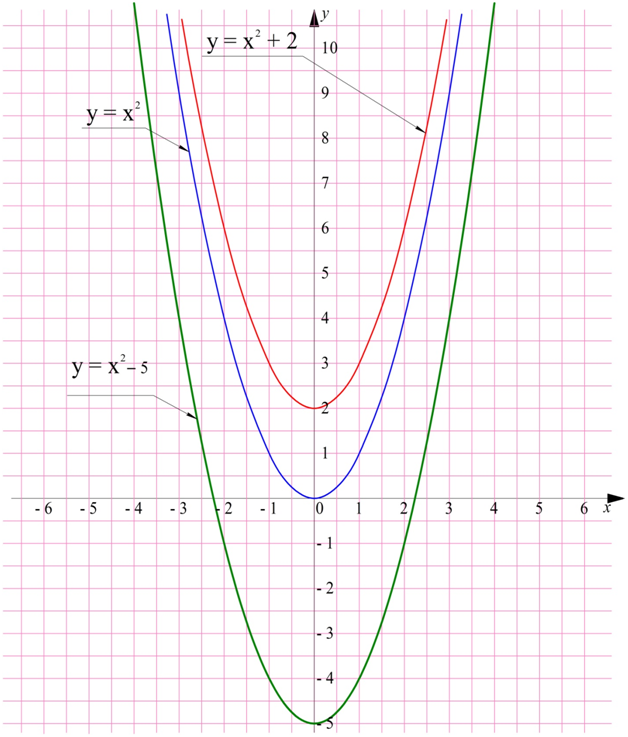
График у = х2 + 2 представляет собой тот же график у = х2, то есть параболу, который подняли на две единицы вверх. График у = х2 – 5 получен за счет сдвига вниз на 5 единиц этой же параболы. Подобное перемещение называют параллельным переносом графика функции.

Параллельный перенос возможен не только в вертикальном, но и в горизонтальном направлении. Для такого перемещения надо изменить абсциссу точки, а не ординату:

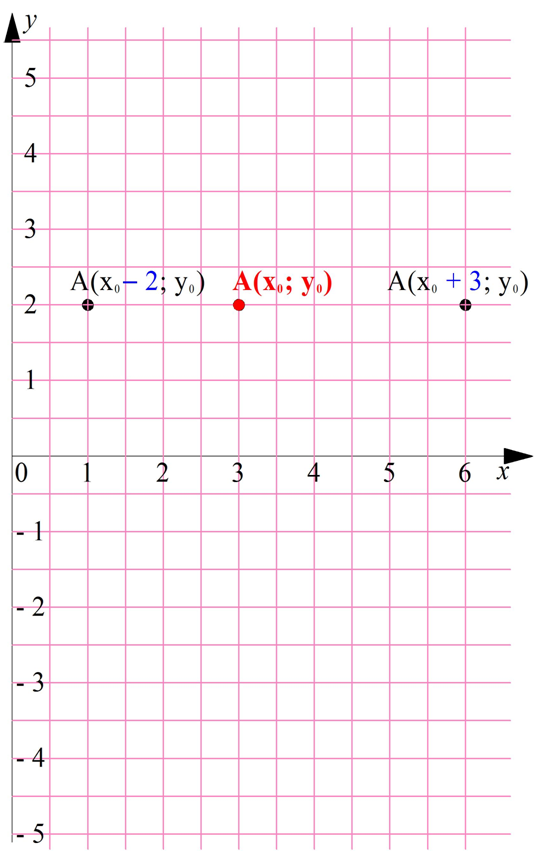
Аналогично может сдвинуться не только точка, но и целый график функции. Если вместо аргумента х подставить в ф-цию величину (х +n), то график сместится на n единиц влево.

Проиллюстрируем это с помощью ф-ций у = х2 и g = (х + 3)2. Будем вычислять значения обеих ф-ций в некоторых точках, причем для функции g будем брать значения х, меньше на три единицы:

у(0) = 02 = 0 и g(– 3) = g(– 3 + 3)2 = 02 = 0

у(– 1) = (– 1)2 = 1 и g(– 4) = g(– 4 + 3)2 = (– 1)2 = 1

у(– 2) = (– 2)2 = 4 и g(– 5) = g(– 5 + 3)2 = (– 2)2 = 4

Видно, что одинаковые значения ф-ции принимают тогда, когда аргумент у ф-ции g меньше на 3. Это значит что если сместить точку графика у = х2 на 3 единицы влево, по она попадает на график g = (х + 3)2.

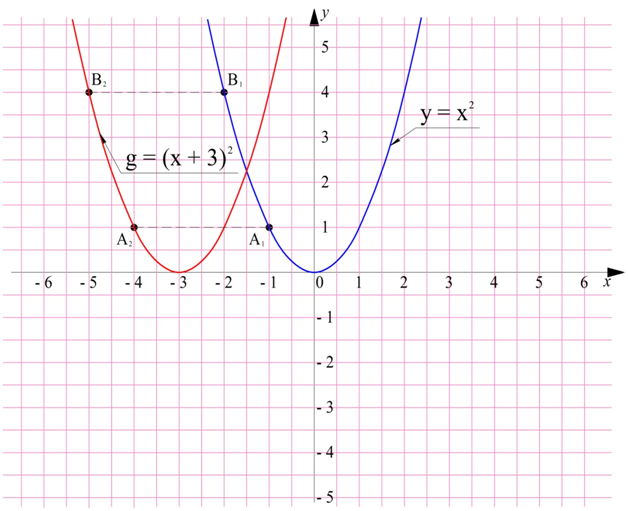
Точка А₁ сдвинулась влево на 3 единицы и перешла в точку А₂. Аналогично точка В₁ отобразилась в точку В₂.

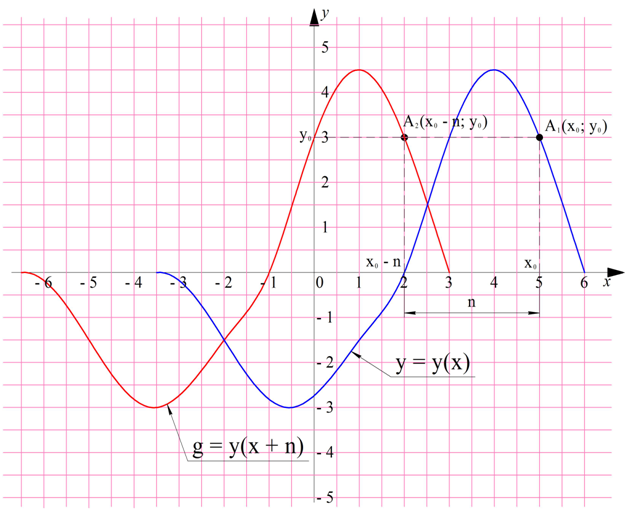
Пусть в общем случае есть функции у = у(х) и g(x) = у(х +n), где n – некоторое постоянное число. Значение у(х) в точке х обозначается как у. Теперь найдем значение g(x) в точке (х – n):

g(х–n) = у(х –n+n) = y(x).

Получили, то же самое значение, что и у у(х). Покажем это на рисунке:

Рассмотрим теперь случай, когда график сдвигается вправо. Для этого из аргумента исходной функции надо вычесть какое-то число. На рисунке показаны графики функций у = 2х и у = 2(х – 4):

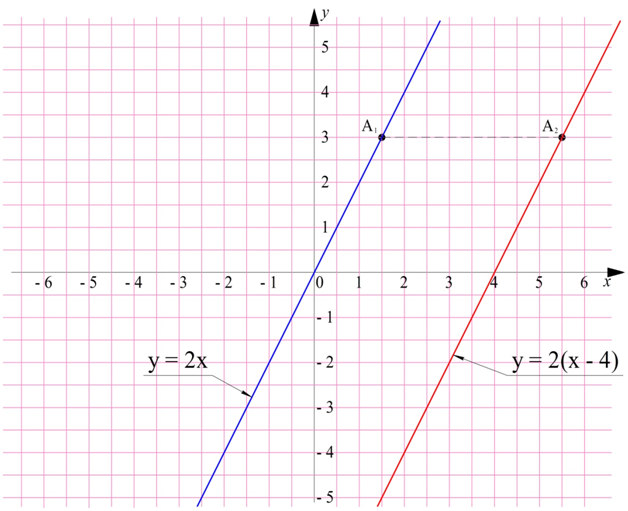
Каждая точка исходного графика (например, А₁) «переехала» на 4 единицы вправо.

Надо понимать, что иногда один график можно получить из другого в несколько переходов. Пусть надо построить график у = – (х – 4)2 + 5. Его можно получить из обычной параболы у = х2 в три шага.

Сперва строим график у = (х – 4)2. Вершина параболы, как и все остальные точки, сместится на 4 позиции вправо:

Далее построим график у = – (х – 4)2. Для этого его надо отобразить симметрично относительно оси Ох (ось симметрии параболы не сдвигается, но ее ветви будут направлены вниз, а не вверх):

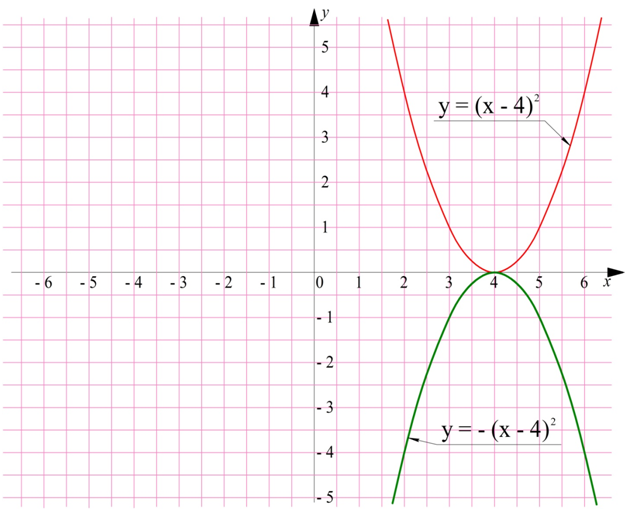
Последний шаг – это построение графика у = – (х – 4)2 + 5. Его можно получить, подняв предыдущий график на 5 единиц вверх:

Урок алгебры в 7 классе по теме:»Что такое функция?»

Выбранный для просмотра документ pril1(2).ppt

Описание презентации по отдельным слайдам:

Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины: зависимая переменная и независимая переменная (аргумент функции и значение функции). Узнать способы задания функции. Закрепить их при решении задач

Понятие функции можно считать стержнем, вокруг которого группируется преподавание математики Никакое другое понятие не отражает явлений реальной действительности с такой с такой конкретностью, как понятие функциональной зависимости

Ключевое слово урока: зависимость

Первый пример зависимости одной величины от другой (с помощью формулы) Площадь квадрата зависит от длины его стороны. Если изменить длину стороны квадрата, то изменится и значение площади. S = aa Если а=3, то S=3*3=9(ед кв) Если а=0,4, то S=0,4*0,4 = 0,16(ед кв) 3 0,4

Другие примеры зависимостей Периметр квадрата зависит от длины его стороны Длина окружности зависит от длины его радиуса Пройденный путь зависит от его скорости Длина стального стержня зависит от его температуры Давление масла зависит от высоты столба масла Ваши примеры

а (длина стороны) Аргумент функции Независимая переменная S (значение площади) Значение функции Зависимая переменная

Второй пример зависимости одной величины от другой (табличный): В таблице показана зависимость количества выпущенных заводом электроплит от порядкового номера месяца, в котором были выпущены электроплиты х 1 2 3 4 5 6 у 230 270 310 300 360 340

Третий пример зависимости одной величины от другой ( с помощью графика)

Что же такое функция? Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению х соответствует единственное значение у

Задание №1. Среди данных линий найти такие, которые являются графиками какой-либо функции игрек от икс, тот есть у которых каждому значению икс соответствует не более одного значения игрек

Задание №2. Среди данных таблиц найти такую, которая является функцией у от х. то есть каждому значению х соответствует не более одного значения у х 1 1 2 у 3 4 5 Х 3 6 3 у 2 4 9 Х 1 2 3 у 4 4 5

Домашнее задание (записать в дневники) Читать П 10, стр 39 – 41 ( до последнего определения), выучить определение функции и значения новых терминов №252, № 255,№ 188(а) Желающие находят дополнительный материал по теме «История появления понятия «функция»

Выбранный для просмотра документ Тема урока.doc

Схема для построения графика функции

1. Область определения $D(f)$ и область значения $E(f)$.
2. Четность ($f\left(x\right)=f\left(-x\right))$, нечетность ($f\left(x\right)=-f\left(x\right))$, периодичность ($f\left(x\right)=f\left(x+T\right))$.

3. Точки пересечения с осями координат и промежутки, где $f\left(x\right)>0$ и $f\left(x\right)

4. Исследовать на возрастание ${(f}’\left(x\right)>0)$, убывание ${(f}’\left(x\right)

5. Исследовать на точки перегиба и интервалы выпуклости $(f^{»}\left(x\right) > 0)$, вогнутости ($f^{»}\left(x\right)

6. Вычислить пределы на границах области определения.
7. Значения в дополнительных точках.
8. График.

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции \(y=x^2, \ y=|x|^{3/2}, \ y=\sin^3{3x}\) заданы на множестве \(\mathbb{R}\) аналитически.

Если числовая функция f задана формулой и не указана область ее определения \(D(f)\) , то принято считать, что \(D(f)\) — множество всех тех значений аргумента, при которых эта формула имеет смысл, и результатом каждой операции, указанной в формуле, является вещественное число. Например, если \(f(x)=\sqrt{9-x^2}\), то \(D(f)=\), а если \(f(x)=\sqrt{\operatorname{lg} \sin{x}}\), то \(D(f)\) — множество корней уравнения \(\sin x=1\) то есть множество чисел \(x_{k}=\pi/2.+2\pi k\), где \(k\in Z\).

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=\left\{\begin{array}{l}-x,\quad если\;x\;<\;0,\\x^{2},\quad если\;0\leq x\leq1,\\2-\sqrt{x},\quad если\;x>1,\end{array}\right.\nonumber
$$
задана аналитическим способом на \(\mathbb{R}\) с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

График показательной функции

В данном параграфе я сразу рассмотрю экспоненциальную функцию , поскольку в задачах высшей математики в 95% случаев встречается именно экспонента.

Напоминаю, что  – это иррациональное число: , это потребуется при построении графика, который, собственно, я без церемоний и построю. Трёх точек, пожалуй, хватит:

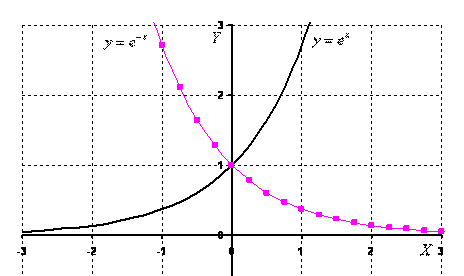
График функции  пока оставим в покое, о нём позже.

Основные свойства функции :

Область определения:  – любое «икс».

Область значений:

Обратите внимание, что ноль не включается в область значений. Экспонента – функция положительная, то есть для любого «икс» справедливо неравенство , а сам график экспоненты полностью расположен в верхней полуплоскости

Функция не ограничена сверху: , то есть, если мы начнем уходить по оси  вправо на плюс бесконечность, то соответствующие значения «игрек» стройным шагом будут тоже уходить вверх на  по оси  . Кстати, график экспоненциальной функции будет «взмывать» вверх на бесконечность очень быстро и круто, уже при   

Исследуем поведение функции на минус бесконечности: . Таким образом, ось  является горизонтальной асимптотой для графика функции , если Принципиально такой же вид имеет любая показательная функция , если . Функции , ,  будут отличаться только крутизной наклона графика, причем, чем больше основание, тем круче будет график.

Обратите внимание, что во всех случаях графики проходят через точку , то есть. Это значение должен знать даже «двоечник»

Теперь рассмотрим случай, когда основание . Снова пример с экспонентой  – на чертеже соответствующий график прочерчен малиновым цветом? Что произошло? Ничего особенного – та же самая экспонента, только она «развернулась в другую сторону». Об этой метаморфозе можно получить подробную информацию в статье Построение графиков с помощью геометрических преобразований.

Принципиально так же выглядят графики функций ,  и т. д.

Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.

Общая схема построения графика функциис помощью геометрических преобразований

Рассмотрим функцию , которая «базируется» на некоторой функции . Для многих читателей алгоритм построения графика уже понятен:

– на первом шаге выполняем преобразования, связанные с АРГУМЕНТОМ функции (см. первые два параграфа), в результате чего получаем график функции ;

– на втором шаге выполняем только что рассмотренные преобразования, связанные с самой ФУНКЦИЕЙ, и получаем график .

Завершим самое длинное построение данного урока:

Пример 19 (концовка Примера 10)

Построить график функции

В примере № 10 мы выполнили построение графика , то есть полностью разобрались с аргументом функции. И сейчас осталось выполнить завершающие шаги.

График функции :

4) отобразим симметрично относительно оси : ;
5) сдвинем вдоль оси  на 3 единицы вверх: :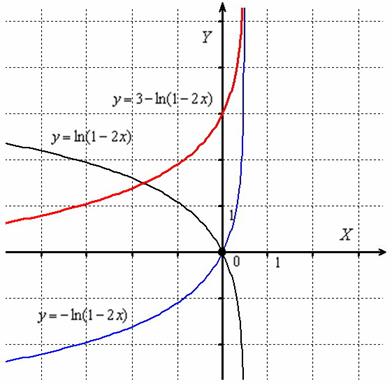

На практике, к счастью, построения почти всегда более коротки, например:

 – кубическую параболу  сдвигаем вдоль оси  на 5 единиц вправо и сжимаем вдоль оси  в 3 раза.

 – график экспоненты отображаем симметрично относительно оси ординат, затем – симметрично относительно оси абсцисс.

 – график функции  смещаем влево на 5 единиц, затем – вверх на 1 единицу.

И т.д. Некоторые геометрические преобразования можно поменять местами, но это возможно далеко не всегда! Поэтому «чайникам» лучше придерживаться алгоритма, изложенного в начале параграфа.

Весь материал статьи, который носит в бОльшей степени всё-таки справочный характер, потребуется для выполнения чертежей в других задачах, но время от времени на практике рассматриваемое задание встречается отдельно, причём, бывает, в «сыром» виде:

Пример 20

Построить график функции  с помощью преобразований графиков элементарных функций

Методику быстрого построения параболы я разобрал на первом уроке о графиках функций, однако здесь по условию необходимо применить вполне определённый способ.

На первом шаге представим функцию в виде . Для этого используем так называемый метод выделения полного квадрата. Советую не пренебрегать задачей, поскольку типовой приём потребуется и в будущем, например, при нахождении интегралов от некоторых дробей.

Идея состоит в том, чтобы искусственно преобразовать функцию ТАК, чтобы воспользоваться одной из формул сокращенного умножения  либо .

Начнём преобразования. Коэффициент при  выносим за скобку:
Очевидно, что выражение сведётся к формуле . В скобках конструируем :
Таким образом, . Теперь организуем , для этого в скобках прибавим и вычтем :
Последнее слагаемое выносим из скобок:
Используем формулу  и суммируем два последних слагаемых:

В целях проверки целесообразно раскрыть скобки и убедиться, что получится исходная функция:

Построим график . Параболу :

1) Сдвинем вдоль оси  на  влево:  (синий цвет);
2) Вытянем вдоль оси  в 2 раза:  (малиновый цвет);
3) Сдвинем вдоль оси  на  вверх:  (красный цвет):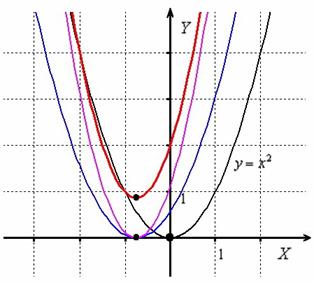

Рассмотрим ещё один типовой трюк:

Пример 21

Построить график функции  с помощью преобразований графиков элементарных функций.

Сначала сведём функцию к виду . Все действия я закомментирую:

(1) В знаменателе выносим –1 за скобки. Это необходимо, чтобы аргумент функции представить «в привычном» порядке .
(2) Минус знаменателя поставим перед дробью. В числителе проведём искусственное преобразование – прибавим и вычтем единицу. Это необходимо для почленного деления на следующем шаге.
(3) Почленно делим числитель на знаменатель. Возьмите на заметку рассмотренный приём, он используется при интегрировании дробей.
(4) Раскрываем скобки.

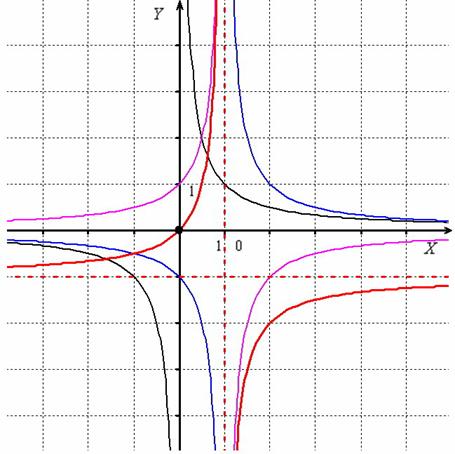
Проведём построение. График гиперболы  (чёрный цвет):

1) Сдвинем вправо на 1 единицу:  (синий цвет);
2) Отобразим симметрично относительно оси абсцисс:  (малиновый цвет);
3) Сдвинем вдоль оси  на единицу вниз:  (красный цвет):

Перейдём к заключительной части урока, в которой речь пойдёт о модуле. Хотел её сделать отдельной небольшой страничкой или pdf-кой, да потом передумал, чего уж тут мелочиться. Хотя эта статья далеко не рекордная по количеству букв, солидную часть объема занимают чертежи.

Тригонометрические функции, их свойства и графики.

Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.

Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т — период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.

Теперь разберемся со всеми тригонометрическими функциями по порядку.

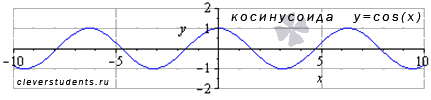
Функция синус y = sin(x).

Изобразим график функции синус, его называют «синусоида».

Свойства функции синус y = sinx.

• Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
• Наименьший положительный период функции синуса равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
• Функция синус — нечетная, так как .
• Функция убывает при ,
  возрастает при .
• Функция синус имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция y = sinx вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

Функция косинус y = cos(x).

График функции косинус (его называют «косинусоида») имеет вид:

Свойства функции косинус y = cosx.

• Область определения функции косинус: .
• Наименьший положительный период функции y = cosx равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
• Функция косинус — четная, так как .
• Функция убывает при ,
  возрастает при .
• Функция y = cosx имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

Функция тангенс y = tg(x).

График функции тангенс (его называют «тангенсоида») имеет вид:

Свойства функции тангенс y = tgx.

• Область определения функции тангенс: , где , Z – множество целых чисел.
  Поведение функции y = tgx на границе области определения
  Следовательно, прямые , где , являются вертикальными асимптотами.
• Наименьший положительный период функции тангенс .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции y = tgx: .
• Функция тангенс — нечетная, так как .
• Функция возрастает при .
• Функция вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.

Функция котангенс y = ctg(x).

Изобразим график функции котангенс (его называют «котангенсоида»):

Свойства функции котангенс y = ctgx.

• Область определения функции котангенс: , где , Z – множество целых чисел.
  Поведение на границе области определения
  Следовательно, прямые , где являются вертикальными асимптотами.
• Наименьший положительный период функции y = ctgx равен пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции котангенс: .
• Функция нечетная, так как .
• Функция y = ctgx убывает при .
• Функция котангенс вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.