Свойства степеней, формулировки, доказательства, примеры

Степень с натуральным показателем, квадрат числа, куб числа

Для начала дадим определение степени числа с натуральным показателем. Забегая вперед, скажем, что определение степени числа a с натуральным показателем n дается для действительного числа a, которое будем называть основанием степени, и натурального числа n, которое будем называть показателем степени. Также отметим, что степень с натуральным показателем определяется через произведение, так что для понимания нижеизложенного материала нужно иметь представление об умножении чисел.

Определение.

Степень числа a с натуральным показателем n — это выражение вида an, значение которого равно произведению n множителей, каждый из которых равен a, то есть, .
В частности, степенью числа a с показателем 1 называется само число a, то есть, a1=a.

Из данного определения понятно, что с помощью степени с натуральным показателем можно кратко записывать произведения нескольких одинаковых множителей. Например, 8·8·8·8 можно записать как степень 84. Это аналогично тому, как с помощью произведения записывается сумма одинаковых слагаемых, к примеру, 8+8+8+8=8·4 (смотрите статью общее представление об умножении натуральных чисел).

Сразу стоит сказать о правилах чтения степеней. Универсальный способ чтения записи an таков: «a в степени n». В некоторых случаях также допустимы такие варианты: «a в n-ой степени» и «n-ая степень числа a». Для примера возьмем степень 812, это «восемь в степени двенадцать», или «восемь в двенадцатой степени», или «двенадцатая степень восьми».

Вторая степень числа, а также третья степень числа имеют свои названия. Вторую степень числа называют квадратом числа, например, 72 читается как «семь в квадрате» или «квадрат числа семь». Третья степень числа называется кубом числа, к примеру, 53 можно прочитать как «пять в кубе» или сказать «куб числа 5».

Пришло время привести примеры степеней с натуральными показателями. Начнем со степени 57, здесь 5 – основание степени, а 7 – показатель степени. Приведем еще пример: десятичная дробь 4,32 является основанием, а натуральное число 9 – показателем степени (4,32)9.

Обратите внимание, что в последнем примере основание степени 4,32 записано в скобках: чтобы избежать разночтений мы будем брать в скобки все основания степени, которые отличны от натуральных чисел. В качестве примера приведем следующие степени с натуральными показателями , их основания не являются натуральными числами, поэтому они записаны в скобках

Ну и для полной ясности в этом моменте покажем разницу, заключенную в записях вида (−2)3 и −23. Выражение (−2)3 – это степень отрицательного числа −2 с натуральным показателем 3, а выражение −23 (его можно записать как −(23)) соответствует числу, противоположному значению степени 23.

Заметим, что встречается обозначение степени числа a с показателем n вида a^n. При этом, если n – многозначное натуральное число, то показатель степени берется в скобки. Например, 4^9 – это другая запись степени 49. А вот еще примеры записи степеней при помощи символа «^»: 14^(21), (−2,1)^(155). В дальнейшем мы преимущественно будем пользоваться обозначением степени вида an.

Данное выше определение позволяет находить значение степени с натуральным показателем. Для этого нужно вычислить произведение n одинаковых множителей, равных a. Эта тема заслуживает детального рассмотрения в отдельной статье – смотрите .

Одной из задач, обратной возведению в степень с натуральным показателем, является задача нахождения основания степени по известному значению степени и известному показателю. Эта задача приводит к понятию корня из числа.

Также стоит изучить , которые вытекают из данного определения степени и свойств умножения.

Что такое степенные выражения?

Термин «степенные выражения» практически не встречается школьных учебниках математики, но он довольно часто фигурирует в сборниках задач, особенно предназначенных для подготовки к ЕГЭ и ОГЭ, например, . После анализа заданий, в которых требуется выполнить какие-либо действия со степенными выражениями, становится понятно, что под степенными выражениями понимают выражения, содержащие в своих записях степени. Поэтому, для себя можно принять такое определение:

Определение.

Степенные выражения – это выражения, содержащие степени.

Приведем примеры степенных выражений. Причем будем их представлять согласно тому, как происходит развитие взглядов на степень числа от степени с натуральным показателем до степени с действительным показателем.

Как известно, сначала происходит знакомство со степенью числа с натуральным показателем, на этом этапе появляются первые самые простые степенные выражения типа 32, 75+1, (2+1)5, (−0,1)4, , 3·a2−a+a2, x3−1, (a2)3 и т.п.

Дальше вводится нулевая степень числа, и начинают встречаться выражения, содержащие степени с нулевым показателем, например, 5, (a+1), 3+52−3,2, …

Чуть позже изучается степень числа с целым показателем, что приводит к появлению степенных выражений с целыми отрицательными степенями, наподобие следующих: 3−2, , a−2+2·b−3+c2.

В старших классах вновь возвращаются к степеням. Там вводится степень с рациональным показателем, что влечет появление соответствующих степенных выражений: , , и т.п. Наконец, рассматриваются степени с иррациональными показателями и содержащие их выражения: , .

Перечисленными степенными выражениями дело не ограничивается: дальше в показатель степени проникает переменная, и возникают, например, такие выражения 2×2+1 или . А после знакомства с логарифмом, начинают встречаться выражения со степенями и логарифмами, к примеру, x2·lgx−5·xlgx.

Итак, мы разобрались с вопросом, что представляют собой степенные выражения. Дальше будем учиться преобразовывать их.

Примеры преобразований выражений, содержащих степень с дробным показателем

Рассмотрим несколько примеров, демонстрирующих применение этих свойств для преобразования выражений.

1. Вычислить 7 (1/4) * 7 (3/4) .

7 (1/4) * 7 (3/4) = z (1/4 + 3/4) = 7.

2. Вычислить 9 (2/3) : 9 (1/6) .

9 (2/3) : 9 (1/6) = 9 (2/3 — 1/6) = 9 (1/2) = √9 = 3.

3. Вычислить (16 (1/3)) (9/4) .

(16 (1/3)) (9/4) = 16 ((1/3)*(9/4)) =16 (3/4) = (2 4) (3/4) = 2 (4*3/4) = 2 3 = 8.

4. Вычислить 24 (2/3) .

24 (2/3) = ((2 3)*3) (2/3) = (2 (2*2/3))*3 (2/3) = 4*3√(3 2)=4*3√9.

5. Вычислить (8/27) (1/3) .

(8/27) (1/3) = (8 (1/3))/(27 (1/3)) = ((2 3) (1/3))/((3 3) (1/3))= 2/3.

6. Упростить выражение ((a (4/3))*b + a*b (4/3))/(3√a + 3√b)

((a (4/3))*b + a*b (4/3))/(3√a + 3√b) = (a*b*(a (1/3) + b (1/3)))/(1/3) + b (1/3)) = a*b.

7. Вычислить (25 (1/5))*(125 (1/5)).

(25 (1/5))*(125 (1/5)) =(25*125) (1/5) = (5 5) (1/5) = 5.

8. Упростить выражение

• (a (1/3) — a (7/3))/(a (1/3) — a (4/3)) — (a (-1/3) — a (5/3))/(a (2/3) + a (-1/3)).
• (a (1/3) — a (7/3))/(a (1/3) — a (4/3)) — (a (-1/3) — a (5/3))/(a (2/3) + a (-1/3)) =
• = ((a (1/3))*(1-a 2))/((a (1/3))*(1-a)) — ((a (-1/3))*(1-a 2))/ ((a (-1/3))*(1+a)) =
• = 1 +a — (1-a) = 2*a.

Как видите используя эти свойства, можно значительно упростить некоторые выражения, которые содержат степени с дробными показателями.

Тема: «Преобразование выражений, содержащих степени с дробным показателем»

“Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь”. (М.В.Ломоносов)

Цели урока:

образовательные:
обобщить и систематизировать знания учащихся по теме “Степень с рациональным показателем”;проконтролировать уровень усвоения материала;ликвидировать пробелы в знаниях и умениях учащихся;

развивающие:
формировать навыки самоконтроля учащихся;создать атмосферу заинтересованности каждого ученика в работе, развивать познавательную активность учащихся;

воспитательные:
воспитывать интерес к предмету, к истории математики.

Тип урока: урок обобщения и систематизации знаний

Оборудование: оценочные листы, карточки с заданиями, дешифраторами, кроссвордами для каждого учащегося.

Предварительная подготовка: класс разбит на группы, в каждой группе руководитель — консультант.

ХОД УРОКА

I. Организационный момент.

Учитель:
Мы закончили изучение темы “Степень с рациональным показателем и её свойства”. Ваша задача на этом уроке, показать, как вы усвоили изученный материал и как вы умеете применять полученные знания при решении конкретных задач. На столе у каждого из вас есть оценочный лист. В него вы будете вносить свою оценку за каждый этап урока. В конце урока вы выставите средний балл за урок.

Оценочный лист

	Кроссворд	Разминка	Работа втетради	Уравнения	Проверь себя (с\р)

II. Проверка домашней работы.

Взаимопроверка с карандашом в руках, ответы зачитываются учащимися.

III
. Актуализация знаний учащихся.

Учитель:
Известный французский писатель Анатоль Франс сказал в свое время: “Учиться надо весело.…Чтобы поглощать знания надо поглощать их с аппетитом”.

Повторим необходимые теоретические сведения в ходе разгадывания кроссворда.

По горизонтали:

1. Действие, с помощью которого вычисляется значение степени (возведение).

2. Произведение, состоящее из одинаковых множителей (степень).

3. Действие показателей степеней при возведении степени в степень (произведение).

4. Действие степеней, при которых показатели степеней вычитаются (деление).

По вертикали:

5. Число всех одинаковых множителей (показатель).

6. Степень с нулевым показателем (единица).

7. Повторяющийся множитель (основание).

8. Значение 10 5: (2 3 5 5) (четыре).

9. Показатель степени, который обычно не пишут (единица).

IV
. Математическая разминка.

Учитель.
Повторим определение степени с рациональным показателем и его свойства, выполним следующие задания.

1. Представить выражение х 22 в виде произведения двух степеней с основанием х, если один из множителей равен: х 2 , х 5,5 , х 1\3 , х 17,5 , х 0

2. Упростить:

б) у 5\8 у 1\4: у 1\8 = у

в) с 1,4 с -0,3 с 2,9

3. Вычислить и составить слово, используя дешифратор.

Выполнив это задание, вы, ребята, узнаете фамилию немецкого математика, который ввел термин — “показатель степени”.

1) (-8) 1\3 2) 81 1\2 3) (3\5) -1 4) (5\7) 0 5) 27 -1\3 6) (2\3) -2 7) 16 1\2 * 125 1\3

Слово:

1234567 (Штифель)

Определение и основные свойства степени с целым показателем

Для любого действительного числа

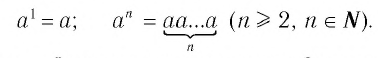
Для любого действительного числа полагаем

Свойства действий над степенями с целыми показателями

Свойства действий над степенями с целыми показателями сформулированы в следующей теореме.

Теорема 1.

Для любых значений и при любых целых и верны равенства:

Сформулируем также теорему о возведении в степень обеих частей неравенства.

Теорема 2.

Пусть и — неотрицательные числа, — натуральное число. Тогда:

1. если то
2. если то

Доказательство:

Проведем доказательство методом от противного.

Допустим, что неравенство неверное. Тогда верно одно из двух соотношений: или .

Если , то . Это противоречит условию.

Если , то согласно первой части этой теоремы . Опять получили противоречие с условием.

Значит,

Пример №1

Сравнить числа и 9.

Решение:

Поскольку и верно неравенство , т. е. , то по теореме 2 будет верным и неравенство , т. е. .

Ответ: .

Пример №2

Известно, что . Верно ли неравенство ?

Решение:

Если , то из верного неравенства следует, что верно и неравенство .

Если , то гарантировать, что, когда верно неравенство , будет верным и неравенство , нельзя. Например, неравенство верное, а неравенство неверное.

Следствие:

Пусть и — числа одного знака, — натуральное число. Тогда, если , то .

Доказательство:

Проведем его методом от противного. Допустим, что , например .

Если и — положительные числа, то согласно теореме 2 верно неравенство . Получили противоречие с условием. Значит, . Если и — отрицательные числа, то и — положительные числа, и если , то, как только что было доказано, , а значит,

И Заметим, что при использовании этого следствия необходимо проверять совпадение знаков и при четном , а при нечетном такой необходимости нет.

Заказать решение задач по высшей математике

Пример №3

Верно ли, что , если:

а) ; б)?

Решение:

а) Верно, если и — числа одного знака, и неверно, если они разных знаков. Например, — верное числовое равенство, но равенство — неверное.

б) Поскольку число и его нечетная степень всегда имеют один и тот же знак, то из того, что — верное числовое равенство, следует равенство чисел и .

Пример №4

Выполнить действия:

а) ; б) .

Решение:

а ).

б) .

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Корень n-й степени
• Тождества с корнями, содержащие одну переменную
• Действия с корнями нечетной степени
• Действия с корнями четной степени
• Показательно-степенные уравнения и неравенства
• Показательные уравнения и неравенства
• Логарифмические уравнения и неравенства
• Степенная функция — определение и вычисление

Степени с рациональными показателями

Степени с действительными показателями. Будем, как и в п. 11, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда m делится нацело на n,

Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:

В случае отрицательного рационального показателя степени —p/q полагают (по аналогии со случаем целого отрицательного показателя степени)

На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 11 действий над корнями. Докажем, например, свойство

Имеем

Так же получим Отсюда

что и требовалось доказать.

Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения при иррациональном х кладется последовательное приближение х рациональными числами. Так, например, для следует рассмотреть приближения по недостатку и по избытку для и возводить 3 в соответствующие рациональные степени, записывая

По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься за десятичные знаки, определяющие иррациональное число . Более подробно рассматривать этот вопрос мы не можем, но отметим, что имеет действительное вполне определенное значение при а > 0 и любом действительном х.

Замечание:

Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению при а < 0 также можно приписать смысл с помощью равенства в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.

Пример:

Произвести действия, пользуясь отрицательными и дробными показателями степени: .

Решение:

Свойства степени с целым показателем

Правила действий со степенями, имеющими целый показатель, не отличаются от тех, которые мы . Напомним их.

Убедимся в этом на нескольких примерах:

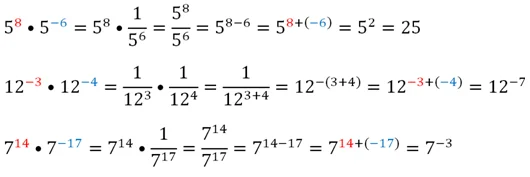
Однако эти примеры ещё не являются полноценными доказательствами этого свойства степеней. Приведем общее доказательство для того случая, когда число в натуральной степени умножается на число в отрицательной степени:

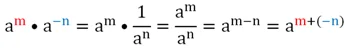
Также докажем справедливость этого правила и в том случае, когда перемножаются два числа в отрицательной степени:

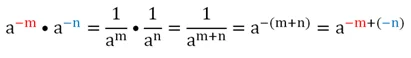
Проиллюстрируем это:

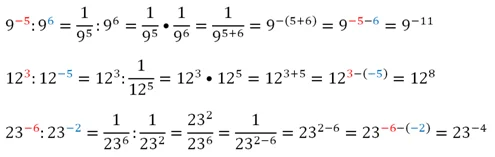
Для строгого доказательства заменим операцию деления на умножение. Так как

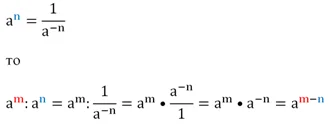
Здесь мы сначала заменяем степень an на дробь 1/а– n (по определению отрицательной степени), а потом пользуемся тем, что равносильно умножению на «перевернутую дробь».

Продемонстрируем применение этого правила:

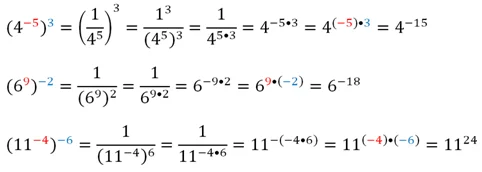
Следующие правила позволяют работать со степенями, у которых различаются основания, но совпадают показатели:

Покажем, как это работает:

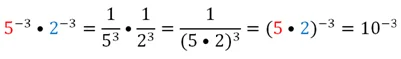
Для общего случая доказательство будет выглядеть так:

Это правило можно проиллюстрировать так:

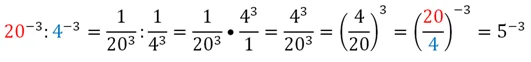
Приведем доказательство этого свойства для отрицательных степеней с целым показателем:

Как видим, свойства степеней с целыми показателями (в частности, с отрицательными), не отличаются от уже изученных нами свойств степеней с натуральными показателями. Единственное исключение – добавляется дополнительное ограничение, согласно которому основанием степени с отрицательным целым показателем не может быть ноль. То есть запись 0– 3 не имеет смысла, хотя выражение 03 имеет смысл:

03 = 0•0•0 = 0

Тождественные преобразования

Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.

Например, чтобы представить выражение 2−1 × 2−3 в виде степени, можно воспользоваться основным свойством степени:

2−1 × 2−3 = 2−1 + (−3) = 2−4

Пример 2. Найти значение выражения 5−15 × 516

Воспользуемся основным свойством степени:

5−15 × 516 = 5−15 + 16 = 51 = 5

или:

Видим, что первый вариант решения намного проще и удобнее.

Пример 3. Найти значение выражения (10−4)−1

Воспользуемся правилом возведения степени в степень:

(10−4)−1 = 10−4 × (−1) = 104 = 10000

Пример 4. Найти значение выражения 

Представим число основание 10 в виде произведения 2 × 5. Тогда числитель примет вид (2 × 5)−6

В числителе применим правило возведения в степень произведения:

Сократим получившуюся дробь на 5−6

Вычислим степень 2−6

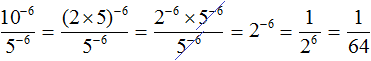
Основные виды преобразований степенных выражений

Со степенными выражениями можно выполнять любые из основных тождественных преобразований выражений . Например, можно раскрывать скобки, заменять числовые выражения их значениями, приводить подобные слагаемые и т.д. Естественно, при этом стоит надо соблюдать принятый порядок выполнения действий . Приведем примеры.

Пример.

Вычислите значение степенного выражения 2 3 ·(4 2 −12)
.

Решение.

Согласно порядку выполнения действий сначала выполняем действия в скобках. Там, во-первых, заменяем степень 4 2
ее значением 16
(при необходимости смотрите ), и во-вторых, вычисляем разность 16−12=4
. Имеем 2 3 ·(4 2 −12)=2 3 ·(16−12)=2 3 ·4
.

В полученном выражении заменяем степень 2 3
ее значением 8
, после чего вычисляем произведение 8·4=32
. Это и есть искомое значение.

Итак, 2 3 ·(4 2 −12)=2 3 ·(16−12)=2 3 ·4=8·4=32
.

Ответ:

2 3 ·(4 2 −12)=32
.

Пример.

Упростить выражения со степенями 3·a 4 ·b −7 −1+2·a 4 ·b −7
.

Решение.

Очевидно, что данное выражение содержит подобные слагаемые 3·a 4 ·b −7
и 2·a 4 ·b −7
, и мы можем привести их: .

Ответ:

3·a 4 ·b −7 −1+2·a 4 ·b −7 =5·a 4 ·b −7 −1
.

Пример.

Представьте выражение со степенями в виде произведения.

Решение.

Справиться с поставленной задачей позволяет представление числа 9
в виде степени 3 2
и последующее использование формулы сокращенного умножения разность квадратов:

Ответ:

Также существует ряд тождественных преобразований, присущих именно степенным выражениям. Дальше мы их и разберем.

Что такое степенные выражения?

Термин «степенные выражения» практически не встречается школьных учебниках математики, но он довольно часто фигурирует в сборниках задач, особенно предназначенных для подготовки к ЕГЭ и ОГЭ, например, . После анализа заданий, в которых требуется выполнить какие-либо действия со степенными выражениями, становится понятно, что под степенными выражениями понимают выражения, содержащие в своих записях степени. Поэтому, для себя можно принять такое определение:

Определение.

Степенные выражения
– это выражения, содержащие степени.

Приведем примеры степенных выражений
. Причем будем их представлять согласно тому, как происходит развитие взглядов на от степени с натуральным показателем до степени с действительным показателем.

Как известно, сначала происходит знакомство со степенью числа с натуральным показателем, на этом этапе появляются первые самые простые степенные выражения типа 3 2
, 7 5 +1
, (2+1) 5
, (−0,1) 4
, 3·a 2 −a+a 2
, x 3−1
, (a 2) 3
и т.п.

Чуть позже изучается степень числа с целым показателем, что приводит к появлению степенных выражений с целыми отрицательными степенями, наподобие следующих: 3 −2
, , a −2 +2·b −3 +c 2
.

В старших классах вновь возвращаются к степеням. Там вводится степень с рациональным показателем, что влечет появление соответствующих степенных выражений: , , и т.п. Наконец, рассматриваются степени с иррациональными показателями и содержащие их выражения: , .

Перечисленными степенными выражениями дело не ограничивается: дальше в показатель степени проникает переменная, и возникают, например, такие выражения 2 x 2 +1
или . А после знакомства с , начинают встречаться выражения со степенями и логарифмами, к примеру, x 2·lgx −5·x lgx
.

Итак, мы разобрались с вопросом, что представляют собой степенные выражения. Дальше будем учиться преобразовывать их.

Свойство степени с рациональным показателем

От целых показателей степени числа z мы переходим к рациональным показателем степеням. Далее мы определим степень с рациональным показателем, причем будем производить расчеты так, чтобы сохранялись все свойства степени с целым показателем. Это обязательно, потому что целые числа являются непосредственно частью рациональных чисел.

Свойство степени с рациональным показателем значительно облегчает изучение степеней в целом. Изучив данный метод, можно легко научится решать задачи различного уровня сложности. 

Рассмотрим основные свойства степени с рациональным показателем.

а) Произведение степеней с основаниями, которые имеют одинаковые значения.

 б) Свойство частного значения.

\

Доказательство данного свойства идентично по сравнению с предыдущим.

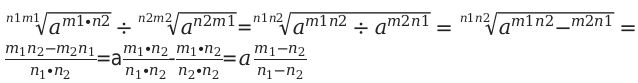
в) Свойство произведения в степень в виде дроби

\

г) Свойство степени в степени.

д) Свойство сравнения степеней со значениями равными между собой

zm<ym — условие любых положительных значений z и y, z < y и любом рациональном значении m>0.

Отсюда следует неравенство: m<0·zm>ym

е) Условие рациональных чисел

zx<zy, при следующем условии:

x > y   при 0<z<1; если z>0 zx>zy

 Для того чтобы доказать все перечисленные  условия, нам необходимо будет вспомнить, понятие степени с дробным показателем. 

Рассмотрим  свойство с рациональным показателем на примере:

Пример №1.

\

Пример № 2: необходимо вычислить \

Преобразуя уравнение, мы получим следующий вид: 415=(43)5далее записываем в виде \{\left(4^{3}\right)^{5}}=4^{3}=64\]

Преобразование выражений с корнями и степенями

Часто в выражениях, в которыми требуется провести некоторые преобразования, вместе со степенями с дробными показателями присутствуют и корни. Чтобы преобразовать подобное выражение к нужному виду, в большинстве случаев достаточно перейти только к корням или только к степеням. Но поскольку работать со степенями удобнее, обычно переходят от корней к степеням. Однако, осуществлять такой переход целесообразно тогда, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков (это мы подробно разобрали в статье переход от корней к степеням и обратно
После знакомства со степенью с рациональным показателем вводится степень с иррациональным показателем, что позволяет говорить и о степени с произвольным действительным показателем. На этом этапе в школе начинает изучаться показательная функция
, которая аналитически задается степенью, в основании которой находится число, а в показателе – переменная. Так мы сталкиваемся со степенными выражениями, содержащими числа в основании степени, а в показателе — выражения с переменными, и естественно возникает необходимость выполнения преобразований таких выражений.

Следует сказать, что преобразование выражений указанного вида обычно приходится выполнять при решении показательных уравнений
и показательных неравенств
, и эти преобразования довольно просты. В подавляющем числе случаев они базируются на свойствах степени и нацелены по большей части на то, чтобы в дальнейшем ввести новую переменную. Продемонстрировать их нам позволит уравнение 5 2·x+1 −3·5 x ·7 x −14·7 2·x−1 =0
.

Во-первых, степени, в показателях которых находится сумма некоторой переменной (или выражения с переменными) и числа, заменяются произведениями. Это относится к первому и последнему слагаемым выражения из левой части:5 2·x ·5 1 −3·5 x ·7 x −14·7 2·x ·7 −1 =0
,5·5 2·x −3·5 x ·7 x −2·7 2·x =0
.

Дальше выполняется деление обеих частей равенства на выражение 7 2·x
, которое на ОДЗ переменной x
для исходного уравнения принимает только положительные значения (это стандартный прием решения уравнений такого вида, речь сейчас не о нем, так что сосредоточьте внимание на последующих преобразованиях выражений со степенями):

Теперь сокращаются дроби со степенями, что дает .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению , которое равносильно . Проделанные преобразования позволяют ввести новую переменную , что сводит решение исходного показательного уравнения к решению квадратного уравнения

И. В. Бойков, Л. Д. Романова
Сборник задач для подготовки к ЕГЭ. Ч. 1. Пенза 2003.

Степени правила действия со степенями

1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):

(abc…) n = a n b n c n …

Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = 3 =(x +a) 3 (x — a) 3

Практически более важно обратное преобразование:

a n b n c n … = (abc…) n

т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.

Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 = 2 =(a 3 +b 3) 2

2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:

Пример 5. Пример 6.

Обратное преобразование:. Пример 7.. Пример 8..

3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:

Пример 9.2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .

4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого

Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.

5. При возведении степени в степень показатели степеней перемножаются:

Пример 13. (2 3) 2 =2 6 =64. Пример 14.

www.maths.yfa1.ru