Цилиндр, конус, шар

Виды конусов

1. Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания.
2. Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
3. Усеченный конус (конический слой) – часть конуса, которая остается между его основанием и секущей плоскостью, параллельной данному основанию.
4. Круговой конус – основанием фигуры является круг. Также бывают: эллиптический, параболический и гиперболический конусы.
5. Равносторонний конус – прямой конус, образующая которого равняется диаметру его основания.

Формула площади конуса

Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:

S = Sбок.пов + Sосн = πRL + πR2

Источники

• https://studwork.org/spravochnik/matematika/obemy-figur/obem-konusa
• https://calcsbox.com/post/formula-obema-konusa.html
• https://worksbase.ru/matematika/formuly/37-konus.html
• https://ru.onlinemschool.com/math/formula/volume/
• https://allcalc.ru/node/36
• https://ru.onlinemschool.com/math/formula/cone/
• https://www.calc.ru/1430.html
• https://MicroExcel.ru/obyom-konusa/
• https://www.calc.ru/obyem-konusa.html
• https://mnogoformul.ru/obem-konusa-formula-i-raschet-onlayn

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

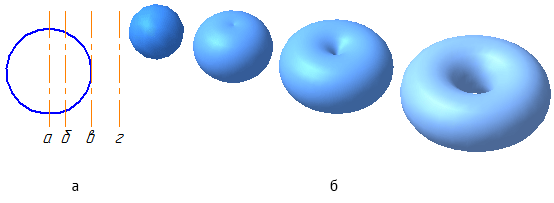
Рисунок 7.4 – Образование поверхностей вращения

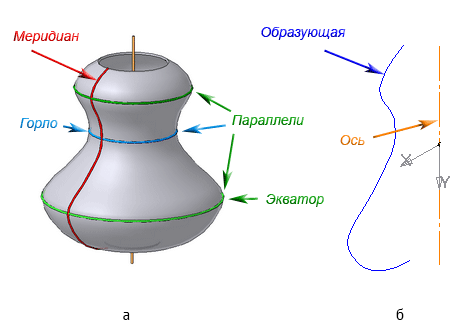
Рисунок 7.5 – Элементы поверхности вращения

Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).

Наименьшая параллель называется горлом, наибольшая – экватором.

Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.

Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.

Конус

Определение 2

Конусом называется тело, образованное вращением прямоугольного треугольника вокруг его катета.

Если прямоугольный треугольник $OPA$ вращать вокруг катета $PO$, его гипотенуза $PA$ опишет боковую поверхность, а катет $OA$ — круг — основание конуса (рис.6). Радиус этого круга называют радиусом конуса, точку $P$, отрезок $PO$, прямую $PO$ — соответственно вершиной, высотой и осью конуса. Все осевые сечения конуса — равные равнобедренные треугольники. Каждая плоскость, проходящая через ось конуса, является плоскостью его симметрии. Центра симметрии конус не имеет.

Рисунок 6.

Отрезок, соединяющий вершину конуса с любой точкой окружности его основания, — образующая конуса. Все образующие конуса равны, поскольку каждая из них равна гипотенузе треугольника, вращением которого образован конус. Плоскость, проходящая через образующую конуса и не имеющая с ним других общих точек, называется касательной плоскостью к конусу. Она перпендикулярна к осевому сечению, проведенному через эту же образующую (рис. 7).

Рисунок 7.

Рисование шара

Геометрическая форма шара самая простая из всех фигур, но для рисунка шар является самым сложным заданием. В первую очередь, начинающим сложно нарисовать ровный круг, трудно добиться плавных тональных переходов при штриховке, чтобы шар на рисунке не имел вмятин. Шар можно осветить естественным светом от окна или мягким светом с рассеивателем. Такой свет лучше, он не даёт резких теней.

При освещении лампой накаливания контраст сильнее, часто это приводит к тому, что начинающие изображают шар слишком тёмным, как будто он не из гипса, а из свинца.

Ниже представлен готовый рисунок шара. Изображения поэтапного ведения работы, построения теней, объяснения природы рефлексов появятся на сайте позже.

После того, как освоен рисунок геометрических тел по отдельности, можно приступить к рисованию группы из геометрических тел. Как правило, композиция включает в себя куб или параллелепипед, 1-2 тела вращения и шар. Рисунок кувшина также выполняется после того, как ученик умеет изображать простые геометрические формы.

Разрешено копирование статей, только при наличии активной (кликабельной) ссылки на страницу-источник сайта Дениса Гаврилова gavrilovart.ru и при указании авторства. Ссылка должна находиться непосредственно рядом с материалом, должна быть видимой и прямой (без использования java-скриптов).Запрещено каким-либо образом изменять, затирать, отрезать копирайты на копируемых с моего сайта фотографиях или иллюстрациях.

Основные элементы конуса

• R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
• h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
• Точка C – вершина конуса.
• l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
• Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
• Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

l2 = h2 + R2

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

• длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
• α – угол развёртки (или центральный угол);
• l – радиус сектора.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.

Упражнение

Заданы: сфера и  прямая общего положения АВ.

Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).

Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:

1. Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
2. Построить фигуру пересечения сферы вспомогательной плоскостью;
3. Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).

Решение

Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:

Рисунок 7.12 – Пересечение прямой с поверхностью сферы

• Введём π₃⊥π₁ и π₃//σ₁. Построим проекцию окружности сечения на π₃ и проекцию А₃В₃.
• Находим точки их пересечения 1₂ и 2₃.
• Определим видимость участков прямой.
• На π₁ точки 1 и 2 находятся на переднем полушарии, следовательно, на π₂ они видимы.

Рисунок конуса

Конус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. В нашем случае конус прямой, его ось перпендикулярна основанию.

При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа. Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.

Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания. Определив таким образом высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса.

Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.

Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми.

Следующий этап – построение эллипса

При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина. Чтобы передать объём в линии, ближнюю часть овала сделаем темнее

После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба. Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее.

Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.

Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали

Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму. Освещённая часть чуть темнее снизу, сверху выше контраст света и тени

Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы

Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы.

Размеры и допуски углов наружных и внутренних конусов

* Размер для справок.

** Z — базорасстояние конуса задает­ся в стандартах на конкретную про­дукцию

1 — основная плоскость; 2 — базовая плоскость

Обозначенияконусов	D	d	Lрасч	Допуск угла, мкм, конуса ATDпо ГОСТ 8908
3	4	5	6	7
30	31,75	17,750	48	2,5	4	6	10	15
35	38,10	21,767	56	2,5	4	6	10	15
40	44,45	25,492	65	3,0	5	8	12	20
45	57,15	32,942	83	3,0	5	8	12	20
50	69,85	40,100	102	4,0	6	10	16	25
55	88,90	54,858	127	4,0	6	10	16	25
60	107,95	60,700	162	5,0	8	12	20	30
65	133,35	74,433	202	5,0	8	12	20	30
70	165,10	92,183	250	6,0	10	16	25	40
75	203,20	113,658	307	6,0	10	16	25	40
80	254,00	138,208	394	8,0	12	20	30	50

Условное обозначение конусов по ГОСТ 15945 с добавлением степени точности конуса:

Конус 50 АТ5 ГОСТ 15945-82

Предельные отклонения базорасстояния конуса Z следует выбирать из ряда: ± 0,4; ± 0,2; ± 0,1; ± 0,05мм.

Продолжение табл. 10

7.8. Коническая поверхность

Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).

Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом.

Плоская фигура, ограниченная конической поверхностью, называется основанием конуса.

Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса.

Если основание конуса является кругом, то конус называется круговым.

Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым.

Перемещая точку A» — можно изменять диаметр основания конуса;
перемещая точку O’ — можно менять положение точки на поверхности конуса.

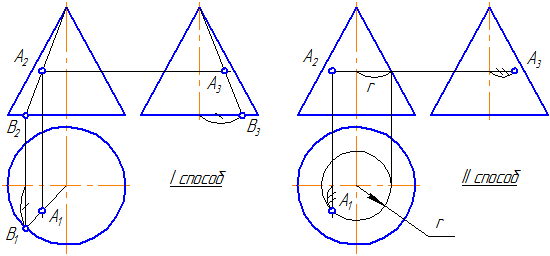
Рисунок 7.13 – Принадлежность точки конической поверхности

Рассмотрим вопрос принадлежности точки А поверхности конуса.Дана фронтальная проекция точки А и она видима (Рисунок 7.13).

1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса,  построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.

2 способ. Точка А лежит на параллели конуса радиусом r. На π₁ строим проекцию окружности (параллели) и по линии проекционной связи находим А₁. По двум проекциям точки строим третью.

Развёртка

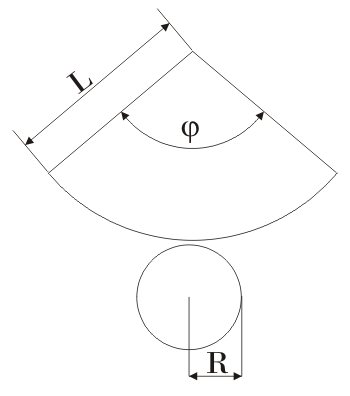
Развёртка прямого кругового конуса Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h

— высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольникаr — радиус в основании конуса. Гипотенузой прямоугольного треугольника являетсяl — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r

иl . Радиус основанияr определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхностиl , являющаяся радиусом сектора боковой поверхности. Угол сектора φ {\displaystyle \varphi } в развёртке боковой поверхности конуса определяется по формуле: φ = 360°·(r /l ).

Публикация «Конспект НОД по математике во второй младшей группе „Цилиндр, конус“» размещена в разделах

• Конспекты занятий. Все конспекты
• Математика. Конспекты занятий по ФЭМП
• Математика. Математические представления, ФЭМП
• Цилиндр. Все о цилиндрах для детей
• Темочки
• Конкурс для воспитателей и педагогов «Лучший конспект занятия (НОД)» февраль 2016

Материалы и оборудование: цилиндр и конус; картинки с изображением предметов цилиндрической и конусовидной форм; кукла Зима; заготовки из бумаги: для изготовления фонарика на основе цилиндра и осьминожка на основе конуса; клей.

Ход НОД

Воспитатель здоровается с детьми:

-Здравствуйте, ладошки! Хлоп, хлоп, хлоп! Здравствуйте, ножки! Топ, топ, топ!

Здравствуйте, щечки! Плюх, плюх, плюх! Пухленькие щечки, плюх, плюх, плюх!

Здравствуйте, губки! Чмок, чмок, чмок! Здравствуйте, зубки, щелк, щелк, щелк!

Здравствуй, носик, пип, пип, пип! Здравствуйте, детки, всем привет!

Дети выполняют движения в соответствии с текстом.

Воспитатель. -Дети, вы сказки любите? Какие? Сегодня я хочу рассказать и показать вам одну сказку. Жили-были в городе Математики Цилиндр и Конус. Вот и они, пришли к вам в гости.

-Как вы думаете, кто из них Цилиндр, а кто Конус? Я вам подскажу: Цилиндр больше Конуса. Давайте рассмотрим, как он выглядит. (рассматривают, отмечают цвет, как выглядит с разных сторон. ) Какого цвета Конус? Как он выглядит сверху? А на что похож сбоку? Чем отличаются между собой Цилиндр и Конус?

-Наши новые знакомые все время спорили, кто из них главнее и лучше. Цилиндр говорил, что без него не бывает кастрюль, а значит, завтрака, обеда и ужина, что очень много вкусных вещей спрятаны в баночки цилиндрической формы. Это сгущенка, зеленый горошек, консервированные овощи и фрукты. (На доске вывешиваются соответствующие картинки. ) Конус утверждал, что он намного лучше и красивее, ведь на него похожи вкусное мороженое, полезная морковка, а самое главное, елочка. (Вывешиваются картинки. ) Так Цилиндр и Конус сначала спорили, потом ссорились, а потом и вовсе перестали разговаривать и дружить. Дети, а разве хорошо ссориться? Что вы можете предложить нашим гостям? Давайте скажем Цилиндру и Конусу, чтобы они помирились, ведь, если они будут дружить, мы сможем построить из них чудесную башенку. (Дети предлагают формам помириться. ) Давайте развеселим их веселой песенкой-считалочкой.

Физминутка «Считалочка» (дети танцуют под развивающую песенку «Считалочка»)

Воспитатель. -Дети, посмотрите, Цилиндр и Конус так весело танцевали и прыгали, что из них получилась башенка. Кто из них стоит внизу? А кто вверху? Дети, Цилиндр и Конус очень рады, что вы их помирили. Пора им возвращаться в свою сказку, но они часто будут приходить к вам. Скажите им: «До свидания!»

Воспитатель. — Ой, к нам кто-то стучится. Кто же это может быть? (Появляется кукла в серебристой одежде. ) -Дети, да это же сама Зима пришла к нам в гости. Поздоровайтесь с ней. (Дети здороваются)

Воспитатель. -Здравствуй, гостья-зима,

Просим милости к нам,

Песни севера петь

По лесам и степям.

Зима. -Здравствуйте, ребята. С кем вы сегодня познакомились? (Ответы детей. ) Я очень рада, что вы их помирили, и принесла для вас цилиндр и конус из бумаги. Из них можно сделать красивые игрушки для новогодней елочки.

Воспитатель с помощью детей делает из заготовок фонарик и осьминога.

Зима: -Замечательные игрушки! Я думаю, они понравятся елочке. А я останусь у вас на целых 3 месяца, чтобы играть с вами, встречать новый год, петь песенки, кататься на санках и лепить снеговиков.

Поверхность и ось вращения

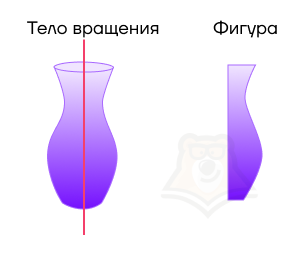
На примере выше мы видим вазу. Она состоит только из “оболочки” и полая внутри. В математике существует название и для этой оболочки. Называется она поверхностью вращения. 

Поверхность вращения — граница тела вращения. 

Иными словами, поверхность вращения является внешней оболочкой тела вращения и ограничивает его в пространстве. Как кожа у человека. 

Ось, вокруг которой мы вращаем фигуру, называется осью вращения. 

Ось вращения может по-разному располагаться относительно фигуры. 

Ось совпадает с одной из ее сторон. 

Выше мы уже рассмотрели пример цилиндра и вазы. В их случае ось вращения лежит на одной из сторон фигуры, которую мы вращаем. 

Ось лежит внутри фигуры. 

Например, ось может проходить через центр фигуры. Попробуем прокрутить  овал вокруг его горизонтальной оси, проходящей через центр.

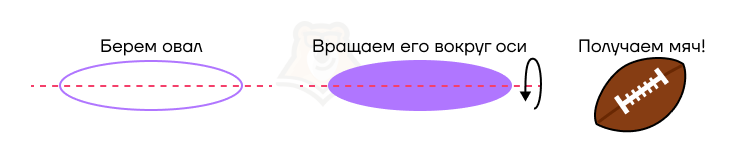
Мы получим эллипсоид. Эта фигура очень похожа на мяч для американского футбола.

Ось лежит вне фигуры. 

Например, если мы будем вращать круг относительно оси, лежащей за его пределами, то получим “кольцо”.

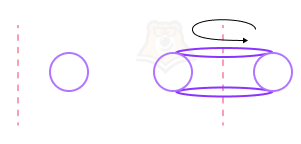
Такая фигура в математике называется тором. 

Причем тут тор и почему он без Локи?Разумеется, когда в математике упоминается тор, имеет в виду не скандинавский бог. Тор — тело вращения, которое получается при вращении круга вокруг оси, лежащей за его пределами.

Среди тел вращения в математике наиболее часто встречаются цилиндр, конус, шар, эллипсоид и тор. Подробнее про некоторые из них можно прочесть в статьях «Цилиндр», «Конус», «Шар». 

Слайды и текст этой презентации

сечении конуса плоскостью,проходящей через ось конуса?Какая фигура получается в сечении

конуса плоскостью,проходящей перпендикулярнооси конуса?

2

Какая фигура получается в сечении цилиндра плоскостью,проходящей перпендикулярнооси цилиндра?

Какая фигура получается в сечении цилиндра плоскостью,проходящей через ось цилинд-ра?

3

Что представляет собой сече-ние конуса плоскостью, прохо-дящей через вершину конуса?

Что представляет собой сечениеконуса плоскостью, параллель-ной двум образующим конуса?

4

Чему равна площадь осевогосечения конуса, если его высо-та в 2 раза больше радиуса ос-нования и равна 5 см?

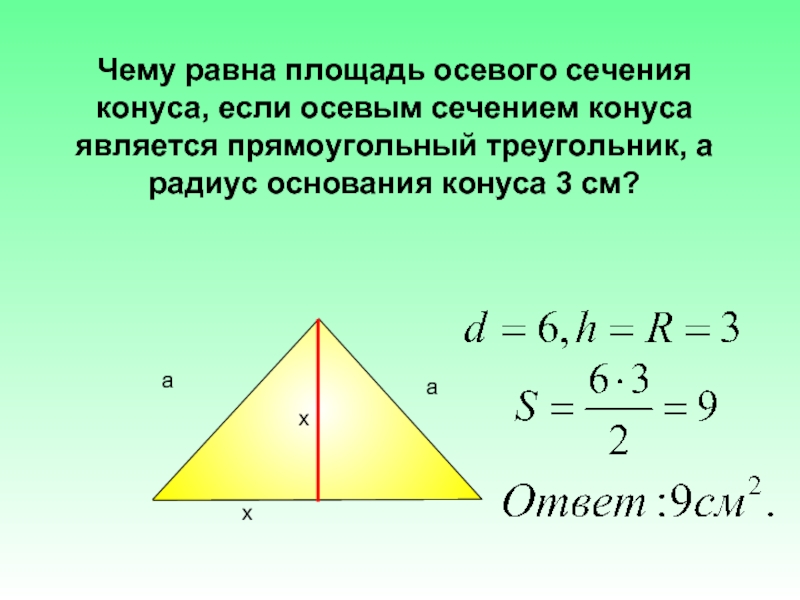
Чему равна площадь осевого се-чения конуса, если осевым сече-нием конуса является прямо-угольный треугольник, а радиус основания конуса 3 см?

5

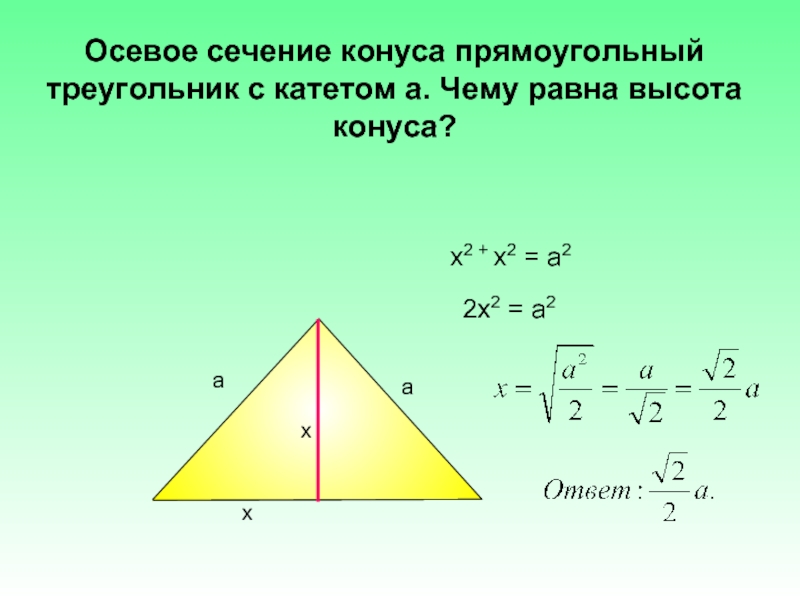
Осевое сечение конуса прямо-угольный треугольник с катетома. Чему равна высота конуса?

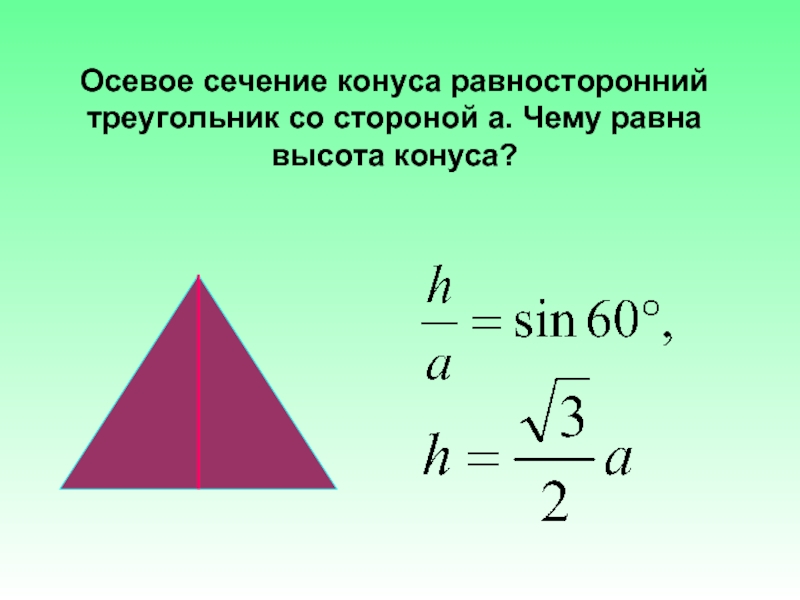
Осевое сечение конуса равносто-ронний треугольник со сторонойа. Чему равна высота конуса?

Слайд 4Какая фигура получается в
сечении конуса плоскостью,
проходящей через ось конуса?
Равнобедренный

Слайд 5Какая фигура получается в
сечении цилиндра плоскостью,
проходящей перпендикулярно
оси цилиндра?
Круг

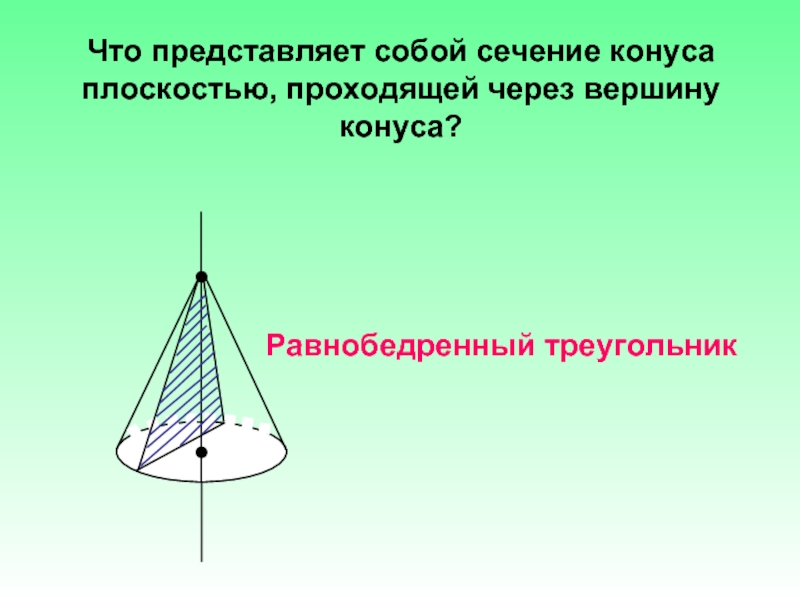
Слайд 6Что представляет собой сечение конуса плоскостью, проходящей через вершину конуса?
Равнобедренный

Слайд 9Какая фигура получается в
сечении конуса плоскостью,
проходящей перпендикулярно
оси конуса?
Круг

Слайд 10Какая фигура получается в
сечении цилиндра плоскостью,
проходящей через ось цилиндра?
Прямоугольник

Слайд 11Что представляет собой сечение конуса плоскостью,параллельной двум образующим конуса?
Гипербола

Онлайн-калькулятор

Общее определение конусаКонус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.

Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.

Рассмотрим некоторые важные понятия.

Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной. Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.

Конус бывает нескольких типов:

Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.

Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.

Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.

Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.

Цилиндр и конус

Цилиндром называется тело, которое состоит из 2 кругов,
совмещаемых параллельным переносом, и всех отрезков, сое-
диняющих соотв. точки этих кругов. Круги называются осно-
ванием цилиндра, а отрезки — образующими цилиндра. Также,
как и для призмы доказывается, что основания циллиндра
равны и лежат в параллельных плоскостях, образующие пара-
ллельны и равны.

Цилиндр называется прямым, если его образующие перпенди-
кулярны плоскостям оснований. Радиусом ц. называется рад-
иус его основания. Высота — расстояние между плоскостями
оснований. Ось — прямая, проходящая через центры основан.

Сечение ц. плоскостью, проходящей через ось ц. — осевое
сечение.

Теорема 19.1. Плоскость, перпендикулярная оси цилиндра,
пересекает его боковую поверхность по окружности, равной
окружности основания.

Докозательство. Пусть б — плоскость, перпендикулярная
оси цилиндра. Эта плоскость || основаиям. Параллельный
перенос в направлении оси ц., совмещающий плоскость б с
плоскостью основания ц., совмещает сечение б.п плоскостью
б с окружностью основания. Ч.Т.Д.

Призмой, вписанной в цилиндр, называется такая п., осно-
вания которой — равные многоугольники, вписанные в основа-
ние ц. Призма называется описанной около ц., если ее осно-
вания — равные многоугольники, описанные около основания
ц.

Конус
К. называется тело, которое состоит из круга — основания
к., точки не лежащей в плоскости этого круга, — вершины
конуса и всех отрезков, соединяющих вершину конуса с точ-
ками основания. Отрезки, соединяющие вершину к. с точками
окружности основания, называются образующими конуса. К.

называется прямым, если прямая соеденяющая вершину к. с
центром основания, перпендикулярна плоскости основания.

Высотой к. называется перпендикуляр, опущенный из его
вершины на плоскость основания. Осью прямого конуса назы-
вается прямая, содержащая его высоту. Сечение к. плос-
костью, проходящей через его ось, называется осевым сече-
нием. Плоскость, проходящая через образующую к. и перпен-
дикулярная осевому сечению, проведенному через эту обра-
зующую, называется касательной плоскостью конуса.

Теорема 19.2. Плоскость, перпендикулярная оси конуса,
пересекает конус по кругу, а боковую поверхность — по ок-
ружности, с центром на оси конуса.

Док-во. Пусть б — плоскость, перпендикулярная оси конуса
и пересекающая к. Преобразование гомотетии относительно
вершины к., совмещающее плоскость б с плоскостью основа-
ния, совмещает сечение к. плоскостью б с основанием к.

Следовательно, сечение к. плоскостью есть круг, а сечение
б.п. — окружность с центром на оси конуса.

Плоскость, перпендикулярная оси конуса, отсекает он него
меньший к. Оставшаяся часть называется усеченным к. Ч.Т.Д
Пирамидой, вписанной в конус, называется такая пирамида,
основание которой есть многоугольник, вписанный в окруж-
ность основания конуса, а вершиной является вершина кону-
са. Пирамида называется описанной около конуса, если ее
основанием является многоугольник, описанный около осно-
вания к., а вершина совпадает с вершиной к.

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

• прямая ОР – это ось конической поверх-ти;
• прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
• сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

• коническая поверх-ть конуса именуется его боковой поверх-тью;
• если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
• отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

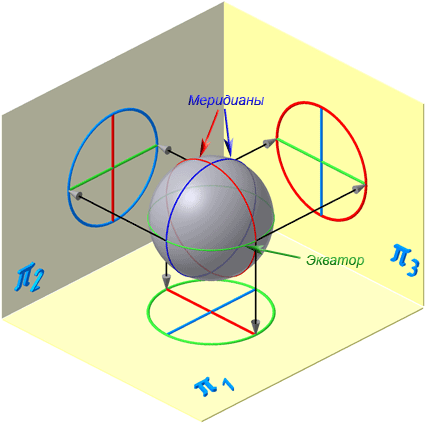Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.

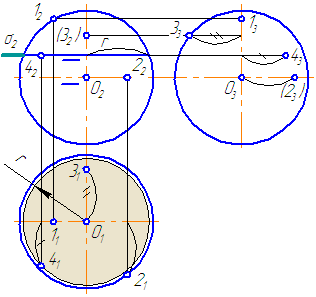Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

Связанные определения для конуса

Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.

Коническая поверхность. Образующая поверхность конуса является конической поверхностью.

Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.

Угол раствора конуса. Угол раствора конуса – угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).

Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.

Косой (наклонный) конус. Косой (наклонный) конус – конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.

Круговой конус. Круговой конус – конус, основание которого является кругом.

Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).

Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.

Объем конуса через радиус

Данный треугольник

для получения конуса должен вращаться вокруг одного из своихкатетов , который является не только осью вращения, но и высотой конуса.Второй же катет становится радиусом полученной в результате вращения окружности-основания конуса, а гипотенуза будет апофемой (высотой опущенной под прямым углом к линии окружности, а не центру).

Технически взаимосвязь конуса

с цилиндром идентична взаимосвязи пирамиды с кубом (параллелепипедом), единственное, что выводформулы проходит через отношения интегралов их сферических углов, но тем не менее, он точно также как и пирамида занимает одну треть цилиндра, в который он может быть вписан.

Поэтому его объем

равен произведению площади основания на высоту, деленному на три, или произведению числомπ на квадрат радиуса и высоту, деленному на три.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание!

Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно!

Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса

При этом важно, чтобы она была перпендикулярна осевому сечению

Слайд 2 Математический диктант Математический диктант11 вариант2 вариантКакая фигура получается в

сечении конуса плоскостью,проходящей через ось конуса?Какая фигура получается в сечении

конуса плоскостью,проходящей перпендикулярнооси конуса?

2

Какая фигура получается в сечении цилиндра плоскостью,проходящей перпендикулярнооси цилиндра?

Какая фигура получается в сечении цилиндра плоскостью,проходящей через ось цилинд-ра?

3

Что представляет собой сече-ние конуса плоскостью, прохо-дящей через вершину конуса?

Что представляет собой сечениеконуса плоскостью, параллель-ной двум образующим конуса?

4

Чему равна площадь осевогосечения конуса, если его высо-та в 2 раза больше радиуса ос-нования и равна 5 см?

Чему равна площадь осевого се-чения конуса, если осевым сече-нием конуса является прямо-угольный треугольник, а радиус основания конуса 3 см?

5

Осевое сечение конуса прямо-угольный треугольник с катетома. Чему равна высота конуса?

Осевое сечение конуса равносто-ронний треугольник со сторонойа. Чему равна высота конуса?