Производная и ее геометрический смысл

Геометрический смысл производной

Достроим прямоугольный треугольник АВС. Заметим, что отношение $\frac{\Delta x}{\Delta y} = tg(BAC)$, то есть равняется отношению противолежащего катета к прилежащему катету. Иначе это отношение можно записать как $tg(BAC) = \frac{BC}{AC}$.

Поскольку в этом примере мы взяли достаточно большое расстояние между значениями х, то АВ — секущая. Если мы будем сокращать расстояние между значениями аргумента, то две точки на графике будут ближе друг к другу, а секущая будет стремиться к касательной.

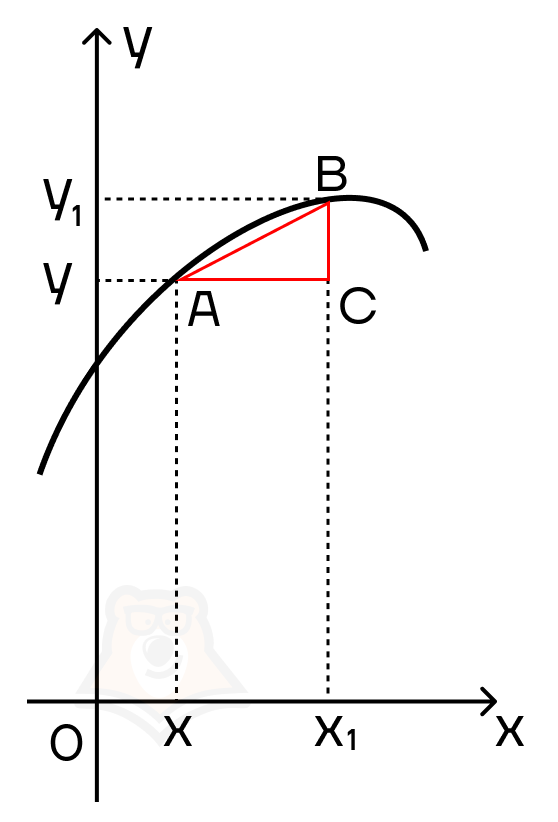
Следовательно, мы можем описать скорость изменения функции через тангенс угла наклона касательной, проведенной к графику функции в некоторой точке.

Из этих рассуждений мы можем вывести геометрический смысл производной:

Если провести касательную к функции в некоторой точке, то производная в этой точке будет равна тангенсу угла ее наклона.

Рассмотрим касательную отдельно. Это прямая, которая имеет уравнение y = kx+b, где к — коэффициент наклона.

Тогда мы получаем следующее уравнение:

f'(x) = k = tg(a)

Какие фокусы творят тригонометрия и геометрия вместе?Геометрический смысл производной — главный совместный номер. Производная равняется тангенсу угла наклона касательной, проведенной к функции в определенной точке.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.

Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.

Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
Схема Бернулли. Примеры решения задач
Комбинаторика в задаче B6: средний тест
Как решать задачи про летающие камни?
B4: счетчики на электричество

Геометрический смысл

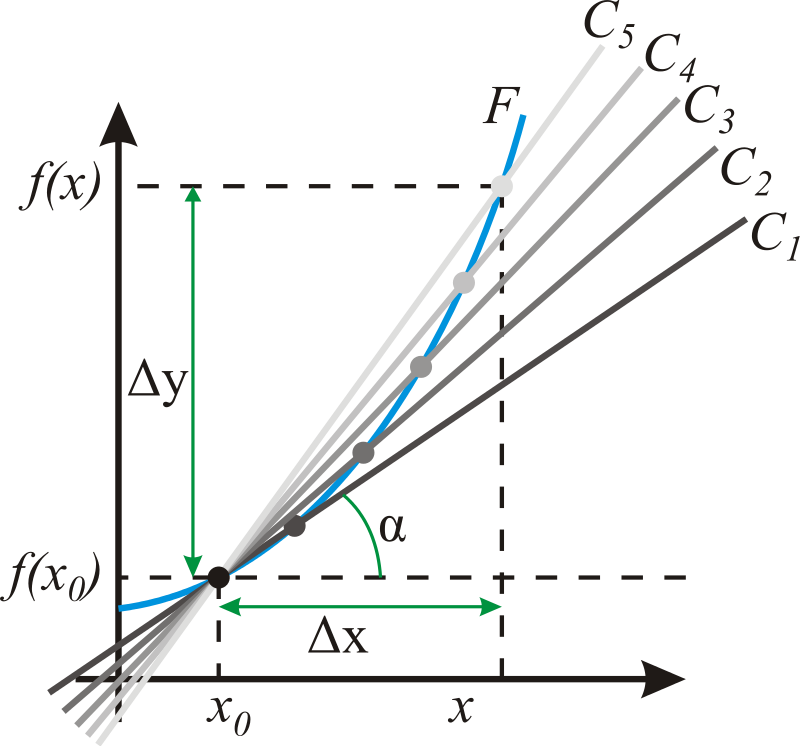
Производную можно объяснить с точки зрения геометрии. С этой целью потребуется изобразить график функции. Обозначим на нем абсциссу х0, а также определим ординату $f(х0)$, которая ей соответствует. На окрестности абсциссы поставим какую-то точку х и начертим секущую линию, пересекающую точки графического изображения функции F. На схеме эта линия отмечена как С5. Удаленность друг от друга точек х и х0 стремится к нулевому значению и обозначается в виде дельта х. Таким образом, можно наблюдать переход секущей в касательную через линии С5, С4, С3, С2, С1. В результате производная, характерна для точки х0, представляет собой тангенс угла $\alpha$.

Знак производной

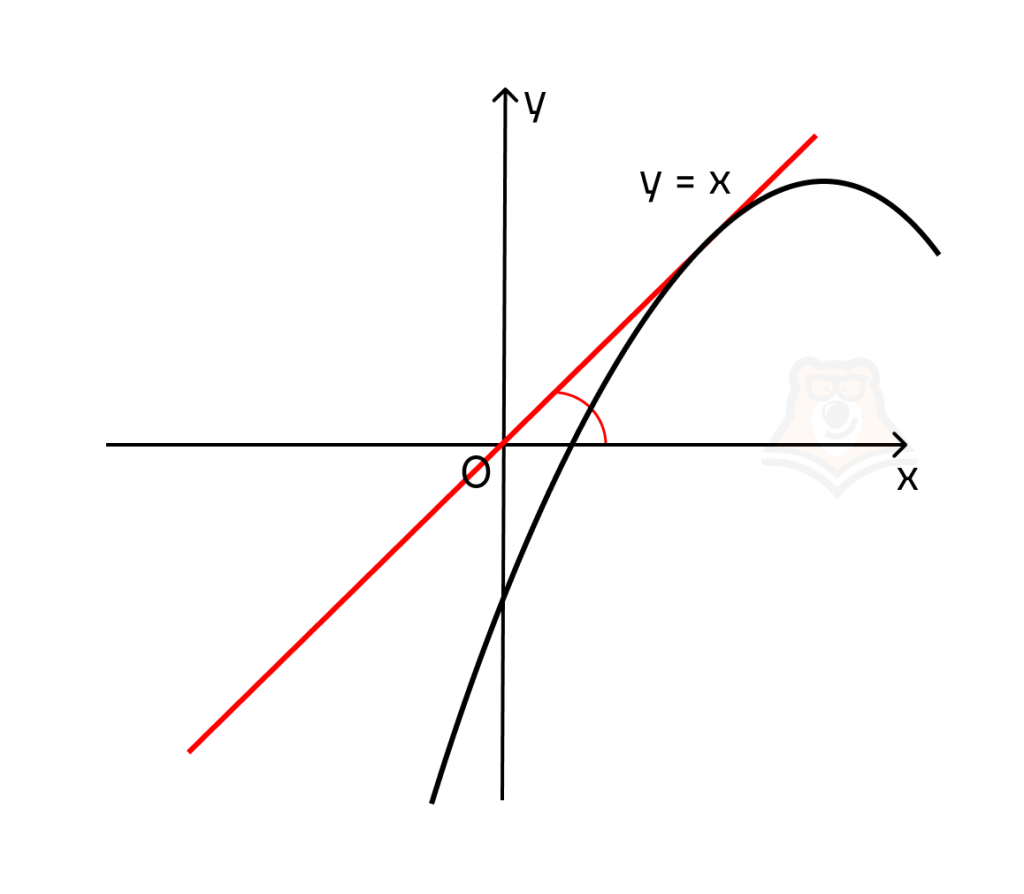
Построим графики двух прямых с разным углом наклона. Пусть в первом случае k = 1, а во втором k = -1. Тогда получаем графики функций у = х и у = -х.

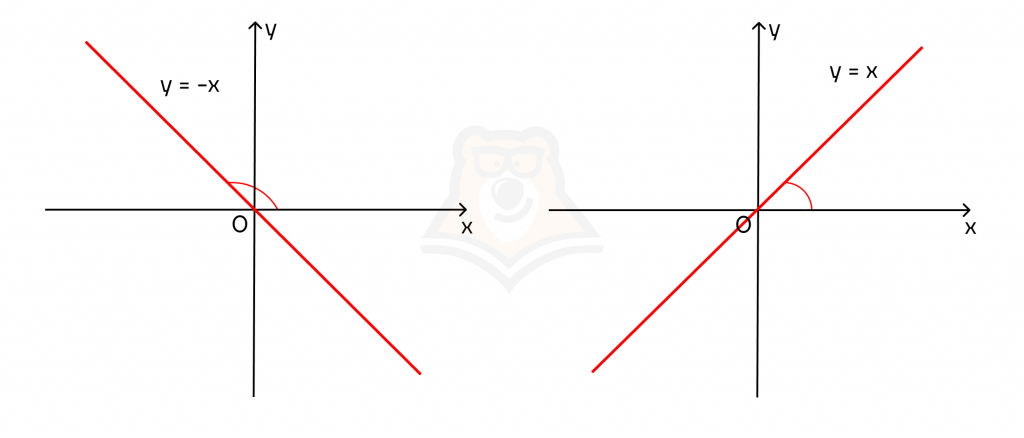
Заметим, что тангенс угла наклона имеет разные значения в этих случаях: tg(a) = -1 и tg(a) = 1.

Теперь достроим к касательным графики функций. В первом случае точка, к которой проведена касательная, будет лежать на участке функции, на котором она убывает. Во втором случае точка касания будет лежать на возрастающем участке функции.

Чтобы определить, убывает или возрастает функция, нужно посмотреть на ее наклон на участке.

Вспомним американские горки: пусть по функции будет слева направо ехать вагончик. В участках, где вагончик будет подниматься на гору, функция возрастает, а где вагончик съезжает с горки — функция убывает.

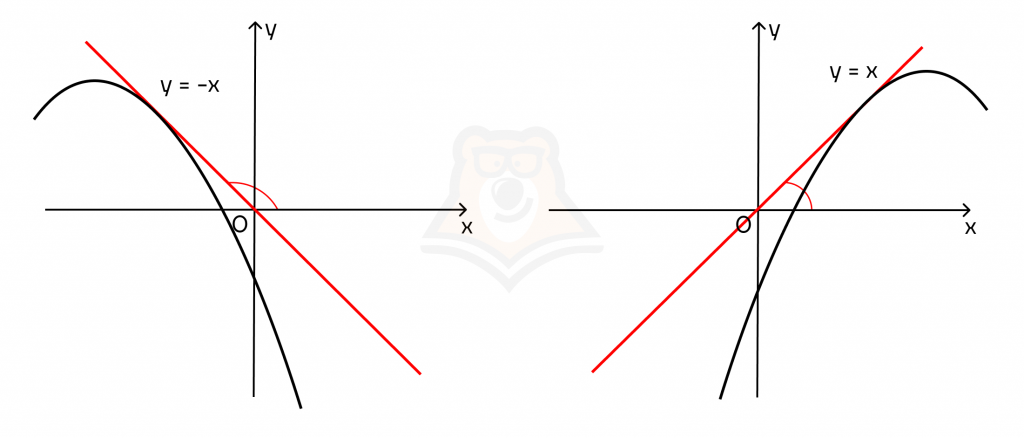
Из этих рассуждений мы можем вывести зависимость знака функции и знака производной.

1. Функция возрастает в точке тогда и только тогда, когда производная в данной точке положительна.

В этом случае касательная к функции также будет возрастать.

f'(x) = tg(a). Если tg(a) > 0, то и f'(x) > 0.

2. Функция убывает в точке тогда и только тогда, когда производная в данной точке отрицательна.

В этом случае касательная к функции будет убывать.

f'(x) = tg(a). Если tg(a) < 0, то и f'(x) < 0.

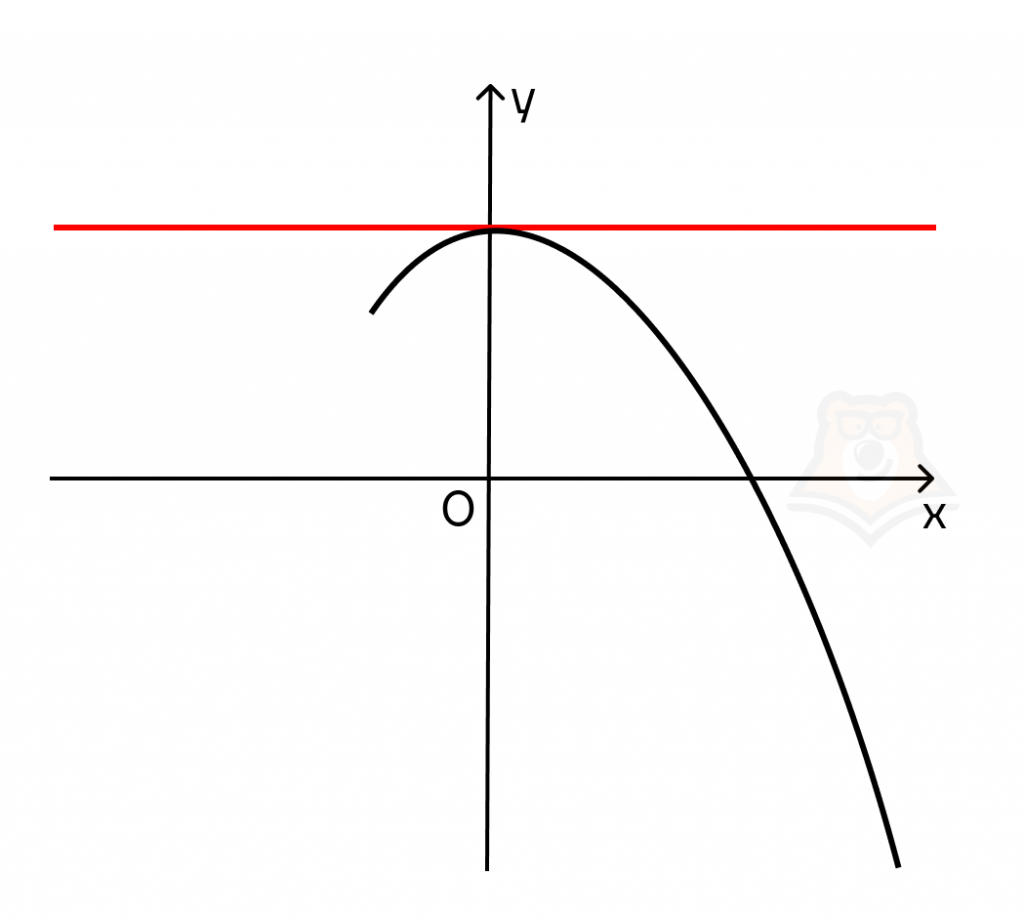
3. Если касательная к функции параллельна оси абсцисс, то производная в этой точке равна 0.

Поскольку прямая будет параллельна оси абсцисс, то у нее не будет угла наклона, а следовательно: k = tg(a) = 0 = f'(x).

Такие точки называются стационарными, это точки экстремума или седловые точки.

Подведем итог.Знак производной определяется по изначальной функции:

если функция возрастает, то производная положительна;
если функция убывает, то производная отрицательна;
в точках, где функция не возрастает и не убывает (стационарные точки), производная равна 0.

Определение производной

Предположим, что имеется некая функция y = f(x). Определим начальное значение и полученное значение x из области, в которой определена заданная функция. Проанализируем эти значения.

Заметим, что в данном случае обозначение является единым и не определяется, как произведение, то есть:

Записанная ранее функция принимает в начальной точке значение, равное . Если задать аргументу x приращение , то результатом станет значение функции в другой точке .

Условием наличия у функции y = f(x) производной на некотором интервале (a;b) является существование производной в любой точке рассматриваемого интервала.

Наглядно представить понятие производной можно с помощью графика:

Данные формулировки допустимы только при существовании рассматриваемых пределов.

Как найти производную?

Пример 1

f(x) = 6x³

f′(x) = 3 * 6x²

f′(x) = 18x²

Степень от x спускается и из неё нужно вычесть 1.

Пример 2

f(x) = 3x³ – 5x² + 6x − 5

f'(x) = 3*3x² – 2*5x¹ + 6 − 0

f(x) = 9x² – 10x + 6

Пример 3

f(x) = (x−4) (2x+x²)

Нужно сначала раскрыть скобки:

f(x) = (x−4) (2x+x²)=

f(x) = 2x² − 8x + x³ − 4x²

f(x) = x³ − 2x² − 8x

Теперь можно приступать к поиску производной, как и в предыдущих примерах степень от x спускается и из неё нужно вычесть 1:

f´(x) = (x³ − 2x² − 8x)´=

f´(x) = 3x² − 2*2x¹ − 8 =

f´(x) = 3x² − 4x − 8

Пример 4

f(x) = √x

Переведём сначала корень в степень:

f(x) = x ^ (½)

Теперь можно производить вычисления производной с обычной формулой степеней:

f´(x) = ½ * x ^ (½ – 1)

f´(x) = ½ * x ^ (– ½)

f´(x) = ½ * (1/√x)

Можно остановиться здесь, но бывает, что ответ с корнем в знаменателе не считается совсем правильным, поэтому умножаем всю вторую дробь на «√x/√x».

(1/√x) * (√x/√x) = √x/x

Значит правильный и «красивый» ответ:

f´(x) = ½ * (√x/x)

Пример 5

f(x) = sin x − cos x

Из таблицы мы знаем:

(sin x)´ = cos x

(cos x)´ = − sin x

Так как это вычитание, осталось только подставить:

f´(x) = (sin x − cos x)´

f´(x) = cos x − (− sin x)

f´(x) = cos x + sin x

(u (v))´ = u´ (v) * v´

Пример

1. Сначала нужно разобраться, что «arctg x» является нашей простой (внутренней) частью функции, это наше “v” формулы.

2. Применяем формулу корня из таблицы в левой части, получится 1/2 √arctg x, оставляя правую нерешённой.

3. Применяем формулу arctg x из таблицы (1/ (1 + x²)).

4. Совмещаем и готово

4.1. Если хотите «красивый» ответ, нужно убрать корень из знаменателя, умножая всю эту дробь на √arctgx / √arctgx.

Получится √arctgx / (2 (1 + x²) arctgx)

Как определить знак производной?

1. Определить точки, в которых производная равна нулю (также называются критическими точками).

2. Начертить таблицу, в которую вставляются все критические точки, а между ними оставляются незаполненными по одному окошку.

3. Выбрать значения x до и после полученного интервала, подставить в производную. Если значение получилось больше нуля, то знак будет плюс, если меньше — минус.

Пример:

y = x² – 6x + 17

Её производная y’ = 2x – 6.

Расчёт критических точек:

y’ = 0

2x – 6 = 0

2x = 6

x = 3

Значит в нашей таблице будет только одна критическая точка x = 3, и оставим место на «до» и «после».

x < 3	x = 3	x > 3

Далее выбираем любой x сначала меньше 3, а потом больше 3.

1. для x < 3 выбираем, например, x = 1 и подставляем в производную y’ = 2x – 6 ⇔ y’(1) = 2 * 1 – 6 = -4 <0, значит в таблицу записываем «–» (это означает, что в этой точке функция убывает).

2. для x > 3 выбираем, например, x = 4 и подставляем в производную y’ = 2x – 6 ⇔ y’(4) = 2 * 4 – 6 = 2 >0, значит в таблицу записываем «+» (это означает, что в этой точке функция возрастает).

x < 3	x = 3	x > 3
–	+

Производная и угловой коэффициент касательной

Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.

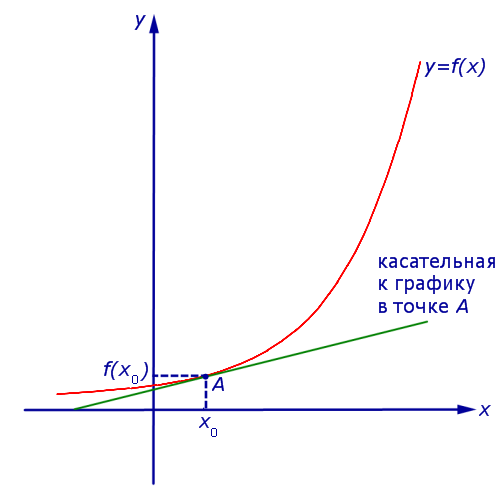
В случае, когда при $x_1\;\rightarrow\;x_0$ имеется предельное положение секущей графика функции $y = f(x)$, оно будет носить название касательной к графику функции $y = f(x)$ в точке $A\;=\;((x_0;\;f(x_0))$. А значение производной в точке касания $x_0$ будет эквивалентно угловому коэффициенту касательной.

Угловой коэффициент касательной равен значению производной в точке касания $x_0$. И в соответствии с тем, что касательная параллельна прямой $y = -x$, ее угловой коэффициент равен -1.

Геометрический смысл производной состоит в том, что производная в точке $x_0$ равна угловому коэффициенту касательной к графику функции $y = f(x)$ в этой точке.

Формула уравнения касательной к графику функции $y = f(x)$ в точке $x_0$ выглядит следующим образом:

$y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)$

Рассмотрим рисунок графика функции $y = f(x)$. Очевидно, что для каждой из точек $A$ и $B$ графика функции справедливо следующее разностное отношение:

$\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha$

Здесь $\alpha$ — угол между прямой и осью $ОХ$, а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке $A$.

Зафиксируем точку $A$ и будем продвигать точку $B$ в направлении к ней. Тогда $\triangle x$ бесконечно уменьшается и приближается к 0, а секущая $АВ$ приближается к касательной $АС$.

Пример

Необходимо записать уравнение касательной к графику функции $y=x+e^{-2x}$, если эта функция параллельна прямой $y = -x.$

При условии, что касательная параллельна прямой $y = -x$, справедливо утверждение об эквивалентности углового коэффициента $-1$. Этот вывод можно сделать из эквивалентности углового коэффициента касательной значению производной в точке касания $х_0$. Таким образом $f'(x0) = -1$.

$f'(x_0)\;=\;(x_0\;+\;e^{-2x_0})’\;=\;1\;-\;2e^{-2x_0}\\1\;-\;e^{-2x_0}\;=\;-1\\2e^{-2x_0}\;=2\\e^{-2x_0}\;=\;1\\-2x\;=\;0\\x_0\;=\;0$

Используем уравнение касательной

$y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x$

40.421. Смысл производной

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Уравнение касательной в точке $ x_{0} $ выглядит следующим образом:

$ y=f'(x_{0})x-f'(x_{0}) \cdot x_{0}+f(x_{0}) $

$ f'(x_{0}) $ — значение производной в точке $ x_{0} $ $ x_{0} $ — координата самой точки $ f(x_{0}) $ — значение функции в точке $ x_{0}$

Производная функция в точке $ x_{0}$ равно коэффициенту наклона касательной, проведённая в точке $ x_{0}$$ f'(x_{0})=k=tg \; a $

Функция возрастает$ tg \; a>0 $

Функция убывает$ tg \; a

Экстремум$ tg \; a=0 $

Отсюда можно сделать несколько выводов о том, как связаны значение производной и поведение функции:

1. Функция возрастает.

Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный (k > 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.

Функция возрастает $ \Rightarrow f'(x_{0})>0 $

2. Функция убывает.

Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k

Функция убывает $ \Rightarrow f'(x_{0})

3. Экстремум.

Точки экстремума, отличаются тем, что в них функция и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше).

Функция возрастает $ \Rightarrow f'(x_{0})=0 $

Точка максимума

До неё функция возрастает, после него убывает. В точке максимума производная сменяет свой знак с плюса на минус.

Максимум: $ f'(x_{0}) + \Rightarrow — $

Точка минимума

До неё функция убывает, после него возрастает. В точке минимума производная сменяет свой знак с минуса на плюс.

Максимум: $ f'(x_{0}) — \Rightarrow + $

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ:

Допустим есть некоторая точка, которая двигается вдоль оси ОХ, и ее координата меняется со временем по закону $ x(t) $. Получается, что $ x(t) $ – это функция того, как меняется расстояние.

Мы знаем определение производной: это темп изменения функции. Если говорить про темп изменения расстояния, то можно догадаться, что это скорость.

То есть:

Чтобы найти скорость материальной точки, необходимо взять производную от функции координаты:

$ v(t)=x'(t) $

Темп изменения скорости – это ускорение. Поэтому:

Чтобы найти ускорение, необходимо взять производную от функции скорости, то есть вторую производную от координаты:

$ a(t)=v'(t)=x»(t) $

Таким образом, скорость материальной точки – это первая производная от функции расстояния (координаты), а ускорение – вторая производная от функции расстояния.

Прочитано
Отметь, если полностью прочитал текст

Правила вычисления производных с формулами

Перечислим справедливые закономерности, которые следует использовать в процессе вычисления производной функции, то есть при выполнении дифференцирования:

Постоянную переносят за знак производной таким образом: ${{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’$.
Производную от некоторой суммы можно вычислить с помощью формулы: ${{\left( f+y \right)}^{\prime }}={f}’+{y}’$.
Производную от умножения допустимо рассчитывать следующим способом:${{\left( f\cdot y \right)}^{\prime }}={f}’\cdot y+f\cdot {y}’$ .
Производную от деления целесообразно вычислять с помощью соотношения: ${{\left( \frac{f}{y} \right)}^{\prime }}=\frac{{f}’y-f{y}’}{{{y}^{2}}}$.
Производная в случае вычислений сложной функции определяется таким образом: ${{\left}^{\prime }}={f}’\left( y \right)\cdot {y}’$.

В процессе выполнения расчетов различных задач и примеров важно исключить ошибки в действиях. С этой целью полезно использовать простой алгоритм операций, позволяющий достаточно просто дифференцировать сложные функции:

Выявить функцию, которая записана внутри выражения, и определить, чему равна ее производная.
Записать функцию, расположенную снаружи, и аналогично выполнить ее дифференцирование.
Перемножить полученные значения после выполнения первого и второго этапа вычислений.

Знак производной на интервалах возрастания

Определим, какая функция называется возвращающей.

$y = f(x)$ будет возрастать на интервале $X$, если для любых $x_1\;\in\;X$ и $x_2\;\in\;X$, где $x_2\;>\;x_1$, справедливо неравенство $f(x_2)\;\geq\;f(x_1)$.

В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид $f(x_1) < f(x_2)$, функция $y = f(x)$ будет называться строго возрастающей на интервале $(a, b)$.

На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.

В тех случаях, когда производная функции $y = f(x)$ положительна для любого x из интервала $X$, функция возрастает на $X$.

Производная

Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями?

Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции.

Почему функции похожи на американские горки? Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.

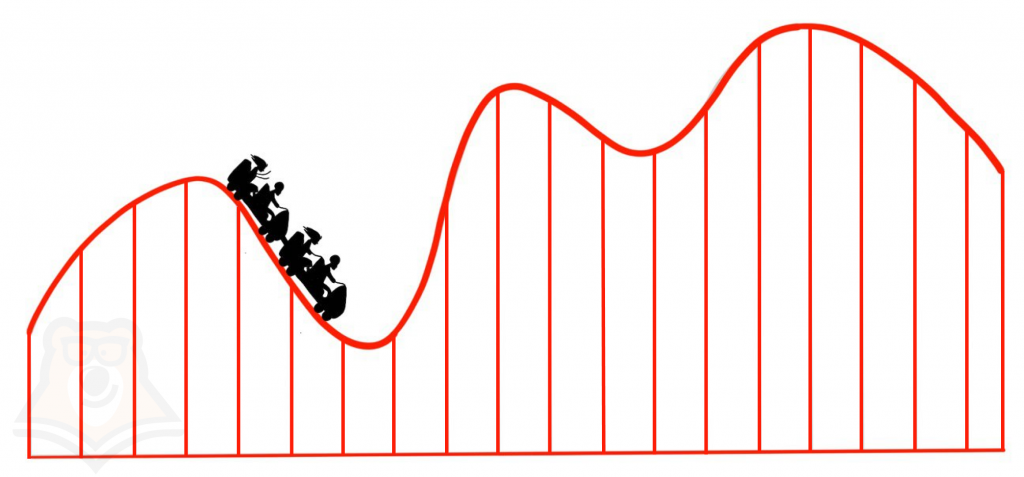
Представим наши американские горки в виде функции.

Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной.

Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х).

Отложим на нашем графике две точки: х и х₁ и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х₁;у₁).

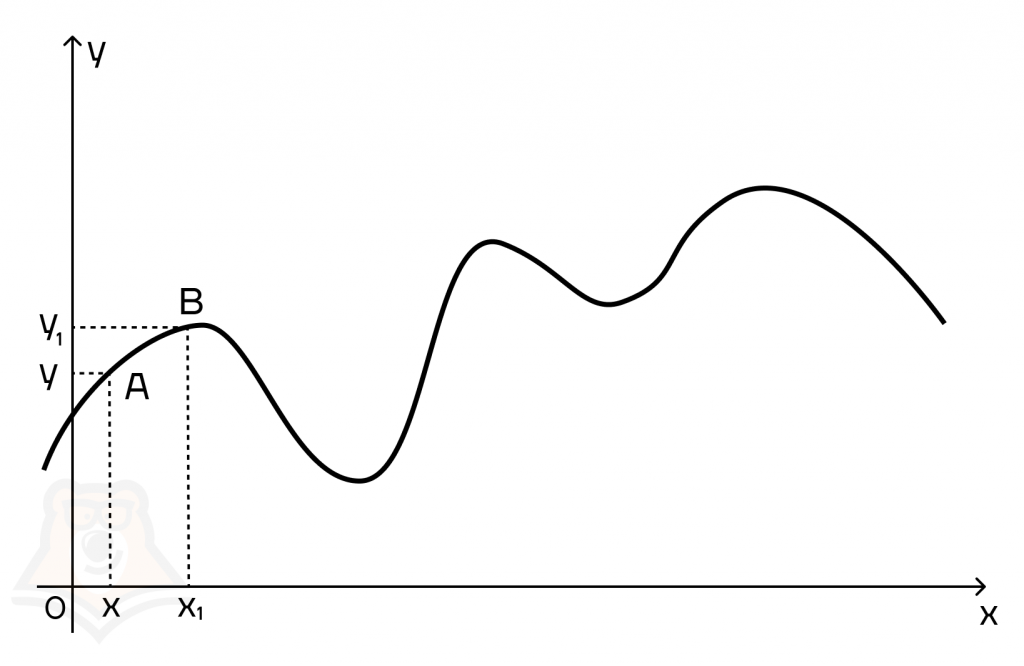
Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х₁— х, а поднялся он на высоту у₁— у. Для удобства дальнейших рассуждений примем эти расстояния за х и у.

Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.

Теперь мы можем ввести определение приращения.

Приращение функции — это разность между двумя значениями функции, то есть у.

Приращение аргумента — это разность между двумя значениями аргумента, то есть х.

Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.

Отсюда мы получаем определение производной функции.

Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции.

Производную функции обозначают как f'(x).

$f'(x) = \frac{\Delta y}{\Delta x}\: при\: \Delta x \rightarrow 0$

Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках.

Нахождение производной называется дифференцированием.

Как с помощью производной оценить рост популярности видео в соцсети?Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати. Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр. В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени.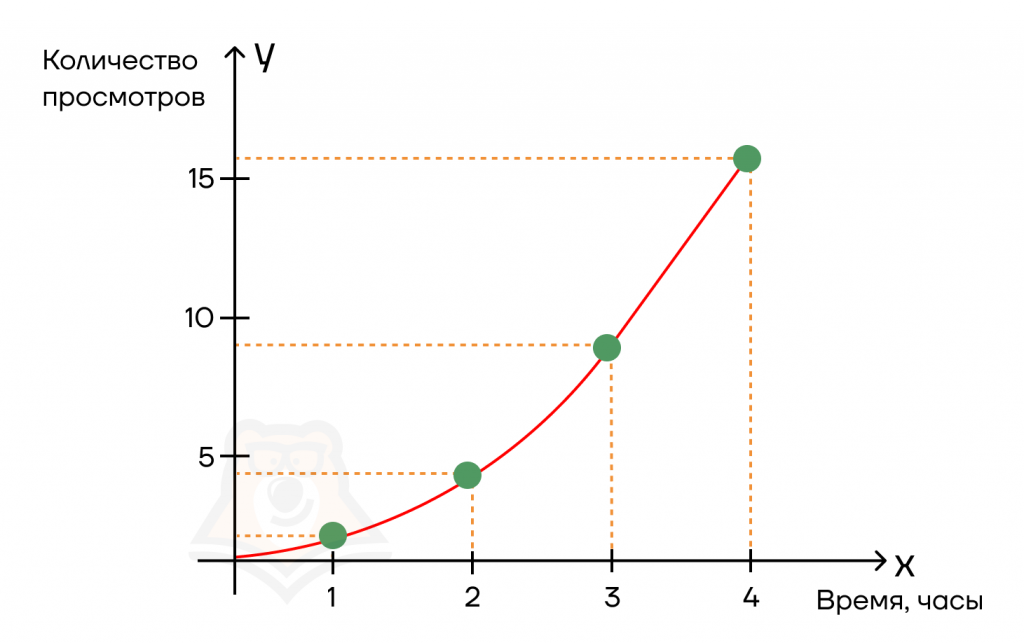

Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);2) как изменилось время между этими точками (Δ времени);3) затем разделим Δ просмотров на Δ времени.

Получается, что “производительность” нашего видео была 5 просмотров в час. Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:$f'(x) = \frac{\Delta y}{\Delta x} = \frac{5}{1} = 5$(просмотров в час)

Пример № 2

Материальная точка движется по закону:

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

Функция f(x) называется возрастающей на отрезке если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
Функция f(x) называется убывающей на отрезке если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Как обычно, перечертим график и отметим границы , а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Избавимся от лишней информации. Оставим только границы и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:l₁ = − 6 − (−8) = 2;l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

ЕГЭ 2022, задание 6. Касательная к графику функции
ЕГЭ 2022, задание 6. Касательная к графику функции
Схема Бернулли. Примеры решения задач
Решение задач B6: №362—377
Четырехугольная пирамида: как найти координаты вершин
Нестандартная задача B2: студенты, гонорары и налоги