Перевод десятичной дроби в обыкновенную

Советы

• Убедитесь, что десятичная дробь имеет простейшую форму, прежде чем преобразовывать ее в дробь. Например, если десятичное число равно 0,75, перед преобразованием упростите его до 3/4. Такие значения как 0,5=1/2, 0,25=1/4 и 0,75=3/4 лучше запомнить, так как они часто встречаются.
• Когда десятичная дробь имеет целое число, запишите ее как неправильную дробь, прежде чем преобразовывать в обыкновенную дробь. Например, 1,5 можно записать как 15/10 перед преобразованием.
• При преобразовании периодичных десятичных дробей в обыкновенные дроби полезно распознавать закономерности в цифрах. Например, 0,44444….=0,(4) можно распознать как дробь с периодической частью (4), поэтому её можно записать как 4/9. Перевод периодичной десятичной дроби в обыкновенную всегда можно осуществлять так, например, 0,(167) будет 167/999.
• Если десятичное число имеет завершающее десятичное расширение (то есть оно заканчивается после определенного количества знаков после запятой), его можно преобразовать в дробь, поместив в знаменателе число 10 в степени, равной количеству знаков после запятой. Например, 0,25 можно записать как 25 /102, что упрощается до 1/4 или 0,456723=456723/106=456723/1000000.

Примеры перевода из десятичной дроби в обыкновенную

Пример 1

Преобразовать 0,32 в обыкновенную дробь:

Решение: запишем 0,32 = 32/100

Найдем наибольший общий делитель (НОД) числителя и знаменателя:

НОД(32, 100) = 4

Сократим дробь, разделив числитель и знаменатель на НОД:

0,32 = (32/4)/(100/4) = 8/25

Ответ: 8/25

Пример 2

Преобразовать 2,56 в дробь:

2,56 = 2 + 56/100

Решение: найдите наибольший общий делитель (НОД) числителя и знаменателя:

НОД(56, 100) = 4

Сократите дробь, разделив числитель и знаменатель на НОД:

\displaystyle 2 + \frac{56}{100} = 2 + \frac{56/4}{100/4} = 2 + \frac{14}{25}

Ответ: \displaystyle 2 \frac{14}{25}

Пример 3
Преобразовать 0,124 в дробь:

0,124 = 124/1000

Найдите наибольший общий делитель (НОД) числителя и знаменателя:

НОД(124,1000) = 4

Сократите дробь, разделив числитель и знаменатель на НОД:

0,124 = (124/4)/(1000/4) = 31/250

Как преобразовать повторяющиеся десятичные дроби в дроби
Пример 1
Преобразовать 0,333333… в дроби:

х = 0,333333…

10 х = 3,333333…

10 х — х = 9 х = 3

х = 3/9 = 1/3

Пример #2
Преобразовать 0,0565656… в дроби:

х = 0,0565656…

100 х = 5,6565656…

100 х — х = 99 х = 5,6

990 х = 56

х = 56/990 = 28/495

Преобразование десятичных дробей в дроби для бесконечных периодических десятичных дробей

Чтобы преобразовать повторяющуюся десятичную дробь в простую дробь, выполните следующие действия.

Напишите уравнение, в котором переменная (например, x) равна десятичному числу с повторяющимися цифрами после запятой, включенными только один раз. Например, если у вас есть десятичное число \$5,61111\ldots=5,6\bar{1}\$, уравнение должно выглядеть следующим образом:

$$x=5,6\bar{1}$$

Определите количество цифр в повторяющейся десятичной группе (n) и умножьте обе стороны уравнения на \${10}^n\$. В нашем случае есть только одна повторяющаяся цифра: 1. Поэтому обе стороны уравнения нужно умножить на \${10}^1=10\$:

$$10x=56,1\bar{1}$$

Вычтите первое уравнение из второго. В нашем примере мы получаем:

$$10x=56,1\bar{1}$$

$$x=5,6\bar{1}$$

$$9x=50,5$$

Проводя вычисления для x, мы получаем:

$$x=\frac{50,5}{9}$$

Чтобы избавиться от десятичных знаков, умножьте числитель и знаменатель числа на 10 в степени n, где n — количество цифр после запятой. В нашем случае после запятой стоит только одна цифра — 5. Поэтому нам нужно умножить на 10:

$$\frac{50,5}{9}×\frac{10}{10}=\frac{505}{90}$$

Найдите наибольший общий коэффициент числителя и знаменателя полученной дроби и уменьшите дробь, разделив числитель и знаменатель на GCF. В нашем случае GCF равен 5, поэтому:

$$\frac{505\div5}{90\div5}=\frac{101}{18}$$

Упростите неправильную дробь:

$$\frac{101}{18}=5\frac{11}{18}$$

В итоге, \$5,6\bar{1}=5\frac{11}{18}\$.

Таблица перевода дроби в десятичную

Доля	Десятичная дробь
1/2	0,5
1/3	0,33333333
2/3	0,66666667
1/4	0,25
2/4	0,5
3/4	0,75
1/5	0,2
2/5	0,4
3/5	0,6
4/5	0,8
1/6	0,16666667
2/6	0,33333333
3/6	0,5
4/6	0,66666667
5/6	0,83333333
1/7	0,14285714
2/7	0,28571429
3/7	0,42857143
4/7	0,57142858
5/7	0,71428571
6/7	0,85714286
1/8	0,125
2/8	0,25
3/8	0,375
4/8	0,5
5/8	0,625
6/8	0,75
7/8	0,875
1/9	0,11111111
2/9	0,22222222
3/9	0,33333333
4/9	0,44444444
5/9	0,55555556
6/9	0,66666667
7/9	0,77777778
8/9	0,88888889
1/10	0,1
2/10	0,2
3/10	0,3
4/10	0,4
5/10	0,5
6/10	0,6
7/10	0,7
8/10	0,8
9/10	0,9
1/11	0,09090909
2/11	0,18181818
3/11	0,27272727
4/11	0,36363636
5/11	0,45454545
6/11	0,54545454
7/11	0,63636363
8/11	0,72727272
11 сентября	0,81818181
10/11	0,90909091

Преобразование десятичных дробей в простые дроби

Чтобы преобразовать десятичную дробь в простую дробь или смешанное число, выполните следующие действия.

Любое десятичное число x можно представить в виде дроби с 1 в знаменателе \$\frac{x}{1}\$. В качестве первого шага перепишите данное число в виде дроби, где числителем будет само число, а знаменателем — 1.

Затем подсчитайте количество цифр после запятой и умножьте числитель и знаменатель на 10 в соответствующей степени. Если ваше число имеет n цифр после запятой, то числитель и знаменатель дроби нужно умножить на \${10}^n\$.

Найдите наибольший общий коэффициент числителя и знаменателя полученной дроби и уменьшите дробь, разделив числитель и знаменатель на наибольший общий коэффициент.

Если после упрощения у вас получилась неправильная дробь, преобразуйте ее в смешанное число.

Особенности калькулятора дроби в десятичную дробь

Калькулятор дробей в десятичные числа, предлагаемый cmtoinchesconvert.com, представляет собой бесплатную онлайн-утилиту, которая позволяет пользователям конвертировать калькулятор дробей в десятичные числа без каких-либо ручных усилий.Ниже перечислены некоторые из ключевых особенностей этого калькулятора дробей для десятичных дробей:

100% бесплатно

Вам не нужно проходить какой-либо процесс регистрации, чтобы использовать этот калькулятор преобразования дробей в десятичные числа.Вы можете использовать эту утилиту бесплатно и выполнять неограниченное количество преобразований калькулятора дробей в десятичные числа без каких-либо ограничений.

Легко доступный

Вам не нужно устанавливать какое-либо программное обеспечение на свое устройство, чтобы получить доступ к калькулятору дробей в десятичную дробь.Вы можете получить доступ и использовать этот онлайн-сервис с помощью любого веб-браузера со стабильным подключением к Интернету.

Удобный интерфейс

Калькулятор дроби в десятичную систему представляет собой простой в использовании интерфейс.Используйте это, чтобы пользователи могли конвертировать фракцию в десятичный онлайн-калькулятор за считанные секунды.Вам не нужно приобретать какие-либо специальные навыки или выполнять сложные процедуры, чтобы использовать этот калькулятор дроби в десятичную дробь.

Быстрая конвертация

Калькулятор десятичных дробей предлагает пользователям самое быстрое преобразование.После того, как пользователь введет значения Калькулятора дробей в десятичные числа в поле ввода и нажмет кнопку «Преобразовать», утилита начнет процесс преобразования и немедленно вернет результаты.

Точные результаты

Результаты, полученные с помощью этого калькулятора дробей и десятичных дробей, точны на 100%.Передовые алгоритмы, используемые этой утилитой, обеспечивают пользователям безошибочные результаты.Если вы уверены в подлинности результатов, предоставляемых этой утилитой, вы можете использовать любой метод для их проверки.

Совместимость

Калькулятор дробей в десятичные дроби совместим со всеми типами устройств.Независимо от того, используете ли вы смартфон, планшет, настольный компьютер, ноутбук или Mac, вы можете легко использовать этот калькулятор дроби в десятичную дробь.

Как перевести обычную дробь в десятичную

Прежде чем мы научимся переходить с обычного на десятичное представление, давайте вспомним различия между двумя типами дробей и сформулируем важное правило. Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42

А вот так выглядят те же числа в виде правильных дробей:

Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А вот так выглядят те же числа в виде правильных дробей:

Обыкновенная дробь может быть преобразована в конечную десятичную дробь только в том случае, если знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:

Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель делится на 2 и 5.

Дробь 17/60 нельзя перевести в конечную десятичную дробь, потому что в знаменателе, кроме множителей 2 и 5, стоит 3.

А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов преобразования обыкновенной дроби в десятичную.

Алгоритм преобразования

Акт преобразования десятичной дроби в простую относится к элементарным операциям. Есть несколько способов перевода. Какой из них выполнить, зависит от личных предпочтений лица, принимающего решение. Например, выражение 3.2 также можно записать как 16/5.

Другими словами, математики договорились, что, когда речь идет о простых числах, нули опускаются, а вместо них ставится запятая, отделяющая целую часть. Это было сделано для облегчения восприятия записи и для удобства подсчета.

Правило для наиболее часто используемого метода перевода заключается в следующем. Если в знаменателе стоит число, кратное десяти, нужно просто переписать числитель, затем подсчитать количество цифр, совпадающих с числом в знаменателе, и поставить после них запятую. Подсчет количества разделенных цифр необходимо начинать с правой стороны. Также, если количество нулей превышает количество цифр в делителе, то пропущенное их количество пишется перед числом.

Выполняемые операции, кроме получения периодической дроби, можно производить и в обратном направлении. Остаток от деления всегда должен быть меньше делителя. Поэтому, если в результате действия получается нуль, деление останавливается, а если в остатке — бесконечное периодическое отношение.

Чаще всего для преобразования простой дроби в десятичную нужно выполнить три шага:

1. Сократите выражение, которое необходимо преобразовать.
2. Разделите числитель на знаменатель практичным способом. В зависимости от размера значений в числителе и знаменателе это можно сделать в столбце или в баках. Если при делении получается ненулевой остаток, поставьте запятую и продолжайте искать частное.
3. Запишите найденный результат через запятую.

Способ 1. Превращаем знаменатель в 10, 100 или 1000

Чтобы преобразовать дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число так, чтобы знаменатель стал равен 10, 100, 1000 и т д. Но прежде чем продолжить расчеты, необходимо проверить, можно ли преобразовать это дробь вообще в десятичную.

Возьмем, к примеру, дробь 3/20. Его можно сократить до последнего десятичного знака, потому что знаменатель делится на 2 и 5.

Мы можем получить 100 внизу: просто умножьте 20 на 5. Не забывайте и о верхней части: мы получаем 15.

Теперь напишем счетчик отдельно. Отсчитываем справа столько знаков, сколько нулей в знаменателе, и ставим запятую. В нашем примере знаменатель равен 100 (в нем два нуля), поэтому после подсчета двух цифр ставим запятую и получаем 0,15. Трансформация готова.

Другой пример:

Способ 2. Делим числитель на знаменатель

Чтобы преобразовать обыкновенную дробь в десятичную, достаточно разделить верхнюю часть на меньшую. Проще всего это сделать, конечно, с помощью калькулятора — но его не разрешают использовать в тестах, поэтому мы учимся по-другому.

Возьмем, к примеру, дробь 78/100. Давайте удостоверимся, что дробь можно сократить до последнего десятичного знака.

Делим числитель на знаменатель столбиком — преобразование готово:

Если при делении на угол выяснилось, что процесс не заканчивается и повторяющиеся числа выстраиваются в ряд после запятой, то эту дробь нельзя преобразовать в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно в скобках записать повторяющееся число, вот так: 1/3 = 0,3333.. = 0, (3).

Для простоты мы составили таблицу дробей со знаменателями, которые чаще всего встречаются в математических задачах. Загрузите его на свой гаджет или распечатайте и сохраните в учебнике как закладку:

Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс преобразования десятичной дроби в обычный процент. Сформулируйте правило преобразования, состоящее из трех шагов. Как преобразовать десятичные дроби в дробные?

Правила преобразования десятичных дробей в дробные.

1. В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
2. В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
3. При необходимости сокращаем полученную обыкновенную дробь.

Рассмотрим применение этого правила на примере.

Пример 8.Преобразование дробных дробей в десятичные дроби

Преобразуйте 3,025 в дробь.

1. В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
2. В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
3. Полученную дробь 3025 1000 можно сократить на 25, в результате чего мы получим: 3025 1000 = 121 40 .

Переведите десятичные дроби 0 и 0017 из десятичной системы счисления в обычную.

1. В числителе запишем дробь 0, 0017, отбросив запятую и нули слева. Получится 17 .
2. В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000. Данная дробь несократима.

Если в дробной дроби есть целое число, то дробь можно сразу преобразовать в смешанное число. Как это может произойти?

Давайте сформулируем другое правило.

Правило преобразования десятичной дроби в смешанное число.

1. Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
2. В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
3. В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Пример 10.Преобразование дробных дробей в смешанные числа

Пусть 155 и 06005 представлены в виде смешанных чисел.

1. Записываем число 155, как целую часть.
2. В числителе записываем цифры после запятой, отбросив нуль.
3. В знаменателе записываем единицу и пять нулей

Возьмите смешанное число: 155,6005,100000.

Дробная часть может быть уменьшена на 5. Уменьшите его и получите конечный результат.

155, 06005 = 155 1201 20000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Рассмотрим пример дроби, преобразованной в повторяющуюся десятичную дробь. Прежде чем начать, давайте заявим, что каждая дробь может быть преобразована в обычную дробь.

В простейшем случае период дроби равен нулю. Дробь с нулевым периодом заменяется десятью десятичными знаками, и процесс преобразования таких дробей возвращается к преобразованию конечных дробей.

Пример 11.Преобразование дробных дробей в обычные дробные дроби

Преобразуйте периодическую дробь 3, 75 (0).

Используя нули справа, вы получите конечную десятичную дробь 3, 75.

Следуя алгоритму, описанному в предыдущем пункте, преобразуя эту дробь в обычную дробь, получаем

3, 75 (0) = 3, 75 = 375 100 = 15 4.

Что произойдет, если дробный период будет ненулевым? Периодические фракции следует рассматривать как сумму условий для сокращения геометрической прогрессии. Давайте проиллюстрируем это на примере.

Как ввести повторяющиеся десятичные знаки

Повторяющиеся десятичные знаки после запятой — это цифры после десятичного знака, которые бесконечно повторяются в числе.

Например, предположим, вам нужно ввести повторяющуюся десятичную дробь \$0,333\ldots=0,\bar{3}\$. В этом случае сначала нужно ввести 0,3 в поле «Введите десятичное число», а затем ввести 1 во второе поле ввода, так как это число имеет только один последующий десятичный знак — 3. (Ответ будет \$\frac{1}{3}\$).

Если вам нужно ввести повторяющуюся десятичную дробь, например \$0,454545\ldots=0,\bar{45}\$, сначала введите 0,45 в поле «Введите десятичное число», а затем введите 2 во второе поле, так как это число имеет два повторяющихся десятичных знака — 45. (Ответ будет \$\frac{5}{11}\$).

Если вам нужно ввести десятичную дробь, например, \$2,83333333\ldots=2,8\bar{3}\$, сначала введите 2,83 в поле «Введите десятичное число», а затем введите 1 во второе поле ввода, так как это число имеет только один последующий десятичный разряд — 3. (Ответ будет \$2\frac{5}{6}\$).

Для десятичной дроби, например \$0,285714285714\ldots=0,\bar{285714}\$, сначала введите 0,285714 в поле «Введите десятичное число», а затем введите 6 во второе поле ввода, так как это число имеет шесть идущих после запятой знаков — 285714. (Ответ будет \$\frac{2}{7}\$).

Калькулятор принимает в качестве входных данных как положительные, так и отрицательные десятичные числа.

После ввода десятичной дроби и количества идущих после запятой знаков калькулятор выполнит преобразование в дробь или смешанное число и отобразит ответ, а также подробное объяснение решения.

Метод преобразования 0,25 в обыкновенную дробь

Шаг 1: В числе после запятой количество цифр определяет количество десятичных знаков в обыкновенной дроби. В данном случае после запятой стоят две цифры, поэтому знаменатель будет 100.

Шаг 2: Чтобы найти числитель, нужно умножить десятичную дробь на 100. В этом случае получим 25. Таким образом, обыкновенная дробь будет равна 25/100.

Шаг 3: Данную обыкновенную дробь можно сократить, найдя их наибольший общий делитель (НОД). В данном случае 25 и 100 имеют НОД равный 25. Поделив числитель и знаменатель на 25, получим окончательный результат — 1/4.

Таким образом, десятичная дробь 0,25 эквивалентна обыкновенной дроби 1/4.

Правила перевода из десятичной дроби в обыкновенную

Чтобы преобразовать десятичную дробь в обыкновенную, выполните следующие действия:

• Запишите десятичную дробь с десятичным значением в качестве числителя и степенью числа 10 в качестве знаменателя. Например, если десятичная дробь равна 0,5, запишите ее как 5/10, если 0,05 то как 5/100 и так далее.
• Упростите дробь, разделив числитель и знаменатель на их наибольший общий делитель. Например, наибольший общий делитель 5 и 10 равен 5, поэтому мы можем упростить 5/10 до 1/2, разделив и числитель, и знаменатель на 5.
• Если в десятичной дроби есть повторяющиеся цифры, запишите повторяющиеся цифры в качестве числителя дроби и число девяток в качестве знаменателя. Подсчитайте количество повторяющихся цифр, чтобы определить количество девяток. Например, если десятичное число равно 0,333…, запишите его как 333/999.
• Упростите дробь, разделив числитель и знаменатель на их наибольший общий делитель.

Следуя этим правилам, вы можете преобразовать любую десятичную дробь в обыкновенную.

Основные показатели и свойства десятичных дробей

Как и любое математическое действие, формула дроби имеет свои основные свойства и характеристики, которые выделяют ее среди других. Десятичное уравнение отличает одним из основных правил, где указывается, что если с правой стороны получившегося числа приписывается один или несколько нулей, то ее показатель остается неизменным, что позволяет не использовать их. Например, если у человека есть 0,500000, тогда он может просто записать результат, как 0,5. Кроме того, формула характеризуется дополнительными показателями, среди которых стоит отметить следующие:

• Если делитель в формуле будет равняться показателю 0, тогда у нее не будет значения.
• Две дроби, например ½ и ¾ будут равны друг к другу, если их можно расписать по формуле 1х3 = 2х4.
• В случае, когда числитель приравнивается 0, а знаменатель будет представлен в виде обычного числа, тогда вся дробь будет равно 0.
• Когда числительное и знаменательные числа можно умножить или разделить на одно и то же самое число, тогда можно получить равную дробь.

Важно отметить, что когда речь заходит о переводе десятичной дроби в обыкновенную или наоборот, необходимо помнить, что они связаны между собой. Например, части обеих формул равны друг к другу, и если окажется, что числительные показатель будет меньше знаменательного, тогда целый результат будет приравниваться к нулю

Также стоит помнить, что количество нулей, которые пишутся после запятой, полностью соответствуют цифрам, указанным в дробном знаменателе, так 3 числа = 1000,/ 6 цифр = 1000000 и так далее.

Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?

Правило перевода десятичных дробей в обыкновенные дроби

1. В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
2. В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
3. При необходимости сокращаем полученную обыкновенную дробь. 

Рассмотрим применение данного правила на примерах.

Пример 8. Перевод десятичных дробей в обыкновенные

Представим число 3,025 в виде обыкновенной дроби.

1. В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
2. В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 30251000.
3. Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.

Пример 9. Перевод десятичных дробей в обыкновенные

Переведем дробь ,0017 из десятичных в обыкновенные.

1. В числителе запишем дробь ,0017, отбросив запятую и нули слева. Получится 17.
2. В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?

Сформулируем еще одно правило.

Правило перевода десятичных дробей в смешанные числа.

1. Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
2. В числителе  записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
3. В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Обратимся к примеру

Пример 10. Перевод десятичной дроби в смешанное число

Представим дробь 155,06005 в виде смешанного числа.

1. Записываем число 155, как целую часть.
2. В числителе записываем цифры после запятой, отбросив нуль. 
3. В знаменателе записываем единицу и пять нулей

Поучаем смешанное число: 1556005100000

Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:

155,06005=155120120000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.

Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример 11. Перевод периодической десятичной дроби в обыкновенную

Обратим периодическую дробь 3,75().

Отбросив нули справа, получим конечную десятичную дробь 3,75.

Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:

3,75()=3,75=375100=154.

Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:

,(74)=,74+,0074+,000074+,00000074+..

Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что <q<1, то сумма равна b1-q.

Рассмотрим несколько примеров с применением данной формулы.

Пример 12. Перевод периодической десятичной дроби в обыкновенную

Пусть у нас есть периодическая дробь ,(8) и нам нужно перевести ее в обыкновенную.

Запишем:

,(8)=,8+,08+,008+..

Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом ,8 и знаменателем ,1.

Применим формулу:

,(8)=,8+,08+,008+..=,81-,1=,8,9=89

Это и есть искомая обыкновенная дробь.

Для закрепления материала рассмотрим еще один пример.

Пример 13. Перевод периодической десятичной дроби в обыкновенную

Обратим дробь ,43(18).

Сначала записываем дробь в виде бесконечной суммы:

,43(18)=,43+(,0018+,000018+,00000018..)

Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:

,0018+,000018+,00000018..=,00181-,01=,0018,99=189900.

Полученное прибавляем к конечной дроби ,43=43100 и получаем результат:

,43(18)=43100+189900

После сложения данных дробей и сокращения получим окончательный ответ:

,43(18)=1944

В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Как записать 0,125 в обыкновенной дроби?

Чтобы записать десятичную дробь 0,125 в виде обыкновенной дроби, необходимо учесть, что каждая цифра после запятой соответствует десятичной степени в знаменателе дроби. В данном случае, цифра 1 стоит на третьем месте после запятой, следовательно, она будет в числителе дроби, а знаменатель будет равен 1000 (10 в степени 3).

Таким образом, дробь 0,125 можно записать как 1/8, где числитель равен 1, а знаменатель равен 8. Или, в виде таблицы:

Цифра	Десятичная степень
1	10 в степени -1
2	10 в степени -2
5	10 в степени -3

Таким образом, дробь 0,125 представляет собой одну восьмую (1/8) и может быть записана как обыкновенная дробь.

Пример вычисления для конечных десятичных дробей

Преобразуем десятичную дробь 0,125 в простую дробь. Следуя вышеописанным шагам, мы получим:

Представим число в виде дроби с 1 в знаменателе:

$$0,125=\frac{0,125}{1}$$

Это число имеет 3 цифры после запятой: 125. Поэтому нам нужно умножить числитель и знаменатель на \${10}^3\$:

$$\frac{0,125}{1}×\frac{1000}{1000}=\frac{125}{1000}$$

Наибольший общий множитель числителя и знаменателя равен 125. Поэтому, чтобы упростить эту дробь, нужно разделить числитель и знаменатель на 125:

$$\frac{125\div125}{1000\div125}=\frac{1}{8}$$

Это уже правильная дробь. Поэтому дальнейшее упрощение не требуется.

Ответ: \$0,125=\frac{1}{8}\$

Как записать 0,25 в обыкновенной дроби?

Десятичные числа можно записать в виде обыкновенной дроби, если мы представим их в разложенном виде. Давайте рассмотрим, как записать число 0,25 в виде обыкновенной дроби.

Для начала, мы знаем, что цифра «2» в числе 0,25 находится в разряде десятых, а цифра «5» — в разряде сотых. Таким образом, число 0,25 можно записать с помощью обыкновенной дроби, где в числителе будет 25, а в знаменателе будет степень десятки, соответствующая числу десятичных разрядов в исходном числе.

Таким образом, 0,25 равно 25/₁₀₀. Очень удобно представлять числа десятичных видах в виде обыкновенной дроби, так как это позволяет нам оценить их величину относительно других чисел и производить арифметические операции более удобным образом.

Основной алгоритм

На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.

Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:

1. Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:

   \

2. Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры:
   Алгоритм перехода к обычным дробям
3. Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25. Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)

Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус»

Вот ещё несколько примеров:

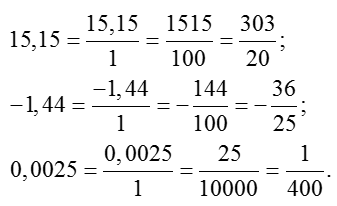Примеры перехода от десятичной записи дробей к обычной

Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой

Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?

Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.

Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

\

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

\

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

\

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Шаги по преобразованию десятичной дроби в обыкновенную форму

Преобразование десятичной дроби в обыкновенную форму может быть полезным, особенно при выполнении математических операций или представлении результатов в более удобной форме. Существует несколько шагов, которые можно выполнить, чтобы преобразовать десятичную дробь в обыкновенную форму.

1. Определите разрядность десятичной дроби: В первую очередь, нужно определить, сколько знаков после запятой присутствует в десятичной дроби. Например, в числе 0,125 есть три знака после запятой.
2. Преобразуйте десятичную дробь в дробь со знаменателем степени десяти: Знаменатель обыкновенной дроби будет равен 10, возведенному в степень числа знаков после запятой десятичной дроби. Например, для 0,125 знаменатель будет равен 10 в степени 3, то есть 1000.
3. Выполните деление числителя дроби: Числитель обыкновенной дроби будет равен значению десятичной дроби без запятой. Например, для 0,125 числитель будет равен 125.

Десятичная дробь	Знаменатель обыкновенной дроби	Числитель обыкновенной дроби	Результат
0,125	1000	125	125/1000
0,25	100	25	25/100
0,375	1000	375	375/1000
0,875	1000	875	875/1000

В результате преобразования, десятичная дробь записывается в обыкновенной форме, где числитель и знаменатель могут быть сокращены до наименьших целых чисел, если это возможно. Преобразование десятичной дроби в обыкновенную форму помогает упростить представление чисел и может быть полезным при сравнении или операциях с другими дробями.