Основные сведения о сложении чисел с разными знаками

Координатный луч

Чтобы определить координатный луч, нам сначала потребуется, конечно же, сам луч. Итак, построим луч, обозначим его OX, точка O – начало луча. Забегая вперед, скажем, что точку O называют началом отсчета координатного луча. Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.

Так у нас есть луч. Как же его сделать координатным лучом?

Во-первых, над точкой O нужно написать число .

Во-вторых, нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1.

В-третьих, на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному, далее от конца этого отрезка нужно отложить еще один единичный отрезок, от конца построенного отрезка нужно отложить еще один единичный отрезок, и так далее.

Наконец, чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из : 2, 3, 4, …

Так координатный луч представляет собой не что иное, как бесконечную шкалу.

Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа и 1. Этот вариант изображения координатного луча приведен на рисунке ниже.

В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.

Также допускается буквы O и X записывать над лучом, а числа – под лучом.

Наконец, не удивляйтесь, если в обозначении координатного луча Вы увидите одновременно и маленькую и большую буквы. Наиболее часто придется сталкиваться с координатными лучами, обозначенными как Ox, Oy и Oz.

Определение координат

Для того чтобы определить координаты точки, опускают перпендикуляр на каждую из осей. Получаются два отрезка. Значение длин этих отрезков в заданных единицах длины и будет соответствовать координатам точки.

Соответственно, чтобы по координатам построить точку, нужно провести перпендикуляр из заданных точек на осях. В точке пересечения этих перпендикуляров и будет находиться искомая точка.

У координатной плоскости есть 4 четверти, в каждой из которых свои границы х и у. Будьте внимательны, координаты вполне могут быть отрицательными. Это всего лишь позволяет определить четверть координатной плоскости.

Координатная прямая

Давайте внимательно рассмотрим шкалу термометра и постараемся схематично её изобразить. Шкала является прямой линией. Чертим её:

Замечаем, что каждое деление соответствует 1 градусу. Выходит, шкала имеет единичный отрезок.

Выбираем на нашем рисунке единичный отрезок не забывая, отложить его в обе стороны от начала отсчета:

Посмотрим на полученное изображение. Построенная геометрическая фигура имеет направление, точку начала отсчета и единичный отрезок. В математике, такие фигуры имеют свое название – координатная прямая.

Важным моментом, является то, что на координатной прямой по правую сторону от точки начала отсчета (0) находятся положительные числа, а по левой стороне – отрицательные (записанные со знаком «минус»).

На самом деле, на рисунке изображен небольшой фрагмент прямой. Данная линия продолжается в обе стороны до бесконечности, так как по определению, она не имеет ни начала, ни конца.

Формальное определение отрицательного числа

Су­ще­ству­ет еще один спо­соб по­яс­не­ния, что такое от­ри­ца­тель­ное число.

Для каж­до­го на­ту­раль­но­го числа, на­при­мер 5, вве­дем новое число, ко­то­рое обо­зна­чим (–5), и опре­де­лим, что оно об­ла­да­ет сле­ду­ю­щим свой­ством: сумма числа (–5) и 5 равна 0.

Число (–5) будем на­зы­вать от­ри­ца­тель­ным, а числа (–5) и 5 – про­ти­во­по­лож­ны­ми. Таким об­ра­зом, мы по­лу­чи­ли бес­ко­неч­ное ко­ли­че­ство новых чисел, на­при­мер:

(–1) – про­ти­во­по­лож­ное для числа 1;

(–10) – про­ти­во­по­лож­ное числу 10;

(–259) – про­ти­во­по­лож­ное числу 259;

(–1 000 000) – про­ти­во­по­лож­ное числу 1 000 000;

Вы­чтем из мень­ше­го числа боль­шее:

При­ба­вим к дан­но­му вы­ра­же­нию 5:

По­лу­чи­ли ноль. Од­на­ко, со­глас­но свой­ству: число, ко­то­рое в сумме с пятью дает ноль, обо­зна­ча­ет­ся минус пять (–5):

Сле­до­ва­тель­но, вы­ра­же­ние  можно обо­зна­чить как (–5):

Координата точки

Каждая точка, нанесенная на координатную прямую,всегда имеет свое числовое обозначение или координату.

Разберем на примере.

Построим координатную прямую. Нанесем начало отсчета и выберем единичный отрезок, равный 1 сантиметру. Обозначим деление буквой A:

Читается, точка A с координатой 1.

Нет ничего сложного!

Давайте применим на практике полученные знания и разберем задание.

Постройте координатную прямую и нанесите на неё точки:В(4), С(-2).

Чтобы выполнить данное задание необходимо изобразить прямую, выбрать на ней направление, точку начала координат и единичный отрезок, который будет равен 1 сантиметру.

Теперь нужно поставить точку В с координатой 4. Значение координаты точки положительное, поэтому отмечать её, будем с правой стороны от начала отсчета (0).Координата 4 говорит о том, что отметка В находится от нуля на расстоянии четырех единичных отрезков, то есть, расстояние от нуля до отметки В равно четырем сантиметрам.

Запомни! Положительные числа всегда расположены с правой стороны от нуля, а отрицательные числа с левой стороны от точки начала координат. В данном случае ноль и есть точка начала координат.

Строгие и нестрогие неравенства

Все неравенства, о которых мы говорили выше, называются «строгими». В чем же их строгость? Когда мы говорим \(x\) больше \(7\), то подразумеваем, что это неравенство будет верным при условии, что \(x\) принимает любые значения строго большие \(7\): \(8,100,100000\) и даже \(7,00001\), все эти числа больше семи. Но \(x=7\) не удовлетворяет этому неравенству. Так как \(7\) не больше \(7.\)

А что, если мы хотим показать, что \(x\) может принимать значения не только большие \(7\), но и равное \(7\)? Для таких случаев придумали знак «больше или равно», обозначается \(x \geq 7\).

Аналогичным образом существует знак «меньше или равно» \(x \leq 1\), который обозначает, что, если вместо \(x\) подставить значения меньшие единицы или равное единице, то неравенство будет верным.

Неравенства со знаками \(\geq\) или \(\leq\) называются «нестрогими». Пример таких нестрогих неравенств:
$$x \geq 12;$$
$$x \leq -1;$$
$$x\geq \frac{1}{6};$$

Часто с нестрогими неравенствами возникает путаница. Скажите, какие из представленных ниже неравенств верные, а какие нет:
$$3 \ge 2;$$
$$4 \ge 4;$$
$$5 \gt 5;$$
Первое неравенство будет верным: \(3\) действительно больше \(2.\) Второе неравенство тоже верное, так как знак неравенства \(«\ge»\) разрешает равенство, а \(4\) равно \(4.\) А вот третье неравенство неверное, потому что \(5\) не больше \(5,\) а знак неравенства строгий, равенство не допускается.

Нестрогие неравенства тоже можно изобразить графически на числовой прямой. Для того, чтобы различать на рисунке строгие и нестрогие неравенства, придумали обозначать строгие незакрашенной (выколотой) точкой, а нестрогие при помощи закрашенной.

На рисунке \(10\) показано строгое неравенство \(x \gt 8\). На рисунке \(11\): нестрогое \(x \geq 8\)

Обратите внимание на точку \(8\): в строгом неравенстве она выколотая, а в нестрогом закрашенная:

Положительные числа

В каждом доме и квартире есть термометр– незаменимый прибор для измерения температуры воздуха. Давайте внимательно его рассмотрим.

Мы видим шкалу, с нанесенными цифрами, которая расположена в стеклянной колбе. Стоит отметить, что шкала прибора разделена точно пополам делением с цифрой 0. Все цифры, находящиеся вверху от нуля имеют положительное значение и записываются со знаком «плюс».

Например: +18,+22,+3.

В арифметике такие значения имеют свое название – положительные.

Примеры положительных чисел: 5,18,39,156.

Исходя из рассмотренного правила, делаем вывод, что числа, перед которыми не стоит знак и числа со знаком «+» равны.

+8 = 8;

11 = +11;

+24 = 24;

Положительные числа можно использовать для выполнения любых математических действий:

сложения;

вычитания;

умножения;

деления;

возведения в степень.

Получается, что именно с положительными значениями вы знакомы с первого класса.

Размещаем фигуру

Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.

В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.

Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.

Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.

Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.

Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.

Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.

Что такое положительные и отрицательные числа

Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.

Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.

Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).

Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.

Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.

Мы всегда записываем отрицательные числа с минусом.

В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.

Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.

Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.

Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.

Примеры задач с решением

Задача 1

Задача

Нужно решить: (+3) + (+4)

Решение:

(+3) + (+4) = +7

Ответ: 7

Задача 2

Задача

Требуется решить: (-4) + (-3)

Решение:

(-4) + (-3) = -7

Ответ: -7

Задача 3

Задача

Необходимо выполнить сложение: (+15) + (-7)

Решение:

(+15) + (-7) = 15 — 7 = 8

Ответ: 8

Задача 4

Задача

Нужно выполнить вычитание: (+7) — (+4)

Решение:

(+7) — (+4) = +3

Ответ: 3

Задача 5

Задача

Требуется найти разность чисел: -17 — (-14)

Решение:

-17 — (-14) = -17 + 14 = -3

Ответ: -3

Задача 6

Задача

Необходимо решить пример: (+5) ⋅ (-8)

Решение:

(+5) ⋅ (-8) = -40

Ответ: -40

Задача 7

Задача

Нужно найти произведение двух чисел: -9 ⋅ (-9)

Решение:

-9 ⋅ (-9) = 81

Ответ: 81

Задача 8

Задача

Требуется решить пример: -6 ⋅ 5

Решение:

-6 ⋅ 5 = -30

Ответ: -30

Задача 9

Задача

Нужно выполнить деление двух чисел: 40 : (-8)

Решение:

40 : (-8) = -5

Ответ: -5

Задача 10

Задача

Требуется найти разность: (-6) — (+6) — (-8)

Решение:

(-6) — (+6) — (-8) = -12 — (-8) = -12 + 8 = -4

Ответ: -4

Задача 11

Задача

Необходимо решить пример:  (-5) ⋅ (-4) + (+3) ⋅ (-2)

Решение:

(-5) ⋅ (-4) + (+3) ⋅ (-2) = 20 + (-6) = 14

Ответ: 14

Задача 12

Задача

Нужно найти ответ: (-15) ⋅ : (+5)

Решение:

(-15) ⋅ : (+5) = -15 ⋅ (-18) : 5 = (-15 : 5) ⋅ (-18) = -3 ⋅ (-18) = 54

Ответ: 54

Задача 13

Задача

Требуется выполнить деление: -18 :

Решение:

-18 : = -18 : = -18 : (-20 + 26) = -18 : 6 = -3

Ответ: -3

Задача 14

Задача

Нужно найти значение выражения:

(−1)−(−512)⋅(+411)=(−1)−(−521)⋅(+114)

Решение:

(−1)−(−512)⋅411=−1−(−112)⋅411=(−1)−(−521)⋅114=−1−(−211)⋅114=−1−(−2)=−1+2=1−1−(−2)=−1+2=1

Ответ: 1

Задача 15

Задача

Необходимо вычислить:

Вычислить |a| — |b| + |c|

при a = -8, b = -5, c = 1

Решение:

|-8| — |-5| + |1| = 8 — 5 + 1 = 4

Ответ: 4

Задача 16

Задача

Требуется решить пример:

:45=:54

Решение:

:45=:54=

:45=:54= (2,4−0,18−0,22):25=

2:45=52=2,5(2,4−0,18−0,22):52=2:54=25=2,5

Ответ: 2,5

Как правильно выполнять вычитание

1. Получение разности

Для выполнения вычитания следует следующая последовательность действий:

• Поставьте вычитаемое число под вычитающим так, чтобы разряды чисел были согласованы вертикально.
• Начиная с самого правого разряда, выполните вычитание цифр этой позиции. Если разряд вычитаемого числа меньше разряда вычитающего числа, возможно понадобится проведение заема.
• При проведении заема из следующего разряда, уменьшите его на единицу.
• Продолжайте вычитание по каждому разряду чисел, проводя заемы при необходимости.
• Результат будет числом с противоположным знаком от заемаемого числа, если оно было больше вычитающего, или с тем же знаком, если разность отрицательная.

2. Работа с отрицательными числами

Вычитание отрицательных чисел требует особого внимания. При вычитании отрицательного числа у нас получается сложение, где знаки одинаковы, а при вычитании из отрицательного числа, знаки отличаются.

Пример:

Вычитающее	Число	Разность
5	-3	5 + (-3) = 2
-2	-7	-2 – (-7) = -2 + 7 = 5

3. Примеры вычитания

Для наглядности рассмотрим несколько примеров вычитания:

• Пример 1: 67 – 23 = 44
• Пример 2: -42 – 15 = -57
• Пример 3: -32 – (-17) = -32 + 17 = -15
• Пример 4: 78 – (-43) = 78 + 43 = 121

Помните, что для успешного выполнения вычитания необходимо внимательно следить за знаками чисел, правильно согласовывать разряды и проводить заемы при необходимости. Практикуйтесь на различных примерах, чтобы научиться выполнять вычитание легко и безошибочно.

Вычитание отрицательных чисел и чисел с разными знаками

Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:

Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.

Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.

Определите, чему будет равно значение выражения: от -510 отнять +210.

На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:

-510-(+210)

Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:

Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.

Например: -5-(+2).

Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).

По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:

-5+(-2)=-(5+2)=-7

Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:

Запишем выражение:

-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:

-510-(+210)=-510+(-210)=-(510+210)=-720.

Вычисления окончены.

Рассмотрим следующее задание.

Найдите значение выражения: -248+248.

Используем правило сложения значений с разными знаками.

-248=|248|;

248=|248|;

248 – 248=0.

Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.

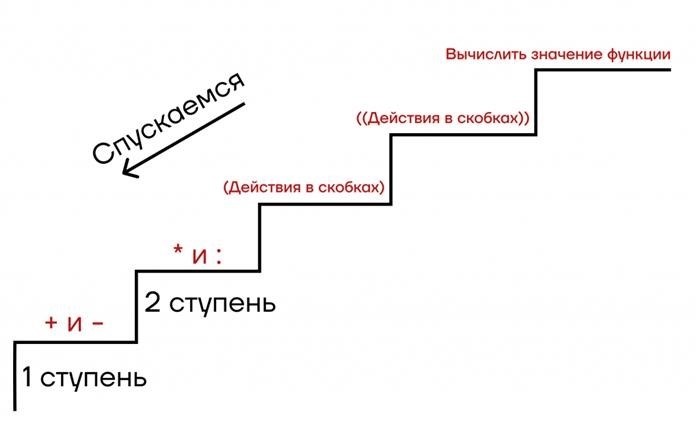
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.

К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

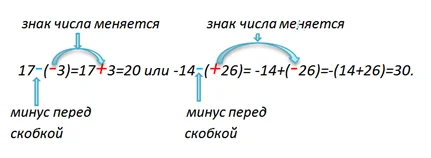
Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».

Вычисли: -36+(-7).

В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.

В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.

Минутка истории

История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.

Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом   .

Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.

Числовые множества

Ключевые слова: натуральные числа, разность, частное, числовое выражение, деление с остатком, простые и составные числа, разложение на простые множители, целые числа, рациональные числа, основное свойство дроби иррациональные числа, действительные числа

Числа вида N = {1, 2, 3, ….} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов

1. Если m, n, k — натуральные числа, то при m — n = k говорят, что m — уменьшаемое, n — вычитаемое, k — разность; при m : n = k говорят, что m — делимое, n — делитель, k — частное, число m называют также кратным числа n, а число n — делителем числа m, Если число m — кратное числа n, то существует натуральное число k, такое, что m = kn.
2. Из чисел с помощью знаков арифметических действий и скобок составляются числовые выражения. Если в числовом выражении выполнить указанные действия, соблюдая принятый порядок, то получиться число, которое называется значением выражения.
3. Порядок арифметических действий: сначала выполняются действия в скобках; внутри любых скобок сначала выполняют умножение и деление, а потом сложение и вычитание.
4. Если натуральное число m не делится на натуральное число n, т.е. не существует такого натурального числа k, что m = kn, то рассматривают деление с остатком: m = np + r, где m — делимое, n — делитель (m>n), p — частное, r — остаток.
5. Если число имеет только два делителя (само число и единица), то оно называется простым: если число имеет более двух делителей, то оно называется составным.
6. Любое составное натуральное число можно разложить на простые множители, и только одним способом. При разложении чисел на простые множители используют признаки делимости.
7. Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается D(a,b). Если числа a и b таковы, что D(a,b) = 1, то числа a и b называются взаимно простыми.
8. Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Оно обозначается K(a,b). Любое общее кратное чисел a и b делится на K(a,b).
9. Если числа a и b взаимно простые, т.е. D(a,b) = 1, то K(a,b) = ab .

Числа вида: Z = {… -3, -2, -1, 0, 1, 2, 3, ….} называются целыми числами, т.е. целые числа — это натуральные числа, числа, противоположные натуральным, и число 0.

Натуральные числа 1, 2, 3, 4, 5…. называют также положительными целыми числами. Числа -1, -2, -3, -4, -5, …,противоположные натуральным, называются отрицательными целыми числами.

Целые и дробные числа составляют множество рациональных чисел: Q = Z $$\cup$$ {$$\frac{m}{n}$$}, где m — целое число, а n — натуральное число.

1. Среди дробей, обозначающих данное рациональное число, имеется одна и
   только одна несократимая дробь.Для целых чисел — это дробь со
   знаменателем 1.
2. Каждое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби.
3. Дробь $$\frac{m}{n}$$ называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или раен ему.
4. Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.
5. Основное свойство дроби: если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получится дробь, равная данной.
6. Если числитель и знаменатель дроби взаимно простые числа, то дробь называется несократимой.
7. В виде десятичной дроби можно записать правильную дробь, знаменатель которой равен степени с основанием 10. Если к десятичной дроби приписать справа нуль или несколько нулей, то получится равная ей дробь. Если десятичная дробь оканчивается одним или несколькими нулями, то эти нули можно отбросить — получиться равная ей дробь. Значимыми цифрами числа называются все его цифры, кроме нулей, стоящих в начале.
8. Последовательно повторяющаяся группа цифр после запятой в десятичной записи числа называется периодом, а бесконечная десятичная дробь, имеющая такой период в своей записи, называется периодической. Если период начинается сразу после запятой, то дробь называется чистой периодической; если же между запятой м периодом есть другие десятичные знаки, то дробь называется смешанной периодической.

Числа не являющиеся целыми или дробными называются иррациональными.

Каждое иррациональное число представляется в виде непереодической бесконечной десятичной дробью

Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел: рациональных и иррациональных

См. также:Дроби, Десятичные числа

Определение целых, рациональных, вещественных и комплексных чисел

Определение целых чисел

Определение:

Множество целых чисел (англ. integers) определяется как замыкание множества натуральных чисел относительно арифметических операций сложения и вычитания .

Таким образом, сумма, разность и произведение двух целых чисел есть снова целые числа. Оно состоит из натуральных чисел , чисел вида -n () и числа ноль.

Необходимость рассмотрения целых чисел продиктована невозможностью (в общем случае) вычесть из одного натурального числа другое. Целые числа являются кольцом относительно операций сложения и умножения.

Отрицательные числа ввели в математический обиход Михаэль Штифель (1487—1567) в книге «Полная арифметика» (1544), и Никола Шюке (1445—1500).

Определение рациональных чисел

Определение:

Множество рациональных чисел (англ. rational numbers) обозначается и может быть записано в виде:

Нужно понимать, что численно равные дроби такие как, например, и , входят в это множество как одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

Здесь — наибольший общий делитель чисел и .

Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа знаменатель , то является целым числом. В этой связи возникают некоторые обманчивые предположения. Однако, хотя кажется, что рациональных чисел больше чем целых, и тех и других счётное число (то есть оба они могут быть перенумерованы натуральными числами, причём явно).

Определение вещественных чисел

Oсновная статья: Вещественные числа

Определение:

Веще́ственное число (англ. real number) — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений.

С точки зрения современной математики, множество вещественных чисел — суть, непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.

Множество вещественных чисел имеет стандартное обозначение — R (полужирное «R»), или (blackboard bold «R») от realis — действительный.

Определение комплексных чисел

Определение:

Ко́мпле́ксные чи́сла (англ. complex number) — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и  — вещественные числа,  — мнимая единица (одно из решений уравнения ).

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях.

Координатная прямая

Давайте внимательно рассмотрим шкалу термометра и постараемся схематично её изобразить. Шкала является прямой линией. Чертим её:

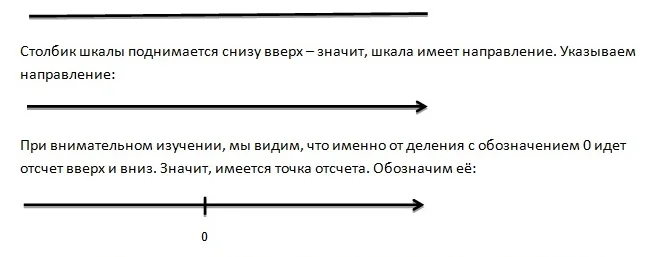
Замечаем, что каждое деление соответствует 1 градусу. Выходит, шкала имеет единичный отрезок.

Выбираем на нашем рисунке единичный отрезок не забывая, отложить его в обе стороны от начала отсчета:

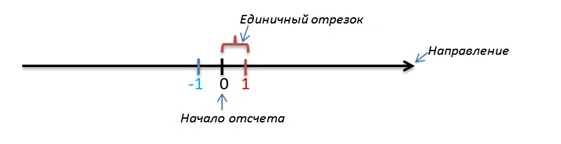
Посмотрим на полученное изображение. Построенная геометрическая фигура имеет направление, точку начала отсчета и единичный отрезок. В математике, такие фигуры имеют свое название – координатная прямая.

Важным моментом, является то, что на координатной прямой по правую сторону от точки начала отсчета (0) находятся положительные числа, а по левой стороне – отрицательные (записанные со знаком «минус»).

Мы изобразили координатную прямую, отметили на ней числа от -7 до 7.

На самом деле, на рисунке изображен небольшой фрагмент прямой. Данная линия  продолжается в обе стороны до бесконечности, так как по определению, она не имеет ни начала, ни конца.

Как вычитать числа с разными знаками

Правило сложения чисел с противоположными знаками:

Для сложения положительного и отрицательного числа необходимо:

1. вычислить модули чисел;

2. выполнить сравнение полученных чисел:

   • если они равны, то исходные числа являются противоположными и их сумма равна нулю;
   • если они не равны, то нужно запомнить знак числа, у которого модуль больше;

3. из большего модуля вычесть меньший;

4. перед полученным значением поставить знак того числа, у которого модуль больше.

Сложение чисел с противоположными знаками сводится к вычитанию из большего положительного числа меньшего отрицательного числа.

Правило сложения чисел с противоположными знаками выполняется для целых, рациональных и действительных чисел.

Пример 3

Сложить числа $4$ и $−8$.

Решение.

Требуется выполнить сложение чисел с противоположными знаками. Воспользуемся соответствующим правилом сложения.

Найдем модули данных чисел:

$|4|=4$;

$|-8|=8$.

Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.

Далее от большего модуля отнимем меньший модуль, получим:

$8−4=4$.

Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$

Краткая запись решения:

$4+(–8) = –(8–4) = –4$.

Ответ: $4+(−8)=−4$.

Для сложения рациональных чисел с противоположными знаками их удобно представить в виде обыкновенных или десятичных дробей.

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

«Минус пять меньше, чем три»

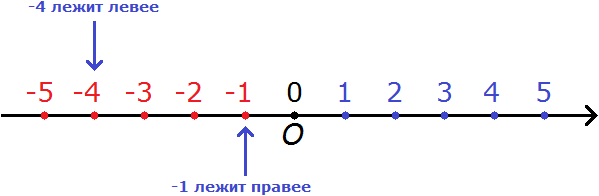
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

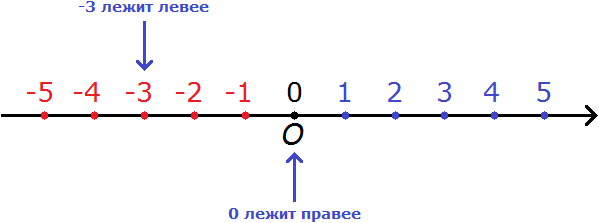
Правило 3. Ноль больше любого отрицательного числа.

Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

Ноль больше, чем минус три

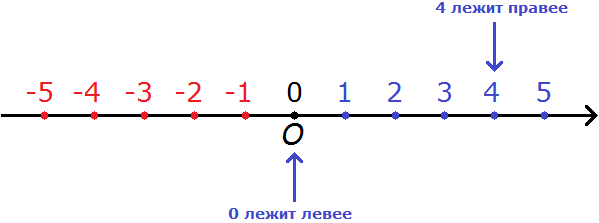
Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Сравнение положительных и отрицательных чисел

Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.

Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех. Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.

На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:

−5 < 3

Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.

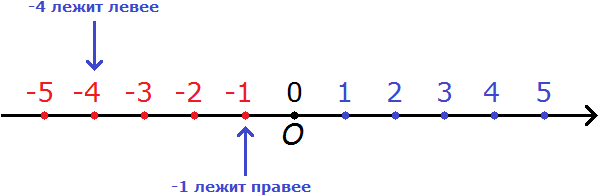
Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:

-4 < -1

Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.

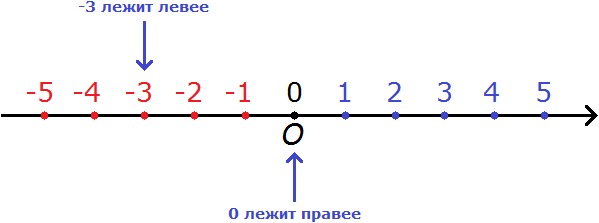
При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:

0 > -3

Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.

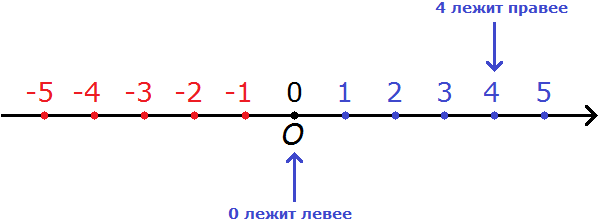
На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:

0 < 4

Рациональные числа в Python

Рассмотрим примеры рациональных чисел и их свойств на языке Python. В питоне есть специальный модуль fractions, который позволяет нам работать с рациональными числами, а в нём класс Fraction, являющийся реализацией дробного значения.

Ну что ж, за дело. Для начала импортируем класс Fraction из модуля fractions, чтобы мы могли им пользоваться:

Теперь разберём, как работает этот класс. При создании объекта Fraction в конструктор можно передать:

• два значения, где первое — это числитель, а второе — знаменатель (переменная a);
• дробное значение в виде строки (переменная b);
• вещественное значение (переменная c);
• другой Fraction, так как Fraction и является реализацией рационального дробного значения (переменная d).

Видно, что значение переменных Fraction при выводе показывает дробный вид рационального числа 0,5, а во второй строке вывода при приведении значения ½ к float, получим его вещественное представление.

Поменяем значения переменных и пройдёмся по свойствам рациональных чисел, взяв отрицательную дробь -¾, дробь ⅔ (с бесконечным периодом) и целое число 10:

Возьмём сочетательное свойство сложения и применим формулу (a + b) + c = a + (b + c), дабы убедиться, что значения будут равны, а также приведём вид дробей к float:

Как можно заметить, значения одинаковые, а при выводе в вещественном виде у нас получается число с бесконечным периодом 6. А как мы уже говорили выше, такие числа также относятся к рациональным.

Проделаем ту же операцию по формуле распределительного свойства умножения:

Значения получились равные, но можно заметить, что при приведении к вещественному виду период рационального числа нарушается — 3 в конце заменяется на 4. Это происходит в силу особенностей вычислений в языке Python. Если мы на листе бумаги разделим 5 на 6, то получим 0,8333…, где 3 будет повторяться до бесконечности.

И напоследок разберём случай с делением рациональных чисел с использованием переместительного свойства. Для начала разделим a на b. Теперь поменяем операнды местами и посмотрим, что получится. Для этого умножаем a на дробь 1/b, подставив в качестве второго операнда класс Fraction, который и реализует эту дробь. Вуаля:

Действия с числами разных знаков: Подведение итога

Когда мы складываем два числа с разными знаками, результат может быть положительным или отрицательным в зависимости от величины чисел и их знаков. Если слагаемые числа имеют противоположные знаки, мы вычитаем из большего числа по модулю меньшее число и приписываем знак числу с большим по модулю значением. Если же слагаемые числа имеют одинаковые знаки, мы складываем их по модулю и приписываем результату этот же знак.

Вычитание чисел с противоположными знаками можно свести к сложению, меняя знаки слагаемых чисел и выполняя сложение. Таким образом, действия с числами разных знаков довольно просты и интуитивно понятны.

Важно помнить, что при выполнении этих действий нужно учитывать знаки чисел и правильно определять результат. Использование математических правил и понимание сути операций помогут успешно выполнять сложение и вычитание чисел с разными знаками

В специальных случаях, например при работе с отрицательными координатами или финансовыми данными, знание и понимание операций с числами разных знаков может быть особенно полезным.