Устный счет: техника быстрого счета в уме

Когда можно решать примеры в пределах 20

При полном усвоении навыков счета до 10 рекомендуют приступить к действиям на втором десятке. Здесь необходимо только понимание, без подсказки и списывания у соседа. Как научить считать и разъяснять примеры ребенку в пределах 20?  Следует придерживаться пошаговой методики:

1. Выучить порядковый счет второго десятка, очередность каждого элемента числового ряда. Для облегчения запоминания используют одинаковые предметы – карточки, кубики. Нанести числа только на первые десять единиц. Разложить их рядами, первый десяток с подписями, под ним второй, «слепой».
2. Запоминать по схеме 14 – к слову четыре добавляется «– надцать», и так с каждым новым термином. Ребенок должен усвоить смысл названия порядковых чисел от 11 до двадцати.
3. Приступить к понятию первый десяток, потом добавлять элементы второго ряда и проговаривать действия. «Десять плюс четыре получится четырнадцать». Должны прозвучать так все данные в интервале второго десятка.
4. Отработать действия со сложением без перехода. По типу 10 + 6 = 16; 16 – 6 = 10. Когда этот этап освоен, выполняют действия повышенной сложности.

Пазлы для счета до 20

Примеры с переходом через десяток требуют развивать навыки устного счета. Знание состава числа при равной сумме облегчают запоминание алгоритма расчета по действиям на сложение и вычитание в пределах 100.

Свойства сложения и вычитания натуральных чисел

При решении задач на сложение и вычитание натуральных чисел важно грамотно использовать свойства этих действий. К ним относятся:

К ним относятся:

1. Переместительное свойство.

Для понимания рассмотрим пример. На ветке сидело 5 воробьев. К ним прилетело еще трое. Сколько воробьев в результате сидит на ветке? Произведя действие по сложению, получаем:

5+3=8

Данную задачу можно сформулировать и по другому, а именно: На ветке сидело трое воробьев. К ним прилетело еще пятеро. Сколько всего воробьев? Теперь прибавляем к трем пять. В результате — та же сумма. 8.

Следовательно, можно поменять местами слагаемые, от чего сумма не изменится. Данное свойство формулируется следующим образом: от перемены мест слагаемых сумма не меняется.

Переместительное свойство можно использовать для облегчения устного счета. Так, если к 9 нужно добавить 23, это устно сделать затруднительно. Гораздо проще представить действие, когда к 23 прибавить 9. В итоге сумма равна 32.

Переместительное свойство справедливо только для сложения. В вычитании оно не работает.

2. Сочетательное свойство.

Упростить сложение с помощью сочетательного свойства также легко. Если к имеющемуся числу нужно добавить сумму двух чисел, то можно выбрать, какое из них прибавлять первым. В таком случае действие рассматривается как нахождение суммы первого числа с одним из пары добавляемых чисел, с последующим прибавлением второго.

Рассмотрим на примере.

Если к 7 нужно прибавить сумму 15 и 23, то можно на первом этапе прибавить 23, а после, получив 30, прибавить к нему 15. Запишем пот действиям:

7+(15+23)=(7+23)+15=30+15=45

В математических примерах на сложение одним из слагаемых может быть 0. В таком случае сумма будет равна первому слагаемому. Другими словами, ноль не увеличивает число при сложении с ним.

Определенные законы существуют и для вычитания. Основные из них следующие:

1. Если уменьшаемое и вычитаемое представлены одинаковыми числами, то их разность будет равна нулю. Наглядно это становится понятным на координатном луче. Отступив от начала координат 7 единиц, а потом, вернувшись на эти семь делений назад, получаем ноль.
2. Аналогично третьему свойству сложения в примере на вычитание в качество вычитаемого может присутствовать ноль. Так, если от 9 нужно вычесть ноль, разность будет равна уменьшаемому, т.е. 9.
3. Данное свойство также аналогично одному из свойств сложения. Если в задании требуется из числа вычесть сумму чисел, то можно выбрать и одно из них вычесть первым. Например, 16-(6+3)=(16-6)+3=10+3=13. Решение таким способом гораздо легче.
4. Выбирать первостепенное действие можно и при вычитании числа из суммы. Например, (16+25)-6=(16-6)+25=10+25=35. Такое перемещение членов математического действия гораздо облегчает задачу и сокращает время на ее решение.

Приведенные свойства можно выразить в виде формул:

Вычитание натуральных чисел

Аналогично сложению выполняется вычитание — действие, которое заключается в уменьшении первого числа на величину второго. При этом первое называется уменьшаемым, второе — вычитаемым, а полученный результат — разностью.

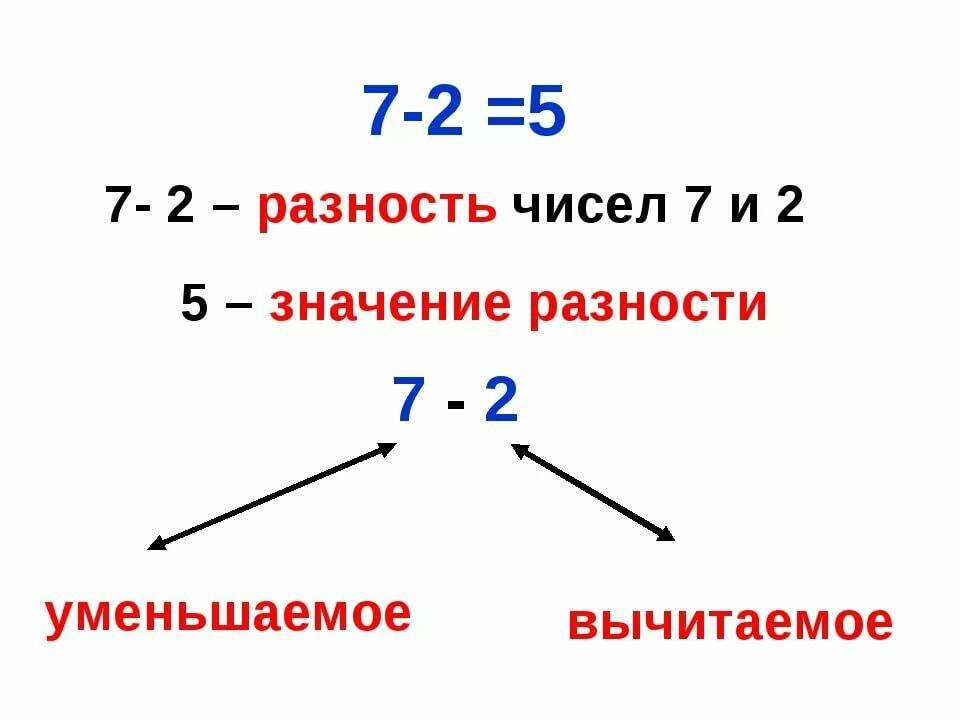
Рассмотрим действие вычитания на схеме с лучами.

На первом луче от имеющегося числа 7 необходимо вычесть 3. Сделав поочередно три шага влево по лучу, можно определить разность в этом действии. Она равна четырем.

На втором координатном луче аналогично произведено действие вычитания из шести четыре. Разность — два.

Умение вычесть из одного числа другое пригодится в решении задач по нахождению одного из слагаемых при известной сумме. Так, например, зная, что сумма двух чисел равна 7, а один из слагаемых трем, можно найти второе слагаемое. Для этого производим действие вычитания:

7-3=4

Разность в данном примере составляет 4.

Действие по вычитанию натуральных чисел может происходить в том случае, когда вычитаемое меньше уменьшаемого. В противном случае в результате получится отрицательное число, которое не является натуральным.

Как объяснить связь сложения и вычитания

Для лучшего восприятия следует научить малыша составу. Методика заключается в трех шагах:

1. На привычных предметах усвоить, что одно из слагаемых может меняться в сторону уменьшения, другое возрасти при одинаковой сумме. Удачным пособием станут упаковки для яиц (по 10); боксы для печенья (по 6,8 или 12), календарные дни (по 7).
2. Следует проследить, чтобы ребенок сделал записи в тетради по возможным комбинациям числительных.
3. Вместе с учеником подготовить карточки с надписями: 6 + 3 = 9; 4 + 5 = 9; 2 + 7 = 9; 1 + 8 = 9. Лучше распределить каждый пример на отдельную карточку.

Теперь нужно приложить усилия к запоминанию. Ребенок должен наизусть, не считая, запомнить все возможные комбинации слагаемых, дающих одну сумму. Не нужны длинные занятия. Успех придет быстрее, когда урок на запоминание будет быстрым, как перерыв между лепкой или рисованием.

Связь между сложением и вычитанием

Если ребенок все запомнил и не пытается «посчитать», можно приступать к следующему шагу. При замене знакомых карточек новыми, малыш должен писать сразу ответы. Приступаем к самому сложному – вычитать, используя знание составляющих. Вначале необходимо повторить карточки с действиями. Потом нужно спросить у ребенка, что будет с результатом, если убрать одно из слагаемых.

Данная цепочка поможет оценить связь сложения с вычитанием методом запоминания. Ученик должен понять, что вспомнить знакомое сочетание легче, чем считать в уме. В дальнейшем принцип поможет легче освоить решение линейных уравнений.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

Раньше все считали без калькуляторов

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Учимся решать примеры до 10

Для того чтобы выучиться верно и мгновенно считать, нужно постоянно решать примеры. Для высчитывания и запоминания на начальных этапах следует сделать акцент на мышлении ребенка на основе наглядных образов. Здесь возникает проблема: дети часто не воспринимают математические понятия. Решением станут практические действия с жизненными примерами.

Учимся считать

Учителя используют три основных метода для обучения счету:

1. На принципе знания числового состава
2. Запоминать наизусть таблицы действий, включая деление и умножение.
3. Использовать спец.приемы для получения результата.

Рассмотрим все методики по порядку.

Примеры на вычитание с картинками

Принцип знания состава

Подготовка должна начинаться с изучения азов математики. Рассказывая ребенку, нужно объяснять, что каждое число это группа с заданным количеством элементов.

Состав числа для запоминания

Важно! Мало сосчитать до пяти. Убедитесь, что вы предлагаете показать пять пальцев, положить на стол пять конфет или изобразить на листке пять кругов

Необходимо связать число и сказочных героев или другие знакомые для ученика предметы:

1. Одна репка.
2. Две стороны у монетки.
3. Три медведя.
4. Четыре стороны света.
5. Пять пальцев на ручке малыша.

Ребенка важно приучать к картинке, соединенной со всеми элементами. Необходимо играть в математическое домино

Для этого нужно взять десять кубиков с размером ребра 1,5-2 см, стоящих в коробке. Подойдут и детали конструктора Лего. Если нет подходящих предметов, то можно распечатать другие пособия.

Исходя из знания состава, ребенок может решить, складывать ему или вычитать. Например, чтобы ответить, сколько будет «шесть плюс три», он должен знать, что 6 и 3 равняются 9. А «семь минус два» получится пять, потому что 7 это 2 и 5.

Пособие для изучения состава

Запоминания таблиц наизусть

Есть большое количество приемов приучить ребенка сразу запомнить таблицы. Почти половина примеров на сложение и вычитание бессознательно заучиваются детьми по окончании ознакомления с законом перемещения.

Можно брать стихи, подпевки. Самым популярным образцом служит строка песни «Дважды два четыре, это всем известно в целом мире». Отличную информацию находят, познакомившись с методикой Николая Зайцева, программой «Песнезнайка».

Для закрепления знания табличных данных, можно предложить детям работать с:

• раскрасками;
• компьютерными играми по математике;
• мультимедийными презентациями.

Умение прибавлять в тестах со звездочкой поможет потом учить сложный материал.

Домашние упражнения

Использование вычислительных приемов

Наивысший уровень результата устного счета – это способность нахождения самого быстрого и удобного метода для подсчета итога. Так, например, одним из легких способов обучить школьника считать на занятиях является техника присчитывания и «перепрыгивания». Дети быстро усваивают, что при добавлении 1 получается последующее значение, а при уменьшении на 1 получается предыдущее. После этого можно узнать о лучшем напарнике числа 2 – кузнечике, который умеет перескочить цифру и вызвать результат сложения или вычитания 2.

Принципы и правила вычитания

Вычитание является одной из основных операций в математике. Она позволяет находить разность между двумя числами.

Основные правила вычитания:

1. Первое число, из которого вычитают, называется уменьшаемым, а второе число — вычитаемым.
2. Вычитаемое вычитается из уменьшаемого.
3. Результат вычитания называется разностью.

Пример вычитания:

		3	9
—		1	2
		2	7

В этом примере уменьшаемое число равно 39, а вычитаемое число равно 12. После вычитания получаем разность, равную 27.

Существуют различные способы вычитания, такие как вычитание в уме, вычитание с переносом и др. Каждый метод имеет свои особенности и может быть использован в разных ситуациях.

Интересные способы научить прибавлять и отнимать

Ребенок должен запомнить многие числовые комбинации. Чтобы помочь лучше понять этот материал, рекомендуется предложить ему следующие задачи:

• Рассортировать данное количество объектов в три тарелки, создав разные комбинации (варианты разные: повесить игрушки на две елки, расставить цветы в двух вазах, разместить гномов в двух домах);
• дополнить число до желаемого;
• заполнить ячейки, в которых записан состав с присвоенным номером;
• дорисовать домино.

Числовой ряд

Поможет усвоить устный счет игра в интервал между значениями. Мама говорит, что загадала определенное число в промежутке от 5 до 18. Ребенок должен угадать, если он ошибается, взрослый определяет место в ряду, регулируя поиски словами «больше», «меньше», «добавь один», «отними два».

Первые успехи

Ребенку будет сложно понять на уроках математику в первом классе, если он не усвоил технику счета. Терпение, игровые методы, непринужденность и регулярность упражнений это необходимые условия для успешного обучения. Даже одна десятая материала, усвоенного ребенком самостоятельно, поможет освоить школьную программу.

Законы сложения натуральных чисел

Зная особенности натурального ряда, можно выполнить задание по определению неизвестного числа. Например, числом, следующим за тройкой, является четыре, а следующим за числом 25, является 26.

Используя такое свойство, можно складывать два натуральных числа. Так, если нужно к трем прибавить два, значит, следует передвинуться на два шага вправо. Получится пять.

Аналогичный способ приемлем для сложения чисел, которые могут быть разложены на небольшое количество единиц. Для иных случаев он очень не удобен. Увеличение числа поединично занимает много времени.

Вторым вариантом сложения является определение суммы единиц, которые составляют оба числа.

Если необходимо сложить два числа, они превращаются в слагаемые. Их может быть несколько. Последовательность сложения может быть различной, но в результате обязательно получается число, которое в математике называется суммой.  

Из данного действие вытекает определение математического действия.

Математическое действие — способ нахождения нового числа с использованием двух или нескольких имеющихся.

При этом не только сложение является математическим действием. Ведь не всегда требуется найти число в результате прибавления к нему другого числа. Задача может заключаться в уменьшении имеющегося на определенную величину.

Публикация «Конспект занятия в старшей группе „Сложение и вычитание“» размещена в разделах

• Конспекты занятий. Все конспекты
• Сложение и вычитание. Знаки «плюс» и «минус»
• Старшая группа
• Темочки

3) развивать внимание, память,речь, воображение, навыки самоконтроля, мелкую моторику рук;

4) воспитывать желание выполнять действия, идти к поставленной цели, начатое дело доводить до конца.

Предварительная работа,закрепить счёт до 10, свойства фигур, работа в учебнике – тетради «Игралочка – ступенька к школе»,ч. 3.

Материалы и оборудования: игрушка Зайка, карточки «плюс и минус», 3 больших зелёных квадрата и 2 маленьких синих квадрата, счетный материал: на каждого ребенка по 5 яблок и один ежик.

Что такое натуральные числа

Много ситуаций вокруг нас связано с действиями с натуральными числами. Каждое из них можно представить шагами на обычной школьной линейке с нанесенными делениями, числовой прямой и координатном луче. В результате сложения исходное натуральное число увеличивается, а в результате вычитания — уменьшается. Для таких математических действий также существуют законы, которые будут рассмотрены ниже.

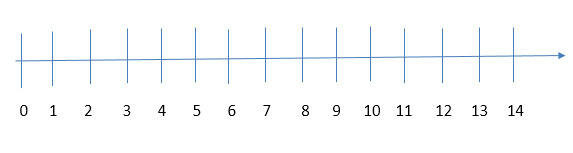
Понятие натурального числа обусловлено необходимостью естественного счета предметов и расположения цифр друг относительно друга. Множество таких чисел характеризуется бесконечностью. На деле это выглядит так: относительно любого числа есть еще одно, которое на единицу больше. Если расположить эти числа в порядке возрастания, получится натуральный ряд – еще одно математическое понятие, связанное с натуральными числами. Примером такого ряда является обычная линейка. В то же время необходимо понимать, что линейка имеет последнее число (например, линейка на 30 см ограничивается числом 30, а на 40 см — 40). В отличие от обычной линейки, числовая прямая не имеет крайнего числа, как показано на рисунке:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Представляя натуральные числа в виде числовой прямой, необходимо также помнить, что натуральным рядом является только множество целых чисел, причем имеющих знак «+». Если на прямой нанесены числа, расположенные слева от нуля, то этот ряд не является натуральным. Поэтому в математике говорят о расположении натуральных чисел на луче.

Расположение чисел на луче помогает представить действия с натуральными числами:

• продвинувшись на несколько делений вправо, число получает увеличение на число таких шагов;
• если переместиться на несколько шагов влево, получается результат, равный действию вычитания из исходного числа количества геометрических шагов.

Примечание 1

Геометрическим шагом называется единица, на которую совершается геометрическое действие.

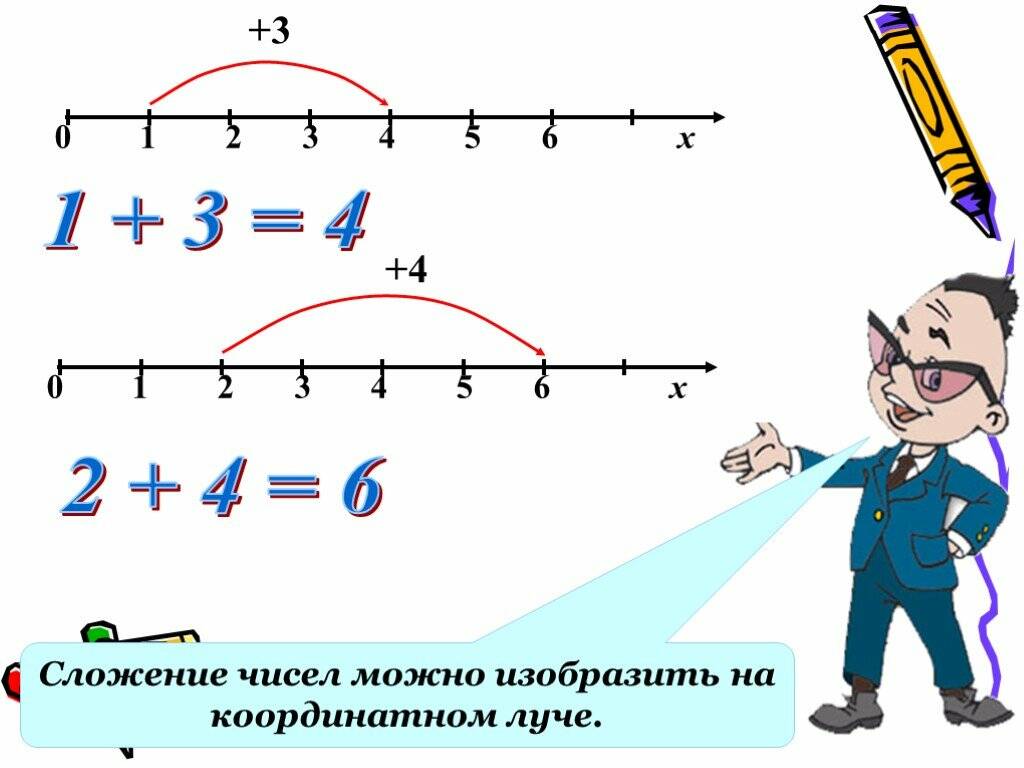
На данном рисунке шагом является любой отрезок между двумя соседними натуральными числами.

Все натуральные числа можно назвать их множеством. Для обозначения такого множества определена буква латинского алфавита N.

В математике для множества натуральных чисел существуют следующие правила:

1. Единица является наименьшим натуральным числом.
2. При фоне существования наименьшего числа отсутствует наибольшее.
3. При сравнении каждого последующего числа с предыдущим, обязательное условие — их разница на единицу. Другими словами, каждый последующий участник ряда больше предыдущего на один.

Сложение и вычитание целых чисел

Сложение и вычитание целых чисел означает перемещение вправо или влево на числовой прямой. Чтобы прибавить целое число, переместитесь на соответствующее количество шагов вправо (для положительных целых чисел) или влево (для отрицательных целых чисел) на числовой прямой. Чтобы вычесть целое число, добавьте противоположное целое число. Целые числа называются противоположными, если они имеют одинаковое абсолютное значение, но разный знак. Например, 4 и -4, 12 и -12, 1 и -1.

Сложение положительных чисел

Сложение положительных чисел — это простая операция сложения. Например, прибавление 3 означает, что вам нужно сделать 3 шага вдоль числовой прямой в положительном направлении (вправо). Прибавление 14 означает, что вам нужно сделать 14 шагов в положительном направлении, и так далее. Некоторые примеры сложения целых положительных чисел показаны ниже:

0 + 3 = 3

4 + 3 = 7

-1 + 12 = 11

-5 + 1 = -4

Вычитание положительных чисел

Вычитание положительных чисел — это простая операция вычитания. Чтобы вычесть положительное число, переместитесь на соответствующее количество шагов в отрицательном направлении (влево) вдоль числовой прямой. Примеры вычитания целых положительных чисел показаны ниже:

0 — 1 = -1

12 — 9 = 3

44 — 46 = -2

-5 — 5 = -10

Сложение отрицательных чисел

Отрицательные числа представляют собой движение в отрицательном направлении (влево) на числовой прямой. Это означает, что прибавление отрицательного числа будет выполняться путем перемещения вдоль числовой линии влево:

5 + (-2) = 3

14 + (-12) = 2

-2 + (-13) = -15

Поскольку прибавление отрицательного числа выполняется путем перемещения вдоль числовой прямой в отрицательном направлении, эта операция эквивалентна вычитанию положительного числа:

3 + (-3) = 3 — 3 = 0

Вычитание отрицательных чисел

Чтобы вычесть отрицательное число, прибавьте к нему противоположное число. Это означает, что вычитание отрицательного числа равносильно прибавлению соответствующего положительного числа. Например:

-4 — (-11) = -4 + 11 = 7

Правила сложения и вычитания целых чисел

Правила сложения и вычитания целых чисел можно сформулировать следующим образом:

• Два одинаковых знака (+ + или — — ) дают положительный знак, +.
• Два противоположных знака (+ — или — +) дают отрицательный знак, -.

Приоритет операций в математике

Операции в математике выполняются по определенному порядку приоритета. Это помогает решать сложные математические выражения и получать правильные результаты.

Вот порядок приоритета операций, который следует помнить:

1. Скобки: вычисления в скобках всегда выполняются первыми.
2. Умножение и деление: умножение и деление выполняются перед сложением и вычитанием.
3. Сложение и вычитание: сложение и вычитание выполняются в последнюю очередь.

Если в выражении есть несколько операций с одинаковым приоритетом, то они выполняются слева направо.

Давайте рассмотрим пример:

Выражение	Результат
2 + 3 * 4	14
(2 + 3) * 4	20
10 / 2 — 3	2

В первом примере, сначала выполняется умножение, а затем сложение: 3 * 4 = 12, 2 + 12 = 14.

Во втором примере, сначала выполняется сложение в скобках, а затем умножение: 2 + 3 = 5, 5 * 4 = 20.

В третьем примере, сначала выполняется деление, а затем вычитание: 10 / 2 = 5, 5 — 3 = 2.

При использовании операций в математике важно помнить и следовать порядку приоритетов, чтобы получить правильные результаты

Указания по использованию

Чтобы использовать калькулятор для сложения и вычитания целых и десятичных чисел, введите заданное уравнение и нажмите «Вычислить». Калькулятор вернет окончательный ответ, а также пошаговый алгоритм решения с указанием конечного знака для каждой операции.
Поле ввода принимает следующие символы:

• Целые числа, например, 3, 6, 144, -15.
• Десятичные числа, где целая часть числа и десятичная часть разделены десятичной точкой (или запятой). Например, 3,0 , 8,978 , 123,901 , -12,36.
• Знак операции сложения +.
• Знак операции вычитания -.
• Скобки, (). Скобки, или круглые скобки, всегда должны идти парами, то есть уравнение должно содержать как открывающую, так и закрывающую скобку. Например, 3 + (-4), -98 — (-5,67). Вы не можете ввести 5 + (-3, так как это уравнение содержит только одну скобку. Символы, заключенные в скобки, всегда должны заканчиваться числом, а не знаком операции. Например, (3 — 4 + 5) является допустимым вводом, а (3 — 4 +) 5 — нет. Можно также использовать квадратные скобки, [], или фигурные скобки, {}, но калькулятор автоматически преобразует их в круглые скобки, ().

Вы можете использовать столько последовательных знаков операций, сколько необходимо, не разделяя их пробелами или другими символами. Для каждой операции калькулятор определит и продемонстрирует последний знак операции. Ниже приведены примеры правильного ввода:

• -33 + 15 — 1- — 2 (равно -17)
• (-33) + 15 — 1 — (-2) (равно -17)
• (-33 + 15 -1) — — 2 (равно -17)
• -33 + 15 — 1- — — — — — + 2 (равно -21)

Поле ввода принимает до 60 символов.

Чтобы очистить поле ввода, нажмите «Очистить».