Площадь и ее измерение
С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:
Sкв = a2, Sпр = а ∙ в. Единицей измерения площади является квадратный метр (м2).
Для измерения малых площадей применяются см2 и мм2, а большие площади – в км2. В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м2, 1 а = 100 м2.
Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR2. (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).
Арена цирка. () Круглый стол. () Спил дерева. ()
А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.
()
Существует правило нахождения площади тел произвольной формы:
- Разбить всю поверхность на равные квадраты с известной площадью.
- Подсчитать количество целых квадратов.
- Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
- Сложить результаты пунктов 2 и 3.
- Умножить площадь одного квадрата на общее число целых квадратов.
Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.
()
Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.
Измерение объема. Мензурка
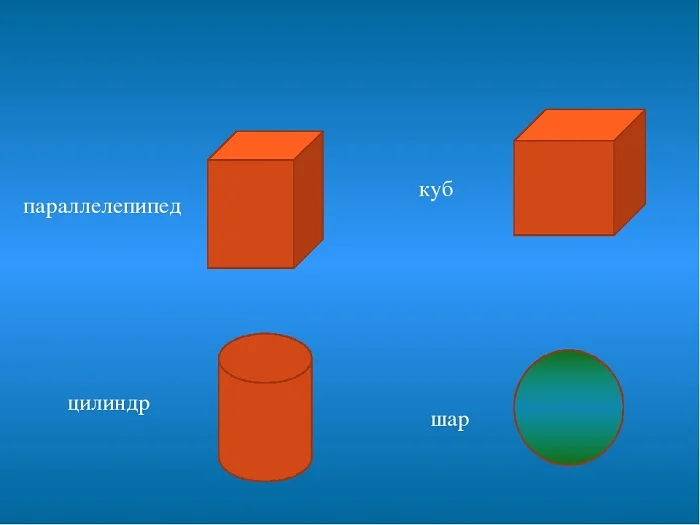
При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.
 (Источник)
(Источник)
Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:
Vпар = а ∙ в ∙ с (произведение длины, ширины и высоты),
Vк = а3 (а — ребро куба),
Vцил = π ∙ r2 ∙ h (r — радиус основания, h – высота цилиндра),
Vш = 4/3 π ∙ R3 (R – радиус шара).
О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями. При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.
 (Источник)
(Источник)
На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см3 = 10-6 м3.
Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.
 (Источник)
(Источник)
Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити
Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела
Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.
Физические величины
Такие величины, как масса, длина, время…. и т. д. называются физическими величинами, и нам необходимо точно измерять их в повседневной жизни. Физические величины можно разделить на фундаментальные физические величины и производные физические величины.
Фундаментальные физические величины — это физические величины, которые не могут быть определены в терминах других физических величин, таких как длина, время и масса, длина (L) определяется сама по себе, никакие другие физические величины не требуются для определения длины, длина линейка = 20 см.
Производные физические величины — это физические величины, которые могут быть определены в терминах фундаментальных физических величин, таких как объем, скорость и ускорение. Объем вычисляется из длины, Объем кубоида = длина × ширина × высота.
Физические величины — это сокращенная формула, которая дает физическую иллюстрацию конкретного показания. Связь между физическими величинами может быть выражена математическими уравнениями, которые являются сокращенной иллюстрацией конкретного показания (Физический смысл).
Например: когда движущееся тело преодолевает расстояние (d) за время (t), его скорость (v) может быть выражена как: Скорость = смещение / время, V = d / t. Это соотношение называется физико-математическим уравнением.
Объем тела, его измерение.
Объем– это положительная скалярная величина, характеризующая размер геометрического тела.
Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:
1. равные тела имеют равные объемы;2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.
Будем объем тела Q обозначать V(Q).Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е3. Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е3, которое называют численным значением объема при данной единице объема.Свойства численных значений объема1. Если тела равны, то равны и численные значения их объемов:
Q1 = Q2
Для измерения объемов площадей используют стандартные единицы площади: м3, дм3, см3, мм3. Основная единица измерения объема – кубический метр. Соотношения между единицами объема: 10-9 км3 = 1м3 = 103дм3 = 106 см3 = 109 мм3. В начальной школе рассматривается объем прямоугольного параллелепипеда. Рассмотрим случай, когда длина, ширина и высота выражены натуральными числами. Если стороны основания равны а и b, то на это основание можно уложить а ∙ b единичных кубиков. Так как в высоту укладывается с таких слоев, то объем параллелепипеда вычисляется по формуле V = а ∙ b∙ с. Таким образом объем прямоугольного параллелепипеда равен произведению трех его измерений. В начальной школе изучается также такая величина, как емкость. Она рассматривается как объем сыпучих и жидких тел. Единица измерения емкости – литр. 1 л = 1 дм3. Измерить объемы тел более трудно, чем площадь фигур. Приведем несколько способов измерения объемов. 1. Правило Архимеда. Объем воды, вытесненной телом при погружении, равен объему этого тела. 2. Косвенный способ измерения объема. · Посредством измерения длин сторон и других отрезков и нахождения площади с помощью формул. · Нахождение объем через массу и плотность тела. 3. Метод дополнения (разбиения).
4. Объем (емкость) сосудов – с помощью наполнения.
Масса, ее измерения.
Определение. Массой тела называется положительная величина, определенная для каждой фигуры так, что: 1) масса одинакова у тел, уравновешивающих друг друга на весах; 2) масса складывается, когда тела соединяются вместе: масса нескольких тел, взятых вместе, равна сумме их масс. Измерение массы производится с помощью весов. Выбираем тело е, масса которого принимается за единицу. Предполагается, что можно взять и доли этой массы. Например, если за единицу массы взят килограмм, то в процессе измерения можно использовать и такую его долю, как грамм: 1 г = 1/1000 кг. На одну чашку весов кладут тело, массу которого измеряют, а на другую – тела, выбранные в качестве единицы массы, т.е. гири. Этих гирь должно быть столько, чтобы они уравновесили первую чашку весов. В результате взвешивания получается численное значение массы данного тела при выбранной единице массы. Это значение приближенное. Например, если масса тела равна 5 кг 350 г, то число 5350 следует рассматривать как приближенное значение массы данного тела (при единице массы – грамм). Для численных значение массы справедливы все утверждения, сформулированные для длины, т.е. сравнение масс, действия над ними сводятся к сравнению и действиям над числовыми значениями масс (при одной и той же единице массы). Основная единица массы – килограмм. Из этой основной единицы образуются другие единицы массы: грамм, тонна и др.
Источник
Измерение коротких отрезков с помощью штангенциркуля
Штангенциркуль имеет две губки (каждая прикреплена к шкале), которые представляют собой фиксированную шкалу (одно деление = мм), и скользящую (нониусную) шкалу, которая может скользить по фиксированной шкале и делиться на несколько делений (одно деление = 0,99 мм), деление на нониусной шкале меньше деления на фиксированной шкале на 0,01 мм.
Предмет помещают между двумя губками штангенциркуля и осторожно нажимают, показание фиксированной шкалы записывается непосредственно перед тем, как выравнивается нулевая отметка скользящей шкалы. Вам нужно найти отметку на нониусной шкале, которая наиболее близко совпадает с одной из отметок на фиксированной шкале, умножьте количество делений, взятых на нониусной шкале, на 0,01 мм
Вам нужно найти отметку на нониусной шкале, которая наиболее близко совпадает с одной из отметок на фиксированной шкале, умножьте количество делений, взятых на нониусной шкале, на 0,01 мм.
Нониусное значение = количество делений × 0,01
Добавьте нониус к показаниям фиксированной шкалы, чтобы получить измеренную длину.
Измерение площади поверхности цилиндра
Предположим, что радиус основания цилиндра равен (r), а его высота (h), его площадь основания = π r², площадь боковой поверхности = окружность основания × высота = 2π rh
Определение площади основания цилиндра
Поместите основание цилиндра на лист с графиком и отметьте его основание, Снимите цилиндр и измерьте диаметр его основания (2r) линейкой, Вычислите радиус (r), а затем найдите площадь основания, которая имеет круглую форму ( π r² ).
Определение боковой площади цилиндра
Измерьте высоту цилиндра (h), вычислите длину окружности основания, которая равна = 2π r, поперечная площадь = 2π r × h
Еще один метод определения боковой поверхности цилиндра
Оберните картонный лист вокруг цилиндра ровно на один полный оборот, распрямите картонный лист, чтобы получить прямоугольник длиной, равной окружности основания, и шириной, равной высоте цилиндра, Измерьте длину этой окружности, Умножьте длину окружности на высоту, чтобы получить боковая площадь цилиндра.
См. также
| гладкий • рычажный • листовой • трубный • проволочный • призматический • канавочные • резьбомерный • зубомерный • универсальный |
| гладкий • рычажный • листовой • трубный • проволочный • призматический • канавочные • резьбомерный • зубомерный • универсальный |
| Актинометр · Анемометр · Балансомер · Барограф · Барометр · Ветроуказатель · Гелиограф · Гигрометр · Детектор испарения · Детектор молний · Дисдрометр · Облачный прожектор · Облакомер · Защитные очки · Индикатор приращения льда · Лидар · Метеозонд · Метеорологическая ракета · Нефелометр · Нефоскоп · Пиранометр · Погодный радар · Радиолокационная станция · Радиозонд · Осадкомер · Снегомер · SODAR · Соляриметр · Термограф · Термометр · Термометрическая будка · Ультразвуковой анемометр · Флюгер |
Смотреть что такое «Измерительный прибор» в других словарях:
измерительный прибор — прибор Средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне. Примечания 1. По способу индикации значений измеряемой величины измерительные приборы разделяют на показывающие и… … Справочник технического переводчика
Измерительный прибор — (датчик) – измерительный прибор (датчик) – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительный… … Энциклопедия терминов, определений и пояснений строительных материалов
ИЗМЕРИТЕЛЬНЫЙ ПРИБОР — средство измерений, дающее возможность непосредственно отсчитывать (регистрировать) значения измеряемой величины. Наиболее распространены измерительные приборы прямого действия измерительные преобразователи и измерительные приборы сравнения, в… … Большой Энциклопедический словарь
ИЗМЕРИТЕЛЬНЫЙ ПРИБОР — средство измерений, дающее возможность непосредственно отсчитывать значения измеряемой величины. В аналоговых И. п. отсчитывание производится по шкале, в цифровых по цифровому отсчётному устройству. В И. п. прямого преобразования (напр., в… … Физическая энциклопедия
измерительный прибор — средство измерений, дающее возможность непосредственно отсчитывать (регистрировать) значения измеряемой величины. Наиболее распространены измерительные приборы прямого действия измерительные преобразователи и измерительные приборы сравнения, в… … Энциклопедический словарь
измерительный прибор — matavimo priemonė statusas Aprobuotas sritis Standartizacija ir metrologija apibrėžtis Įrankis, prietaisas, sistema, skirti matuoti savarankiškai arba kartu su kitais papildomais įtaisais. atitikmenys: angl. measuring apparatus; measuring… … Lithuanian dictionary (lietuvių žodynas)
измерительный прибор — matuoklis statusas T sritis Standartizacija ir metrologija apibrėžtis Matavimo priemonė, skirta matuoti savarankiškai arba kartu su kitais papildomais įtaisais. atitikmenys: angl. measuring apparatus; measuring instrument; meter vok. Messer, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
измерительный прибор — matuoklis statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas mechaninių, elektrinių ir kitokių dydžių vertėms matuoti. atitikmenys: angl. measuring apparatus; measuring instrument; meter vok. Messer, m; Messgerät, n;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Измерить – значит, сравнить
На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.
 Из мультфильма «38 попугаев».
Из мультфильма «38 попугаев».
Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?
Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.
В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.
 (Источник)
(Источник)
Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?
Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?
Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр. На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.
Эталон длины
 (Источник)
(Источник)
Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.
Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.
 (Источник)
(Источник)
Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.
Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.

Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.
При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.
 (Источник)
(Источник)
Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.
По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:
- чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
- за основу физических величин берутся эталонные значения, то есть образец сравнения.
- для всех величин существуют свои способы, устройства и единицы измерения.
Погрешности, как проводить с учетом ошибок
Абсолютно точные измерения невозможны хотя бы потому, что измеряемые величины, да и сами эталоны единиц измерения, не имеют абсолютно точных значений. Например, масса любого тела меняется из-за испарения его собственных молекул и поглощения молекул окружающего газа. Однако в большинстве случаев точности аппаратуры не хватает, чтобы заметить эти изменения.
Для характеристики каждого конкретного измерения используют его абсолютную погрешность, т.е. модуль разности между точным значением величины и ее значением, полученным в результате измерения. Истинное значение величины узнать нельзя, но с помощью серии измерений и обработки их результатов можно найти ее приблизительное значение и оценить возможное отклонение от него измеренной величины. В этом и заключается смысл обработки результатов эксперимента.
Чтобы понимать, насколько велики ошибки по сравнению с самой измеряемой величиной, вводят относительную погрешность измерения:
Часть погрешностей связана с приборами, часть — с наблюдателем, часть — с методами обработки и расчета. Приборная погрешность проявляется из-за несовершенства измерительной аппаратуры, например, из-за большой силы трения, действующей на стрелку прибора.
Есть погрешности и у цифровых измерительных приборов, поскольку аналого-цифровые преобразователи в принципе имеют ограниченное разрешение, что приводит к нелинейности и ошибкам квантования.
В процессе измерений человек привносит субъективные погрешности. Например, точность измерения секундомером ограничена временем реакции, равным 0,1–0,2 с.
Косвенные измерения требуют расчетов, а значит, появляется погрешность вычислений, ведь при любом вычислении приходится округлять результат: даже самый точный калькулятор вместо точного значения 2/3 использует десятичную дробь конечной длины: 0,66666667. Так как расчеты ведутся по формулам, созданным на основе определенной модели явления, то может обнаружиться и погрешность метода, она же методическая погрешность. Если раз за разом измерять ускорение свободного падения, увеличивая высоту, с которой тело отправляют в полет, то рано или поздно станет заметным влияние сопротивления воздуха.
Результат измерения, как правило, число не целое, а дробное. Измеряемая величина не дискретная, а непрерывная. Повторение чисел в результатах измерений случается редко, и поэтому вероятность повтора какого-то конкретного числа крайне низка и уменьшается при росте выборки.
Формула, по которой вычисляется плотность вероятности:
Так можно вычислить истинное значение величины — ее математическое ожидание.
Ширину распределения описывают средним значением квадрата отклонения от математического ожидания. Отклонение возводят в квадрат, чтобы суммировать неотрицательные числа и не получить в сумме нуль. Эта величина называется дисперсией. В случае реальных измерений физических величин можно рассчитать только выборочное среднее и дисперсию выборки, поскольку число измерений конечно.
При записи результатов измерений соблюдаются некоторые правила. Погрешность измерения обычно округляется до одной цифры, если первая цифра, отличная от нуля, больше 2, и до двух цифр, если она меньше или равна 2. Например, если найденные в результате проведенных измерений погрешности равны ±83, ±0,0218, то их записывают так: ±80, ±0,022. В физических справочниках цифры, в которых возможна ошибка, как правило, заключены в скобки.
Физические величины и их измерение
Все физические тела обладают набором определенных свойств. Все физические явления протекают во времени. Задача физики — понять причины тех или иных физических явлений и описать их.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
Для описания какого-либо свойства физического тела и явления служит физическая величина.
Одна и та же физическая величина используется для характеристики одного и того же свойства различных физических явлений и тел.
Например, мы можем говорить о длине шага, длине стола, длине доски. При этом значения вышеперечисленных длин будут разными.
Для того чтобы количественно описать физическую величину, необходимо знать её числовое значение и единицу физической величины. Говоря о том, что урок в школе длится 45 минут, мы описываем физическую величину время. Сочетание «45 минут» — это время, показывающее длительность урока, состоящее из числового значения 45 и единиц времени минут.
ЕДИНИЦЫ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ
Говоря о значении физической величины, мы всегда должны учитывать, в каких единицах она выражена. Для каждой физической величины существуют свои единицы. Например, единицами длины могут быть сантиметр, метр, километр. Что же в этом случае означает измерить физическую величину?
Измерение физической величины – это сравнение её с эталоном. Уже более двух веков все страны мира стремятся использовать одинаковые эталоны для измерения основных физических величин. Для этот и была создана Международная система единиц СИ (система интернациональная).
| Единицы СИ | |
| Единица длины | Метр (1 м) |
| Единица времени | Секунда (1 с) |
| Единица массы | Килограмм (1 кг) |
Если сравнивать длину какого-либо тела с эталоном метра, мы получим длину, выраженную в метрах.
КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
Итак, эталоном длины служит метр. Но ведь существуют тела, обладающие совсем маленькими или очень большими размерами. Так, длина инфузории-туфельки, которая составляет примерно 0,0002 м, очень мала, а длина экватора Земли, составляющая 40 075 696 м, велика.
Эти величины часто неудобно выражать в метрах, поэтому для таких целей используют единицы, которые могут быть меньше метра в 10, 100 и т. д. раз (их называют дольными), или больше метра в 10, 100 и т. д. раз (их называют кратными).
| Название приставки | Название единицы, кратной или дольной метру | Множитель |
| милли (м) | миллиметр (мм) | 0,001 |
| санти (с) | сантиметр (см) | 0,01 |
| деци (д) | дециметр (дм) | 0,1 |
| кило (к) | километр (км) | 1000 |
Например, километр является кратной единицей для метра и равен 10(H) метрам. При этом в названии «километр» появилась приставка «кило», которая и определяет, насколько одна величина больше другой.
Для того чтобы величину, выраженную в метрах, перевести в сантиметры, необходимо её значение умножить на 100. В этом случае число 100 называют множителем.
В качестве примеров дольных единиц можно рассмотреть: единица в тысячу раз меньше метра называется миллиметр, в миллион раз меньше метра — микрометр или кратко — микрон, в миллиард раз меньше метра — нанометр.
ДЕЙСТВИЯ НАД ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ
Нельзя напрямую сравнивать две физические величины, выраженные в разных единицах.
Например, расстояние между школой и домом одного ученика равно 1 километру, а расстояние от школы до дома другого ученика — 1100 метров. Как понять, кто живёт дальше от школы?
Чтобы сравнение было правильным, нужно сначала выразить значения величин в одинаковых единицах:
1 км = 1000 м;1000 м < 1100 м.
При этом всегда надо помнить, что нельзя сравнивать неоднородные величины, например такие, как масса и расстояние, или расстояние и время. Такое сравнение не имеет никакого смысла.
Старинные меры
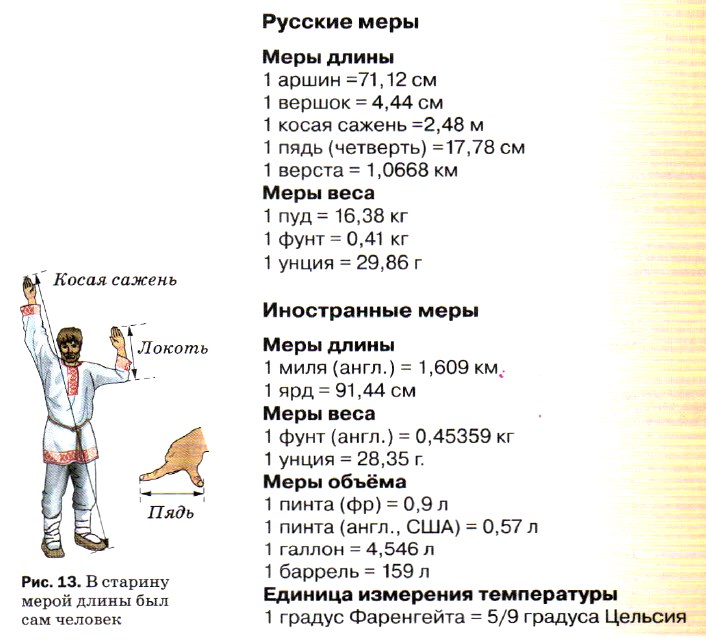
С давних времен человеку приходилось проводить измерения. В русской системе мер, которая традиционно применялась на Руси, мерой длины, например, мог быть сам человек. Так, косая сажень — это расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь или четверть — расстояние между концами расставленных большого и указательного пальцев руки.
В 1899 году наряду с русской системой мер к использованию была разрешена метрическая система.
Сегодня в России применяется Международная система единиц, а старинные меры сохранились лишь в пословицах и поговорках.
Вы смотрели конспект по физике для 7 класса «Физические величины и их измерение»: единицы физических величин, кратные и дольные физические величины, действия над физическими величинами.
Вернуться к Списку конспектов по физике (оглавление).
Пройти онлайн-тест «Наблюдения. Опыты. Физические величины»




























