Законы арифметики

Связь умножения и сложения

Ворчун любит поворчать, потому что ему не нравится, что гномов окружают одинаковые вещи.

Надо считать одинаковое количество карманов на одинаковых куртках, пальто или вычислять сложением количество деревьев в лесу. Ворчун добывает гранит. Этим камнем облицованы набережные в городах, отделаны стены домов и станций метро.

Чтобы посчитать, сколько разных цветов гранита нашел, Ворчун к трем прибавляет три четыре раза.

Получается пример:

Гном собирает коллекцию камней и минералов. В ряду четыре штуки. Посчитайте сколько ископаемых в семи рядах.

Семь раз возьмите по 4 камня. Получается длинная запись

А если рядов будет не семь, а например 60. Надо 60 раз складывать? Обязательно собьемся. В реальной жизни в магазине товар исчисляется сотнями и тысячами.

Посмотрите на розовый известняк из кладовых Земли. Из него сделали много плиток для строительства домов и дорог.

Ребята, Ворчун ворчит, а Весельчак расскажет про новое волшебное действие, которое помогает пересчитывать большие количества предметов.

Люди придумали, как сделать запись короче и вычислять быстрее. Они решили назвать это действие умножением. Получается, что операции сложения и умножения тесно связаны между собой. Умножение – особый случай сложения, когда одно число складывается много-много раз. Мы имеем дело уже не с действием сложения, а умножением.

Записывается пример так: на первое место поставьте число, которое повторяется, потом знак умножения – точку. Иногда вместо точки ставят крестик — x. На клавиатуре компьютера или смартфона знак изображают как звездочку *. На второе место запишите то число, сколько раз оно повторяется.

Давайте посмотрим, как это выглядит в жизни. Допустим, у нас есть пять книг, в каждой из них по 100 страниц.

Сколько всего страниц? Видите – здесь идет повторение одного и того же числа по 100 страниц. Поэтому надо все эти страницы сложить.

Конечно, это легче сделать умножением. Сначала напишите сто, затем точку. Посмотрите сколько раз надо взять по сто. Пять раз.

Рассмотрим другой случай. Сколько будет стоить 4 мороженых по 30 рублей за каждое?

Мы будем платить за первое мороженое 30 рублей, за второе 30, за третье 30 и за четвертое столько же.

Заменим умножение сложением: получается, что повторяется 30 рублей. Ставим на первое место 30, дальше точка и четверка.

4 раза заплатим за эти мороженые по тридцать рублей.

Решим задачу на умножение.

Бабушка сварила на зиму 6 банок варенья по 3 литра в каждой. Сколько варенья сварила бабушка?

Когда решаете задачу, всегда представляйте ее условие.

3 литра – количество варенья в банке

6 – сколько раз мы берем по шесть

3 литра ∙ 6 раз = 18 литров

Прочитайте решение: по три взять шесть раз получится восемнадцать. Или три умножить на шесть получится восемнадцать.

Таблицу умножения нужно знать наизусть. Но как быть, если еще не выучили? Вычислите умножение сложением:

Например, нужно 30 х 4. Значит надо сложить 30 четыре раза.

Фраза «умножить число пять на число три» или же «пятью три» означает «пять плюс пять, плюс пять».

Это кратчайший путь для ситуаций, когда складывается много раз одно и то же число.

В записи операции умножения первое число называется первый множитель, второе число — второй множитель, а результат умножения называется произведением.

Запомните друзья, умножение – это действие, которое увеличивает число. Берем маленькое число несколько раз, получается большое число

Это важно помнить

Когда появилась таблица умножения?

Прежде чем говорить о том, когда появилась таблица умножения, давайте вспомним, что это вообще такое. Таблица умножения – это математическая таблица, которую мы используем, чтобы получить произведение от умножения чисел от 1 до 9 друг на друга. Сегодня она не вызывает у нас никакого удивления и мы воспринимаем ее, как нечто само собой разумеющееся. Но так было далеко не всегда, и история таблицы умножения тому подтверждение.

Научные данные вряд ли ответят нам на вопрос, в каком году появилась таблица умножения. Точности здесь нет. Старейшие из известных человечеству таблиц умножения ученые относят еще к временам Месопотамии, а точнее, Вавилона. Однако тогда, около 4 тыс. лет назад, люди пользовались шестидесятеричной системой исчисления, изобретенной древними шумерами.

Найденный археологами, вероятнее всего, самый старый из всех известных математических текстов наглядно показывает соотношение сторон шести прямоугольников 1:60 и говорит о том, что математика, которую преподавали в школах писцов в Шумере вплоть до середины третьего тысячелетия до н.э., была крайне сложной. По мнению специалистов, практической пользы от такой математики был минимум. По сути, это была математика ради математики.

Мы же с вами пользуемся десятичной системой. Десятичная таблица умножения признана неотъемлемой частью элементарной арифметики по всему миру, т.к. является основой для арифметических операций с десятичными числами, а большинство педагогов рекомендуют заучивать таблицу до 9*9.

Наиболее известной таблицей, основу которой составляет десятичная система, считается китайская таблица умножения на бамбуковых полосках. Еще недавно самыми старыми китайскими таблицами умножения были экземпляры, относящиеся к периоду династии Цинь между 221 и 206 годами до н.э. Это серии коротких предложений (например, «шесть восьмерок порождают сорок восемь»), допускающие лишь самые простые умножения.

Но несколько лет назад Университету Цинхуа в Пекине передали в дар 2500 бамбуковых полосок. Их, покрытые грязью и плесенью обнаружили, скорее всего, при незаконных археологических раскопках, а сам даритель приобрел их на рынке в Гонконге.

По мере изучения китайские специалисты не только смогли датировать их 305 годом до н.э., что относится к периоду Сражающихся царств Китая, но и собрали из отдельных фрагментов (бамбуковых полосок) в одно целое то, что потом назвали старейшим образцом таблицы умножения с основанием 10.

Записи на пересечениях строк и столбцов, как и в современной таблице умножения, на древнекитайском образце – это результаты умножения чисел. При этом с помощью таблицы можно умножать как целые числа, так и числа от 0,5 до 99,5. А числа, не представленные напрямую, сначала нужно преобразовать в серию сложений. Они, в свою очередь, приводят к серии отдельных умножений, которые считаются по таблице. И уже после сложения всех ответов получается окончательный результат.

Ученые считают, что эта таблица широко применялась чиновниками с целью рассчитать суммы налогов, урожайность сельхоз культур или площадь земли. Но все же уверенности в том, что в те времена производились такие сложные вычисления, нет. Однако найденный образец сегодня по факту является примером самой первой десятичной таблицы умножения.

Кто придумал таблицу умножения?

Бытует мнение, что Пифагор, но это нет так. Таблица умножения существовала еще 4000 лет назад в самых разных вариантах. Точный ее создатель не известен, но она имеет свои корни из древнего мира и относится к самым ранним цивилизациям.

Существует версия, что таблицу умножения придумали параллельно в разных концах планеты, поскольку с необходимостью производить подсчеты больших чисел люди в те времена сталкивались повсеместно.

Таблица умножения в Новое время

В периоды Средневековья, Возрождения и Нового времени, вплоть до Новейшего времени, существенных изменений в таблице не происходило, но история таблицы умножения продолжалась. В источниках можно найти информацию о том, что в Европе первая таблица умножения впервые появилась в средневековой Англии, и, как и сейчас, представляла собой систему перемножения чисел на 12. Вопрос же о том, какова история возникновения таблицы умножения, был не так популярен.

В разные периоды (1168 год, 1484 год, 1489 год) в работах некоторых специалистов, таких как Никола Шюке, Иоганн Видман и другие, периодически появлялись треугольные и пирамидальные таблицы умножения.

В 16 веке энциклопедист Джон Непер создал свой способ умножения и деления с помощью специальных палочек с обозначенными на них цифрами. Позже их стали называть неперовыми палочками. Они существенно упростили работу людей с цифрами и пользовались популярностью вплоть до 19 века, позже став прообразом современной счетной линейки.

Не менее известен и метод решетчатого умножения (иногда его называют «китайской решеткой» или сеточным умножением). Он был распространен во многих культурах (к примеру, в Древней Греции и Индии), а смысл был в том, что для умножения двух многозначных чисел использовалась специальная секта, в которой все ячейки разбиты по диагонали. Сетка позволяла умножать большое количество цифр.

Крометого, в 1820 году был опубликован труд «Философия арифметики» шотландского математика и физика Джона Лесли. В нем автор представил таблицу умножения до 99, которая позволяла умножить числа на пары цифр всего за один раз. Позже Лесли стал преподавать эту таблицу ученикам, и при этом рекомендовал заучивать ее до 50*50 (по другим данным, до 25*25).

Сегодня же практически везде используется уже ставшая обычной таблица умножения, заканчивающаяся на 9*9. Несколько непривычный для нас вариант существует в Англии, где до сих пор считают точно так же, как в Средневековье, т.е. таблица там заканчивается на 12*12. Это связано с английской измерительной системой, где есть футы и дюймы (1 фут = 12 дюймов); к тому же раньше в денежном обращении был шиллинг, равный 12 пенсам.

И еще одна несколько необычная таблица умножения распространена в Индии – там она заканчивается на 20*20. А в Китае применяется таблица меньшего размера, где нет первого столбца, поскольку единица считается мультипликативным тождеством.

Как быстро и легко выучить таблицу умножения: лучшие способы

Вот несколько простых для понимания и отлично работающих способов для изучения таблицы умножения вместе с ребёнком:

Таблица Пифагора

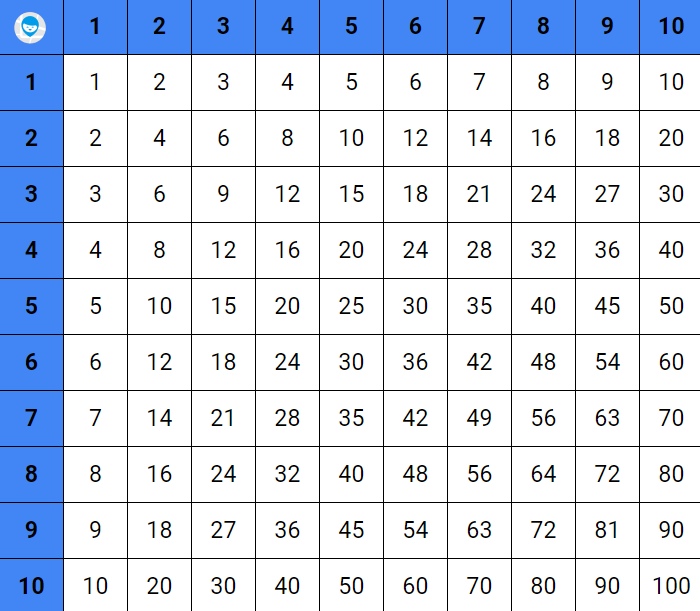
Prostock-studio/Shutterstock.com

Классическая для российского образования схема таблицы умножения может испугать объёмом — выходит, что школьнику придётся учить целых сто примеров.

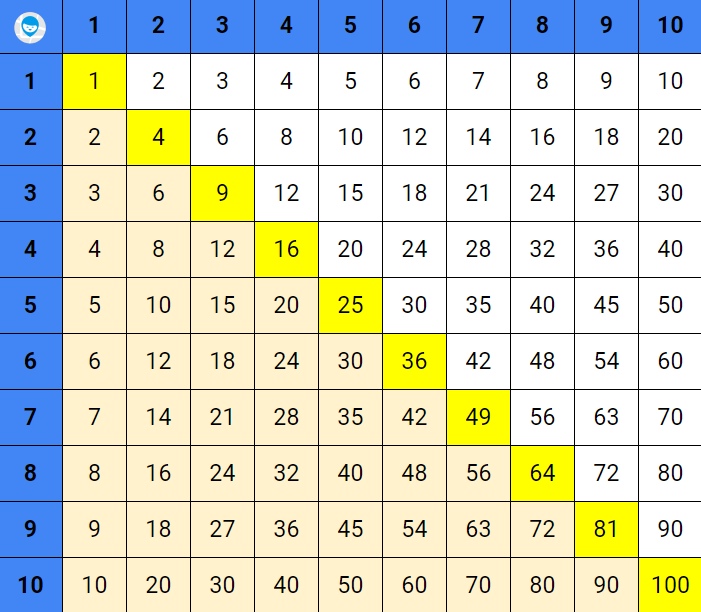
Замените привычную таблицу таблицей Пифагора, и вместо 100 арифметических действий останется запомнить всего 36.

Как освоить умножение с помощью таблицы Пифагора:

1. Сделайте таблицу Пифагора, в которой будут указаны только множители.

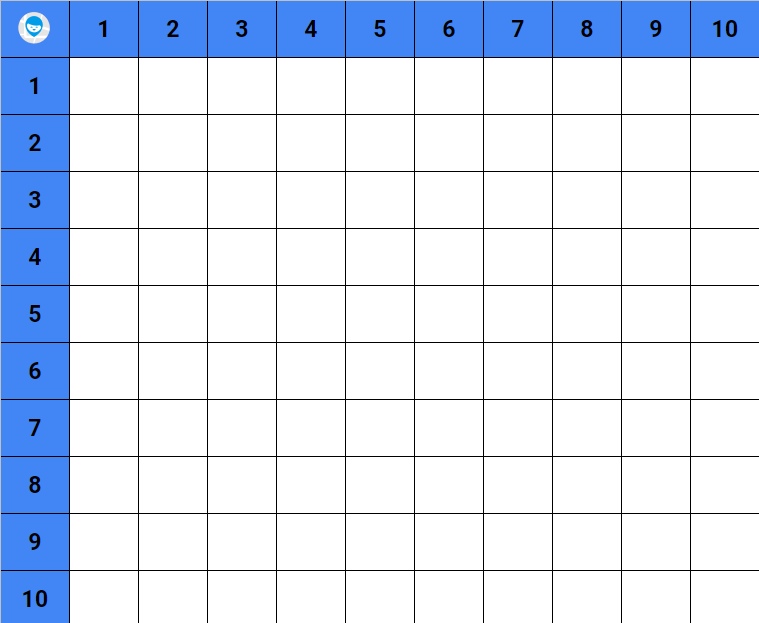
Prostock-studio/Shutterstock.com

2. Вместе с ребёнком заполните пустые клетки. Со многими примерами младший школьник справится самостоятельно. Расскажите, что достаточно сложить 2 и 2, и дальше к каждой полученной сумме прибавлять 2: 2 + 2 = 4, 4 + 2 = 6, 6 + 2 = 8 и т.д.

Таким же способом заполните клетки с остальными множителями: 3 + 3 = 6, 6 + 3 = 9; 4 + 4 = 8, 8 + 4 = 12, и т.д.

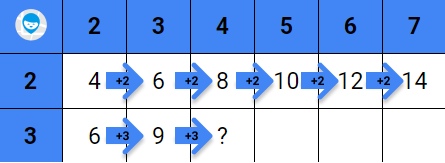
Prostock-studio/Shutterstock.com

3

Обратите внимание ребёнка на то, что, аналогично принципу сложения, в умножении от перемены множителей результат не меняется: например, если умножать числа 4 на 6 или 6 на 4 — получается 24 в обоих случаях

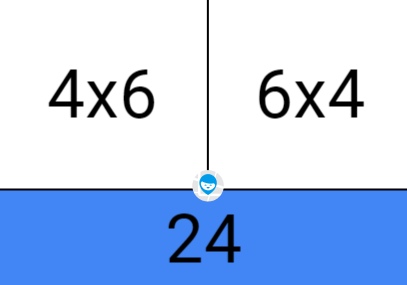
Prostock-studio/Shutterstock.com

4. Помогите сыну или дочери прийти к выводу, что почти половина примеров повторяется, только множители меняются местами – остаётся запомнить 55 примеров вместо 100.

Prostock-studio/Shutterstock.com

5. Подскажите другие закономерности, которые не нужно заучивать:

• число, умноженное на единицу, остаётся равным самому себе;
• при умножении на 10 достаточно дописать к числу 0, чтобы получить правильный ответ (2 х 10 = 20, 3 х 10 = 30 и т.д.).

Благодаря изучению таблицы умножения с помощью таблицы Пифагора ребёнку останется выучить всего 36 примеров вместо ста.

Карточки умножения

Prostock-studio/Shutterstock.com

Можно использовать готовые карточки или сделать их самостоятельно — так ребёнок начнёт запоминать таблицу сразу в процессе подготовки карточек.

Как выучить таблицу с помощью карточек:

• на небольшом листе бумаги ребёнок пишет действие, на обратной стороне этого же листа — правильный ответ (например, на лицевой стороне — 6 х 7, на обратной — 42);
• можно прописать на карточках все примеры из таблицы, позже оставить только те, которые вызывают у ребёнка затруднения;
• добавьте в обучение элементы игры: можно поставить цель дать сто верных ответов из ста или называть результаты умножения на скорость.

Настольные игры

Особенно хорошо способ подходит для неусидчивых детей: достаточно сложная информация постепенно запоминается в форме занимательной игры. Можно использовать уже готовые игры, которые построены на принципах умножения или умножения и деления (деление также предстоит изучить во втором классе). Например, настольная игра «Много-Много» или «Цветариум».

Ещё один вариант — играть в обычные «ходилки» с изменёнными правилами: договориться, что выпавшее количество ходов будет умножаться на 2, 3 или на любую другую цифру меньше или равную 10.

От простого к сложному

Prostock-studio/Shutterstock.com

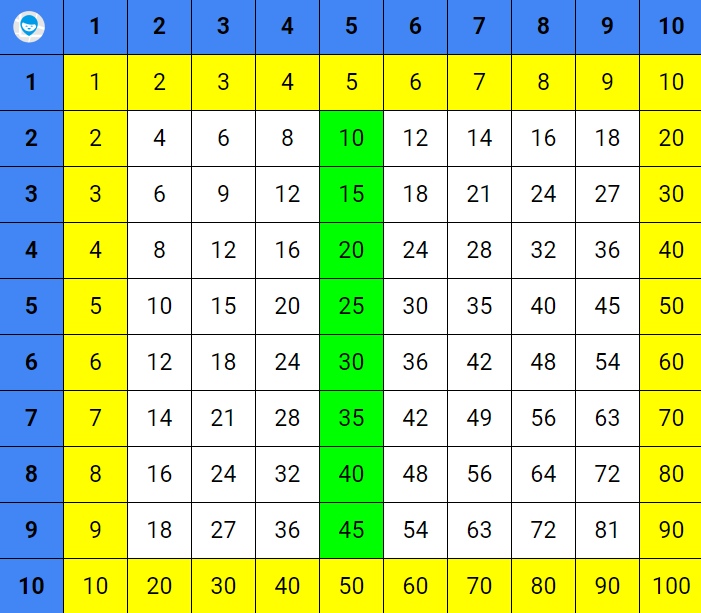
Дети легче запоминают таблицу, когда учат примеры не подряд, а переходят от простых к более трудным. Попробуйте выучить умножение в таком порядке:

• единицы и десятки: самые простые примеры, с которыми обычно проблем не возникает (число, помноженное на 1, остаётся прежним; к умноженному на 10 добавляется 0);
• на 5: при умножении чётного числа на 5 обязательно получится чётное число, оканчивающееся на ноль (2 х 5 = 10, 4 х 5 = 20), при умножении нечётного числа на 5 получится нечётное число, оканчивающееся на 5 (7 х 5 = 35, 9 х 5 = 45);
• на 2 и на 4: умножение на 2 — это всегда одно и то же число, сложенное с собой (2 х 2 = 4, 3 х 2 = 6); на 4 — то же, что и умножение на 2, но увеличенное в два раза, то есть можно умножить число на 2 и прибавить к нему то же самое число (2 х 4 = 2 х 2 + 4 = 8);
• на 9. Проще всего запомнить с помощью пальцев:
  1. пусть ребёнок повернёт ладони вверх и мысленно даст пальцам номера от 1 до 10, считая слева направо (начиная с большого пальца левой руки),
  2. попросите ребёнка загнуть тот палец по счёту, который соответствует цифре, умножаемой на 9,
  3. например, при умножении 3 на 9 нужно загнуть третий слева палец, оставшиеся разогнутыми два пальца слева — это десятки, семь пальцев справа — единицы, в итоге получается 3 х 9 = 27;
• на 3, 6, 7, 8: можно выучить наизусть или подключить другие способы – карточки, плакаты, рифмы, настольные игры, попробовать учить на пальцах.

Таблица умножения в России и СССР

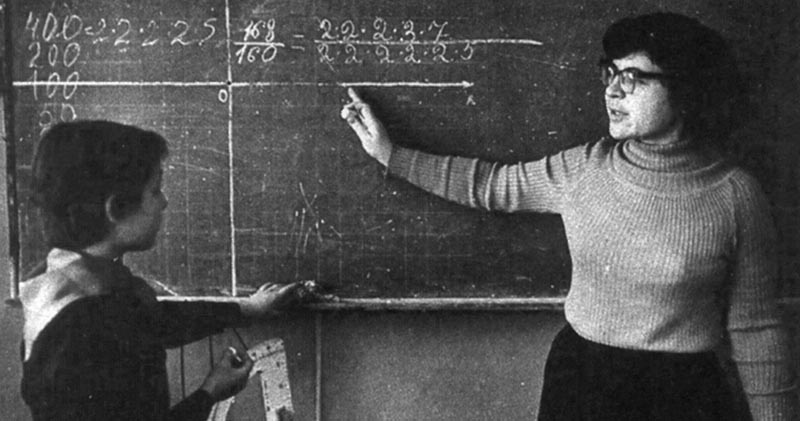
Какова же история таблицы умножения в России? В каком году появилась? Кто положил начало ее использованию русскими людьми?

На Руси использовали крестьянский способ умножения, смысл которого сводился к тому, что первый множитель увеличивали в два раза, а второй в два раза уменьшали. И таким образом поступали до момента, пока второй множитель не становился равен одному. Строки, где правое число было четным, просто удалялись, а сумма левых чисел и оставшихся строк показывала искомый результат. При таком способе счета таблица умножения попросту не требовалась, а работать так можно было с любыми многозначными числами.

В России таблица умножения впервые появилась в 1682 году. Ее напечатали в первой русской книге по математике, которая называлась «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи…». Это был своеобразный сборник таблиц с цифрами, и любой, кто занимался куплей или продажей, мог получить в руки инструмент для быстрого счета.

В этой книге можно было увидеть пары чисел от 1*1 до 100*100, а все записи велись славянскими цифрами. Примечательно, что это первое издание почти не пользовалось спросом, а вот второе, напечатанное в 1714 году уже гражданским шрифтом и индийскими цифрами, разошлось тиражом более 700 экземпляров, что было очень неплохо для того времени. Кстати, сегодня по одному образцу данной книги можно найти в Научной библиотеке МГУ и Российской государственной библиотеке.

В 1703 году свет увидел первый учебник по математике «Арифметика», автором которого был математик Леонтий Филиппович Магницкий. И в этом учебнике уже можно было найти более понятные обывателю таблицы умножения и сложения. Представлены он были, конечно, не совсем в привычном для нас виде, но понять, что к чему, не составляло никакого труда.

Со временем по этой книге стали обучаться абсолютно все, а выдающийся русский ученый Михаил Васильевич Ломоносов назвал ее «вратами учености». Несколько экземпляров труда Магницкого хранятся в Отделе редких книг и рукописей библиотеки Московского университета.

Когда же заучивание таблицы умножения стало в России обязательным, это оказалось революционным событием, впоследствии облегчившим как повседневные расчеты и вычисления, так и быт и работу людей в целом. Сегодня же без знания таблицы умножения представить свою жизнь попросту невозможно, а встретить ее можно на любой школьной тетрадке в клеточку.

Свойства группы для вычислений

Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.

Алгоритм оптимизированного решения:

1. к последнему элементу ряда добавляют 1;
2. результат делят на два;
3. полученное значение возводят в квадрат, т. е. определяют произведение умножения его на самое себя.

Примеры логических задач для решения через характеристику парности:

1. Можно ли доску, разбитую на определенное количество клеток, заполнить костями домино, чтобы каждое значение располагалось в отдельной ячейке?
2. Группа детей, среди которых пять мальчиков, встали в круг, взявшись за руки. Сколько всего малышей, если известно, что соблюдено чередование девочек и ребят?
3. Могут ли 11 шестеренок, расположенных на плоскости, вращаться одновременно?
4. Получится ли разменять купюру в 25 единиц с помощью банкнот значением 1, 3 и 5?

Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.

Техники, упрощающие процесс изучения

Существует несколько способов облегчить процесс обучения.

Учеба при помощи карт

Предлагается следующая детская игра: положить на стол рубашкой вверх по 10 карт из колоды на игрока. Дети должны одновременно выбрать любую карту и перевернуть ее. Тот, кто первый правильно умножит два числа на картах, получает один балл. Играть можно до любого предела.

Еще один вариант игры — записать на небольших карточках значения произведений любых чисел, встречающихся в таблице. Задача участников — сказать, какие числа, умноженные друг на друга, дадут такое значение.

Можно также записать на одной стороне листочка перемножаемые числа, а на другой — правильный ответ. Если ребенок отвечает верно, карточка откладывается на дальнейшее повторение, если нет — складывается в колоду для учебы. Данный вариант применяется для закрепления выученного.

Преимущества карточек состоят в том, что у детей, играющих в них, тренируется зрительная и слуховая память, когда происходит озвучивание ответа.

Практические задачки

Они особенно актуальны, когда речь идет о запоминании наиболее трудных комбинаций (произведение на 6, 7, 8). Примеры следует приводить из ежедневной деятельности для упрощения восприятия и запуска работы ассоциаций.

Обучающие стихи

Можно использовать имеющиеся в интернете стихотворения, либо придумывать легкие двустишия, возможно, даже не имеющие смысла.

Фрагменты стихотворений А. Усачева и М. Казариной

Использование карандашей

Часто примеры умножения показывают при помощи карандашей, ручек и т. п. Одинаковое количество того или иного вида канцелярских принадлежностей раздают каждому члену семьи и просят посчитать, сколько всего штук есть у всех. В итоге делается вывод, что это и есть число карандашей, умноженное на количество членов семьи.

Визуализация

Если малыш, которому предстоит изучить таблицу, обладает развитым образным мышлением и воображением, можно предложить ему нарисовать для каждой цифры собственную историю, использовав яркие фигуры, разные цвета для каждого числа.

Работает также следующая методика — необходимо разделить по стаканам одинаковое количество карандашей так, чтобы в каждой емкости находились предметы одного цвета. После подсчета объясняется, что общее количество карандашей — это результат их умножения в одном стакане на количество стаканов.

Смена обстановки

Рекомендуется также применять подсчеты вне домашней обстановки, например, на улице или в магазине. Можно попросить ребенка с помощью умножения определить количество колес у четырех автомобилей, у трех велосипедов, количество лап у двух играющих рядом собак и т. д.

Практическое применение

Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.

В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.

Таблица умножения

1 × 1 = 1	2 × 1 = 2	3 × 1 = 3	4 × 1 = 4	5 × 1 = 5
1 × 2 = 2	2 × 2 = 4	3 × 2 = 6	4 × 2 = 8	5 × 2 = 10
1 × 3 = 3	2 × 3 = 6	3 × 3 = 9	4 × 3 = 12	5 × 3 = 15
1 × 4 = 4	2 × 4 = 8	3 × 4 = 12	4 × 4 = 16	5 × 4 = 20
1 × 5 = 5	2 × 5 = 10	3 × 5 = 15	4 × 5 = 20	5 × 5 = 25
1 × 6 = 6	2 × 6 = 12	3 × 6 = 18	4 × 6 = 24	5 × 6 = 30
1 × 7 = 7	2 × 7 = 14	3 × 7 = 21	4 × 7 = 28	5 × 7 = 35
1 × 8 = 8	2 × 8 = 16	3 × 8 = 24	4 × 8 = 32	5 × 8 = 40
1 × 9 = 9	2 × 9 = 18	3 × 9 = 27	4 × 9 = 36	5 × 9 = 45
1 × 10 = 10	2 × 10 = 20	3 × 10 = 30	4 × 10 = 40	5 × 10 = 50
6 × 1 = 6	7 × 1 = 7	8 × 1 = 8	9 × 1 = 9	10 × 1 = 10
6 × 2 = 12	7 × 2 = 14	8 × 2 = 16	9 × 2 = 18	10 × 2 = 20
6 × 3 = 18	7 × 3 = 21	8 × 3 = 24	9 × 3 = 27	10 × 3 = 30
6 × 4 = 24	7 × 4 = 28	8 × 4 = 32	9 × 4 = 36	10 × 4 = 40
6 × 5 = 30	7 × 5 = 35	8 × 5 = 40	9 × 5 = 45	10 × 5 = 50
6 × 6 = 36	7 × 6 = 42	8 × 6 = 48	9 × 6 = 54	10 × 6 = 60
6 × 7 = 42	7 × 7 = 49	8 × 7 = 56	9 × 7 = 63	10 × 7 = 70
6 × 8 = 48	7 × 8 = 56	8 × 8 = 64	9 × 8 = 72	10 × 8 = 80
6 × 9 = 54	7 × 9 = 63	8 × 9 = 72	9 × 9 = 81	10 × 9 = 90
6 × 10 = 60	7 × 10 = 70	8 × 10 = 80	9 × 10 = 90	10 × 10 = 100

Скачать

Таблица Пифагора от 1 до 10

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Скачать

Таблица Пифагора от 1 до 20

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Скачать

Сумма, произведение, частное четных (нечетных) чисел

Утверждение 1. Сумма двух четных чисел — четное число.

Доказательство. Пусть числа m и n являются четными. Докажем, что число r = m + n также четно. m=2k, n=2p, где k и p — целые числа. Тогда r = m + n = 2k + 2p = 2(k + p) = 2s. Если числа k и p являются целыми, то их сумма s — тоже целое число. Мы доказали, что число r может быть представлено в виде произведения двойки и целого числа. Доказательство завершено.

Утверждение 2. Сумма двух нечетных чисел — четное число. Докажите самостоятельно.

Утверждение 3. Сумма четного и нечетного чисел — нечетное число. Докажите самостоятельно.

Утверждение 4. Произведение двух нечетных чисел — нечетное число.

Доказательство. Пусть числа m и n являются нечетными. Докажем, что число r = m • n также нечетно.
m = 2k + 1, n = 2p + 1, где k и p — целые числа.
Тогда r = m • n = (2k+1) • (2p+1) = 4kp + 2k + 2p + 1 = 2(2kp + k + p) + 1 = 2s + 1.
Если числа k и p являются целыми, то число s = 2kp + k + p — тоже целое число.
Мы доказали, что число r может быть представлено в виде r = 2s + 1, следовательно, является нечетным. Ч. т. д.

Утверждение 5. Произведение двух четных чисел — четное число. Докажите самостоятельно.

Утверждение 6. Произведение четного и нечетного чисел — четное число. Докажите самостоятельно.

А если мы поделим четное число на четное (не равное нулю)? Что получим: чет или нечет? Естественно, однозначного ответа дать нельзя. Например, при делении 12 на 4 мы получаем нечетный результат, а при делении 32 на 4 — четный.

Если вы уже заскучали, переходите ко 2-й части статьи. Потом всегда сможете вернуться. Если же все эти теоретические построения вас не слишком утомили, давайте продолжим.

А почему, собственно, мы рассматриваем только два числа. Давайте мыслить шире!

Утверждение 7. Сумма любого количества четных чисел четна.

Доказательство. Пусть числа M₁, M₂, …, M_N являются четными, тогда их можно представить в виде 2K₁, 2K₂, … , 2K_N, где K₁, K₂, …, K_N — целые числа.
Тогда: M₁ + M₂ + … + M_N = 2K₁ + 2K₂ + … + 2K_N = 2( K₁ + K₂ + … + K_N) = 2S, где S-целое число. Четность доказана.

Утверждение 8. Сумма четного количества нечетных чисел четна. Сумма нечетного количества нечетных чисел нечетна. Докажите самостоятельно.

Утверждение 9. Произведение может быть нечетным только в том случае, если все сомножители нечетны. Докажите самостоятельно.

Так, сумма 2+4+6+…+1022+1024 четна, поскольку все слагаемые четны. Сумма 1+3+5+7+9 нечетна, т. к. содержит 5 нечетных слагаемых. Произведение 2*3*4*…*1001*1002 четно уже хотя бы по той причине, что первый сомножитель является четным.

Задание 4. Четными или нечетными будут следующие выражения: а) 2+12+22+…+1002+1012+1022, б) 1+11+111+…+111111+1111111, в) 3*13*23*…*10003*10013*10023, г) 2*3*4*…*12357891 ?

Задание 5. Докажите, что произведение всех простых чисел, не превосходящих 1000000, четно. Докажите, что произведение любого количества простых чисел, каждое из которых больше 100, нечетно. Напомню, что натуральное число называется простым, если делится только на себя и на 1.