Свойство сложения с нулем.
При сложении числа с нулем, в результате сумма будет тем же самым числом.
3+0=3
0+3=3
3+0=0+3
В буквенном выражение сложение с нулем будет выглядеть так:
a+0=a 0+a=a
Вопросы по теме сложение натуральных чисел:Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:
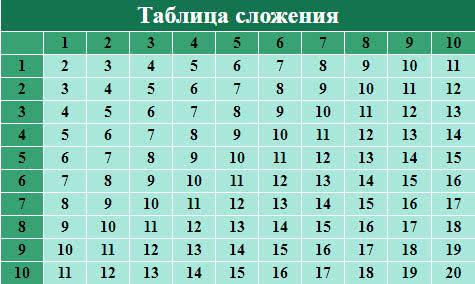 Второй вариант таблицы сложения.
Второй вариант таблицы сложения.
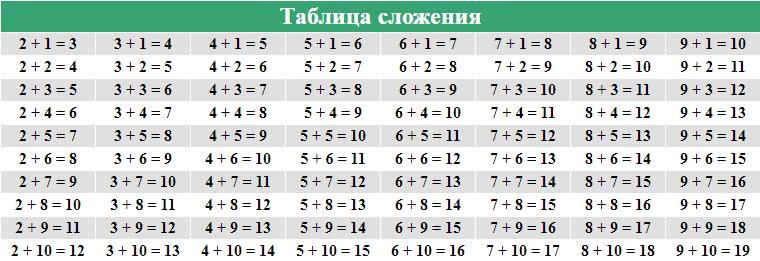 Если посмотрим на таблицы сложения, видно как работает переместительный закон.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.
В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.
В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.
Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.
Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a
Примеры на задачи.Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22
Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.
Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921
Использование свойства сложения в финансовых расчетах
В финансовой сфере свойство сложения часто используется для вычисления общей суммы денежных средств или активов. Например, при подсчете общего объема продаж за определенный период, необходимо сложить суммы каждой отдельной продажи. Также свойство сложения можно применять для расчета общей стоимости инвестиций или для определения общего размера задолженности.
| Период | Продажи |
|---|---|
| Январь | 5000 |
| Февраль | 7000 |
| Март | 6000 |
| Итого | 18000 |
Приведенная выше таблица демонстрирует использование свойства сложения для вычисления общего объема продаж за первый квартал года. Путем сложения отдельных сумм продаж можно определить, что общая сумма продаж в данном периоде составляет 18000 рублей.
Таким образом, использование свойства сложения в финансовых расчетах позволяет легко и удобно вычислять сумму различных финансовых величин и делать выводы о их общем значении.
Упражнения на свойствах сложения
Упражнение № 1
Примените коммутативные и ассоциативные свойства для подробного примера:

разрешение
У нас есть числа 2, 1 и 3 в обоих членах равенства, представленные в прямоугольниках желтого, зеленого и синего соответственно. На рисунке представлено применение коммутативного свойства, порядок добавления не меняет результат суммирования:
- 1 + 2 + 3 = 2 + 3 + 1
- 6 = 6
Взяв номера 2, 1 и 3 иллюстрации, вы можете применить ассоциативность к обоим членам равенства, получив одинаковый результат:
- (3 + 1) + 2 = 1 + (3 + 2)
- 6 = 6
Упражнение № 2
Укажите число и свойство, которые применяются в следующих утверждениях:
- 32 + _____ = 32 __________________
- 45 + 28 = 28 + _____ __________________
- (15 + _____) + 24 = 39 + (24 + 15) _________________
- (_____ + 49) — 50 = 49 + (35 — 50) __________________
ответы
- Соответствующее число равно 0, а свойство является аддитивным тождеством..
- Число 45, и свойство является коммутативным.
- Число 39, и свойство является ассоциативным.
- Число 35, и свойство является ассоциативным.
Упражнение № 3
Заполните соответствующий ответ в следующих утверждениях.
- Свойство, в которое производится добавление независимо от порядка добавления, называется _____________.
- _______________ является свойством дополнения, в котором сгруппированы два или более добавлений, в обоих членах равенства.
- ________________ — это свойство сложения, в котором нулевой элемент добавляется к числу в обоих членах равенства.
Упражнение № 4
У них есть 39 человек для работы в 3 рабочих командах. Применяя ассоциативное свойство, объясните, как будет 2 варианта.
В первом равноправном члене вы можете разместить 3 рабочих команды по 13, 12 и 14 человек соответственно. Дополнения 12 и 14 связаны.
Во втором члене равноправия 3 рабочие команды могут быть размещены в 15, 13 и 11 человек соответственно. Дополнения 15 и 13 связаны.
Применяется ассоциативное свойство, получая одинаковый результат у обоих членов равенства:
- 13 + (12 + 14) = (15 + 13) + 14
- 39 = 39
Упражнение № 5
В банке есть 3 билетные кассы, которые обслуживают 165 клиентов в группах по 65, 48 и 52 человека, соответственно, для внесения вкладов и снятия денег. Применить коммутативное свойство.
В первом члене равенства добавляются 65, 48 и 52 для касс 1, 2 и 3.
Во втором члене равенства добавляются 48, 52 и 65 для билетных касс 1, 2 и 3..
Коммутативное свойство применяется, поскольку порядок добавления в обоих членах равенства не влияет на результат суммы:
- 65 + 48 + 52 = 48 + 52 + 65
- 166 = 166
Дополнение является фундаментальной операцией, которую можно объяснить множеством примеров повседневной жизни через ее свойства..
В области образования рекомендуется использовать повседневные примеры, чтобы учащиеся могли лучше понять концепции фундаментальных базовых операций..
ссылки
- Уивер, А. (2012). Арифметика: Учебник по математике 01. Нью-Йорк, Колледж Бронкса.
- Практические подходы к разработке умственных математических стратегий для сложения и вычитания, Услуги профессионального развития для учителей. Получено из: pdst.ie.
- Свойства сложения и умножения. Получено с: gocruisers.org.
- Свойства сложения и вычитания. Получено с: eduplace.com.
- Математические свойства. Получено с: walnuthillseagles.com.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + ![]()
Решение:
3 × (7 + ![]() = 3 × 7 + 3 × 8 = 21 + 24 = 45
= 3 × 7 + 3 × 8 = 21 + 24 = 45
Задание 2. Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + ![]()
Решение:
5 × (6 + ![]() = 5 × 6 + 5 × 8 = 30 + 40 = 70
= 5 × 6 + 5 × 8 = 30 + 40 = 70
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Сложение в 5 классе: базовые понятия и операции
Сложение – одна из основных операций арифметики, которую изучают в начальной школе. В пятом классе ученики уже знакомятся с основными правилами и приемами для выполнения сложения.
Сложение выполняется с помощью знака «+». Производится сложение двух или более чисел, которые называются слагаемыми. Результат сложения называется суммой.
Основные правила сложения в 5 классе:
- При сложении чисел с одинаковым знаком, складываем их абсолютные значения и сохраняем знак;
- При сложении чисел с разными знаками, вычитаем из большего по абсолютной величине числа меньшее и сохраняем знак большего числа;
- При сложении чисел с нулем, получаем в результате другое число;
- При сложении десятков, сотен и тысяч необходимо складывать разряды по порядку, начиная с младшего;
- При сложении чисел с остатком, можно использовать перенос единицы из предыдущего разряда;
При выполнении сложения ученикам помогает использование приемов и таблиц сложения, которые тренируются на уроках математики. Также, для ускорения и упрощения подсчета, можно использовать приемы распределительного закона.
Знание и понимание основных правил сложения в 5 классе является основой для дальнейшего изучения сложения с многозначными числами и основных операций арифметики.
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Задачи на нахождение неизвестного слагаемого
Ребята, помогите Пятачку и Винни – Пуху найти вторую половинку правила:

Это правило пригодится нам, чтобы верно решить задачу.
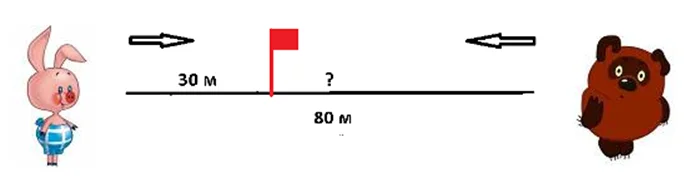
Посмотрите, Пятачок и Винни – Пух идут друг к другу в гости. Дорожка длиной 80 м. Пятачок прошел до встречи 30 м. Сколько метров прошел до встречи Винни – Пух?
Схема нам поможет понять задачу.
Сколько прошел Пятачок? 30 м.
А сколько прошел Винни – Пух? Не знаем.
Из чего состоит длина дорожки? Из расстояния, которое прошли Пятачок и Винни – Пух вместе.
Это можно записать так: 30 + ? = 80 (м)
С1 + С2 = С
Что неизвестно? Второе слагаемое.
Как его найти? С2 = С – С1
Решение: 80 – 30 = 50 (м) – прошел до встречи Винни – Пух.
Ответ: 50 метров.
Сложение с помощью координатного луча
А сейчас давайте познакомимся с другим способом счета — c помощью координатного луча.
Решим пример: $3+4$.
Нарисуем луч, на котором отметим числа по порядку: $0, 1, 2, 3…$
Рисунок $2$ Координатный луч
Нам нужно к $3$ прибавить $4$. Отметим тройку на координатном луче (рисунок $3$):
Рисунок $3$
Чтобы прибавить $4$, нам нужно «прошагать» по лучу вправо четыре шага. И посмотреть, к какому числу мы придем.
Рисунок $4$ Вычисление с помощью координатного луча
Мы пришли к семерке. Это и будет наш ответ. Вот так просто.
$3 + 4 = 7$
Для того, чтобы сложить числа от $0$ до $25$, в качестве координатного луча можно использовать школьную линейку:
Со временем вы будете совершать эти операции в уме не задумываясь. Потренируйтесь на нашем тренажёре сложения в пределах 10.
{"questions":[{"content":"Сложите с помощью координатного луча числа $3$ и $5$:`image-8`<br />`choice-1`","widgets":{"choice-1":{"type":"choice","options":,"answer":},"image-8":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/positive-coord-3.svg"}},"step":1,"hints":}]}
Задачи повышенной сложности
Ребята, поможем нашим героям справиться с задачами повышенной сложности. Научим их и научимся сами рассуждать, логически мыслить.
В лесной школе прошла математическая олимпиада. В финал олимпиады вышли две белки и два зайца. Все вместе они решили 11 задач: каждый – разное количество. Кто решил больше задач: зайцы или белки, если один заяц решил задач больше всех, а другой заяц – меньше всех.
Для решения этой задачи надо подбирать разные числа и проверять, подходят ли они.
Для удобства начертим таблицу.
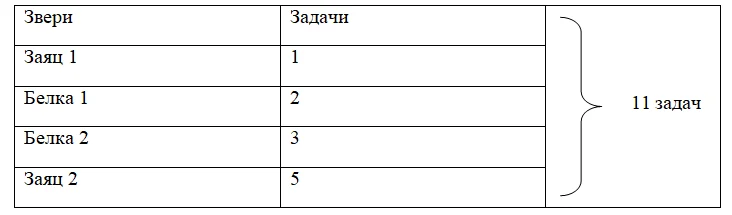
Нужно в сумме набрать 11 так, чтобы все слагаемые были разные. Пусть первый заяц решит всего 1 задачу (меньше всех). Белки решат разное количество, например, 2 и 3. Ну а второй заяц решит больше всех – это 5.
1 + 2 + 3 + 5 = 11. В сумме получилось 11 задач.
Значит, зайцы решили: 1 + 5 = 6, белки решили: 2 + 3 = 5.
6 > 5
Ответ: зайцы решили задач больше, чем белки.
Сегодня в лесной школе все с увлечением мастерили фигурки в технике оригами.
У Пятачка, Винни – Пуха и Кролика есть 3 бумажные фигурки — оригами: лиса, птичка и кораблик. По одной – у каждого. Известно, что у Пятачка – не кораблик, у Кролика и Пятачка – не лиса. У кого какая фигурка?
Давайте рассуждать вместе! Чертим таблицу.
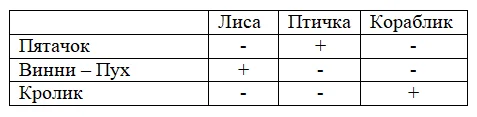
Поставим знак « – »в ячейке напротив героев сказки. Мы знаем, что у Пятачка – не кораблик и не лиса. У него – птичка, значит, у Кролика птички нет, и ему остается кораблик. А у Винни – Пуха – фигурка лисы.

Молодцы, ребята! Приходите еще, порешаем вместе! А теперь проверьте свои знания. Всем пока!
Значение свойства сложения в математике
Свойство сложения позволяет комбинировать числа и получать сумму, которая является результатом операции сложения. При сложении двух чисел, их сумма равна сумме отдельных значений каждого числа. Например, сумма 3 и 5 будет равна 8.
Свойство сложения также является коммутативным, что означает, что порядок слагаемых не влияет на результат. То есть, при сложении двух чисел, результат будет одинаковым независимо от того, какое число будет первым и какое — вторым. Например, сумма 3 и 5 будет равна сумме 5 и 3, то есть 8.
Следующая таблица иллюстрирует свойства сложения:
| Свойство | Пример |
|---|---|
| Коммутативность | 3 + 5 = 5 + 3 |
| Ассоциативность | (2 + 3) + 4 = 2 + (3 + 4) |
| Существование нейтрального элемента | 3 + 0 = 3 |
| Обратимость | 3 + (-3) = 0 |
Используя свойства сложения, мы можем вычислять сумму любого количества чисел. Для этого нам нужно сложить числа попарно, начиная с первого и продвигаясь поочередно к следующим числам. Например, чтобы вычислить сумму чисел 2, 5 и 7, мы можем сначала сложить 2 и 5, а затем прибавить 7 к полученной сумме. Получим: 2 + 5 + 7 = (2 + 5) + 7 = 7 + 7 = 14.
Сложение чисел на координатном луче
Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:
Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:
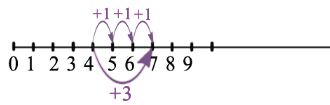
И мы попадем в точку 7, следовательно 4+3=7.
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :
Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:
В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство
От перестановки слагаемых сумма не меняется
Рассмотрим с помощью координатного луча следующие суммы: и , для этого от точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:
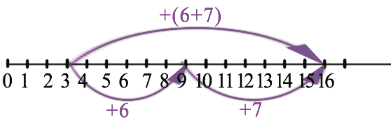
Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:
Мы получили второе свойство сложения — сочетательное свойство:
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:
Так как нам необходимо отложить от точки 0 единичных отрезков, то мы попадаем снова в ту же точку,т.е. значение числа от прибавления к нему нуля не изменилось: 7+0=7 . Применив переместительное свойство получим: 7+0=0+7=7, отсюда получаем третье свойство сложения — свойство нуля:
Если прибавить к нулю какое-нибудь число, то получится прибавленное число
Правило коммутативности
Одно из основных правил сложения чисел – это правило коммутативности. Оно устанавливает, что порядок слагаемых не влияет на результат сложения.
Формулировка правила коммутативности звучит следующим образом: для любых чисел a и b выполняется равенство a + b = b + a.
Пример: 2 + 3 = 3 + 2
Исходя из правила коммутативности, можно утверждать, что перестановка слагаемых в сумме не меняет ее значения. Например, если мы складываем числа 2 и 3, то результат будет одинаковым, независимо от того, какой порядок мы выберем: 2 + 3 = 3 + 2 = 5.
Правило коммутативности является одним из основных свойств сложения чисел и используется в множестве математических доказательств и операций. Оно позволяет упростить вычисления и облегчить понимание процесса сложения.
Презентация на тему: » 3 класс маршрут-справочник 1-я четверть. Вычисления в 3 классе Устные вычисления Повторение Вычисления в пределах 100 с переходом через десяток Новое.» — Транскрипт:
1
3 класс маршрут-справочник 1-я четверть

2
Вычисления в 3 классе Устные вычисления Повторение Вычисления в пределах 100 с переходом через десяток Новое Знакомство с числами больше 100 Простые вычисления в пределах 1000 Письменные вычисления Новое сложение в пределах Вычитание в пределах 1000 Умножение трехзначных чисел на однозначное число Деление трехзначных на однозначное (простые случаи) 1-е полугодие 2-е полугодие

3
Знакомство с трехзначными числами Последовательность чисел Принцип десятичного строения системы чисел Сложение и вычитание на основе последовательности чисел
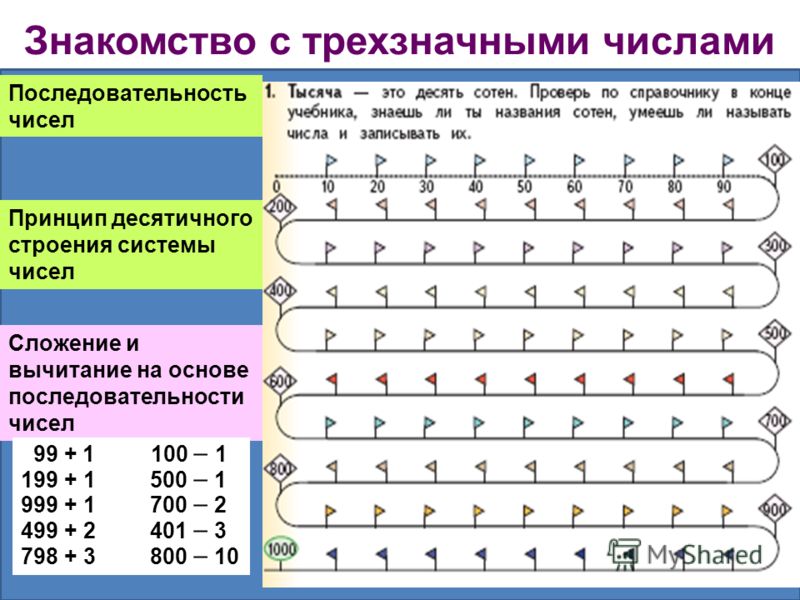
4
Знакомство с трехзначными числами Разрядный состав Сложение и вычитание на основе разрядного состава

5
Наглядность (цветовые ассоциации) Опоры при вычислениях цветовая маркировка = разрядная сетка 200 ? Сложение и вычитание по разрядам СДЕд
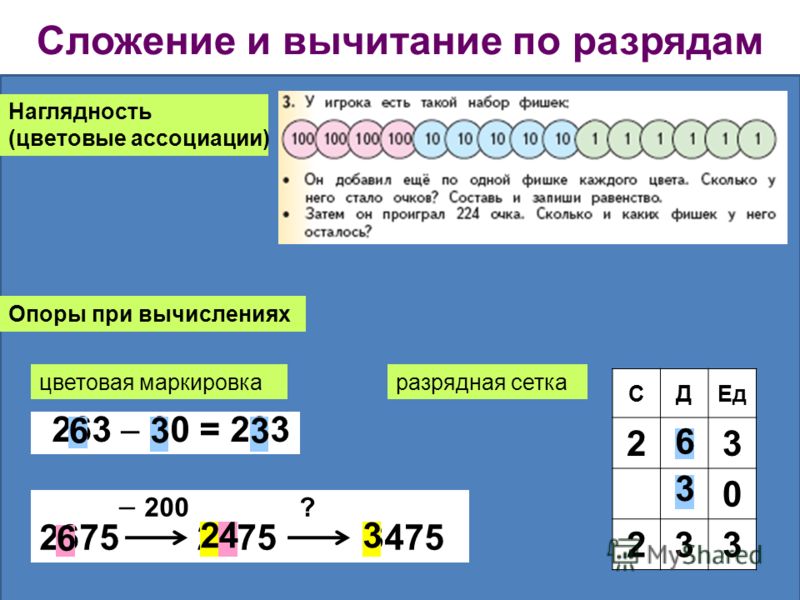
6
Сложение и вычитание по разрядам Вычисления по аналогии Сложение и вычитание сотен Прибавление и вычитание однозначного числа с переходом через десяток Сложение и вычитание десятков с переходом через сотню
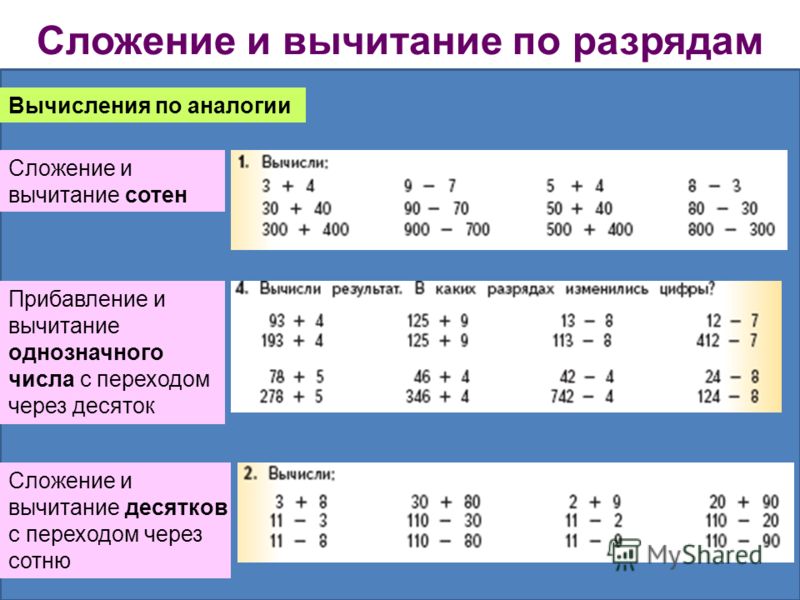
7
Проверка и тренинг

8
Итоги темы «Сложение и вычитание» Знакомство с приемами устных вычислений , Сложение и вычитание на основе последовательности чисел , Сложение и вычитание на основе разрядного состава , Сложение и вычитание по разрядам , Сложение и вычитание десятков с переходом через сотню Отработка этих вычислительных приемов в течение всей 1-й четверти

9
Умножение и деление СДЕд Повторение таблицы умножения Вычисления по аналогии Умножение и деление круглых чисел на однозначное
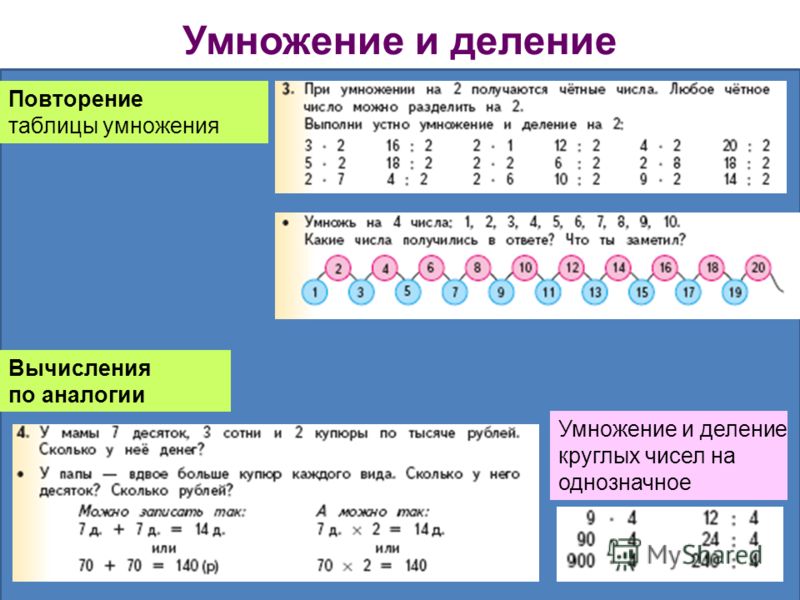
10
Вспомогательные приемы запоминания При умножении на 2, 4, 6, 8 получаются только четные числа Знакомство с простыми числами Вывод: простые числа нечетны, они не встречаются в таблице умножения
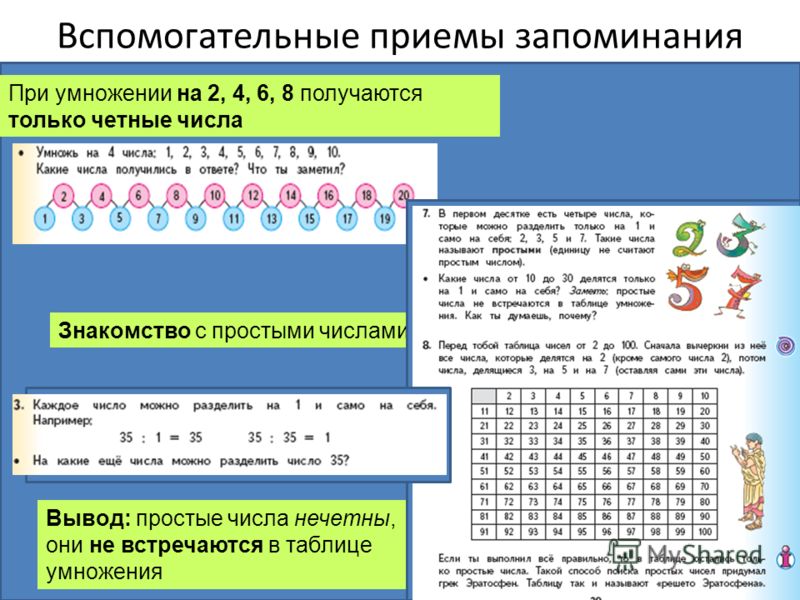
11
3 класс маршрут-справочник 2-я четверть
12
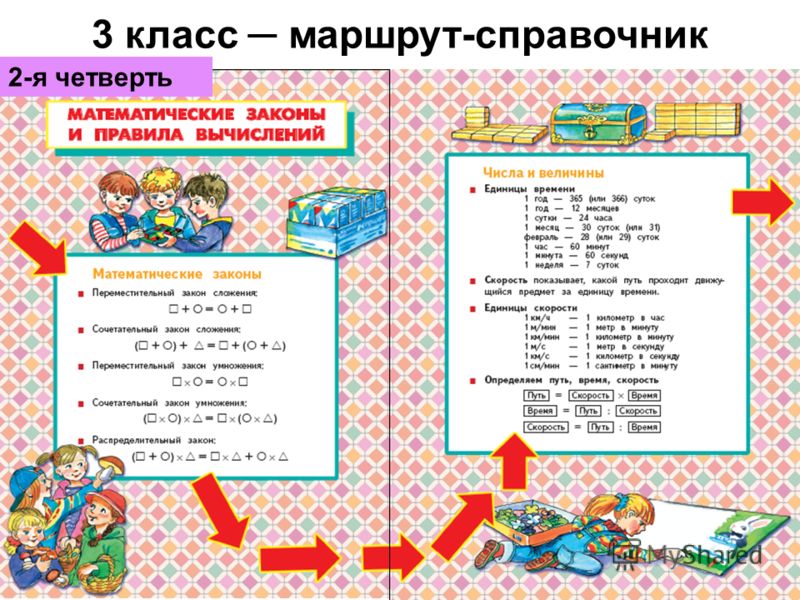
Устные вычисления ОТРАБОТКА Сложение и вычитание по разрядам Сложение и вычитание десятков с переходом через сотню Умножение и деление круглых чисел на однозначные НОВОЕ Сложение двузначных чисел с переходом через сотню Умножение и деление на 10, 100, 1000 Умножение круглых чисел Умножение и деление двузначного числа на однозначное Решение простых уравнений (неизвестное слагаемое, неизвестный множитель) 2-я четверть

13
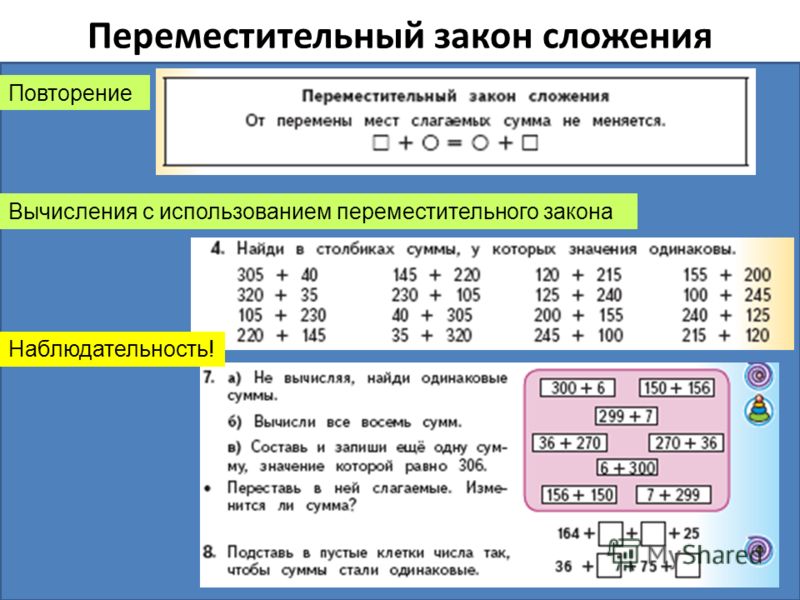
Переместительный закон сложения Повторение Вычисления с использованием переместительного закона Наблюдательность!
14
Переместительный закон умножения Повторение Нахождение неизвестного слагаемого Нахождение Неизвестного множителя

15
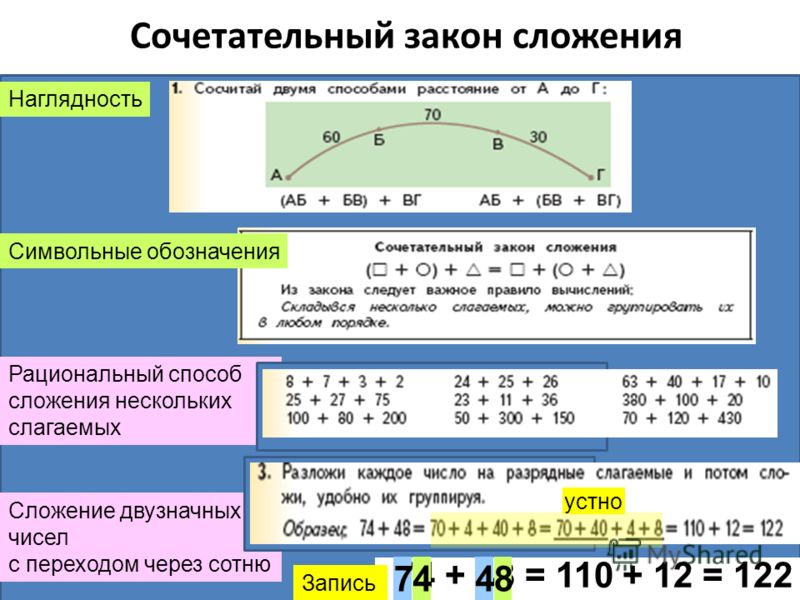
Сочетательный закон сложения Наглядность Сложение двузначных чисел с переходом через сотню Рациональный способ сложения нескольких слагаемых Символьные обозначения = = 122 Запись устно 7448
16
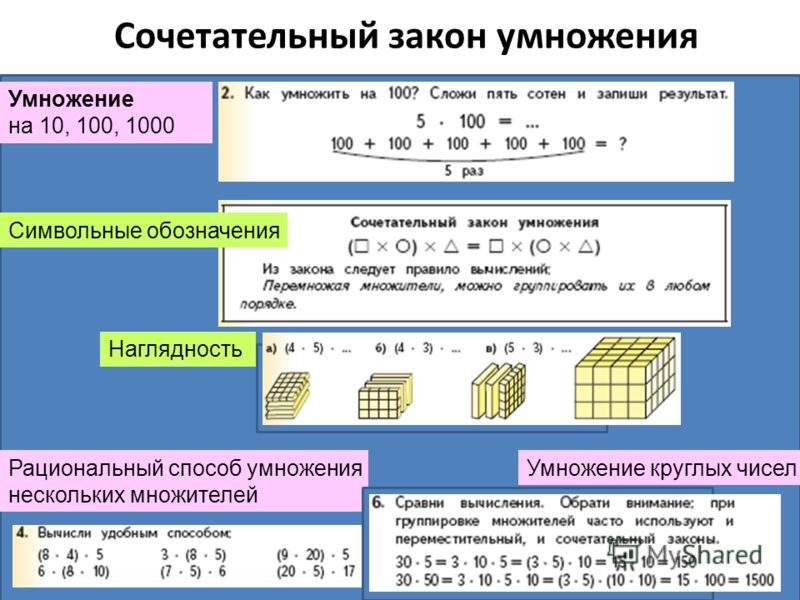
Сочетательный закон умножения Умножение на 10, 100, 1000 Умножение круглых чиселРациональный способ умножения нескольких множителей Символьные обозначения Наглядность
17
Проверка и тренинг Повторение Усложнение Новое

18
Распределительный закон Наглядность Рациональный способ вычисления
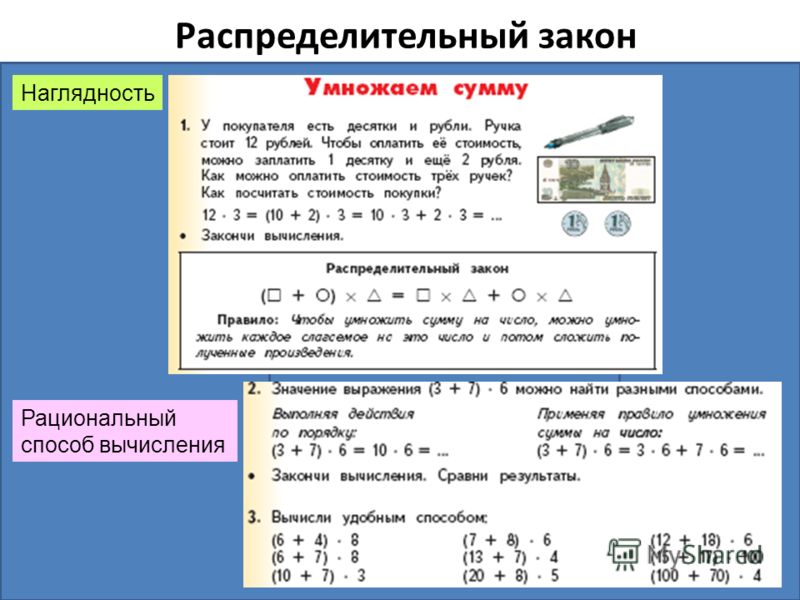
19
Умножение на однозначное число устно Наглядность Умножение двузначного числа на однозначное 18 · 3 = = 54 Запись устно

20
Деление на однозначное число Наглядность Разбиение на подходящие слагаемые Деление двузначного числа Применение правила устно
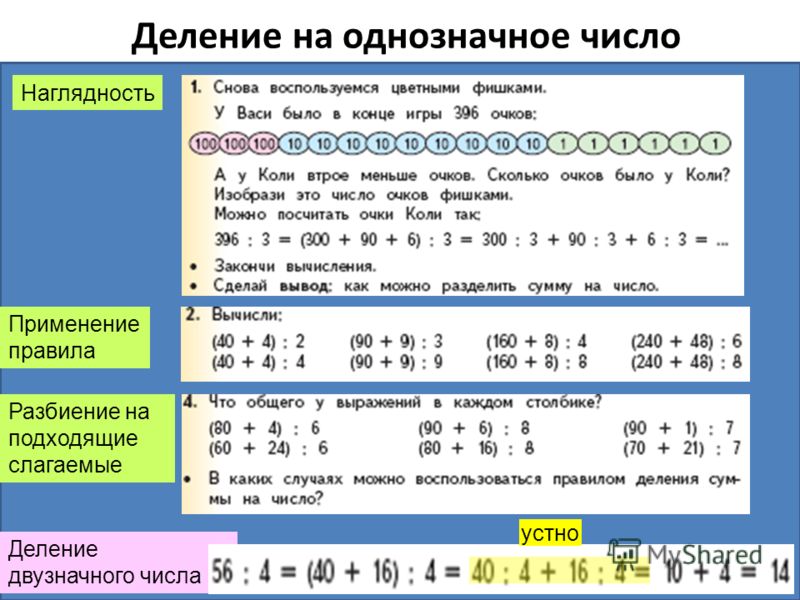
21
Осознанное выполнение вычислений Повторение Выбор способа вычислений Сравнение способов вычислений
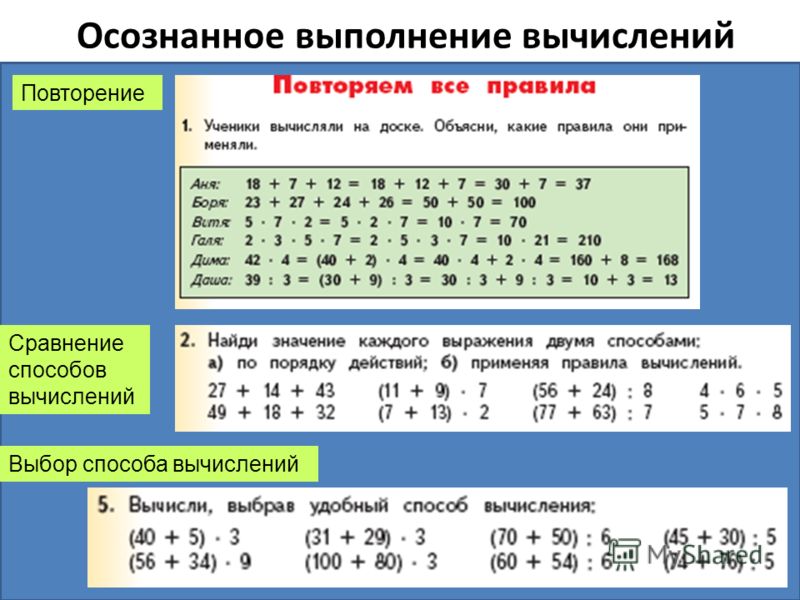
22
Итоги Высокая готовность к освоению алгоритмов письменных вычислений Сформированные представления о разрядном строении трехзначных чисел Сформированные представления о сложении и вычитании чисел по разрядам Сформированные представления об умножении чисел по разрядам Навыки устных вычислений

Сравнение натуральных чисел
читать материал украинским языком
При сравнении двух натуральных чисел возможны три варианта:
- число А больше числа В: А > B;
- число А меньше числа В: А < В;
- число А равно числу В: А=В.
Тут все предельно просто — два натуральных числа сравниваются поразрядно, начиная с самого старшего разряда.
Например:
- 273 > 199 — у первого числа в разряде сотен стоит 2, у второго 1, поскольку 2 больше 1, то первое число больше второго;
- 3 < 11 — из двух чисел всегда будет большим то, в написании которого используется больше цифр; можно поступить по-другому — дописать на место недостающих разрядов одного из чисел нули, т. е., надо сравнивать 03 и 11, поскольку 0 меньше 1, то первое число будет меньше второго.
Свойства сложения
-
Переместительное свойство (коммутативность):
При перестановке слагаемых сумма не меняется
$1 + 5 = 5 + 1 = 6.$
В общем виде переместительное свойство записывается так:
$a + b = b + a$.
-
Сочетательное свойство (ассоциативность):
Сумма трех и более слагаемых не изменится, если изменить порядок их сложения
$2 + ( 8 + 3 ) = ( 2 + 8 ) + 3 = 13.$
В общем виде сочетательное свойство записывается так:
$a + ( b + c ) = ( a + b ) + c.$
-
Свойство прибавления нуля:
Если к числу прибавить нуль, то сумма будет равна самому числу
$7 + 0 = 7.$
К этому свойству можно применить переместительное свойство, получим:
Если к нулю прибавить число, то сумма будет равна прибавляемому числу
$0 + 7 = 7.$
В общем виде:
$a + 0 = 0 + a = a.$
Если точкой $C$ разделить отрезок $AB$, то сумма длин отрезков $AC$ и $CB$ будет равна длине отрезка $AB$.
Рисунок 2.
Записывается: $AB = AC + CB$.
Сложение чисел можно удобно выполнять «в столбик»:
Рисунок 3.
Статья: Сложение и вычитание натуральных чисел
Найди решение своей задачи среди 1 000 000 ответов
Применение свойства сложения в алгебре
Применение свойства сложения облегчает вычисления суммы нескольких чисел. Если необходимо найти сумму трех или более чисел, можно сложить любые два числа в любом порядке, а затем полученную сумму добавить к оставшимся числам. Это позволяет существенно упростить вычисления и сократить количество операций.
| Пример вычисления суммы трех чисел: | Вычисления с использованием свойства сложения: |
|---|---|
| 5 + 7 + 3 | (5 + 7) + 3 = 12 + 3 = 15 |
| 7 + 5 + 3 | (7 + 5) + 3 = 12 + 3 = 15 |
| 3 + 5 + 7 | (3 + 5) + 7 = 8 + 7 = 15 |
В приведенном примере вычисления суммы трех чисел можно провести, меняя порядок слагаемых, и в результате во всех случаях получится одинаковая сумма. Это возможно благодаря свойству сложения.
Применение свойства сложения также распространяется на более сложные выражения, где есть как числа, так и переменные. В этом случае можно свободно менять порядок слагаемых и скобок без изменения результата.
Вычитание натуральных чисел
Вычитание — операция, обратная сложению.
Пример 2
На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?
Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:
$x + 3 = 7.$
Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.
Для этого используется вычитание:
$x = 7 — 3 = 4$, т.к. $3 + 4 = 7.$
Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым. Результат вычитания называется разностью.
Из данной задачи получаем:
$7$ — уменьшаемое, $3$ — вычитаемое, $8$ — разность.
В общем виде
Если $b + c = a$, то
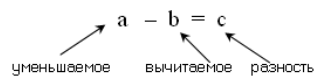 Рисунок 4.
Рисунок 4.
При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:
$11 — 3 = 8; 8 > 3.$
Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:
$11$ больше $3$ на $8$.
Переместительное и сочетательное свойства сложения
Ребята, запомним свойства сложения! С их помощью вычислять получается гораздо быстрее и легче.
Эти свойства показывают, что мы можем переставлять слагаемые, как удобно, а значит, позволяют упрощать вычисления.

7 + 9 + 3 + 1 + 8 + 6 + 2 + 4 + 3
16 + 12 + 4 + 8
Будем использовать оба свойства. Можно складывать в любом порядке.
Посмотрите внимательно на примеры! Какие два числа в сумме дают круглое число? Соединим их дугой. Внизу под дугой подпишем результат.

Решите самостоятельно примеры. Соединяйте дугой слагаемые (так удобнее и быстрее):
21 + 3 + 9 + 37
13 + 4 + 34 + 6 + 7

Есть другой способ записи: с использованием скобок.
Решим еще несколько примеров. Вычислим устно удобным способом следующие суммы:
20 + 8 + 40 + 2 = (20 + 40) + (8 + 2) = 60 + 10 = 70
30 + 1 + 9 + 60 = (30 + 60) + (1 + 9) = 90 + 10 = 100

Свойство сложения нуля и натурального числа, свойство сложения нуля с нулем.
Мы знаем, что нуль НЕ является натуральным числом. Так почему же мы решили рассмотреть свойство сложения нуля и натурального числа в этой статье? На это есть три причины. Первая: это свойство используется при сложении натуральных чисел столбиком. Вторая: это свойство используется при вычитании натуральных чисел. Третья: если считать, что нуль означает отсутствие чего-либо, то смысл сложения нуля и натурального числа совпадает со .
Проведем рассуждения, которые помогут нам сформулировать свойство сложения нуля и натурального числа. Представим, что в ящике нет ни одного предмета (иными словами, в ящике находится предметов), и в него помещают a предметов, где a – любое натуральное число. То есть, сложили и a предметов. Понятно, что после этого действия в ящике стало a предметов. Следовательно, справедливо равенство 0+a=a.
Аналогично, если в ящике находится a предметов и в него добавляют предметов (то есть, не добавляют ни одного предмета), то после этого действия в ящике окажутся a предметов. Таким образом, a+0=a.
Теперь мы можем привести формулировку свойства сложения нуля и натурального числа: сумма двух чисел, одно из которых равно нулю, равна второму числу. Математически это свойство можно записать в виде следующего равенства: 0+a=a или a+0=a, где a – произвольное натуральное число.
Отдельно обратим внимание на то, что при сложении натурального числа и нуля остается верным переместительное свойство сложения, то есть, a+0=0+a.
Наконец, сформулируем свойство сложения нуля с нулем (оно достаточно очевидно и не нуждается в дополнительных комментариях): сумма двух чисел, каждое из которых равно нулю, равна нулю. То есть, 0+0=0.
Теперь пришло время разобраться с тем, как выполняется сложение натуральных чисел.
Список литературы.
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Что такое натуральные числа
Много ситуаций вокруг нас связано с действиями с натуральными числами. Каждое из них можно представить шагами на обычной школьной линейке с нанесенными делениями, числовой прямой и координатном луче. В результате сложения исходное натуральное число увеличивается, а в результате вычитания — уменьшается. Для таких математических действий также существуют законы, которые будут рассмотрены ниже.
Понятие натурального числа обусловлено необходимостью естественного счета предметов и расположения цифр друг относительно друга. Множество таких чисел характеризуется бесконечностью. На деле это выглядит так: относительно любого числа есть еще одно, которое на единицу больше. Если расположить эти числа в порядке возрастания, получится натуральный ряд – еще одно математическое понятие, связанное с натуральными числами. Примером такого ряда является обычная линейка. В то же время необходимо понимать, что линейка имеет последнее число (например, линейка на 30 см ограничивается числом 30, а на 40 см — 40). В отличие от обычной линейки, числовая прямая не имеет крайнего числа, как показано на рисунке:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Представляя натуральные числа в виде числовой прямой, необходимо также помнить, что натуральным рядом является только множество целых чисел, причем имеющих знак «+». Если на прямой нанесены числа, расположенные слева от нуля, то этот ряд не является натуральным. Поэтому в математике говорят о расположении натуральных чисел на луче.
Расположение чисел на луче помогает представить действия с натуральными числами:
- продвинувшись на несколько делений вправо, число получает увеличение на число таких шагов;
- если переместиться на несколько шагов влево, получается результат, равный действию вычитания из исходного числа количества геометрических шагов.
Примечание 1
Геометрическим шагом называется единица, на которую совершается геометрическое действие.
На данном рисунке шагом является любой отрезок между двумя соседними натуральными числами.
Все натуральные числа можно назвать их множеством. Для обозначения такого множества определена буква латинского алфавита N.
В математике для множества натуральных чисел существуют следующие правила:
- Единица является наименьшим натуральным числом.
- При фоне существования наименьшего числа отсутствует наибольшее.
- При сравнении каждого последующего числа с предыдущим, обязательное условие — их разница на единицу. Другими словами, каждый последующий участник ряда больше предыдущего на один.
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15)<(34+54).
Бывают случаи, когда нельзя однозначно сказать, какая сумма больше. Например сравним суммы: (26+33) и (18+43), мы видим, что первое слагаемое первой суммы больше первого слагаемого второй суммы, но второе слагаемое первой суммы меньше второго слагаемого второй суммы. В таком случае необходимо наши суммы привести к виду первого примера, т.е. 26=18+8, следовательно, 26+33=(18+8)+33=18+8+33=18+41, теперь мы сравниваем (18+41) и (18+43), первые слагаемые равны, а 41<43, следовательно(18+41)<(18+43) и мы можем сказать, что (26+33)<(18+43).
Из выше сказанного, делаем вывод: При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.
Пример решения
Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:

- Пишется пример: 4+9+6+5+1+15+17+2+12+1.
- Переместительное свойство: 4+6+9+1+5+15+17+2+12+1.
- Сочетательный закон: (4+6)+(9+1)+(5+15)+(17+2+1)+12.
- Вычисление значений: 10+10+20+20+12=60+12=72.
Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.
Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.
Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Необычные приемы сложения: трюки и хитрости
На уроках математики в 5 классе вы учились складывать числа по правилам сложения. Однако, помимо основных правил, существуют и необычные приемы сложения, которые могут быть полезными при выполнении задач и в повседневной жизни.
Перенос единицы в уме
Если при сложении двух чисел получается число больше 9, необходимо обратить внимание на единицу в разряде десятков. Эта единица может быть перенесена в разряд единиц и прибавлена к числу в этом разряде
Например, при сложении 68 и 57, получается 125. Здесь единица из разряда десятков (6) переносится в разряд единиц и прибавляется к числу 5, получается число 12. Таким образом, верный результат сложения будет 125.
Умение складывать десятки
Для сложения двух чисел, в которых одно или оба числа оканчиваются на ноль, можно использовать прием сложения десятков. Например, при сложении 40 и 30, можно сразу прибавить 4 и 3, получается число 7, а потом добавить ноль в конце. Таким образом, верный результат сложения будет 70.
Суммирование чисел с одинаковыми разрядами
Если в сумме двух чисел все разряды совпадают (например, сложение 23 и 27), результат сложения можно получить следующим образом: сложить единицы (3+7=10), запомнить единицу и написать 0, а десятки оставить без изменения (2). Таким образом, результат сложения будет 50.
Сложение чисел по столбикам
Один из наиболее часто используемых приемов сложения — сложение чисел по столбикам. Для этого необходимо расположить числа одно под другим, выровнивая разряды, и сложить числа в каждом разряде по отдельности. В результате получается сумма чисел. Например, при сложении чисел 35 и 48 результат будет следующим:
| 3 | 5 | |
| + | 4 | 8 |
| —- | ||
| 8 | 3 |
Таким образом, результат сложения чисел 35 и 48 будет 83.
Знание этих необычных приемов сложения поможет вам быстрее и легче выполнять задачи по сложению и сделает процесс вычислений более интересным и разнообразным!

























