Среднее арифметическое

Физический смысл средней арифметической

Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.

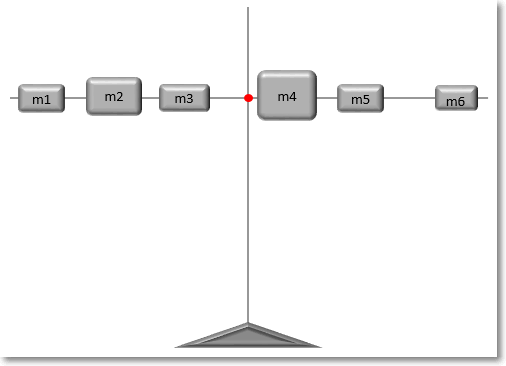
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (m_i), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.

И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.

Понятие среднего арифметического

К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?

Ответ на вопрос, можно получить двумя способами. Рассмотрим их.

1 

Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.

Разделим конфеты между детьми:

18 : 3 = 6.

Теперь известно, что каждому ребенку досталось 6 конфет.

Разделим шоколадки:

6 :3 = 2.

Каждой внучке досталось две шоколадки.

Разделим шоколадные яйца:

6 : 3 = 2.

Выяснили, бабушка привезла по два киндер-сюрприза.

Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:

6+2+2=10.

Получается, бабушка привезла по 10 сладостей.

Запишем решение задачи.

Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.

2

Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть.  Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:

Среднее арифметическое нескольких чисел — результат деления суммы этих чисел на их количество

Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:

18+6+6=30.

Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:

30 : 3 =10.

Каждой внучке досталось по 10 сладостей.

Запишем решение этой задачи с использованием второго способа.

Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!

Семплирование

Предположим, вам требуется решить важную задачу: выяснить среднюю ширину морды домашних котов нашей страны. Прямой способ, то есть измерение всех домашних питомцев, невозможен по ряду объективных причин. Придётся ограничиться выборкой — взять какое-то число животных, измерить морды именно им и сделать выводы по итогам только этих исследований.

Иллюстрация: Pixabay

Но тут сразу же возникают вопросы:

• Сколько и каких котов отобрать для замера?
• Почему именно этих, а не других?
• Какие есть гарантии, что вычисленное значение действительно будет средней шириной морды всех котов России?

Семплирование — это группа статистических методов и приёмов, отвечающих на эти вопросы. С помощью семплирования мы формируем нашу выборку так, чтобы она наилучшим образом отражала свойства генеральной совокупности — то есть свойства всех котов страны.

Качественная выборка сохраняет свойства всей генеральной совокупности

Иными словами, вы не можете измерить N первых попавшихся котов и обобщить результат для остальных. Выборка должна хорошо «сидеть» во всей популяции кошек, чтобы можно было делать обоснованные выводы. Такую выборку называют релевантной.

Кстати, статистика и котики — близнецы-братья. После выхода одноимённой книги Владимира Савельева мы говорим «статистика», а подразумеваем «котики», и наоборот. И смело рекомендуем эту книгу всем, кто дочитал до этого места.

В Data Science методы семплирования применяются при разработке, подготовке и оценке датасетов, чтобы они одновременно и были упорядоченными, и соответствовали реальности.

Средняя арифметическая взвешенная

Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч. 

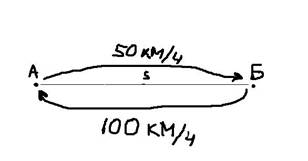
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

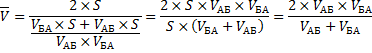
Подставим значения.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую. 

Средняя арифметическая как оценка математического ожидания

Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.

Формула матожидания имеет следующий вид:

где M(X) – математическое ожидание

x_i – это случайные величины

p_i – их вероятности.

То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.

Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.

Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.

Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.

где x_i – значения переменной,n – количество значений.

Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений). 

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

66,2 × 3 = 198,6 км.

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

78,4 × 2 = 156,8 км.

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Примеры расчета среднего арифметического

Пример 1. Вычислить среднее арифметическое от 33,3 и 55,5.

Как мы решаем:

Чтобы найти среднее арифметическое двух чисел, сложите эти числа и разделите результат на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Пример 2. Вычислить среднее арифметическое 7,5 и 8 и 0,5.

Как мы решаем:

Чтобы найти среднее арифметическое трех чисел, сложите эти числа и разделите результат на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.

Пример 3. Найдите среднее арифметическое 202, 105, 67 и 9.

Как мы решаем:

Чтобы найти среднее арифметическое четырех чисел, сложите эти числа и разделите результат на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.

Пример 4. Сколько денег в среднем тратит студент в неделю, если в понедельник он потратил 80 руб., во вторник — 75 руб., в среду и четверг — 100 руб., в пятницу — 50 руб.

Как мы решаем:

Чтобы найти, сколько средний студент потратил за пять дней, сложите эти суммы и разделите результат на 5: (80 + 75 + 100 + 100 + 50): 5 = 405: 5 = 81.

Ответ: студент тратит в среднем 81 рубль в неделю.

Подсчёт среднего арифметического пары

Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:

1. Первоначально требуется провести операцию сложения выбранных чисел. Это часто можно сделать, как говорится, вручную, не используя электронную технику.
2. После того как сложение произведено и получен его результат необходимо произвести деление. Данная операция подразумевает разделение суммы двух сложенных чисел на два – количество сложенных чисел. Именно такое действие и позволит получить требуемую величину.

Формула

Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:

(А+В)/2

В этой формуле применяется следующее обозначение:

А и В – это заранее выбранные числа, для которых необходимо находить значение.

Смещение

Аналогично тому, как производится выборка из генеральной совокупности, дата-сайентисты из готового датасета выделяют тренировочный набор. Именно на этой «выборке второго порядка» модель учится делать предсказания.

Прочитайте нашу статью о создании простой модели машинного обучения. Она предсказывает город, в который вероятнее всего поедет турист, на основании его возраста, пола, места жительства, дохода и транспортных предпочтений. Такая рекомендательная система на минималках.

Смещение происходит, когда модель недооценивает или переоценивает какой-либо параметр. Представим, что модель из статьи выше отправляет всех краснодарцев в Париж — независимо от их дохода, предпочтений и других параметров. В этом случае мы скажем, что модель переоценивает значение параметра «Город проживания».

Чаще всего причиной смещения являются:

• неправильный сбор данных в датасет: например, в него попали только краснодарцы — любители Парижа;
• неправильное формирование тренировочного набора из датасета;
• неправильное измерение ошибок.

Когда мы неверно собираем данные, говорят о систематической ошибке отбора. Например, в прошлом веке многие считали, что во Вселенной больше голубых галактик, — впечатление возникало потому, что плёнка была более чувствительна к голубой части спектра.

О доброте дельфинов мы знаем только от спасённых ими людей. Фото: Pixabay

Другая ошибка — ошибка меткого стрелка — происходит, когда мы вольно или невольно отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадём.

Причин, вызывающих смещение, так много, что Марк Твен заметил: «Существует три вида лжи: ложь, наглая ложь и статистика». Например:

• Эффект низкой/высокой базы. Если в финансовом отчёте найти самый низкий показатель прибыли, то на его фоне любой другой результат будет выглядеть как достижение. И наоборот: если хотите показать, что ученик перестал прогрессировать, сравнивайте текущие оценки с его лучшими результатами за все годы обучения.
• Сокращение рассматриваемого периода. Если хочется доказать, что рекламная кампания не приносит результатов, надо просто найти период, когда деньги уже потрачены, а эффекта ещё нет. И рассматривать только его.
• Исключение из выборки. Если вы измеряете результативность методики снижения веса, то можно выкидывать из выборки участников, которые отказались от методики, не дойдя до конца. Это существенно «повысит» эффективность методики.
• Ну и, конечно же, классика: «Интернет-опрос населения показал, что 100% населения пользуются интернетом».

Эти и другие ошибки смещения трудно выявить статистическими методами, поэтому нужно стараться избежать их до того, как вы начнёте сбор данных.

Если пить «Боржоми» уже поздно (датасет уже сформирован), обязательно спросите себя: «Не смещены ли мои данные?» — а они наверняка смещены, «Куда и почему они смещены?» и «Можно ли с этим жить?»

Конспект

Математика – 5, тема: «Среднее арифметическое»
Ковалева Оксана Александровна. ГБОУ ООШ № 2 г.Октябрьск, Самарская область.

Среднее арифметическое.

Цель урока:

Познакомить учащихся с понятиями «среднее арифметическое», «средняя скорость».

Научить учащихся находить среднее арифметическое нескольких чисел, применять эти знания при решении задач.

Научить учащихся находить среднюю скорость движения, применять эти знания при решении задач.

Оборудование: Компьютер, проектор.

Ход урока.

Урок построен на презентации, которая рассчитана на все занятие.

I. Постановка проблемы (слайд № 2).

II. Учащимся дается понятие «среднее арифметическое нескольких чисел» и алгоритм его нахождения (слайды № 3 – 7).

После этого идет закрепление понятия (слайды № 8 – 11). При решении ученики повторяют перевод длины из сантиметров в метры и наоборот.

III. Учащимся на примере оценивания спортивных соревнований, дается представление о практическом применении среднего арифметического (слайд № 12).

IV. Дается правило и закрепление материала «нахождение средней скорости движения» (слайд № 13 – 14).

V. Закрепление материала урока (слайды № 15 – 17) проходит в форме решения задач повышенной сложности. Задачи слайдов № 17 – 18 взяты с сайта www.math-on-line.com.

VI. Закрепление теории (слайды № 18 – 22).

VI. Итоги урока. Домашнее задание.

Используемая литература и Интернет-источники.

Виленкин Н. и др. «Математика – 5», «Мнемозина», М,. 2004, стр. 312 – 318.

2. www.math-on-line.com – олимпиады, игры, конкурсы по математике для школьников.

Математика – 5, тема: «Среднее арифметическое»
Ковалева Оксана Александровна. ГБОУ ООШ № 2 г.Октябрьск, Самарская область.

Среднее арифметическое.

Цель урока:

Познакомить учащихся с понятиями «среднее арифметическое», «средняя скорость».

Научить учащихся находить среднее арифметическое нескольких чисел, применять эти знания при решении задач.

Научить учащихся находить среднюю скорость движения, применять эти знания при решении задач.

Оборудование: Компьютер, проектор.

Ход урока.

Урок построен на презентации, которая рассчитана на все занятие.

I. Постановка проблемы (слайд № 2).

II. Учащимся дается понятие «среднее арифметическое нескольких чисел» и алгоритм его нахождения (слайды № 3 – 7).

После этого идет закрепление понятия (слайды № 8 – 11). При решении ученики повторяют перевод длины из сантиметров в метры и наоборот.

III. Учащимся на примере оценивания спортивных соревнований, дается представление о практическом применении среднего арифметического (слайд № 12).

IV. Дается правило и закрепление материала «нахождение средней скорости движения» (слайд № 13 – 14).

V. Закрепление материала урока (слайды № 15 – 17) проходит в форме решения задач повышенной сложности. Задачи слайдов № 17 – 18 взяты с сайта www.math-on-line.com.

VI. Закрепление теории (слайды № 18 – 22).

VI. Итоги урока. Домашнее задание.

Используемая литература и Интернет-источники.

Виленкин Н. и др. «Математика – 5», «Мнемозина», М,. 2004, стр. 312 – 318.

2. www.math-on-line.com – олимпиады, игры, конкурсы по математике для школьников.

Пример решения

Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.

Решение выполняется по следующему алгоритму:

1. Записать величины: 3 2/3, 4 5/7 и 6 3/8.
2. Количество: 3.
3. Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.
4. Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.
5. Вычислить сумму: 2479/168.
6. Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.
7. Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.
8. Значение искомой величины равно 4 463/504.

При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.

Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.

Свойства среднего арифметического

Среднее арифметическое имеет следующие характеристики:

Сумма отклонений всех данных в распределении от среднего значения равна нулю.

Если мы добавим одинаковую сумму ко всем данным в выборке, среднее значение выборки увеличится на эту сумму.

То же самое происходит и с умножением: если все значения выборки умножить на число, среднее значение выборки умножится на это число.

Среднее арифметическое можно вычислить только в количественных переменных . Другими словами, вы не можете взять среднее значение качественных переменных.

Среднее арифметическое всегда будет значением между минимумом и максимумом распределения.

Этот тип среднего значения очень чувствителен к очень высоким или очень низким значениям, в результате чего выброс существенно меняет результат среднего арифметического.

Среднее арифметическое набора данных всегда равно или больше среднего геометрического того же набора данных.

Среднее арифметическое для сгруппированных данных

Под сгруппированными данными мы подразумеваем, что данные структурированы в виде групп или интервалов. Обычно это происходит, когда размер статистической выборки очень велик.

Таким образом, вычисление среднего арифметического немного меняется, когда данные сгруппированы вместе, хотя концепция та же самая.

Чтобы вычислить среднее арифметическое данных, сгруппированных в интервалы, балл класса каждой группы необходимо умножить на ее абсолютную частоту, а затем разделить на сумму всех абсолютных частот.

Примечание. Оценка класса интервала рассчитывается путем деления суммы конечных точек интервала на два. Например, классная заметка интервала [3,7) будет такой:

Чтобы вы могли увидеть, как это делается, ниже приведено решенное упражнение на среднее арифметическое данных, сгруппированных по интервалам:

Мы хотим статистически изучить вес группы, для этого мы опросили репрезентативную группу из 81 человека и получили следующие данные:

Где x _i — классный балл каждой группы, а f _{i —} ее абсолютная частота, то есть количество людей, имеющих вес в этом интервале.

Чтобы определить среднее арифметическое, необходимо добавить в таблицу частот столбец, который представляет собой произведение примечаний к классу на соответствующие абсолютные частоты:

Таким образом, чтобы вычислить среднее арифметическое сгруппированных данных, просто разделите сумму произведений классных примечаний на их частоты на общее количество данных:

Задачи на нахождение среднего арифметического натуральных чисел

Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.

Сначала найдём сумму всех расстояний. У нас получится $30 \cdot 2 + 60 + 100 \cdot 3 = 420$

Теперь разделим эту сумму расстояний на количество часов.

$$420 : 6 = 70$$

Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.

Рассмотрим другую задачу.

Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?

Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.

$$38 \cdot 3 = 114$$

Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.

$$114-50-44 = 20$$

Показать проверку

Скрыть

$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$

{"questions":[{"content":"$23$ ученика писали контрольную работу. Пятеро написали на «$5$», тринадцать – на «$4$», остальные на «$3$». Каков средний балл по классу?`input-1`","widgets":{"input-1":{"type":"input","answer":"4"}},"step":1,"hints":["Сначала найдём число учеников, написавших работу на «$3$». Это нужно нам для нахождения суммы всех баллов. <br />$23-18 = 5$","Теперь вычисляем сумму баллов. Для этого каждую отметку умножаем на количество детей, которые её получили. <br />$5 \\cdot 5 + 4 \\cdot 13 + 3 \\cdot 5 = 25 + 52 + 15 = 92$","Теперь нужно полученную сумму разделить на количество учеников. Это и будет средний балл.<br />$92 : 23 = 4$"]}]}

Примеры задач

упражнение 1
У Пети было 4 яблока, у Даши — 6, а у Лены — 5. Они решили собрать все фрукты вместе и разделить их между собой поровну. Подсчитайте, сколько яблок достанется каждому.

Решение
В данном случае у нас есть три числа и нам нужно найти их среднее арифметическое. Для этого используйте приведенную выше формулу:

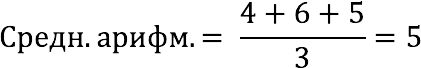
Ответ: Каждый имеет право на 5 яблок.

Задача 2
Спортсмен потратил 5 часов на преодоление расстояния от точки А до точки Б, при этом скорость была следующей: первые два часа — 6 км/ч, затем два часа — 9 км/ч, а последние 60 минут — 7 км/ч ч ч. Найдите свою среднюю скорость.

Решение
Итак, нам нужно вычислить среднее арифметическое пяти чисел, соответствующих скоростям на каждый час бега:

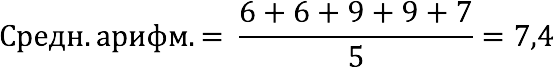
Ответ: Средняя скорость спортсмена 7,4 км/ч.

Как посчитать среднее арифметическое

Чтобы посчитать среднее арифметическое, нужно сложить все имеющиеся значения какой-либо величины и разделить на количество этих значений. Для четырёх значений $a, b, c, d$ среднее арифметическое равно

$\frac{a+b+c+d}{4}$.

Если же $a, b, c$ и $d$ заданы не в одной единице измерения, а, например, в метрах и сантиметрах, то сначала нужно выбрать общую единицу измерения и привести все значения к ней.

Пример 1

Эдуард прыгнул в длину $5$ раз. Первый раз он прыгнул на расстояние $173$ см, второй раз на $169$ см, третий раз на $1,7$ м, а четвёртый и пятый соответственно — на $168$ и $175$ см. Посчитайте, на какую длину в среднем прыгает Эдуард.

Решение:

Длина третьего прыжка Эдуарда дана в метрах, а остальные его результаты — в сантиметрах. Поэтому переведём длину третьего результата также в сантиметры. Для этого умножим метры на $100$, так как в одном метре содержится 100 сантиметров:

$l_3=1,7 м = 1,7 \cdot 100 см= 170$ см.

Теперь мы можем найти среднюю длину его прыжка:

$l_{ср.}=\frac{173+169+170+168+175}{5}=171$ см.

Ответ: В среднем Эдуард прыгает на длину в 171 см.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Полезные ссылки:

• SQL и теория вероятностей (YouTube)
• Анализ нормальности распределения данных (YouTube)
• Меры центральной тенденции

Роман Романчук

Эксперт по маркетинговой и продуктовой аналитике, ex-директор по аналитике Сравни.

• Как правильно организовать работу с гипотезами? — 21.11.2023
• Кейс: как построить отдел аналитики в большой компании? — 06.05.2022
• Учимся применять оконные функции — 29.09.2020

Заключение

Data Science — не просто комбинирование модных моделей в Jupyter-ноутбуке. Профессионалы в этой области глубоко понимают природу данных и то, как они могут помочь в принятии конкретных бизнес-решений.

Всё это изучалось в статистике задолго до того, как первый дата-сайентист набрал свой первый import pandas as pd. Статистика — фундамент всей современной науки о данных, включая машинное обучение, глубокие нейросети и даже искусственный интеллект.

В нашем курсе «Профессия Data Scientist» статистике уделено самое пристальное внимание. Вы не ударите в грязь лицом ни на тусовке статистиков, ни на настоящем DS-собеседовании

Приходите!