Логарифмические уравнения. как решать логарифмические уравнения?

Решение однородных логарифмических уравнений

В задачниках встречаются логарифмические уравнения, которые являются однородными уравнениями относительно некоторых логарифмов. Например, lg2(x+1)−lg(x+1)·lg(x−1)−2·lg2(x−1)=0 – это логарифмическое уравнение, однородное относительно логарифмов lg(x+1) и lg(x−1).

Решение однородных логарифмических уравнений завязано на преобразовании, заключающемся в делении обеих частей уравнения на «старшую» степень одного из логарифмов, что в дальнейшем позволяет ввести новую переменную. При этом необходимо отдельно проверять, не являются ли корнями уравнения те значения переменной, при которых обращается в нуль логарифм, на который планируется проводить деление. Давайте обратимся к конкретному примеру.

Возьмем наше уравнение lg2(x+1)−lg(x+1)·lg(x−1)−2·lg2(x−1)=0. Оно, как мы отметили, является однородным относительно логарифмов lg(x+1) и lg(x−1). Давайте разделим обе части этого уравнения на старшую степень второго из этих логарифмов, то есть, на lg2(x−1). Но, как известно, делить обе части уравнения мы имеем право только на выражение, не обращающееся в нуль, в противном случае можно потерять корни. Поэтому, стоит отдельно проверить, не являются ли корнями уравнения значения переменной, при которых lg2(x−1)=0, а уже после этого спокойно проводить задуманное деление, не опасаясь потерять корни. В нашем случае lg2(x−1)=0 только при x=2. Но x=2 не является решением исходного уравнения, так как его подстановка в исходное уравнение дает неверное числовое равенство. Теперь можно переходить к делению, считая lg2(x−1)≠0. Имеем:

Дальше напрашиваются следующие преобразования

Остается закончить решение, воспользовавшись методом введения новой переменной. Приняв , имеем

Откуда

Ответ: , 3.

40.500. Логарифмические уравнения

Логарифмом числа $ b $ по основанию $ a(c=log_{a}b) $ называется такой показатель степени $ c $, в которую нужно возвести $ a $, чтобы получить $ b $ (то есть $ a^{c}=b $). При этом задаются ограничения: $ a>0, \; a \neq 1, \; b>0$. Значение $ c $ логарифма может быть любым.

Вычислите:

$ log_{3}27, \; log_{\frac {1}{3}}27 $

1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.

$ 3=log_{3}27 $

2. При возведении $ \big(\frac{1}{3} \big)^{-3}=27 $ значит, $ -3=log_{\frac{1}{3}}27 $

Ответ: 3; -3.

Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.

Пусть $ y=log_{2}x $. Подставим вместо $ x $ разные числа и определим соответствующие значения переменной $ y $.

Отметим координаты точек на плоскости и соединим их плавной линией.

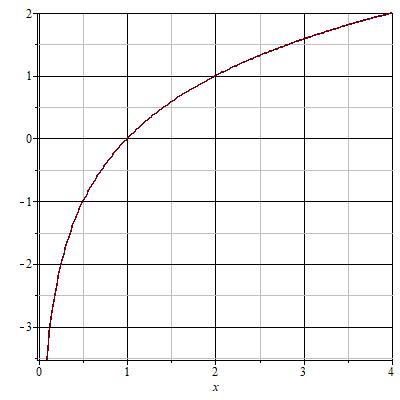
Легко заметить, что функция все время возрастает. Такое поведение характерно для всех логарифмических функций с основанием больше единицы.

Пусть теперь $ y=log_{\frac{1}{2}}x $. Составим таблицу значений для этого случая.

Тогда график функции будет выглядеть следующим образом.

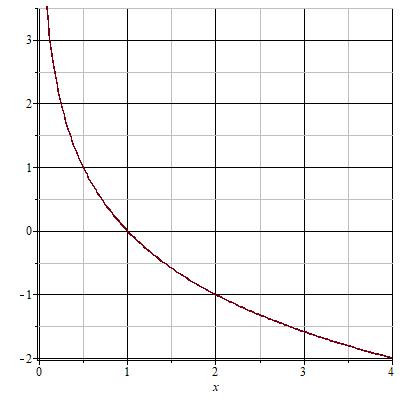
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.

Графики всех логарифмических функций проходят через точку с координатами (1;0).

Особыми знаками принято обозначать логарифмы с основанием десять $ log_{10}a=lga $ и логарифмы с натуральным основанием $ e \approx 2.72 \; log_{e} \; a=In \; a $.

Свойства логарифмов

Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.

Правило	Формула
Логарифм 1 по любому основанию равен 0.	$log_{a}1=0$
Логарифм числа по равному ему основанию равен 1.	$log_{a}a=1$
Основное логарифмическое тождество. При разведении основание в степень логарифма получается подлогарифмическое выражение.	$a^{log_{a}b}=b$
Логарифм произведения равен сумме логарифмов.	$log_{a}bc=log_{a}b+log_{a}c$

Логарифм частного равен разности логарифмов.	$log_{a} \frac{b}{c}=log_{a}b-log_{a}c$
Показатель степени можно выносить из подлогарифмического выражения за знак логарифма.	$log_{a}b^{p}=plog_{a}b$
Показатель степени можно выносить из основания логарифма, возводя его в -1 степень.	$log_{a^{a}}b=\frac{1}{q}log_{a}b$
Можно представить логарифмов в виде частного логарифмов с новым основанием.	$log_{a}b=\frac {log_{c}b}{log_{c}a}$
Если поменять местами подлогарифмическое выражение и основание логарифма, получится логарифм, обратный исходному.	$log_{a}b=\frac {1}{log_{b}a}$

Используем рассмотренные свойства для решения некоторых задач.

Пример 2

Вычислите $ log_{5}3125 $

1. Представим $ 3125=5^{5} $.

2. Вынесем степень из—под знака логарифма:

$ log_{5}3125=log_{5}5^{5}=5log_{5}5 $

3. Логарифм числа по равному ему основанию равен 1:

$ 5log_{5}5=5 $

Ответ: 5.

Пример 3

Вычислите $ 5^{2+log_{5}3} $

1. Воспользуемся свойством степеней:

$ 5^{2+log_{5}3}=5^{2} \cdot 5^{log_{5}3} $

2. Используем основное логарифмическое тождество:

$ 5^{2} \cdot 5^{log_{5}3}=25 \cdot 3=75 $

Ответ: 75.

Пример 4

Вычислите $ lg125+lg8 $

1. Воспользуемся формулой для суммы логарифмов:

$ lg125+lg8=lg1000 $

2. Представим 1000 = 103 и вынесем 3 за знак логарифма:

$ lg1000=lg10^{3}=3lg10 $

3. Воспользуемся тем, что $ lg10=1 $.

Ответ: 3.

Пример 5

Вычислить $ log_{36}84-log_{36}14 $.

1. Воспользуемся формулой для частного логарифмов:

$ log_{36}84-log_{36}14=log_{36}6 $

2. Преобразуем основание логарифма 36 = 62 и вынесем, «перевернув», вынесем показатель:

$ log_{36}6=log_{6^{2}}6= \frac {1}{2}log_{6}6 $

3. Воспользуемся тем, что $ log_{6}6=1 $

Ответ: 0,5.

Пример 6

Вычислите $ \frac {lg8+lg18}{2lg2+lg3} $.

1. Применим в числителе формулу для сумы логарифмов:

$ \frac {lg8+lg18}{2lg2+lg3}=\frac {lg144}{2lg2+lg3} $

2. В знаменателе внесем 2 под знак логарифма:

$ 2lg2=lg2^{2}=lg4 $

3. Воспользуемся формулой суммы логарифмов для знаменателя:

$ \frac {lg144}{lg4+lg3}=\frac {lg144}{lg12} $

4. Перейдем от частного к логарифму с основанием 12:

$ \frac {lg144}{lg12}=log_{12}144 $

5. Представим 144 = 122, вынесем степень за знак логарифма и воспользуемся соотношением $ log_{12}12=1 $

$ log_{12}144=log_{12}12^{2}=2log_{12}12=2 $

Ответ: 2.

Кроме выражений с числами, на экзамене могут встретиться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.

Пример 7

Вычислите $ log_{125}\frac {a^{2} \cdot a}{a^{3}} $

1. Преобразуем отдельно подлогарифмическое выражение:

$ \frac {a^{2} \cdot a}{a^{3}}=a^{2+1-3}=a^{0}=1 $

2. Логарифм 1 по любому основанию равен 0:

$ log_{125}1=0 $

Ответ: 0.

Прочитано
Отметь, если полностью прочитал текст

Вычисление уравнений с логарифмом

Пример 16.1 Решить уравнение log_ax=c.

А	Б	В	Г	Д
ø	a•c	ca	ac	c/a

Решение: Имеем простейшее логарифмическое уравнение, которое решается методом сведения к одному основанию логарифмов:log_ax=c (здесь a>0, a≠1),log_ax=c•1, log_ax=c•log_aa, log_ax= log_aac Здесь использовали свойства логарифма, единицу расписали как логарифм основания, после чего множитель c внесли под логарифм. Далее опустили основы и приравняли выражения в логарифмах:x=ac. ОДЗ: x>0. Ответ: ac – Г.

Пример 16.2 Решить уравнение log_1/2(x)=-4.

А	Б	В	Г	Д
ø	-16	1/16	1/16; 16	16

Решение: ОДЗ функции под логарифмом: x>0. Сводим уравнение к одному основанию логарифмов При равных основах приравниваем выражения под логарифмами:x=(1/2)-4, x=24, x=16. Ответ: 16 – Д.

Пример 16.3 Решить уравнение log₂(-x)=5.

А	Б	В	Г	Д
ø	32	-32	1/32	-1/32

Решение: Выполняем раскрытия логарифмов по данной в начале инструкции: ОДЗ – -x>0,x<0. Упростим уравненияlog₂(-x)=5 log₂(-x)=5•1 log₂(-x)=5• log₂2 log₂(-x)= log₂25 опустим основы и приравняем логарифмические выражения:-x=25, -x=32, x=-32. Ответ: -32 – У.

Пример 16.4 Решить уравнение lg(x2-x)=1-lg(5).

А	Б	В	Г	Д
ø	-3; 2	-2; 1	-2; 3	-1; 2

Решение: ОДЗ: x2-x>0, x(x-1)>0Решим неравенство методом интервалов x(x-1)=0, x₁=0, x₂=1. x∈(-∞;1)∪(1;+∞). На этом множестве значений и ищем решение уравнения, сперва сведя к одной основе логарифмы по теореме Виета:x₁+x₂=1, x₁•x₂=-2. x₁=-1, x₂=2. Оба корня принадлежат ОДЗ. Ответ: -1; 2 – Д.

ОДЗ неравенства могут быть сложнее, чем сами уравнения, тогда достаточно сами корни уравнения подставить в неравенство (или систему неравенств) и определить, принадлежат ли корни области допустимых значений логарифмческого уравнения.

Пример 16.5 Сколько корней имеет уравнение lg(x4-10×2)=lg₃x3?

А	Б	В	Г	Д
Ни одного	один	два	три	четыре

Решение: В логарифме имеем биквадратное выражение, которое при условиях на ОДЗ требует вычислений.Поэтому пойдем другим путем, сначала решим уравнение с логарифмом, а в конце проверим удовлетворяют ли найденные «иксы» ОДЗ: по теореме Виета:x₂+x₃=3 x₂•x₃=-10. x₂=-2 x₃=5. Проверим найденные значения 0; -2; 5 являются решениями. Выписываем ОДЗ и подставляем «иксы»: 1) 0=0, поэтому x₁=0 не принадлежит ОДЗ;

2) (-2)4-10•(-2)=16-40=-24<0 x₂=-2 не принадлежит ОДЗ.

3) 5^4-10•5^2=625-250=375>0,x₃=5 удовлетворяет ОДЗ. Логарифмическое уравнение lg(x^4-10x^2)=lg₃x3 имеет один корень. Ответ: один – Б.

Пример 16.6 Решить уравнение log₆(x-2)+log₆(x-1)=1 и указать промежуток, которому принадлежит его корень. Решение: Выпишем систему неровностей для ОДЗ: По правилу, что сумма логарифмов чисел равна логарифму их произведения ln(a)+ln(b)=ln(a•b) и свойству log₆6=1, сведем логарифмы к общему основанию: При преобразованиях получили квадратное уравнение, корни которого находим по теореме Виета:x₁+x₂=3 x₁•x₂=-4. x₁=-1<2 (не принадлежит ОДЗ)x₂=4.x=4 – единственный корень заданного уравнения, он принадлежит промежутку (3,9;4,1). Ответ: (3,9;4,1) – Б.

Пример 16.9 Решить уравнение (log₂x)2-2log₂x-3=0 и указать сумму его корней.Решение: ОДЗ: x>0. логарифмическое уравнение(log₂x)2-2log₂x-3=0 сведем к квадратному заменой log₂x=t.t2-2•t-3=0 По формулам Виета имеем: t₁+t₂=2 – сумма корней уравнения;t₁•t₂=3 – их произведение, тогда t₁=-1 и t₂=3 – корни квадратного уравнения. Возвращаемся к замене, и вычисляем простые логарифмические уравнения Оба корня принадлежат ОДЗ, по условию найдем их сумму: x₁+x₂=0,5+8=8,5. Ответ: 8,5 – Д.

С простых примеров на раскрытие логарифмических уравнений Вы увидели, что достаточно знать несколько формул и базовые свойства логарифма и уже можно самостоятельно решать уравнения. Для простых условий это работает, но напоминаем, что курс ВНО подготовки содержит 40 примеров, причем ряд задач сочетают в себе не только логарифмы, но и корни, модули, показательные выражения. Вы научитесь сводить уравнения к квадратным, логарифмировать и еще много чего нового.

Как посчитать логарифм

Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма \(log_{a}(b)\) существует только при положительных значениях основания \(a\) и аргумента \(b\). И кроме этого на основание накладывается условие, что оно не должно быть равно \(1\).

Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).

При этих ограничениях логарифм существует.

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д. Так как (вспоминайте определение отрицательной степени)

Так как (вспоминайте определение отрицательной степени)

Теперь давайте разберем общий алгоритм вычисления логарифмов:

• Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
• Разобраться в какую степень \(x\) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
• \(x\) и будет искомым значением логарифма.

Давайте разберем на примерах.

Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_{3}(9)\)

• Сначала представим аргумент и основание в виде степени тройки:
  $$ 3=3^1, \qquad 9=3^2;$$
• Теперь надо разобраться в какую степень \(x\) нужно возвести \(3^1\), чтобы получить \(3^2\)
  $$ (3^1)^x=3^2, $$
  $$ 3^{1*x}=3^2, $$
  $$ 1*x=2,$$
  $$ x=2.$$
• Вот мы и решили:
  $$log_{3}(9)=2.$$

Пример 2. Вычислить логарифм \(\frac{1}{125}\) по основанию \(5\): \(log_{5}(\frac{1}{125})\)

• Представим аргумент и основание в виде степени пятерки:
  $$ 5=5^1, \qquad \frac{1}{125}=\frac{1}{5^3}=5^{-3};$$
• В какую степень \(x\) надо возвести \(5^1\), чтобы получить \(5^{-3}\):
  $$ (5^1)^x=5^{-3}, $$
  $$ 5^{1*x}=5^{-3},$$
  $$1*x=-3,$$
  $$x=-3.$$
• Получили ответ:
  $$ log_{5}(\frac{1}{125})=-3.$$

Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_{64}(4)\)

• Представим аргумент и основание в виде степени двойки:
  $$ 64=2^6, \qquad 4=2^2;$$
• В какую степень \(x\) надо возвести \(2^6\), чтобы получить \(2^{2}\):
  $$ (2^6)^x=2^{2}, $$
  $$ 2^{6*x}=2^{2},$$
  $$6*x=2,$$
  $$x=\frac{2}{6}=\frac{1}{3}.$$
• Получили ответ:
  $$ log_{64}(4)=\frac{1}{3}.$$

Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_{8}(1)\)

• Представим аргумент и основание в виде степени двойки:
  $$ 8=2^3 \qquad 1=2^0;$$
• В какую степень \(x\) надо возвести \(2^3\), чтобы получить \(2^{0}\):
  $$ (2^3)^x=2^{0}, $$
  $$ 2^{3*x}=2^{0},$$
  $$3*x=0,$$
  $$x=\frac{0}{3}=0.$$
• Получили ответ:
  $$ log_{8}(1)=0.$$

Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_{5}(15)\)

Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 \qquad 15= ???;$$
\(15\) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$

Внимание!

Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.

\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.

Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.

Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.

Решение логарифмических неравенств, содержащих переменную в основании логарифма: методы, приемы, равносильные переходы

Рассмотрим стандартные логарифмические неравенства, содержащие переменную в основании логарифма.

Способы решения этих неравенств:

• рассматривают два случая: основание больше единицы и основание положительно и меньше единицы и решают совокупность двух систем;
• используют обобщенный метод интервалов, заключающийся в приведении неравенства к виду $$ h(x) = \log _{g \left( x \right)} f\left( x \right) \vee 0 $$ (где символом обозначен один из знаков $$< ,\quad > ,\quad \le ,\quad \ge $$), разбиении D(h) нулями h(x) на несколько интервалов и определении знака h(x) на каждом интервале по ее знаку в одной из точек соответствующего интервала.
• используют метод, основанный на замене функций. Напомним, что если область определения, нули и промежутки знакопостоянства функции h(x) соответственно совпадают с областью определения, нулями и промежутками знакопостоянства функции g(x), то неравенства p(x)h(x) $$ \vee$$ 0 и p(x)g(x) $$ \vee$$ 0 равносильны.

1. Неравенство вида $$ \log _{g \left( x \right)} f\left( x \right) \vee 0 $$

Решение: Решением неравенства $$ \log _{g \left( x \right)} f\left( x \right) \vee 0 $$ будет решение равносильной системы $$ \left\{ \begin{array}{l} \left( {f\left( x \right) — 1} \right)\left( {g\left( x \right) — 1} \right) > 0; \\ f\left( x \right) > 0; \\ g\left( x \right) > 0; \\ g\left( x \right) \ne 1. \\ \end{array} \right. $$

2. Неравенство вида $$ \log _{g(x)} f(x) \vee b $$

Решение: Решением неравенства $$ \log _{g(x)} f(x) \vee b $$ будет решение равносильной системы $$ \left\{ \begin{array}{l} \left( {f(x) — g^b (x)} \right)\left( {g(x) — 1} \right) \vee 0 \\ f(x) > 0; \\ g(x) > 0; \\ g(x) \ne 1. \\ \end{array} \right. $$

3. Неравенство вида $$ log_{h(x)} f(x) \vee \log _{h(x)} g(x) $$

Решение: Решением неравенства $$ log_{h(x)} f(x) \vee \log _{h(x)} g(x) $$ будет решение равносильной системы $$ \left\{ \begin{array}{l} \left( {f(x) — g(x)} \right)\left( {h(x) — 1} \right) \vee 0 \\ f(x) > 0; \\ g(x) > 0; \\ h(x) > 0; \\ h(x) \ne 1. \\ \end{array} \right. $$

4. Неравенство вида $$ \log _{f(x)} h(x) \vee \log _{g(x)} h(x)$$

Решение: Решением неравенства $$ \log _{f(x)} h(x) \vee \log _{g(x)} h(x)$$ будет решение равносильной системы $$ \left\{ \begin{array}{l} \left( {h(x) — 1} \right)\left( {g(x) — f(x)} \right)\left( {f(x) — 1} \right)\left( {g(x) — 1} \right) \vee 0 \\ f(x) > 0; \\ g(x) > 0; \\ h(x) > 0; \\ g(x) \ne 1; \\ f(x) \ne 1. \\ \end{array} \right.$$

5. Неравенство вида $$ \log _{\varphi \left( x \right)} f\left( x \right) \cdot \log _{h\left( x \right)} g\left( x \right) < 0$$

Решение: Решением неравенства $$ \log _{\varphi \left( x \right)} f\left( x \right) \cdot \log _{h\left( x \right)} g\left( x \right) < 0$$ будет решение равносильной системы $$ \left\{ \begin{array}{l} \left( {f\left( x \right) — 1} \right)\left( {\varphi \left( x \right) — 1} \right)\left( {g\left( x \right) — 1} \right)\left( {h\left( x \right) — 1} \right) \vee 0; \\ f\left( x \right) > 0; \\ \varphi \left( x \right) > 0; \\ \varphi \left( x \right) \ne 1; \\ g\left( x \right) > 0; \\ h\left( x \right) > 0; \\ h\left( x \right) \ne 1. \\ \end{array} \right.$$

Решение логарифмических уравнений через преобразование

Редкий раз решение логарифмических уравнений обходится без проведения преобразований. Характерными для логарифмических уравнений являются преобразования, проводящиеся на базе свойств корней и степеней. Все они по отдельности разобраны в статье «Преобразование логарифмических уравнений». Здесь мы рассмотрим примеры решения логарифмических уравнений со сравнительно сложными последовательностями преобразований.

Для начала напомним о необходимости использования модулей при вынесении четных показателей степеней из-под знаков логарифмов, а также при переходе от логарифмов произведений (частных) к суммам (разностям) логарифмов.

Пример. Про модуль не забыть.

Решите логарифмическое уравнение

Решение

Просматривается возможность прийти к одинаковым логарифмам в левой части уравнения. Для начала вынесем показатель 2 из-под знака логарифма, и так как он есть четное число, то не забудем про модуль:

Для раскрытия модуля нам потребуется ОДЗ для исходного уравнения:

С учетом этого, имеем

Дальше все просто:

Ответ:

−2

Теперь еще раз обратим внимание на преобразование квадратов, кубов и других степеней логарифмов. Уж очень часто приходится видеть неверные преобразования, типа , вместо , или , вместо и т.п.. Пример

Квадраты логарифмов.

Пример. Квадраты логарифмов.

Решите уравнение

Решение

Просматривается возможность упростить вид заданного логарифмического уравнения. Для начала перепишем его как , чтобы не наделать ошибок при преобразовании квадратов логарифмов. Дальше все довольно прозрачно:

Теперь пора ввести новую переменную:

Остается вернуться к старой переменной:

Ответ:

3; 9

Наконец, рассмотрим пример решения довольно сложного логарифмического уравнения, где сильно переплетены степени и логарифмы.

Пример

Решите уравнение

Решение

Просматриваются черты основного логарифмического тождества. Сейчас поработаем в этом направлении. Но сначала давайте найдем область допустимых значений переменной x – она бывает нужна при проведении преобразований и при проведении проверки. Тем более, в нашем случае ОДЗ находится легко:

Теперь приступаем к преобразованию:

А дальше все легко:

При найденных значениях переменной знаменатели дробей в уравнении в нуль не обращаются, а также и 2 принадлежат ОДЗ для исходного уравнения, следовательно, являются его корнями.

Ответ:

; 2

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x 4 к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Свойства логарифмов

Логарифмы, как и числа, можно складывать, умножать и делать множество действий с ними. Как не запутаться в них, не производить лишних вычислений и не ошибиться? Для этого нужно хорошо знать все свойства, которые представлены в таблице ниже. Каждое из рассмотренных в таблице свойств можно использовать для преобразований.

Рассмотрим каждое свойство чуть подробнее. 

Свойство 1. \(log_ab^m=m*log_ab\). 

Попробуем найти значение выражения \(log_28^2\) без применения свойства. Тогда возведем аргумент в степень и получим:

\(log_28^2=log_264\)

Воспользовавшись определение логарифма, заметим, что \(log_264=6\).Но что делать, если числа окажутся большими, или, более того, у логарифма не будет точного значения — примером такого логарифма может служить \(log_57\). Да и вычисление в несколько действий с большими числами может занять много времени. 

Именно поэтому мы применяем это свойство! 

\(log_28^2=2*log_28=2*3=6\)

Свойство 2. \(log_{a^n}b=\frac{1}{n}*log_ab\)

Рассмотрим на примере логарифма \(log_{2^2}4\). Посчитаем без свойства:

\(log_{2^2}4=log_44=1\)

Заметим, что:

• в первом свойстве мы увеличивали аргумент логарифма (то есть конечный результат, который получается при возведении числа в степень);
• в этот раз мы увеличиваем уже число, которое возводим в степень. 

Сравните:

\(2^2=4\) или \(3^2=9\)

Следовательно, когда мы будем производить «обратные» действия, то есть считать логарифм, то при увеличении основания степени (и сохранении результата возведения в степень), у нас должна уменьшиться сама степень, в которую мы возводим. 

Например:

\(2^4=16\) и \(4^2=16\)

Именно поэтому у нас появляется дробь: она уменьшает степень во столько раз, во сколько мы увеличили первоначальное число:

\(log_{2^2}4=\frac{1}{2}log_24=\frac{1}{2}*2=1\)

Свойство 3. \(log_{a^n}b^m=\frac{m}{n}*log_ab\)

Это свойство вытекает из двух предыдущих, просто их соединили вместе. Иначе пришлось бы отдельно выносить степень из аргумента и отдельно из основания логарифма. Сравните:

\(log_{2^3}5^7=7*log_{2^3}5=7*\frac{1}{3}*log_25=\frac{7}{3}log_25\)или\(log_{2^3}5^7=\frac{7}{3}log_25\)

Свойство 4. \(log_ab+log_ac=log_a(b*c)\)

Найдем значение выражения \(log_24+log_28\):

\(log_24+log_28=2+3=5\)

Но в случае, когда числа не будут так легко считаться (или вовсе не будут считаться), на помощь придет это свойство:

\(log_512,5+log_52=log_525=2\)

Свойство 5. \(log_ab-log_ac=log_a\frac{b}{c}\)

Аналогично с предыдущим свойством это нужно для упрощения вычислений. 

Например:

\(log_318-log_32=log_3\frac{18}{2}=log_39=2\)

Свойства 6 и 7. \(log_aa=1\) и \(log_a1=0\)

Эти свойства напрямую связаны с возведением числа в степень. Достаточно лишь ответить на два вопроса:

• В какую степень нужно возвести число, чтобы получилось такое же число?
• В какую степень нужно возвести любое число, чтобы получить 1?

Ответы на эти вопросы будут 1 и 0. Отсюда и эти свойства:

• Число в степени 1 будет равно само себе: \(log_aa=1\).
• Число в степени 0 будет равно 1: \(log_a1=0\).

Свойство 8. \(log_ab=\frac{log_cb}{log_ca}\)

Это свойство используется в случаях, когда нам нужно представить логарифм с любым другим основанием. 

Например:

\(log_25=\frac{log_35}{log_25}\)

Это свойство может пригодиться в решении уравнений и неравенств для упрощения выражений. 

Свойство 9. \(log_ab=\frac{1}{log_ba}\)

Что делать, если нам нужно представить логарифм с определенным основанием, которое равно аргументу этого логарифма? Все просто: мы можем поменять основание и аргумент местами, если воспользуемся свойством \(log_ab=\frac{1}{log_ba}\).

Например:

\(log_{27}3=\frac{1}{log_327}=\frac{1}{3}\)

Заметим, что это же выражение можно было решить немного по-другому:

\(log_{27}3=log_{3^3}3=\frac{1}{3}*log_33=\frac{1}{3}\).

В этом случае мы воспользовались свойствами 2 и 6.

Свойство 10. \(a^{log_cb}=b^{log_ca}\)

Еще одно свойство, которое позволяет изменить аргумент логарифма, и при этом не менять значение выражения. 

Рассмотрим на примере \(2^{log_24}\):

 \(2^{log_24}=2^2=4\)\(2^{log_24}=4^{log_22}=4^1=4\)

Для более простого запоминания свойств логарифмов предлагаем вам воспользоваться нашими забавными ассоциациями.  

Теперь, когда мы знаем свойства логарифмов, мы можем перейти к более сложным преобразованиям — к решениям уравнений и неравенств.

Простейшие логарифмические уравнения

В других статьях мы уже рассматривали разные виды уравнений: линейные, квадратные, показательные и т.п. Настало время узнать про логарифмические уравнения. 

Логарифмическое уравнение — это уравнение, в котором неизвестная стоит в аргументе или основании логарифмов. 

Иными словами, если в уравнении мы видим логарифм с неизвестной — это логарифмическое уравнение. 

Например, \(log_2x=4\) — логарифмическое уравнение. 

А вот \(log_25+x=x^2\) не будет логарифмическим уравнением, поскольку неизвестная не стоит ни в аргументе, ни в основании логарифма. 

Как решать логарифмические уравнения?Логарифмическое уравнение нужно привести к такому виду:

\(log_af(x)=log_ag(x)\).

При решении таких уравнений нужно обязательно учитывать, что по определению аргумент логарифма всегда должен быть больше нуля, а основание больше нуля и не должно равняться единице. Эти ограничения называются областью допустимых значений или ОДЗ логарифма. 

Область допустимых значений — это те значения, которые может принимать переменная x (или другая буква латинского алфавита) в выражении.

\(log_ab\)ОДЗ логарифма: a > 0, a ≠ 0, b> 0.

Как быстро избавиться от логарифмов с одинаковым основанием?Это можно сделать, приравняв аргументы. Почему мы можем так сделать? Представим, что мы возводим некоторое число в степень, это число будет стоять в основании логарифма. Если два логарифма равны, то и степени, в которые мы возвели число, равны. Следовательно, будет равен и результат возведения в степень, то есть аргумент логарифма!\(a^x=b\)\(log_ab=x\)Тогда пусть \(log_ab=log_ac\)\(x=log_ac\)\(a^x=c => b=c\)При этом проверить ОДЗ можно только у одного из логарифмов, поскольку если один из них положителен, а второй равен первому, то и второй будет положительным.Например, если b=2, то из равенства b=c получаем c=b=2.В логарифмических уравнениях встречаются более сложные выражения, которые в дальнейшем мы будем выражать в виде функций — например, f(x) или g(x).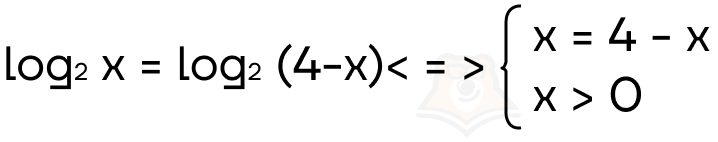Например:

Алгоритм решения логарифмического уравнения:1. Написать ОДЗ.2. Упростить выражения слева и справа от знака равенства, используя свойства логарифмов, если это возможно.3. Если основания логарифмов одинаковые, избавиться от логарифмов. В противном случае — используя свойства логарифмов, привести к одинаковому основанию, а уже потом совершить эти действия.4. Решить уравнение и сравнить с ОДЗ, выписать в ответ корни.

Рассмотрим на примере:

\(log_2(5x-4)=log_2(x+8)\)

1. В первую очередь найдем ОДЗ. Для этого вспомним, что аргумент логарифма всегда строго положителен:

\(5x-4>0\) и \(x+8>0\)

Найдем возможные значения х:

\(5x>4\) и \(x>-8\)\(x>\frac{4}{5}\) и \(x>-8\)

Нанесем найденные промежутки на числовую прямую и определим, какие значения может принимать х. Для этого нам нужно будет найти промежутки, которые удовлетворяют обоим неравенствам: 

Теперь мы можем определить ОДЗ: \(x \in(\frac{4}{5};+{\infty})\)

2. Если в обеих частях уравнения находится логарифм по одинаковому основанию, то можно «скинуть» логарифмы и записать равенство аргументов. Поскольку и у первого, и у второго логарифма основания равны 2, то мы можем приравнять их аргументы: 

\(5x-4=x+8\)

3. Решим полученное уравнение:

\(5x-x=8+4\)\(4x=12\)\(x=3\)

4. Подставим в ОДЗ и проверим, подходит ли корень. Поскольку \(3>\frac{4}{5}\), то корень нам подходит. 

Ответ: 3.

А теперь немного усложним задачу. Допустим, переменная будет стоять и в основании, и в аргументе логарифма. 

Рассмотрим еще одно уравнение: 

\(log_2(x-4)=log_{4x}4+log_{4x}x\)

1. Найдем ОДЗ. Аргумент логарифма всегда строго больше 0, а основание больше 0 и не равно 1. Тогда получаем следующие неравенства для аргументов логарифмов:

\(x>0\)\(x-4>0\)

И для оснований логарифмов:

\(4x>0\)\(4x\neq1\)

Решим неравенства:

\(x>0\)\(x>4\)\(x>0\)\(x\neq\frac{1}{4}\)

Теперь отметим все ограничения на числовой прямой и найдем, чему равна ОДЗ:

Поскольку нам нужно, чтобы ограничение удовлетворяло всем полученным неравенствам и уравнениям, то \(x\in(4;+{\infty})\).

2. Теперь перейдем к решению самого уравнения. По свойствам логарифма (свойства 4 и 6) преобразуем правую часть уравнения:

\(log_2(x-4)=log_{4x}4x\)\(log_2(x-4)=1\)

3. Чтобы отбросить логарифмы и перейти к уравнению с аргументами, необходимо, чтобы их основания были равны. Поскольку основание левого логарифма равно 2, то представим правую часть в виде логарифма с таким же основанием 2:

\(log_2(x-4)=log_22\)

4. Отбросим логарифмы и перейдем к уравнению с ними:

\(x-4=2\)\(x=6\)

Поскольку \(6>4\), то корень принадлежит ОДЗ, а значит, его можно записать в ответ. 

Ответ: 6.

Мы разобрали уравнения с логарифмами. Остался вопрос: а как решать неравенства с ними? 

Учет области определения

Теперь поговорим об области определения логарифмической функции, а также о том, как это влияет на решение логарифмических уравнений. Рассмотрим конструкцию вида

Такое выражение называется простейшим — в нем лишь одна функция, а числа а и — это именно числа, а ни в коем случае не функция, зависящая от переменной х. Решается оно очень просто. Достаточно лишь использовать формулу:

Данная формула является одним из ключевых свойств логарифма, и при подстановке в наше исходное выражение мы получим следующее:

Далее, поскольку и слева, и справа стоит логарифмы по одному и тому же основанию, мы избавляемся от них:

Это уже знакомая формула из школьных учебников. У многих учеников наверняка возникнет вопрос: поскольку в исходном выражении функция () стоит под знаком log, на нее накладываются следующие ограничения:

(х) > 0

Это ограничение действует потому, что логарифм от отрицательных чисел не существует. Так, может быть, вследствие этого ограничения следует ввести проверку на ответы? Быть может, их нужно подставлять в исходник?

Нет, в простейших логарифмических уравнениях дополнительная проверка излишня. И вот почему. Взгляните на нашу итоговую формулу:

Дело в том, что число а в любом случае больше 0 — это требование тоже накладывается логарифмом. Число а является основанием. При этом на число никаких ограничений не накладывается

Но это и неважно, потому что в какую бы степень мы бы не возводили положительное число, на выходе мы все равно получим положительное число. Таким образом, требование (х) > 0 выполняется автоматически

Что действительно стоит проверять, так это область определения функции, стоящей под знаком log. Там могут встречаться довольно непростые конструкции, и в процессе решения за ними обязательно нужно следить. Давайте посмотрим.

Первый шаг: преобразуем дробь справа. Получим:

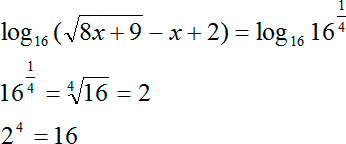
Избавляемся от знака логарифма и получаем обычное иррациональное уравнение:

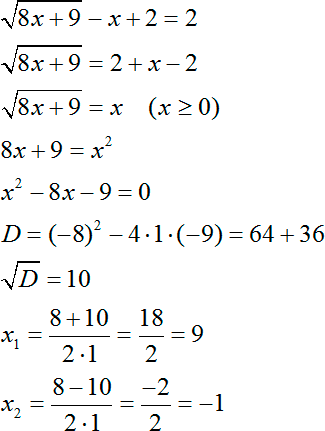
Из полученных корней нас устраивает только первый, так как второй корень меньше нуля. Единственным ответом будет число 9. Все, задача решена. Никаких дополнительных проверок того, что выражение под знаком логарифма больше 0, не требуется, потому что оно не просто больше 0, а по условию уравнения оно равно 2. Следовательно, требование «больше нуля», выполняется автоматически.

Здесь все то же самое. Переписываем конструкцию, заменяя тройку:

Избавляемся от знаков логарифма и получаем иррациональное уравнение:

Возводим обе части в квадрат с учетом ограничений и получаем:

х + 4 ≥ 0

Решаем полученное уравнение через дискриминант:

Но = −6 нас не устраивает, потому что если мы подставим это число в наше неравенство, то получим:

В нашем же случае требуется, чтобы было больше, чем 0 или в крайнем случае равно. А вот = −1 нам подходит:

Единственным ответом в нашем случае будет = −1. Вот и все решение. Давайте вернемся в самое начало наших вычислений.

Основной вывод из этого урока: проверять ограничения для функции в простейших логарифмических уравнениях не требуется. Потому что в процессе решения все ограничения выполняются автоматически.

Однако это ни в коем случае не означает, что о проверке можно вообще забыть. В процессе работы над логарифмическим уравнением вполне может перейти в иррациональное, в котором будут свои ограничения и требования к правой части, в чем мы сегодня и убедились на двух различных примерах.

Смело решайте такие задачи и будьте особо внимательные, если в аргументе стоит корень.

Как считать логарифмы в Python

Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:

И теперь посчитаем log₂ 8, используя метод math.log (b, a):

Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание

Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.

Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:

Для подсчёта десятичного и двоичного логарифма есть отдельные методы:

Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:

Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:

Это все основные инструменты для работы с логарифмами в Python.